热脉冲法瞬态测量材料热物性研究
向泽英 罗 浩 陈昭栋 陈 丕 陈 芬
(1. 西南科技大学理学院 四川绵阳 621010; 2. 西南应用磁学研究所 四川绵阳 621000)
20世纪90年代,热脉冲法由斯洛伐克科学家Kubicar提出,经过不断完善,广泛应用于科学研究、工业生产等领域。于帆等[1]通过对NIST纤维板标准材料和聚四氟乙烯塑料试样的测试发现,在满足理想模型条件下,测量误差±5%;朱苏康等[2]对有机玻璃和非织造布试样的热物性分别进行了测量,结果表明热脉冲法可以同时测量非织造布的热导率、热扩散系数及体积热容3个热物性参数;戴景民等[3]对传统热脉冲法进行改进,提出了一种适用于防隔热材料高温高精度热物性测量的保护平面热源法,测量误差低于6%,并进行标定实验研究。
热脉冲法作为一种经典的热物性测量技术,具有测量范围广、时间短且可以同时测出多个热物性参量的优点。
针对一维半无限大传热数学模型,本文通过热脉冲加热停止后热面的降温规律对其间接求解。同时,应用信号采集、处理等高新技术,在理论、技术方面做了进一步改进和提高,研制出SHT-P热脉冲法热物性瞬态自动测量仪,并对聚脂玻璃钢和老化聚氨脂泡沫试样进行测试,测量精度高、测试范围广。
1 热脉冲法测量原理
热脉冲法在输入瞬态脉冲热干扰信号后,通过测量试样内某一点温度响应信号就可以同时得到热导率、热扩散系数、体积热容等热物性参数。热脉冲法所依据的原理是一维半无限大传热数学模型,以此作为理论基础,建立一类热物性的测量方法是可行的[4-5]。
1.1 一维半无限大传热模型的定解问题
一维半无限大传热模型的定解问题可以表示为[6]:
(1)
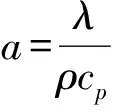
通过拉氏变换求解(1)式,解得其精确解为[6]:
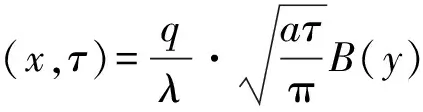
(2)
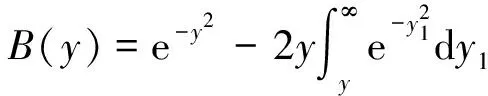
(3)
y2=x2/(4aτ)
(4)
式(2)中,函数B(y)为含定积分的超越方程,对求解带来很大困难。那么,如果找出脉冲加热停止后热面的降温规律,同样可以解决此问题,这也是热脉冲法的真正含义。
1.2 脉冲加热停止后热面的降温规律
脉冲加热到t1时刻,停止加热,至t2i时刻。根据热传导理论[7],热面会向低温方向传热,导致热面温度降低,冷面的温度升高。热面的温度降低的过程用托哈美尔定理证明,得:
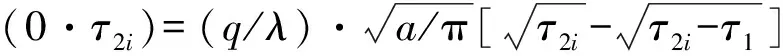
(5)
式(5)表达了脉冲加热停止之后,热面降温随时间变化的关系。联立式(2)、式(5)得:
(6)
式(6)右端的温变和时间参量在实验中可以直接测量,因此,计算得到函数Bi(y)后,根据式(3)解出yi,从而,实现对热扩散系数ai等热物性参量的测量。
2 SHT-P热物性瞬态自动测量仪
2.1 热脉冲法瞬态测量材料热物性
实验仪器采用西南科技大学理学院自主研发的SHT-P热物性瞬态自动测量仪(参数网络可查)。测量仪从τ=0开始加热,到τ1时刻停止加热的这一脉冲加热时间段中,τ1和ϑ(x,τ1)由测量获得。在脉冲加热停止之后继续进行测量,可获得τ2i和ϑ(0,τ2i)。当数据量达70组时,测量结束。这样,顺序选择i=1,2,3……n个τ2i以及相对应ϑ(0,τ2i)作为一个样本。根据测量得到的τ1和ϑ(x,τ1),可用式(6)计算出n个Bi(y)的数值。利用上述计算获得的Bi(y)的数值,由式(3)反解求出yi的值[8]。
计算热扩散系数:将yi代入式(4),得
(7)
计算热导率:用测量值I,R,A,ai,ϑ(0,t2i),t2i等,代入式(5),得
(8)
探求热导率、热扩散系数的经验公式。ai,λi对应的温度,当i取n-1和n时,对应的温度可以从测量列表中查出,设为Ti=n-1和Ti=n,可以认为ai,λi对应的温度可以用其中值温度来表征[9]。即
(9)
这样,就可以建立数据库。引用前面计算获得的热导率和热扩散系数及用式(9)得到的温度Ti即可构建数据库:[ai,λi,Ti]。以这个数据库为依据,可以找出在测量涉及的温度范围内,热导率和热扩散系数的经验公式。经验公式的具体寻找方法,是用最小二乘法作二次曲线拟合。计算热导率、热扩散系数在室温附近温度测量范围内的经验公式为[10-11]
λ(T)=η0+η1T+η2T2[T1,T2]
(10)
(11)
作为一次特定测量的结果,也可以计算拟合中值温度时的热导率、热扩散系数,拟合中值温度,用式(12)取整得到。
(12)
用式(12)代入式(10)、式(11),分别算出λ(T),a(T),这里的热导率、热扩散系数也是这次特定测量的结果。在测量温度范围内的经验公式和测量中值温度下的λ(T),a(T)的数值,都将视为热脉冲法瞬态测量获得的热导率和热扩散系数的测量结果。
2.2 一维半无限大传热模型的布置
根据一维半无限大传热模型,待测试件应具有如下特征:由长宽均为200 mm的主试件、辅试件1和辅试件2三块同一材料平板组成,主试件的厚度x可以在4~20 mm间取值,辅试件1厚度D≥3xmm, 辅试件2的厚度d≥2xmm。
3块试件叠放时,接触面应光洁平整,热接触良好,如图1所示。
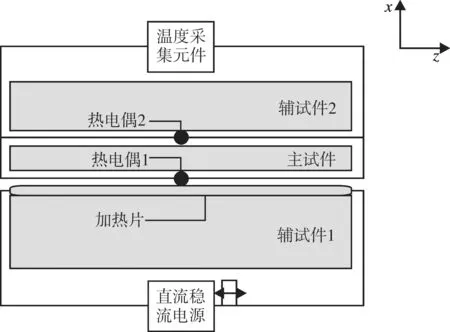
图1 待测试件的布置示意图Fig. 1 Layout of the test piece
辅试件1置于底部,平面热源处于主试件与辅试件1之间,且有效发热面与主试件重合;主试件与平面热源上表面之间安置温差电偶1,测温点位于主试件下表面中央,用于测量热面的温度变化;主试件与辅件2之间安置温差电偶2,测温点位于主试件上表面中央,用于测量冷面的温度变化。这种对称布置,只要在规定时间内加热,热流强度就不会传出辅试件1的下表面和辅试件2的上表面。那么,在X轴的正方向,就可以认为实现了半无限大的一维传热。
2.3 仪器结构
SHT-P热物性瞬态自动测量仪由直流稳流电源、加热测量装置、测温元件、温度采集模块、中央处理器、数据处理系统6个部分组成,具体结构如图2所示。
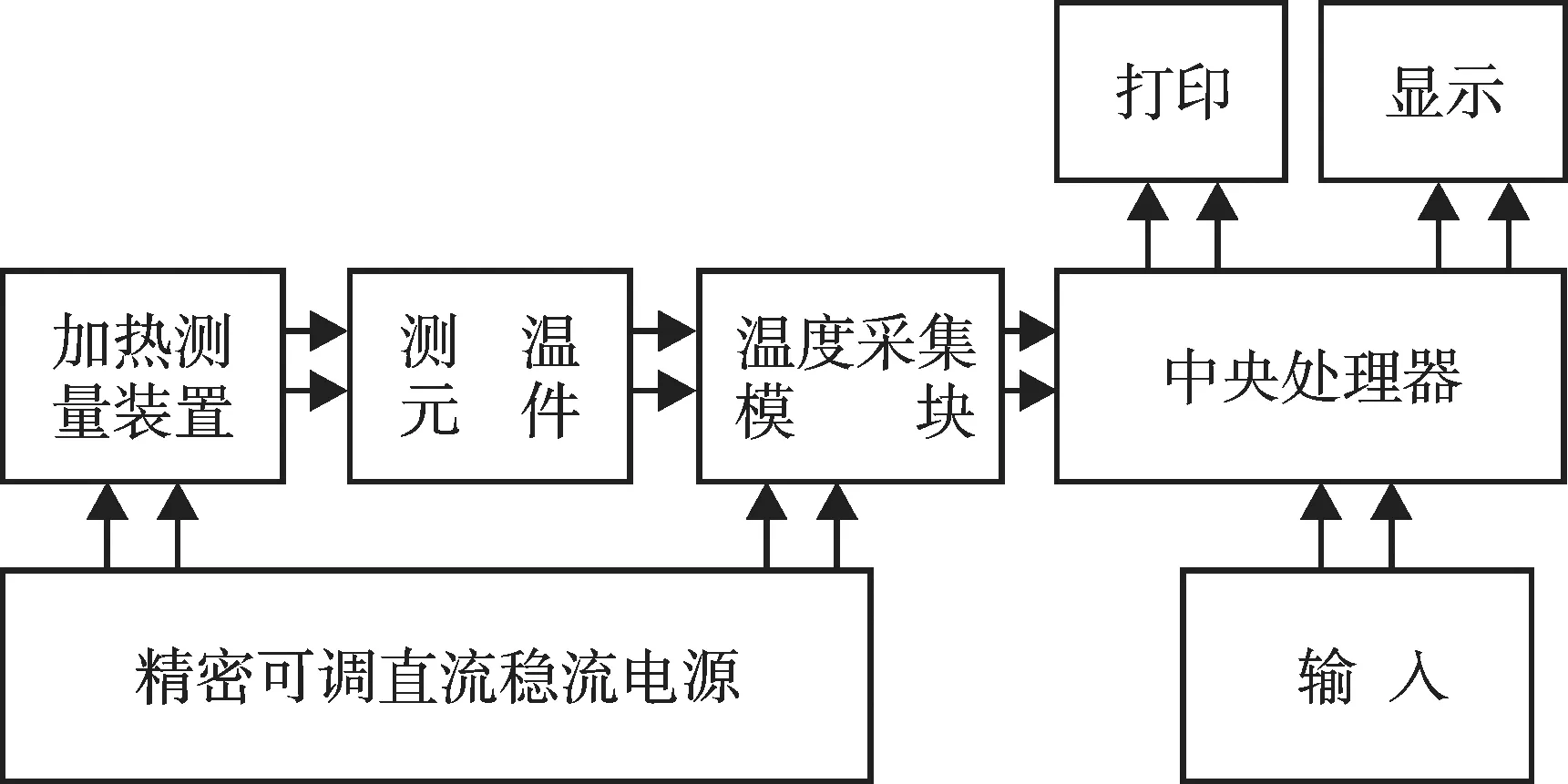
图2 SHT-P热物性瞬态自动测量仪结构图Fig.2 Structure of SHT-P transient automatic measuring instrument of thermo-physical properties
本系统以中央处理器为控制核心,通过调节直流稳流电源加热测量装置提供所需的脉冲平面热源;测温元件为加热装置反馈温度信息;温度采集模块以一定频率采集热脉冲信号,经数据处理系统计算出热物性参量。
3 实验结果及分析
3.1 实验测量
本文利用热脉冲瞬态自动测量仪分别对聚脂玻璃钢和老化聚氨脂泡沫进行测量,室温下热物性测量结果如表1所示。

表1 室温下SHT-P对聚脂玻璃钢和老化聚氨脂泡沫的测量数据Table 1 Measurement data of GFRP and aged polyurethane foam by SHT-P at room temperature
由表1可知,老化聚氨脂泡沫热导率λ=0.033 6 W·m-1·K-1,与中国测试技术研究院的防护热板法测量值λ0=0.032 8 W·m-1·K-1相对误差为2.4%,在中国测试技术研究院规定的使用仪器误差范围内。
为了进一步验证该方法的重复性,又对干燥松木板在同等条件下进行了多次测量,测量数据如表2。可知,热脉冲法测量材料热物性稳定性很好。
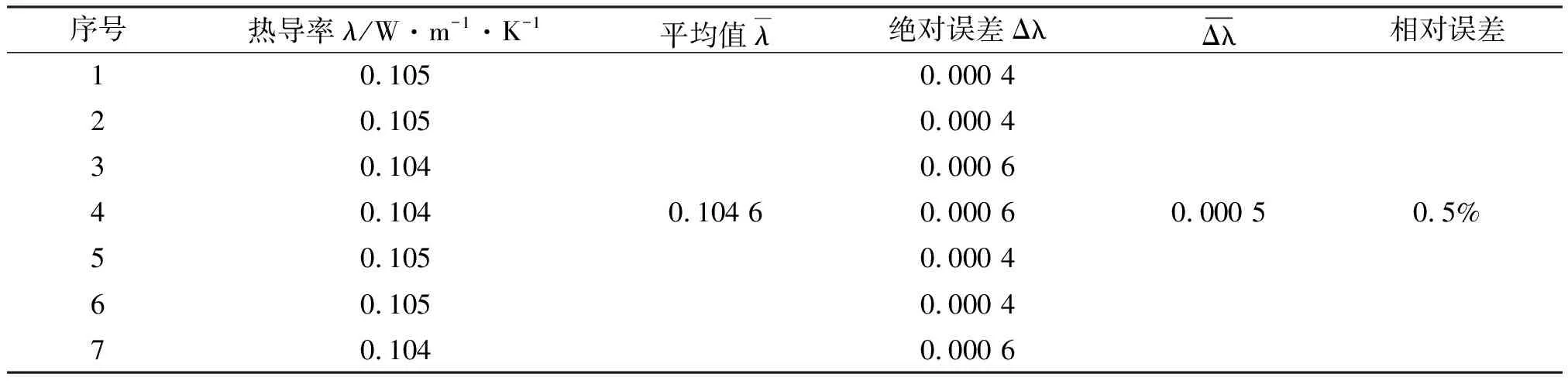
表2 同一样品(松木板)在同等条件下多次测量热导率数据Table 2 Measurement of thermal conductivity data of the same sample (pine wood) for multiple times under the same conditions
3.2 测量仪的可靠性分析
测量仪的测量误差,随机部分在数据处理中做估算。这里,仅对仪器设计中涉及到的一些会引起误差的因素进行分析,用以考察测量仪的可靠性。
首先,加热片用于加热待测材料,以便在加热中和停止加热后测量材料的温度变化规律,实现对热物性的测量。由于加热片并非理想的平面热源,它是由导体材料和保护涂层构成,有一定的质量和厚度。实际使用的加热片,有效加热面积为0.04 m2,质量m0≈0.016 4 kg,其定压比热主要由导电材料和保护涂层决定,为cp0≈460 J·kg-1·K-1;加热片的最大发热功率约为80 W/m2[12]。
实际测量中,加热测量时间一般在200 s之内,加热电流选0.7 A左右。发热元件的电阻约为36 Ω。温升取20 ℃估算。根据这些数据,可以估计加热片自身吸热带来的误差。测量中,介质的平均升温速度[13]为:
由于采用稳流电源供电,加热片的发热功率几乎是稳定不变的,可以估算为:
W0=I2R=0.72×36=17.64 W
这些能量主要用于向介质传递,使之温度升高。自然,还有少量的能量,将用于提高加热片自身的温度。不难计算出,这部分能量对介质温升没有贡献,应该予以扣除[14],这部分能量可以估算为[8]:
因而,可以估算出加热片自身吸热功率占发热功率的比例为:
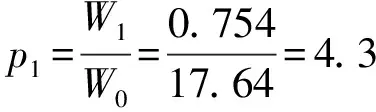
这是最大的一项误差来源,显然是不可忽略的,应当加以修正。
此外,加热电流的测不准量略为1 mA。其不准量占发热功率的比为:
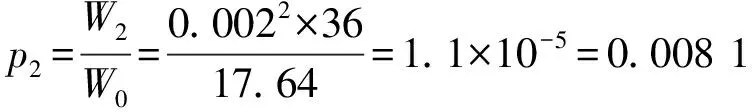
这是比较小的,可以略而不计。
电阻测量的不准确量约为0.01 Ω。由此引起误差约为:
这是比较小的,也可以略去。
综上所述,除加热片自身吸热的影响之外,其他因素引起的误差总和不会超出0.2%。在要求不是特别精密的情况,这些误差是可以接受的。
加热片自身吸热造成的测量误差是必需修正的。由于我们从测量数据中可以得到任何记数时间点的升温速度Δϑ/Δτ,可以修正加热片自身吸热的影响,同时认为加热片的吸热功率是减小了界面的热流强度,因此,其有效加热热流强度应该为[6]:
(13)
作此修正后,样机的测量误差可以大为减少。
测量仪按(13)式对加热片自身吸热进行了修正,消除了这一影响。可以预期,测量的可靠性会得到改进,测量结果更加可靠。
4 结论
(1)本文根据热脉冲加热结束后热面降温的曲线规律,进而求解一维半无限大传热模型,计算更简便,结果更精确。(2)在室温下,测试聚脂玻璃钢和老化聚氨脂泡沫结果表明:相对误差2.4%,测量时间5 min左右,可以一次性测得热导率、热扩散系数、比热等多个热物理参量。(3)本文测量环境温度为20~100 ℃,对于高温环境下材料热物性测量,有待进一步探究。(4)热物性瞬态测量仪不要求恒温环境,不必达到苛刻的热平衡状态,简化了仪器的结构,极大提高了测量速度,容易实现自动化和数字化,也有效地提高了热物性测量的准确性。理论分析、仪器研制和实际测量都证明热脉冲法是科学的和切实可行的,值得推广和运用,可以期望成为热物性测量的一个优先发展方向。

