某特种车非圆齿轮无级变速器锥形离合器动力学仿真分析
赵重年1 杨聪2 李红勋3
1.陆军军事交通学院学员五大队研究生队 天津 300161
2.汉阳专用汽车研究所 湖北武汉 430056
2.陆军军事交通学院军事交通运输研究所 天津 300161
1 前言
现广泛应用于民用汽车的无级变速器(C V T,Continuously Variable Transmission)以摩擦式无级变速为主,但其在性能上存在难以克服的缺陷,易打滑、易损坏、传动比范围小、特别是转矩容量低,钢带寿命短,故很难满足大负荷的传动要求。针对以上问题,某特种车拟采用三分支非圆齿轮无级变速器取代传统的摩擦式无级变速器,其结构如图1所示。
2 传动原理
2.1 非圆齿轮无级变速原理
非圆齿轮无级变速器的动力分两路输入至第一、二非圆主动齿轮,在凸轮机构与锥形离合器的协调控制下,从第一、二非圆从动输出至差速机构的太阳轮与行星架,最终由差速机构的齿圈以定传动比输出,当改变两非圆主动齿轮的相位时,非圆齿轮输出传动比随之改变,经过差速机构输出的定传动比也随之改变,由于相位的变化是连续的,差速机构输出传动比也就是连续的,即无级变速。

图1 非圆齿轮无级变速器结构
设图1(b)中非圆齿轮无级变速机构的输入转速为nin,输出转速为nout,第一非圆齿轮对1/2的主、从动轮瞬时节曲线极径分别为R2、 R1,第二非圆齿轮对9/10的主、从动轮瞬时节曲线极径分别为R9、 R10, 差速机构太阳轮转速为nS、行星 架 转 速 为nH、 齿 圈 转 速 为nR, 则n2= n9= nin, nS= R2nin/ R1,nH= R9nin/ R10, nR= nout。
设差速机构特征参数值为k,由正号WW型2Z-X机构[1]的运动特性方程nS+(k-1)nH- knR=0,易得传动比i表达式为:

令ω2= R2/ R1、 ω9= R9/ R10, 如图2所 示,ω2和 ω9在0°~240°角位移范围内均是线性段,在240°~360°范围内均是非线性段,不难写出ω2和 ω9在0°~240°角位移范围内的方程[2]:

式中,t为角位移;s2、 s9为第一、二非圆齿轮对线性段传动比倒数幅值;r2、 r9为第一、二非圆齿轮对线性段传动比倒数

图2 0相位差传动比倒数
为使非圆齿轮节曲线封闭连续、极径适当,通常取r2= r9=1,非线性段采用正弦曲线。初始位置相位差为0,故0°~240°角位移范围内有恒定的总传动比[3], 记作i,特殊0地,取t=0、120°、240°,则分别有:

即:i0=1、s2=(k-1)s9, 则:

设ω2相对ω9左移为负、右移为正,且-1 2 0≤t2-t9≤120,则:

由于s2<1恒成立,所以无级变速器的总传动比范围为:

因此,只要给定差速机构特征参数值k和ω9线性段幅值s9,就能得到相应的传动比范围。为增强齿轮及其加工刀具的通用性,可使两非圆齿轮对形状完全一样,取差速机构特征参数值k=2。考虑到非圆齿轮对节曲线的形状以及可加工性,通常ω2线性段幅值s2<0.5且越小越好,本文取0.32,故总传动比取值范围为i∈[25/29,25/21],如图3所示,该范围可作为高速挡使用,若要将传动比扩大,只需在非圆齿轮无级变速器后串联副变速器,实现如图4所示的分段无级变速,具体方法本文不作详述。

图3 无级变速器传动比范围

图4 总传动比范围
图5表示一个周期内,一个分支的非圆齿轮对在相位差,即t2- t9=0°、-120°、120°时输出定传动比倒数1/i与角位移的关系,由图可知,定传动比只出现在ω2、 ω9的公共线性段角度范围,其余角度输出传动比是波动的,此时需要中断该组分支的动力,改由其他分支提供,而在相位差为±120°时每组分支公共线性段达到最小,为1/3周期,所以只有通过3组分支连续接力才能实现一个周期的定传动比传动。因此,用于控制动力切换的锥形离合器是实现无级变速的关键部件。

图5 单分支非圆齿轮对不同相位差时传动比倒数
2.2 锥形离合器结构及工作原理
锥形离合器由内锥盘、外锥盘、轴套、回位弹簧等组成,动力从与非圆从动齿轮同速的外锥盘输入,通过摩擦作用传至内锥盘,经由与内锥盘键连接的轴套输出至差速机构,其结构及动力传递路线如图6所示。当某一分支的非圆齿轮对传动比倒数处于非公共线性段时,差速机构不能输出定传动比,该组动力需要切断,此时凸轮推动该分支的锥形从动件径向向外运动,使得轴承推动内锥盘轴向内移,压缩回位弹簧,内、外锥盘的摩擦面相互分离,动力中断,完成分离过程;当该分支的非圆齿轮对传动比倒数重新处于公共线性段时,锥形从动件径向回落,在回位弹簧作用下,内锥盘轴向外移,内、外锥盘接合,动力恢复传递,完成接合过程。

图6 锥形离合器结构及动力传递路线
3 仿真模型的建立
相位差不为0时,每组锥形离合器接合时内、外锥盘的角速度差并非最大,得到仿真结果说服力不强,而在同一分支中的两组锥形离合器的工况类似,故对0相位差时单分支机构中的一组锥形离合器进行研究即可。
根据某特种车匹配发动机的参数要求,参考《机械设计手册》[4]设 计方法,经计算初步得到结构参数如表1所示。利用Solidworks和ADAMS/View软件建立锥形离合器模型时,在不影响机构正常运动的前提下,进行了合理简化[5],如:不考虑倒角、小孔等细节特征,用运动副代替了轴承等结构,简化后的仿真模型如图7所示。
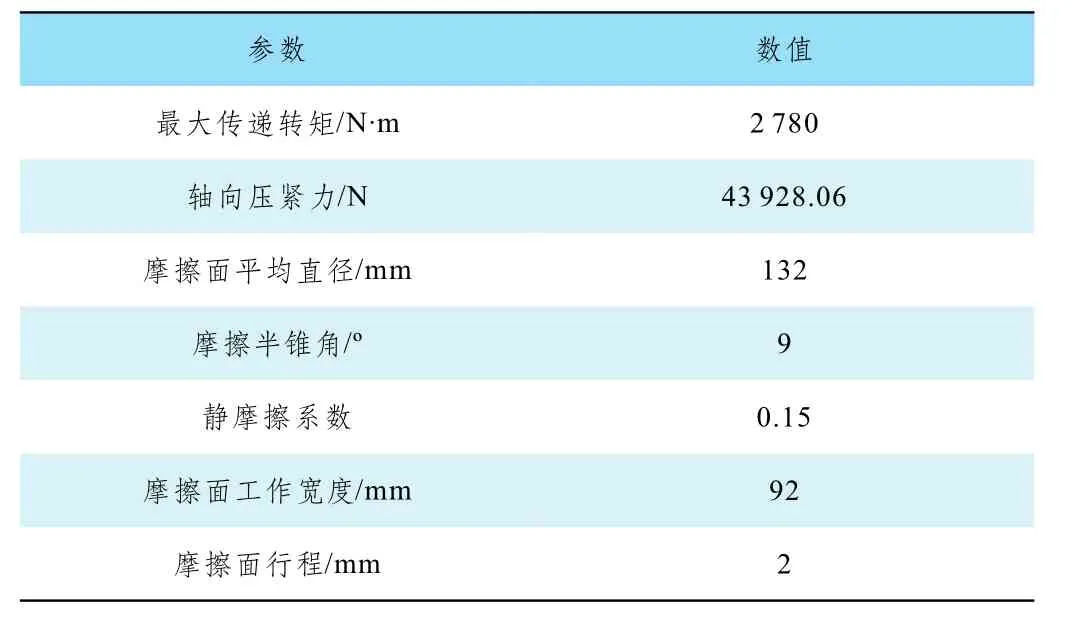
表1 锥形离合器结构参数

图7 仿真模型
4 动力学仿真分析及优化设计
4.1 仿真结果分析
图8表示了锥形离合器在一个周期内的冲击情况,由图可知,在动力切换过程中,内、外锥盘在0.16 s左右分离,未出现自锁、分离不彻底等现象。分离后,内锥盘由于惯性保持恒角速度运动;内、外锥盘在0.24s左右开始接合,内锥盘角速度迅速减小并向外锥盘角速度靠拢,约在6.19×10-4s后两者角速度达到一致,两者完成接合,仿真结果基本符合变速器传动原理,证明了其可行性及机构设计的正确性;另外,锥形离合器接合过程对应凸轮转角为9.29°,约占周期的1/36,体现了动力切换的快速性。

图8 锥形离合器冲击情况
在锥形离合器接合过程中,内锥盘角加速度的最大值为2.02×107° /s2,内、外锥盘间接触力的最大值达到3.96×105N,由于半锥角为9°,此时锥形离合器转动惯量稍大,这会导致其接合冲击力很大的同时内锥盘的惯性力偶矩也很大,影响接合过程的稳定性,故需对锥形离合器进行优化设计以减小接合冲击。
4.2 锥形离合器的优化设计
4.2.1 锥形离合器的半锥角优化
其他条件不变,只改变内、外锥盘半锥角,分别得到3°、4.5°、6°、7.5°半锥角的锥形离合器一个周期内的冲击情况如图9所示,各锥角锥形离合器的接合时间、接合冲击如表2所示。

图9 不同半锥角锥形离合器冲击情况
由图9和表2的仿真结果可得,其他条件一定时,各半锥角锥形离合器动力切换时间准确,且均未出现自锁、分离不彻底等现象;半锥角越大,锥形离合器接合时间越短[6],接合过程中内、外锥盘接触力最大值越大,内锥盘角加速度最大值越小;不同半锥角的锥形离合器滑磨功率变化趋势相近,虽然峰值相差较大,但整个接合过程的滑磨功相差较小,故可认为半锥角对滑磨功影响不大。为了直观地了解不同锥角锥形离合器的接合过程,根据表2中数据绘制柱状图如图10所示,根据图中各数据随半锥角的变化分析可得,半锥角大于6°时,接合时间、内锥盘角加速度最大值变化量小,减小趋势放缓;虽然接触力最大值有所增加,但由于接触力处于峰值附近的时间极短,故不会对锥形离合器的接合稳定性造成大的影响,综上所述,选定6°为较优半锥角。

表2 各锥角锥形离合器的仿真结果
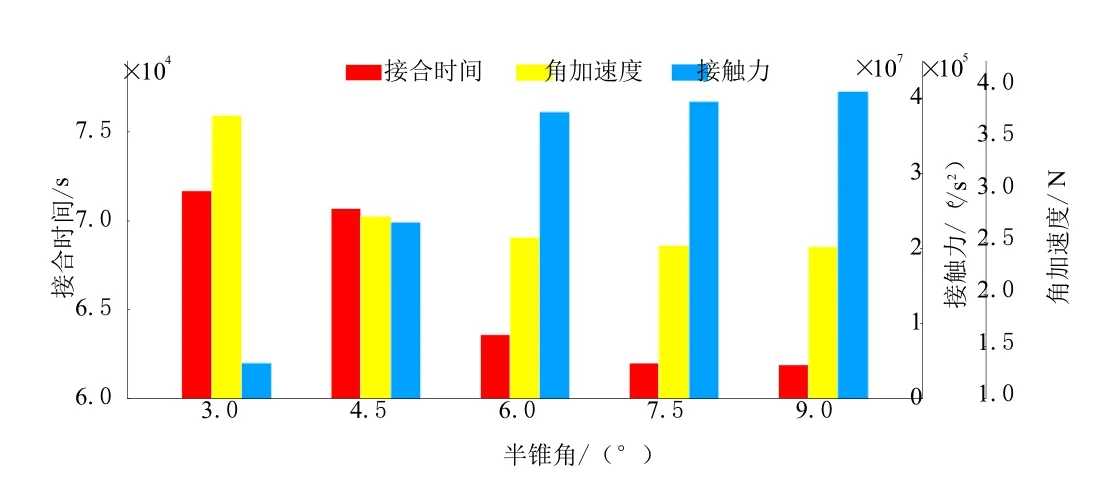
图10 各锥角锥形离合器接合情况柱状图
4.2.2 锥形离合器的静摩擦系数优化
在半锥角优化结果的基础上,其他条件不变,只改变内、外锥盘间静摩擦系数,分别得到静摩擦系数为0.1、0.12、0.18、0.2的锥形离合器一个周期内的冲击情况如图11所示,各静摩擦系数下锥形离合器的接合时间、接合冲击如表3所示。
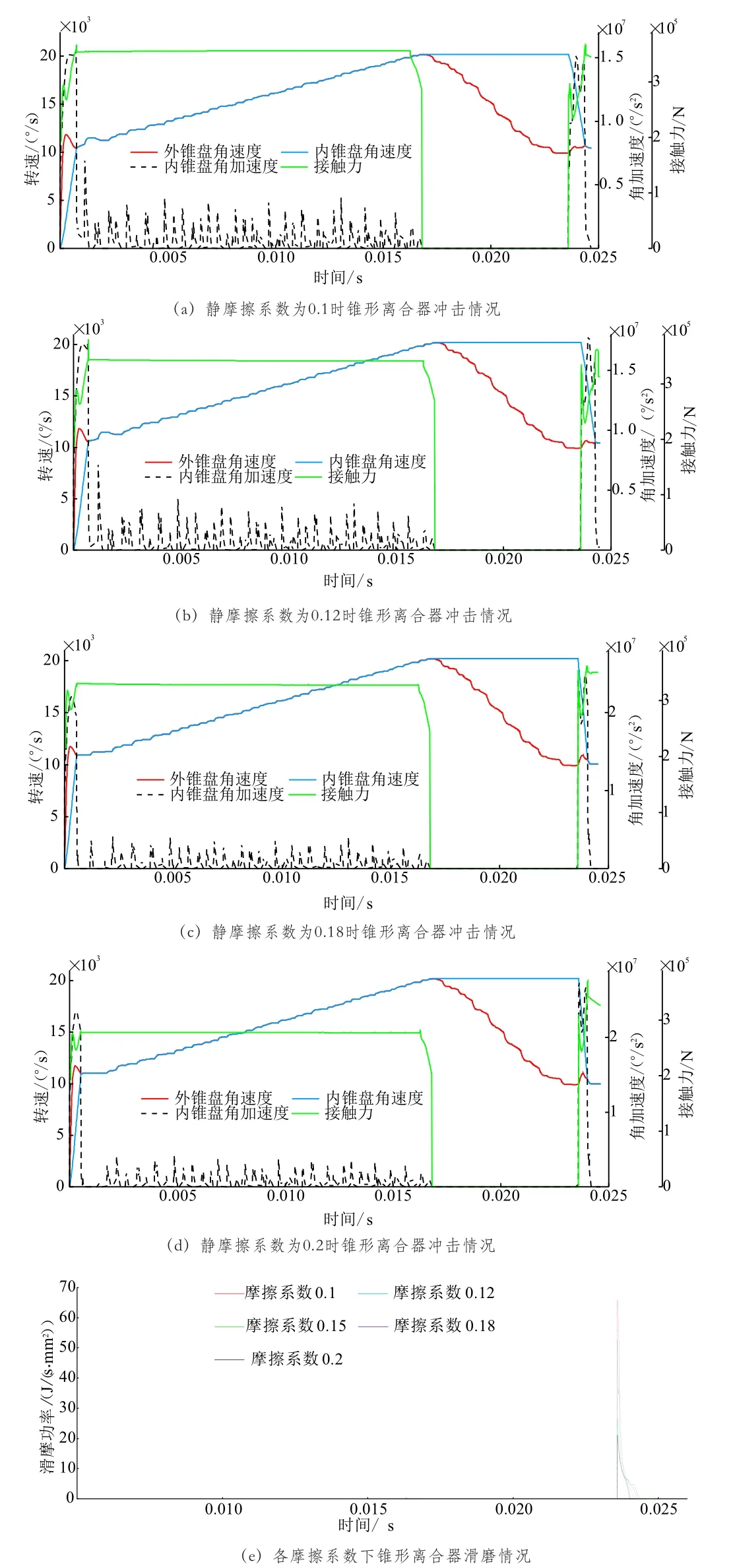
图11 各静摩擦系数下锥形离合器冲击情况

表3 各静摩擦系数下锥形离合器的仿真结果
由图11和表3的仿真结果可得,其他条件一定时,各静摩擦系数下锥形离合器动力切换时间准确,且均未出现自锁、分离不彻底等现象;静摩擦系数越大,锥形离合器接合时间越短,接合过程中内锥盘角加速度最大值越大,但静摩擦系数对内、外锥盘接触力最大值影响较小;不同摩擦系数锥形离合器接合滑磨功率变化趋势相近,且摩擦系数越大,滑磨功率峰值越小,整个接合过程的滑磨功越小[7]。为了直观地了解不同静摩擦系数下锥形离合器的接合过程,根据表3中数据绘制柱状图如图12所示,根据图中各数据随静摩擦系数的变化分析可得,半锥角为6°的锥形离合器在内、外锥盘的静摩擦系数小于0.15时,接合时间增加近30%,导致内、外锥盘磨损大大增加,降低传动效率;静摩擦系数大于0.18时,内锥盘角加速度最大值增加近30%,导致惯性力偶矩大大增加,内、外锥盘冲击较大,降低锥形离合器使用寿命;相比于优化前,静摩擦系数为0.18时,内、外锥盘接合时间相对较短、接触力最大值相对较小,虽角加速度最大值有所增加,但增幅不大,故不会对锥形离合器的接合稳定性造成大的影响,综上所述,选定0.18为较优静摩擦系数。

图12 各静摩擦系数下锥形离合器接合情况柱状图
5 结语
结合某特种车拟采用的非圆齿轮无级变速器中锥形离合器的工作原理及性能特点,建立了相关机构的虚拟样机模型,重点对锥形离合器在动力切换过程中的冲击情况进行动力学仿真分析,并从半锥角和静摩擦系数两方面对锥形离合器进行优化设计,结果表明半锥角为6°、静摩擦系数为0.18的锥形离合器接合冲击更小,稳定性更好,为后续的实物设计、加工、试验提供了理论参考。

