双向偏转平台动力学仿真与耦合分析

徐永帅， 陈 纯*， 赵知辛， 刘崇智, 陈 周

(1.陕西理工大学 机械工程学院， 陕西 汉中 723000;2.中航飞机股份有限公司 长沙起落架分公司， 陕西 汉中 723001)

五轴联动数控机床是加工制造复杂、高精度零件的必备设备之一，在我国制造业发展的道路上留下了浓墨重彩的一笔[1-3]。目前我国在五轴联动数控机床上使用最多的就是龙门式和摇篮式这两种数控机床，龙门式五轴联动数控机床是将原来的三轴数控机床主轴变为AC双摆头演变而来，而摇篮式五轴联动数控机床是在其AC摇篮里安装了十字双向滑动工作台演变而来。

但是在要求加工一些复杂的、具有一定倾斜角度的零件时，单靠五轴联动数控机床往往不能实现设计的要求，或者加工起来比较困难，工序也比较繁琐。因此本双向偏转平台主要是与五轴联动数控机床相配合，利用其可以在x,y两个方向上各能偏转±45°的特点来配合五轴联动数控机床加工一些复杂的、具有一定倾斜角度的零件，从而降低机床加工的难度，简化加工工序，提高加工的精度[4-5]。目前，国内外主要对数控工作转台的机械结构、控制系统、定位精度以及工作的稳定性与可靠性等方面进行研究[4]。对于如何提高数控工作转台的定位精度、工作的稳定性与可靠性以及如何改善系统的动力学性能等都是我们所关注的问题[6-8]。

多体动力学理论和虚拟样机技术为机床的动力学分析设计提供了一种新理念、新方法[9-11]。本文依据多体动力学理论和虚拟样机仿真技术，以某双向偏转平台为研究对象，运用软件建立三维模型，运用多体动力学理论建立动力学模型，从理论层面上推导数控工作转台各框架间的耦合情况[12]，运用动力学仿真软件ADAMS对其进行动力学仿真，对仿真所得出的数据和图像进行分析[13-15]。

1 双向偏转平台三维模型的建立

首先在Catia中建立双向偏转平台的三维模型，如图1所示。

该双向偏转平台共有两个自由度，分别是绕x轴的转动和绕y轴的转动，在该双向偏转平台中，外导轨与外齿轮固连在一起，内导轨与内齿轮固连在一起，电机11安装在底座上，驱动外齿轮绕x轴转动，从而带动工作平台绕y轴转动。电机2安装在内导轨导向块座上，内消隙齿轮8安装在电机2的轴上，并与内齿轮啮合来驱动内齿轮绕x轴转动，从而带动工作台转动。双向偏转平台的主要性能参数如表1所示，材料属性见表2。

1-工作台，2-内驱动电机，3-外导轨，4-外齿轮，5-导向块，6-底座，7-内导轨,8-内消隙齿轮，9-内齿轮，10-内导轨导向块座，11-外驱动电机图1 双向偏转平台三维模型

参量取值转台最大回转直径/mm325x轴向最大转角/(°)±45y轴向最大转角/(°)±45

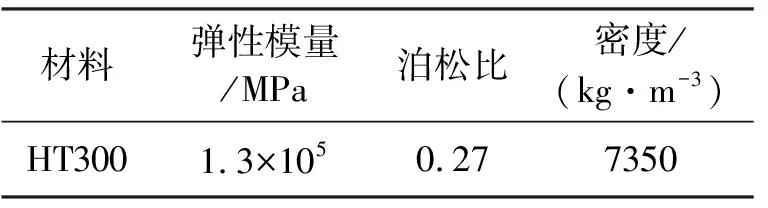
表2 双向偏转平台材料属性

2 双向偏转平台动力学模型的建立

为了便于建立双向偏转平台的动力学模型，这里首先将该双向偏转平台的机械结构进行简化，简化为如图2框架结构图。图中外齿轮通过转动副与工作平台相连接，内齿轮同样通过转动副与工作平台连接，内齿轮置于外齿轮之内，并间接的与外齿轮连接，A轴、B轴分别通过电机2、1驱动。然后建立其动力学方程和耦合方程。在这里首先建立三个坐标系：惯性坐标系为O-x0y0z0，双向偏转平台A轴坐标系为O-x2y2z2，双向偏转平台B轴坐标系为O-x1y1z1，在坐标系O-x1y1z1中y1与机座固连，在坐标系O-x2y2z2中，x2通过内齿轮间接的与外齿轮相连。设内齿轮绕x1、y1、z1轴旋转的转动惯量分别为Jx1、Jy1、Jz1，外齿轮绕x2、y2、z2轴旋转的转动惯量分别为Jx2、Jy2、Jz2。

在此机构中，两个电机为其动力源，基于Newton-Euler法动力学方程，采用旋转矩阵法假设在电机2的驱动下，惯性坐标系O-x0y0z0先以角速度β′绕y0逆时针旋转β度，旋转到O-x2y2z2。然后在电机1的驱动下，坐标系O-x2y2z2再以角速度α′绕x2逆时针旋转α度，旋转到O-x1y1z1，如图3所示。

图2 双向偏转平台框架结构图 图3 坐标系转换图

通过上述旋转变换，假设坐标系O-x0y0z0通过变换矩阵T(y,β)变换到坐标系O-x2y2z2，坐标系O-x2y2z2通过变换矩阵T(x,α)变换到坐标系O-x1y1z1,则变换矩阵T(y,β)、T(x,α)分别为

(1)

当坐标系从O-x0y0z0变换到O-x1y1z1，再从O-x1y1z1变换到O-x2y2z2后，则坐标系中必然存在某一点随着坐标系的变换而变换，假设这一点在惯性坐标系O-x0y0z0中的坐标为[x0,y0,z0]T，变换到新坐标系O-x′y′z′中的坐标为[x′,y′,z′]T，则有：

[x′,y′,z′]T=T(α,β)·[x0,y0,z0]T，

(2)

(3)

2.1 速度耦合

由以上所述可知，在该双向偏转平台中，外齿轮通过外导轨与底座相连接，内齿轮通过内导轨与外齿轮相连接，因此在此双向偏转平台系统中，外齿轮的动力由电机2直接提供，其角速度也只与自身的转动有关，在坐标系O-x2y2z2中外齿轮绕y2轴以角速度β′旋转β度，则有：

ωx2=0,ωy2=β′,ωz2=0。

(4)

在坐标系O-x1y1z1中，内齿轮的转动由内齿轮自身绕x1的转动和随外齿轮的转动而转动这两部分组成，设内齿轮相对于外齿轮绕x1轴以角速度为α′转动α度，则有：

(5)

从上述方程可以看出，当内齿轮和外齿轮同时转动时，会引起框架间的速度耦合，内齿轮绕各轴转动的角速度不光与自身的角速度有关，还与外齿轮的角速度有关。

2.2 转矩耦合

由上述分析可知，内齿轮的转动由两部分组成，分别是自身的转动和随外齿轮的转动而转动，而内齿轮除了有绕其转轴A轴的转矩外还有耦合在两个垂直方向上的转矩，内齿轮绕其转轴A轴转动所产生的转矩可表示为

(6)

内齿轮耦合在其转轴A轴的两个垂直方向上的转矩可表示为

(7)

(8)

故可得内齿轮绕其转轴A轴的转矩为

M1=Mx1=Jx1α″。

(9)

而外齿轮的转矩是由外齿轮自身的转动所产生的力矩和内齿轮的转动传递来的耦合力矩两部分组成，外齿轮自身转动所产生的力矩为

(10)

(11)

可得外齿轮的轴向转矩为

Jy2β″+Jy1β″cosβ+(Jx1-Jy1)α′β′sinα。

(12)

从上述方程可以看出，当内齿轮和外齿轮同时转动的时候，外齿轮的转矩不仅与外齿轮自身的转动有关，还与内齿轮有关，其转矩是由内齿轮和外齿轮叠加而成。

通过以上分析，我们可以发现当内齿轮与外齿轮同时转动时，框架间存在着速度耦合和力矩耦合，其耦合力矩与各轴的转动速度、角度以及转动惯量都有关系，通过以上动力学模型的建立，为该双向偏转平台控制系统的设计以及解耦问题的解决提供了理论依据。

3 动力学仿真与耦合分析

图4 双向偏转平台ADAMS模型

由于该双向偏转平台中含有大量的零部件，这样直接在ADAMS中仿真会给仿真带来不必要的麻烦，因此在不影响动力学仿真的情况下，将Catia建立的双向偏转平台的三维模型做适当的简化，以便于对双向偏转平台进行动力学分析。将简化后的三维模型导入ADAMS，如图4所示。给每个零件选择材料，选好之后，ADAMS软件会自动匹配出各个零件所对应的质量、密度及杨氏模量等物理属性。材料添加完之后再对各个零件创建相应的约束，然后对整个模型施加力。由于该双向偏转平台的最大工作载荷为392 N，因此这里定义一个重量为392 N的工件导入该模型中，并固定约束在工作台上，然后对该模型进行仿真分析。

由于该双向偏转平台的工作状态是匀速偏转，因此在这里只对其在匀速偏转的情况下做耦合分析。

3.1 内齿轮驱动电机输出扭矩比较

为了对比内齿轮单独偏转与内、外齿轮同时偏转两种情况下，内齿轮驱动电机输出扭矩的变化，这里分别对这两种情况进行仿真分析，得出内齿轮驱动电机输出扭矩曲线图，如图5所示。图中实线为内齿轮单独匀速偏转运动时驱动电机输出的扭矩曲线，虚线为内、外齿轮同时匀速偏转运动时驱动电机输出的扭矩曲线。

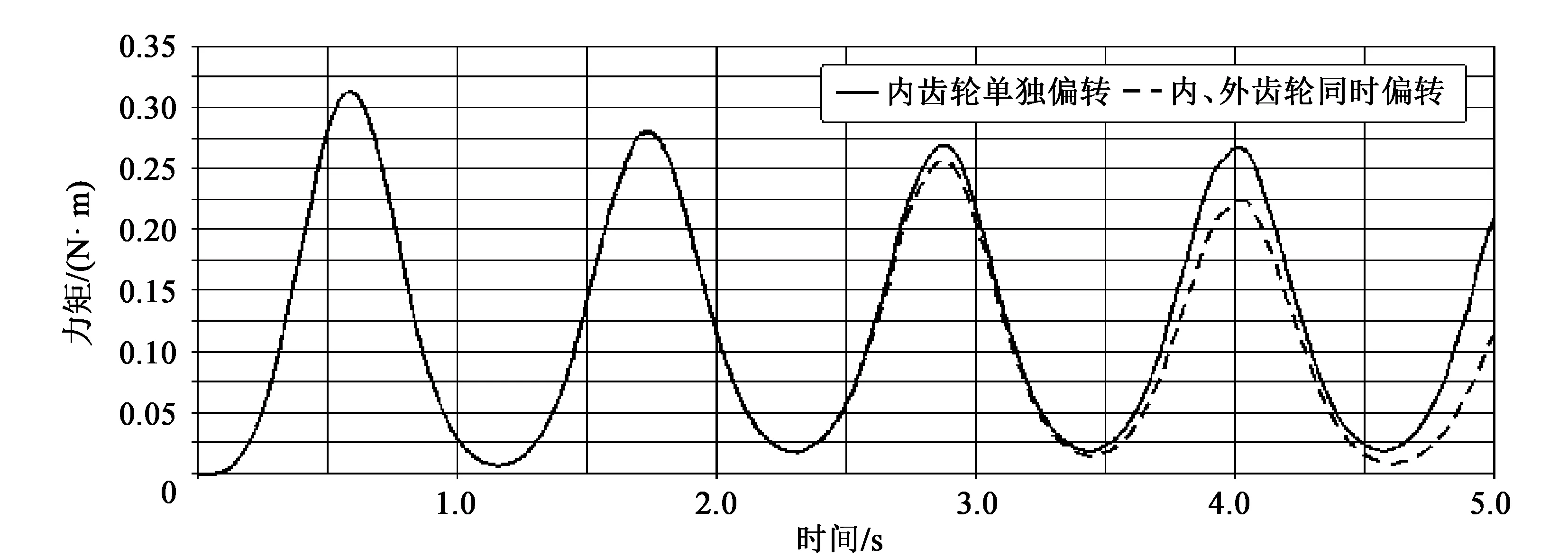
图5 内齿轮驱动电机扭矩对比图

从图5中可以得出当内齿轮单独做匀速偏转时，其驱动电机所输出的扭矩最大为0.313 N·m；当内、外齿轮同时做匀速偏转运动时，内齿轮驱动电机所输出的扭矩最大仍为0.313 N·m，其最大值变化率为0，且两条曲线几乎重合，只有在工作台快偏转至45°(工作偏转的极限位置)的时候出现略微的抖动。因此，说明内、外齿轮同时匀速偏转时对内齿轮驱动电机的扭矩几乎没有影响，无耦合作用，验证了理论计算的正确性。

3.2 外齿轮驱动电机输出扭矩比较

同理，为了对比外齿轮单独偏转与内、外齿轮同时偏转两种情况下，外齿轮驱动电机输出扭矩的变化，这里同样分别对这两种情况进行仿真分析，得出外齿轮驱动电机输出扭矩曲线图，如图6所示。图中实线为外齿轮单独匀速偏转运动时驱动电机输出的扭矩曲线，虚线为内、外齿轮同时匀速偏转运动时驱动电机输出的扭矩曲线。

图6 外齿轮驱动电机扭矩对比图

从图6中可以看出当外齿轮单独做匀速偏转时，其驱动电机所输出的扭矩最大为0.135 N·m；当内、外齿轮同时做匀速偏转运动时，外齿轮驱动电机所输出的最大扭矩增加至0.171 N·m，其最大扭矩增加了26.7%，且两条扭矩曲线相差较大。因此，说明内、外齿轮同时匀速偏转时对外齿轮驱动电机的扭矩影响较大，耦合作用明显，验证了理论计算的正确性。

4 结 语

以新型的双向偏转平台为载体，以ADAMS动力学分析软件为主要工具，运用虚拟样机技术，基于Newton-Euler法对某双向偏转平台进行耦合分析及动力学仿真，通过对比其在两个方向上分别单独偏转与同时偏转这两种情况下驱动电机所输出的扭矩，分析其耦合情况。得出当该双向偏转平台在两个方向上同时偏转时对内齿轮驱动电机扭矩的影响几乎为0，对外齿轮驱动电机扭矩的影响比较大，耦合作用比较明显，这为控制系统的解耦设计提供了一定的参考价值。