资本体现式技术进步率的变动趋势与我国增长悖论
侯玮迪 丁建勋 仪姗
内容摘要:基于一个具有两种类型技术进步的经济增长模型,本文推测,随着我国资本体现式技术进步水平的提高,经济增长率呈现出倒U型变动轨迹。文章运用2001-2015年我国省级面板数据的实证研究结果表明,我国整体以及东部、中西部地区的倒U型曲线都存在,而且全国整体以及东部和中西部地区都已经越过了全国拐点。这为2008年以后我国出现扩大投资下增长下滑的“增长悖论”提供了一个合理解释:除了全要素生产率增长率下降之外,设备资本品积累速度下降引致资本体现式技术进步速度降低,使经济增长率进入倒U型曲线的右侧,可能是另一个重要原因。
关键词:资本体现式技术进步 增长悖论 倒U型曲线
引言
自2008年以来,我国投资率大幅上升的同时GDP增长率却出现持续下滑,呈现出反常的“增长悖论”(赖平耀,2016)。许多学者也将“增长悖论”归因于全要素生产率增长率的下降(杨天宇、曹志楠,2015)。但还有学者认为,在现代社会的经济增长过程中,资本积累与技术进步往往是动态有机融合在一起的,通过全要素生产率的计算很难观察出这种资本体现式技术进步水平。一般认为,我国高投入中包含着全要素生产率没有包含的资本体现式技术进步(赵志耘等,2007;王士香和董直庆,2015)。
然而,按照上述观点,2008年以后我国大规模资本积累中应该蕴涵着巨大的技术进步,能实现经济的高速增长,但为什么还会出现扩大投资下增长的困境呢?这值得深入探讨。
我国“增长悖论”原因的理论分析
(一)资本体现式技术进步水平与经济增长率之间关系分析
下面本文将考察资本体现式技术进步与全要素生产率对经济增长的影响。假定总量生产函数为Y=AKαL1-α,其中Y为产出,L为劳动,K为资本,A为全要素生产率,α为资本的产出弹性。人均产出增长率为:
其中,gy为人均产出的增长率,gk为人均资本的增长率,gA为全要素生产率增长率。(1)式表明,人均产出增长率由人均资本增长率和全要素生产率增长率决定。如果考虑到资本中蕴含着技术进步,那么人均资本存量k的变化为:
其中,一个变量上加一点表示其对时间的导数,下同。i为人均投资,n为劳动力增长率,δ>0为折旧率。 在这里,本文引入了一个变量q>0,用它度量资本体现式技术进步水平。一般认为,在平衡增长路径上,当且仅当qi/k 的比值为一定值时,k/k 为一常数。因此可以得到gk=gi+gq。在平衡增长路径上,消费、投资和产出都以相同的速率增長,因此有gi=gy。将 gk=gi+gq以及gi=gy代入gy=gA+agk,最终可以得到人均产出增长率与两种技术进步率之间的关系为:
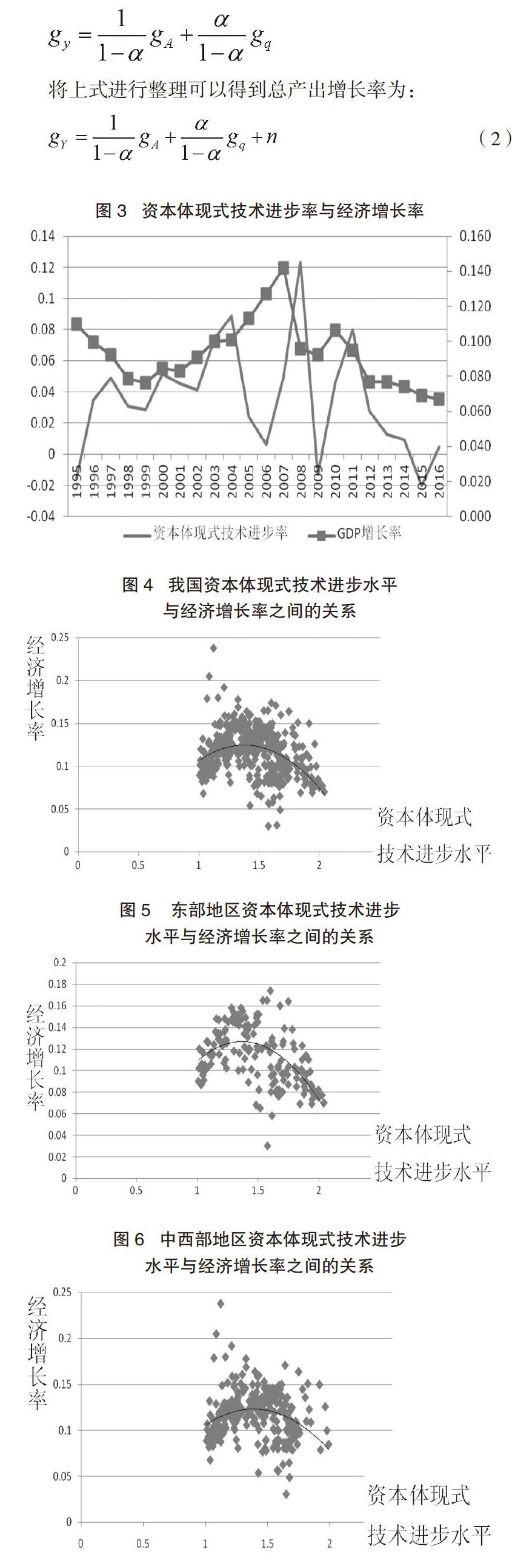
将上式进行整理可以得到总产出增长率为:
(2)式表明,总产出增长等于两种技术进步率加上劳动力增长的贡献。增长的源泉比传统的增长理论扩大了——是资本体现式技术进步与TFP共同作用的结果。
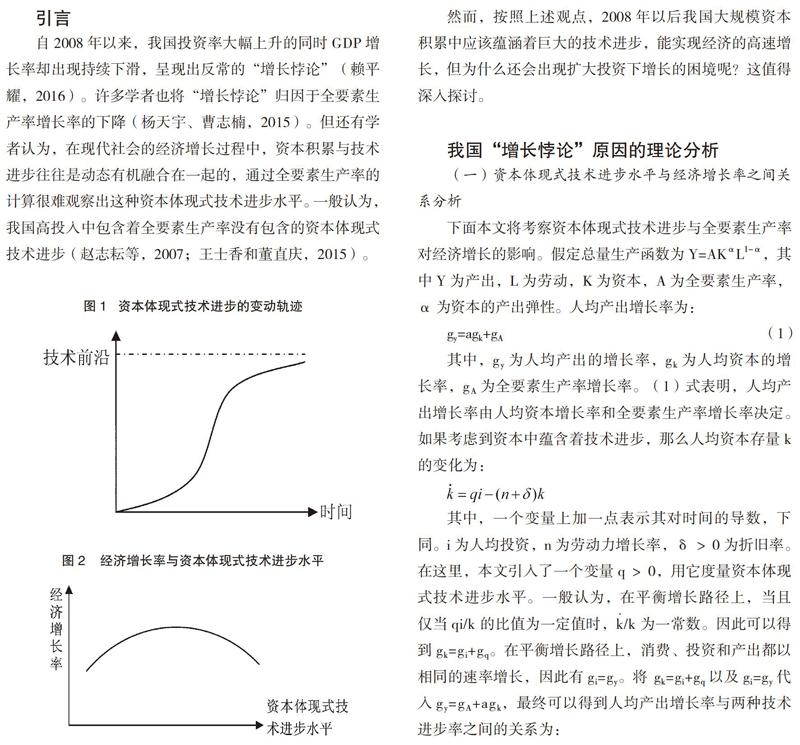
众所周知,实现中性技术进步主要依靠研发,而实现资本体现式技术进步主要靠技术引进。一般而言,资本体现式技术进步水平提高的过程可能会呈现出类似逻辑斯蒂曲线形状,即S型(见图1)。因为,当初始引进技术时,或存在昂贵的学习成本或存在学习期间受技术吸收能力的影响,技术进步速度可能并不快;但随着引入技术的经济体上述条件的改善,技术进步速率将变快;当逐渐接近技术前沿时,可供引进的技术越来越少,技术进步速度又会慢慢降低。也就是说,在资本体现式技术进步水平不断提高的过程中,资本体现式技术进步率将经历低→高→低的变动过程,如果不考虑其他因素的影响,经济增长率也将会经历低→高→低的变动轨迹。如果将资本体现式技术进步水平和经济增长率放到一个坐标系中,横轴为资本体现式技术进步水平,纵轴为经济增长率。那么,随着资本体现式技术进步水平的提高,经济增长率会呈现出倒U型变动轨迹(见图2)。
(二)我国“增长悖论”原因的推测
基于理论分析,本文考察我国资本体现式技术进步率的变动情况。虽然技术进步是与资本融合在一起的,但不同类型的资本品所包含的技术进步并不相同。建筑资本质量基本保持不变(宋冬林等,2011),设备投资品的技术进步率几乎可以代表整体经济的资本体现式技术进步率(赵志耘等,2007)。而在1984-1995年间,我国各行业设备资本存量增长率年均为14.1%,远高于建筑资本存量年均7.3%的增长速度,1993-2005年期间,各省设备资本存量增长了9.7倍,建筑资本平均增长了6.1倍(赵志耘等,2007)。因此,改革开放以来,由于设备资本的积累速度基本上经历了一个先增速后减速的过程,所以资本体现式技术进步率(测算方法见赵志耘(2007))也应经历一个先提高后降低的过程(见图3)。
基于上述理论分析,本文推测, 2008年以后我国大规模投资下经济增长率持续下滑,除了TFP增长率持续下降之外,设备资本积累速度降低引致资本体现式技术进步率下降,使经济增长率进入倒U型曲线的右侧,可能是另一个重要原因。
我国“增长悖论”原因的实证研究
(一)资本体现式技术进步水平与产出增长率的相关关系
本文首先利用散点图来考察核心解释变量与被解释变量间的相关关系。图4比较直观地描绘了我国资本体现式技术进步水平与经济增长率之间呈现的非线性关系。更确切地说,随着资本体现式技术进步水平的提高,经济增长率呈现出先上升后下降的倒U型变动趋势。
为了尽可能多地获得我国资本体现式技术进步水平与经济增长率的变动情况,本文分别画出了东部和中西部地区资本体现式技术进步水平与经济增长率的散点图及拟合线。如图5、图6显示,无论是东部还是中西部,在资本体现式技术进步水平提高过程中,经济增长率基本上呈现出倒U型变动轨迹。
但是,散点图和拟合线仅仅是对二者之间关系形态的大致描述,而要准确地判断资本体现式技术进步水平提高过程中经济增长率的变动轨迹,需更深入研究。
(二)资本体现式技术进步水平与经济增长率之间关系的计量分析
1.样本选取与数据来源。本文以我国30个省份(除西藏、台湾、香港和澳门)为实证研究对象,时间跨度为 2001-2015年。所用的原始数据来源于《中国统计年鉴》、各省的《统计年鉴》以及《新中国60年统计资料汇编》。
2.模型设定和变量说明。为了验证上述推测,本文建立如下计量模型:
其中, gi,t为第i省第t期产出增长率,本文是以2000年各省区不变价格度量的GDP增长率来衡量各省区的总产出增长率;qi,t 为第i省第t期资本体现式技术进步水平,测算各省资本体现式技术进步水平所用方法来源于赵志耘等(2007)。
根据理论模型,还有其他因素也影响经济增长率。本文在模型中加入了一些控制变量Xi,t,包括:劳动力增长率n;全要素生产率可以分解为产业结构变动和技术进步,为了分析产业结构变动和技术进步对TFP增长率的影响,本文加入产业结构si,t,以各省第一产业占GDP比重作为产业结构的代理变量;研发资本增长率r,研发资本存量为,其中IRi,t为第i省第t期的名义研发投资;δ 为折旧率,假定为5%;根据Young(2003)的方法用2000年投资额除以10%作为初始资本存量;Pi,t为第i省第t期固定资产投资价格指数(2000年=1);劳动力平均受教育年限增长率hi,t,作为人力资本增长率的代理变量,本文测算的是6岁以上人口的平均受教育年限增长率。ei,t为随机干扰项。
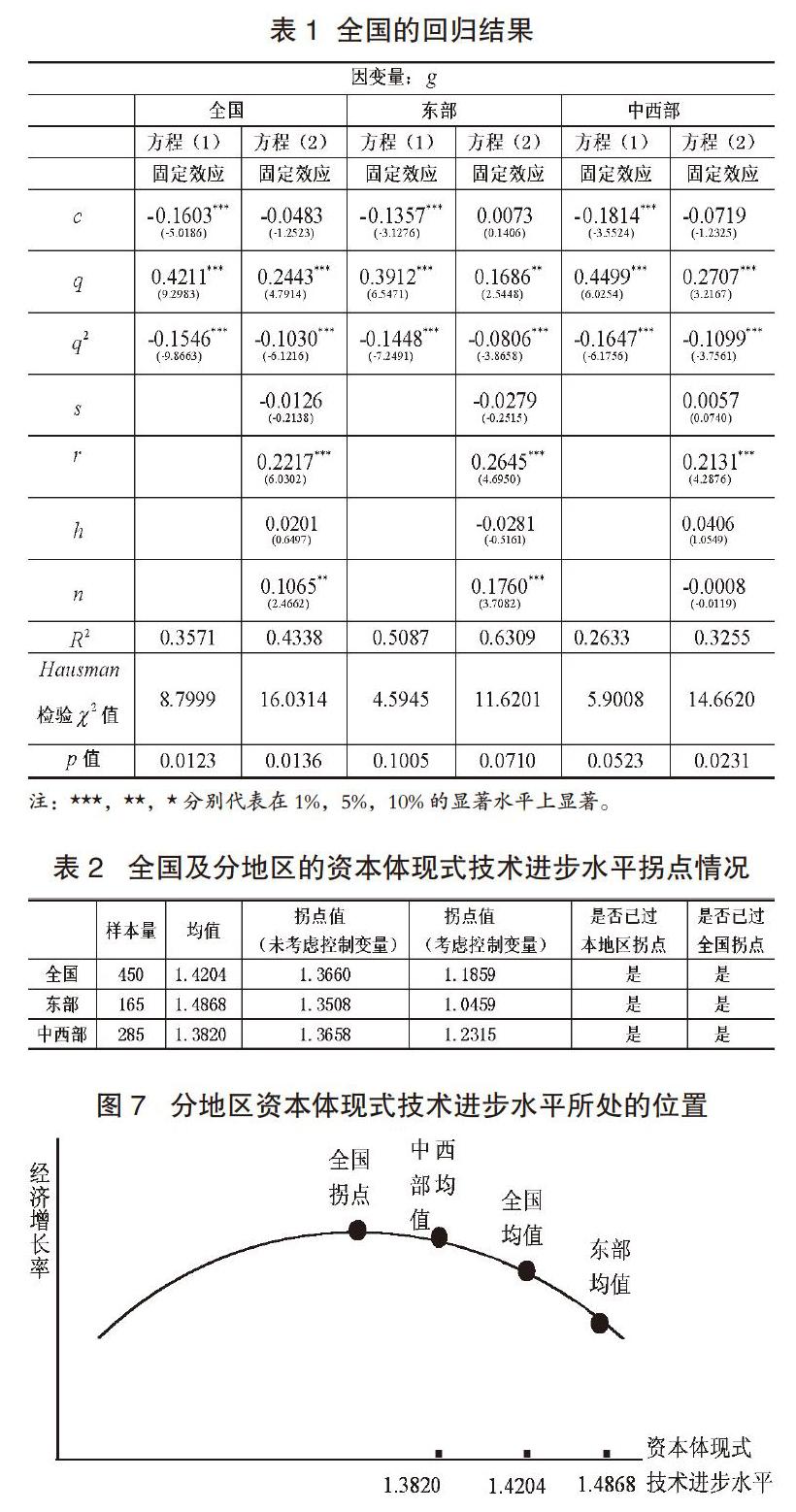
3.实证结果。文章运用我国30个省份2001-2015年的面板数据对模型(3)进行估计,结果如表1所示。根据Hausman检验结果,在所有的分析中均选择了固定效应模型。
首先看全国情况。方程(1)只考虑资本体现式技术进步水平与经济增长率关系,结果显示,q的系数显著为正,q2的系数显著为负,意味着资本体现式技术进步水平提高过程中经济增长率的确呈现出倒U型变动轨迹。方程(2)加入了其他一些变量,估计结果显示,q和q2的符号仍保持不变,且在统计上显著。这表明,在资本体现式技术进步水平提高过程中,经济增长率呈倒U型变动轨迹的结论仍然成立。其他变量,第一产业占GDP比重s以及平均受教育年限增长率 的系数都为负但不显著,而研发资本增长率r以及劳动增长率n的系数显著为正。
其次看区域情况。表1结果中东部和中西部的结果均显示,q的系数显著为正,q2的系数显著为负。这意味着,基于地区层面的研究结果与全国层面的研究结果完全一致。其他变量,第一产业占GDP比重s和平均受教育年限增长率h的系数符号在地区间并不相同但都不显著;在所有的地区中研发资本增长率r的系数显著为正;劳动增长率n的系数符号以及显著性在地区间也存在差异。
下面,本文对倒U型曲线的拐点进行研究,以明确目前我国资本体现式技术进步水平与经济增长率的组合是否已进入倒U型曲线的下降段,从而判断本文对我国“增长悖论”形成原因的推测。
由表1全国层面估计结果中的方程(1)可推知,曲线的拐点q*全国=1.3660 ,如果考虑其他控制变量,由方程(2)可推知,U型曲线的拐点 q*全国=1.1859。而对于全国的样本而言,资本体现式技术进步水平的均值为1.4204,高于1.3660和1.1859。这表明,目前我国整体资本体现式技术进步水平已超过了拐点,进入了倒U 型曲线的下降段。文章分別运用东部和中西部地区方程(1)和(2),推算出(未)考虑控制变量情形下各地区U 型曲线拐点对应的资本体现式技术进步水平值,并与各地区的实际均值进行比较,见表2所示。数据显示,各地区资本体现式技术进步水平的均值均已超过了全国以及各地区自身的拐点值,进入了倒U型曲线的右半支。图7给出了全国以及各地区资本体现式技术进步水平均值所处倒U曲线的位置。可以看到, 同处于全国拐点右侧,东部和中西部地区的位置并不相同,中西部地区均值点位于全国均值点的左边,对应的经济增长率要高于全国,而东部地区均值点位于全国均值点的右侧,经济增长率要比全国低,这正好与表2中q的系数大小基本一致。
综上分析,可以得出如下结论:在资本体现式技术进步水平提高的过程中,我国经济增长率呈现倒U型变动轨迹。全国及东部和中西部地区都已经越过了全国以及各地区自身的拐点。这为近年来我国扩大投资下增长下滑的“增长悖论”提供一个合理解释——虽然我国资本体现式技术进步水平不断提高,但由于设备资本积累以及资本体现式技术进步经历先加速后逐渐减速的过程,使资本体现式技术进步水平和经济增长率组合进入了倒U曲线的右半支,经济增长开始减速。
主要结论与政策启示
基于一个具有两种类型技术进步的经济增长模型,本文推测,随着我国资本体现式技术进步水平的提高,经济增长率呈现出倒U型变动轨迹。文章运用2001-2015年我国省级面板数据进行实证研究,结果表明,我国整体以及东部、中西部地区的倒U型曲线都存在,而且全国整体以及东部和中西地区都已经越过了全国拐点。这为2008年以后我国出现扩大投资下增长下滑的“增长悖论”提供了一个合理解释:除了全要素生产率增长率下降之外,设备资本品积累速度下降引致资本体现式技术进步增速降低,使经济增长率进入倒U型曲线的右侧,可能是另一个重要原因。基于以上分析,可以得到对我国未来经济增长有意义的政策建议:
第一,从全国整体而言,应适时调整和转换经济增长的主要引擎。一定要充分认识资本体现式技术进步影响经济增长的特性,不能总依赖资本积累促进资本体现式技术进步来实现经济的高速增长。必须根据经济发展阶段,适时对经济增长的主要引擎进行调整,实现经济增长由主要依靠资本体现式技术进步向主要依靠非体现式技术进步转换。当然,实现经济增长主要引擎的转换,并不意味着我们再不需要资本体现式技术进步。必须承认,我国和发达国家之间还存在着技术差距,欲实现我国经济的持续增长,还需要继续引进先进设备促进资本体现式技术进步,特别鼓励引进技术(包括节能技术和减排技术)含量高的设备。但是,必须处理好技术引进与自主创新的关系,匹配好资本体现式技术进步与非体现式技术进步的组合,才能实现我国经济的持续增长。
第二,就各地区而言,应选择适宜的技术进步类型以促进自身经济增长。尽管我国东部和中西部地区的资本体现式技术进步水平均值已超过了全国拐点,但不同地区所处倒U曲线的位置毕竟还存在差异。因此,不同地区的技术进步促进政策也存在差异。与全国情形一样,东部地区要重视技术引进但更要重视研发,实现经济增长的主要引擎由资本体现式技术进步向非体现式技术进步转换,而中西部地区尤其是中西部地区的落后地区可能正处于拐点处或刚刚越过拐点,资本体现式技术进步尚处于能促进经济高速增长的阶段,因此这些地区还不能忽视促进资本的有效积累,需要继续采用资本体现式技术进步促进经济的快速增长。当然,这也并非意味着这些地区不需要进行研发。这是因为,通过技术引进取得的技术创新,往往并不完全符合地区的资源禀赋。当引进先进机器设备后,在不影响所生产产品质量的前提下,可以对设备的一些流程进行研发创新改造,使之尽量符合地区禀赋结构。同时,对于一些根本无法引进的技术或者仅有一两个关键技术无法引进,这就必须进行自主创新和研发。
参考文献:
1.赖平耀.中国经济增长的生产率困境:扩大投资下的增长下滑[J].世界经济,2016,39(1)
2.杨天宇,曹志楠.中国经济增长速度放缓的原因是“结构性减速”吗?[J].中国人民大学学报,2015,29(4)
3.赵志耘,吕冰洋,郭庆旺,贾俊雪.资本积累与技术进步的动态融合:中国经济增长的一个典型事实[J].经济研究,2007(11)
4.宋冬林,王林辉,董直庆.资本体现式技术进步及其对经济增长的贡献率(1981-2007)[J].中国社会科学,2011(2)
5.王士香,董直庆.资本体现式技术进步视角下的资本质量提升[J].东北师大学报(哲学社会科学版),2015(3)

