基于自适应阈值和形态学的改进分水岭分割算法*
罗 山,张冬梅
(攀枝花学院交通与汽车工程学院,四川 攀枝花 617000)
0 引言
分水岭比较经典的计算方法是L.Vincent提出的[1],一些学者对传统的分水岭算法提出了改进。毕浩宇等人提出了一种基于形态学分水岭算法的图像分割改进算法[2]。孙惠杰等人提出了一种基于粒子群和区域生长的改进分水岭算法,有效地解决了分水岭算法的过分割问题,分割结果更加有效、准确[3]。张秀再等人提出了一种阈值自适应的Sobel边缘检测算法[4]。
针对分水岭分割算法的不足[5],本文对传统分水岭算法进行改进。首先通过中值滤波抑制噪声,采用多模板Sobel算子求梯度;然后对梯度图像进行数学形态学运算,得到重建图像,该操作保留了图像区域重要轮廓,同时去除了噪声和细节;接着对重建图像应用Otsu算法,得到自适应阈值分割图像,该操作增强了系统鲁棒性;最后对上述结果作分水岭变换,实现精确分割。
1 数学形态学处理
数学形态学是一门基于集合论的非线性学科,其基本思想是利用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的。有膨胀、腐蚀、开启和闭合四种基本运算,利用这些基本运算可以组合成多种实用的数学形态学算法。
设f表示图像,B表示结构元素,x表示平移量,⊕表示膨胀运算符号,Θ表示腐蚀运算符号;则f被B膨胀的定义为:
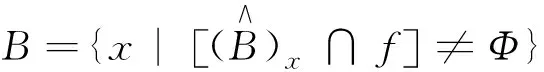
(1)
膨胀运算可以填补目标内部孤立的小孔洞,将背景边缘转化为目标的边缘,使目标增大而背景缩小。f被B腐蚀的定义为:
fΘB={x|(B)x⊆f}.
(2)
腐蚀运算可以消除目标外部孤立的噪声点,但也会丢失目标外边缘和内空边缘的一些信息,使目标缩小而背景增大。
设∘ 表示开启运算符号,·表示闭合运算符号;则开启运算的定义为:
f∘B=(fΘB)⊕B.
(3)
闭合运算的定义为:
f·B=(f⊕B)ΘB.
(4)
结构元素对处理效果有决定性影响。小尺度结构元素的去噪能力弱,检测到的边缘比较细,边缘定位较准确且边缘细节丰富;大尺度结构元素的去噪能力强,检测到的边缘比较粗,会丢失部分小的边缘细节。
本文采用多尺度多种类型的结构元素对梯度图像进行开闭重建运算,得到的重建图像保留了图像区域重要轮廓,同时去除了噪声和细节。
2 自适应阈值分割
本文使用了一种二维最大熵自适应阈值[6]选取方法,简称Otsu,避免了人为设定阈值的不合理性。Otsu自适应阈值分割算法步骤为:
1) 计算图像的归一化直方图pi;
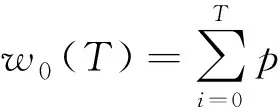
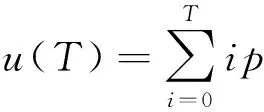
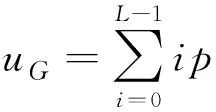
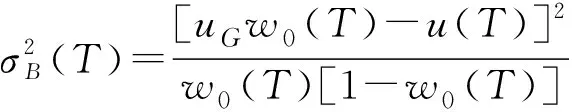
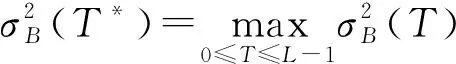
7) 用最佳阈值T*对图像进行分割。
图1(b)所示为对含噪图像中值滤波、数学形态学处理后自适应阈值分割的结果,可见,分割精度高,极大地减少了“过分割”和“欠分割”区域。
3 基于自适应阈值和形态学的改进分水岭算法
3.1 分水岭算法数学表示[7]
令g(x,y)表示一幅梯度图像,M1,M2,…,MR表示由所有区域极小值点构成的集合,用min与max表示g(x,y)的最小、最大算子。假设M[n]表示使g(s,t) M[n]={(s,t)|g(s,t) (5) M[n]的几何意义为图像g(x,y)中出现在平面g(x,y)=n下方的全部像素的坐标集合。假设A为一个连通集合,A中任意两点p,q的测地距离为A中连接p,q两点的最短距离。定义为: dA(p,q)=min{L(p)|p1=p,p1=q,p⊆A}. (6) 当K为A中的一个集合,它由s个连通子集K1,K2,K3,…构成,连通子集Ki的测地影响区IZ(Ki)定义为A中到Ki的测地距离小于到K中其他任意连通成分的距离的点的集合。定义为: IZA(Ki)={p∈A|∀j≠i,dA(p,Ki) (7) A中除K以外的测地影响区的点集合称为测地影响区骨架SKIZA(K)。定义为: (8) 假设图像为f(x,y),用CB(M)表示与区域极小域对应的积水盆地,CBh(M)表示该积水盆地上高度小于或等于h的点,即为分水岭变换。定义为: CBh(M)={p∈CB(M)|f(p)≤h}=CB(m)∩Tt≤h(f). (9) 综合以上论述,本文算法步骤为: 1) 原始图像经滤波降噪后,采用Sobel算子得到梯度图像; 2) 对梯度图像进行数学形态学开闭重建运算,得到重建图像; 3) 对重建图像应用Otsu算法,得到自适应阈值分割图像; 4) 最后对上述结果作分水岭变换,得到精确分割图像。 3.3.1 分割算法实现 3.3.2 结果分析 本文算法与传统算法性能对比分析如表1所示。 表1 两种算法之间的比较 传统分水岭算法未对图像进行滤波处理,且直接对梯度图像进行分水岭分割,产生了严重的过分割现象,如图1(c)所示。本文算法考虑图像边缘和细节信息,对其进行中值滤波去噪,对梯度图像进行形态学开闭重建运算,保留区域重要轮廓的同时去除了噪声和细节。从图2(d)可以看出,过分割得到了较好的抑制,产生的分割区域明显减少,边缘定位也更加准确,视觉效果更好,同时分割精度也有所提高。 实际图像受到噪声、阴影等诸多因素的影响,灰度分布不均匀,难以对图像进行准确分割。针对分水岭分割算法对噪声比较敏感和过度分割现象,本文提出了一种基于自适应阈值和形态学的改进分水岭分割算法。实验结果表明,该算法边缘提取更准确,具有很强的噪声抑制能力,较好地削弱了过分割现象,实现精确分割。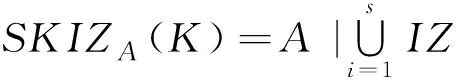
3.2 本文算法
3.3 实验结果及分析

4 结束语

