如何解决“圆圈里填数”的问题

例1.把 1、2、3、4、5这五个数分别填在图 1的中，使横行与竖列中三个圆圈里的各数之和相等。

图1

这道题是要在圆圈里填数，并且使横行与竖列中的三个圆圈里的各数之和相等。在填数之前，我们首先对这五个数进行具体的分析，如图2所示：

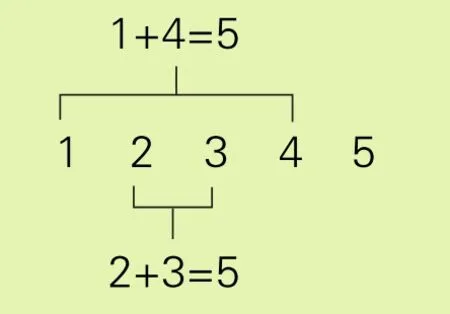
图2

从图2中可以看出，在这五个要填的数中，除5之外的数有这样的关系：1+4=5、2+3=5。我们根据这个特点，只要把5填在中间的圆圈里，把1和4、2和3这两组数分别填在左右或上下相对应的圆圈里就可以了。填法有许多种，其中两种填法如图3所示：

图3

用同样的方法，把1或3填在中间的圆圈里也能得到符合要求的答案，但2和4不能填在中间的圆圈里。

例2.将 1、2、3、4、5、6、7这七个数填入图 4的中，使每条线上三个圆圈里的各数之和都是10。

图4

解答这道题的关键是要确定图4中间圆圈里填几。我们可以这样想：每条线上都有三个圆圈，并且每三个圆圈里的数的和都是10，所以三条线上的九个数的和是10+10+10=30。1—7这七个数的和是1+2+3+4+5+6+7=28，30-28=2，这多出的2，是由于图4中间圆圈里的数重复计算了2次造成的，所以图4中间圆圈里应该填1。然后将2—7这六个数分成三组，使每一组的各数之和都为10-1=9，因为2+7=9、3+6=9、4+5=9，所以这三组数分别是：2和 7、3和 6、4和 5。将同一组数填到同一条线上的圆圈里。按照这种方法填数可以有许多种答案，其中一种如图5所示：

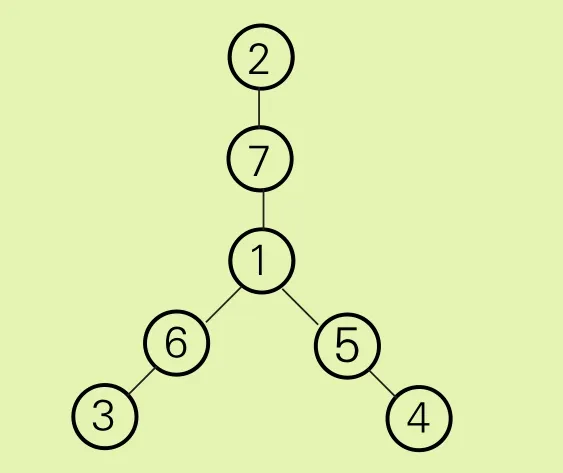
图5