基于修正近似双曲正切函数的平滑l0范数算法

陈金立，李 伟，朱筱嵘，陈 宣，李家强

(1.南京信息工程大学 气象灾害预报预警与评估协同创新中心，江苏 南京 210044；2.南京信息工程大学 电子与信息工程学院，江苏 南京 210044；3.南京信息工程大学 物理与光电工程学院，江苏 南京 210044)

0 引 言

在传统信号采样理论中，为保证信号的无失真输出，需要的采样率至少为信号带宽的两倍。因此，在处理较大带宽的信号时，传统信号采样会对硬件系统造成很大的压力。压缩感知(compressing sensing，CS)[1-3]是一种新型的信号采样理论，它只需要极少的稀疏信号采样值即可利用重构算法完成信号的精确重构，现已广泛地应用在雷达成像[4]、信号处理[5]以及医学成像[6]等领域。稀疏重构问题等价于欠定方程组y=Dx的稀疏求解问题，其中，y∈M为测量矩阵，D∈M×N是感知矩阵，x∈N是稀疏向量。稀疏问题的求解模型可表示为s.t.y=Dx。其中，表示l0范数，即向量非零元素的个数。l0范数最小化问题是NP-难问题，从而导致稀疏问题模型难以求解[7]。基追踪(basic pursuit，BP)算法[8]是解决上述问题的一种有效的算法，该算法利用l1范数来代替l0范数，由此上述模型转变为s.t.y=Dx，然后对其进行求解，从而实现对稀疏信号的重构。但是，BP算法的计算量较大，无法快速重构出稀疏信号。此外，还有许多其它稀疏重构算法，比如，迭代加权最小二乘(iterative re-weighted least squares，IRLS)算法[9]、正交匹配追踪(orthogonal matching pursuit，OMP)算法[10]以及平滑l0范数(smoothedl0norm，SL0)算法[11,12]等。其中，SL0算法利用高斯函数来逼近l0范数，并通过最速下降法和梯度投影原理实现稀疏信号的重构。尽管SL0算法能够快速重构稀疏信号，但是该算法所采用的高斯函数对l0范数的逼近性能较差，并且在利用最速下降法解决该函数极值问题时会产生“锯齿效应”，从而导致SL0算法的重构精度较低。文献[13]提出一种牛顿平滑l0范数(newton smoothedl0norm，NSL0)算法，该算法采用近似双曲正切函数来逼近l0范数，并利用修正牛顿法解决函数的极值问题，从而提高了SL0算法的重构性能。文献[14]采用另一种近似双曲正切函数来逼近l0范数，并在牛顿方向上搜寻该函数的极值，进而获得一种近似SL0(approximate smoothedl0norm，ASL0)算法，然后利用该算法进行MIMO雷达目标成像，有效地提高了其成像性能。

针对SL0算法中所采用的高斯函数对l0范数的逼近效果不理想从而导致算法的重构性能差的问题，本文提出一种基于修正近似双曲正切函数的平滑l0范数算法，该算法采用一种修正的近似双曲正切函数来对l0范数实现较优的逼近，并通过牛顿法求解该平滑函数所表示的稀疏问题，从而有效地提高了稀疏信号的重构性能。仿真结果表明，本文算法的重构性能优于SL0算法、NSL0算法以及ASL0算法。

1 基于修正近似双曲正切函数的平滑l0范数算法

1.1 一种用于逼近l0范数的修正近似双曲正切函数

SL0算法的核心思想在于采用高斯函数来逼近l0范数，从而将l0范数最小化问题转变成平滑函数的极值问题，避免了对l0范数最小化问题的直接求解。SL0算法所采用的高斯函数的表达式为

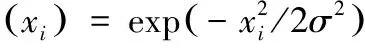
(1)

则

(2)

令

(3)

可以得到

(4)

则稀疏求解模型可转化为

(5)

为了提高SL0算法中的平滑函数对l0范数的逼近程度，文献[13]和文献[14]分别采用两种不同的近似双曲正切函数来代替标准高斯函数。这两种双曲正切函数表达式分别为

(6)

(7)

由此可知，寻找一种合适的平滑函数来有效的逼近l0范数，这对SL0算法的重构性能至关重要。在NSL0算法和ASL0算法的基础上，为了更进一步提高平滑函数对l0范数的近似程度，本文构造一种平滑函数来近似l0范数，从而提高其逼近程度。本文构造的一种修正近似双曲正切函数表达式如下

(8)

图1为高斯函数、文献[13]和文献[14]中分别采用的两种近似双曲正切函数以及本文所采用的修正近似双曲正切函数fσxi在σ=0.1处的分布图。由图1可以看出，与文献[13]和文献[14]中提出的两种近似双曲正切函数相比，本文提出的修正近似双曲正切函数在x∈[-0.5, 0.5]内的“陡峭性”更大，表明该函数对l0范数的逼近程度更优。

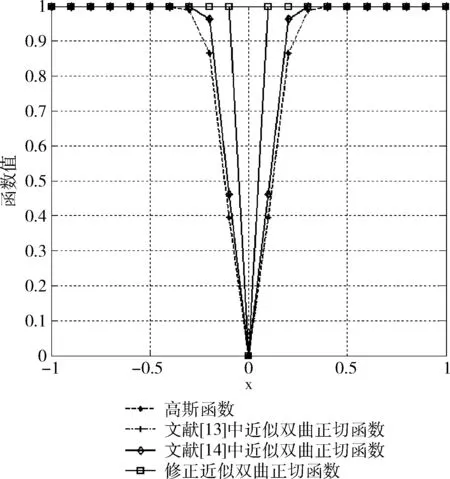
图1 4种函数在σ=0.1时的分布

令

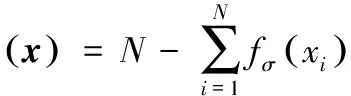
(9)

可以得到

(10)

则对应修正近似双曲正切函数的稀疏模型为

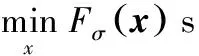
(11)

与文献[11-14]类似，参数σ控制着函数Fσx对l0范数的近似程度，即σ越小，函数越趋近于l0范数，但同时函数存在的局部极值也越多，则Fσx在逼近l0范数的过程中，易陷入局部极值，极大地增加了对函数全局极值的求解难度。为了解决该问题，本文将σ取为一组逐次下降的序列σ1>σ2>,…>σJ，其中σJ为一个接近于零的极小正值。然后利用修正牛顿法将σi1≤i≤J对应的式(13)进行求解，使得算法能够逐渐逼近全局最大值。

1.2 利用修正牛顿法求解修正函数所表示的稀疏问题

SL0算法通常利用最速下降法求解高斯函数的全局最大值，虽然最速下降法步骤简单，且每次计算函数极大值时的迭代量很小，但是在搜寻函数全局最大值的过程中会出现“锯齿效应”[13]，从而对SL0算法的重构精度产生不利影响。针对此问题，本文利用修正牛顿法[15]求解式(11)，从而提高了稀疏信号的重构精度。对于函数Fσ(x)，其牛顿方向为

d=-Δ2Fσ(x)-1ΔFσ(x)

(12)

式中

(13)

(14)

其中

在计算出函数Fσ(x)的牛顿方向d之后，其中矩阵Δ2Fσ(x)是Hessen矩阵，该矩阵不满足正定条件，进而不能保证牛顿方向d为下降方向。为保证d为下降方向，文中对式(14)中的对角元素进行修正，从而构造一个新矩阵H来代替牛顿方向d中的Δ2Fσ(x)矩阵。新矩阵H的表达式为

H=Δ2Fσ(x)+ψ

(15)

式中：ψ为一个对角矩阵，为方便计算，本文将其对角元素ψi取为

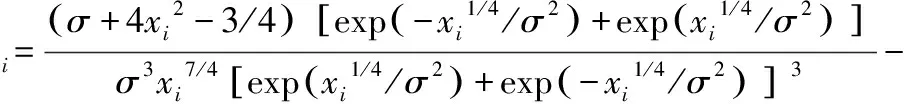
(16)

由此可得，H中第i个对角线上的元素为

(17)

由上式可知，修正后的新矩阵H满足正定条件，利用新矩阵H代替牛顿方向d中的Δ2Fσ(x)矩阵，以保证牛顿方向d为下降方向，即改进后的修正牛顿方向为

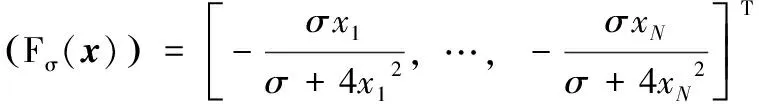
(18)

本文算法步骤总结如下：

步骤1 初始化：

步骤2 算法迭代：

forj=1,2,…,J

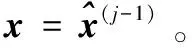
(2) 在修正牛顿方向上逐次搜寻函数Fσ(x)的全局最小值，并将该最小值投影到可行集上。

forl=1,2,…,L

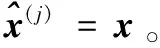
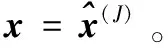
2 仿真结果及分析

为验证本文算法的稀疏重构性能，本节设计了几组SL0算法、NSL0算法、ASL0算法和本文算法的对比实验。在本文仿真中，稀疏源信号是通过伯努立-高斯模型[16]随机生成，该模型为

xi～p·N0,δon+1-p·N0,δoff

(19)

其中，p为源信号中出现大的非零量的概率；N(0,δ)为高斯加性白噪声，其均值为零，方差为δ;δon和δoff分别是构成源信号的较大非零系数和较小非零系数。设置δoff≪δon，且p≪1，以保证源信号的稀疏性。在本文仿真中，y∈M×1为随机采样矩阵，x∈N×1为稀疏源信号矩阵，D∈M×N为感知矩阵。对于y=Dx，在已知y和D的情况下，分别利用SL0算法、NSL0算法、ASL0算法以及本文算法对稀疏源信号进行重构。用于产生稀疏源信号的模型中参数设置分别为M=1000,N=400,δon=1,δoff=10-3,p=0.1；在SL0算法、NSL0算法、ASL0算法和本文算法中，设置σJ=0.001,ρ=0.7，内循环次数L=5。

定义信噪比为

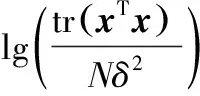
(20)

式中：tr(·)表示对矩阵进行求迹。本文采用重构信噪比和重构误差来评价各算法的重构性能，重构信噪比定义为

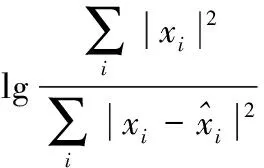
(21)

(22)

仿真内容一：不同算法对稀疏信号重构的实验

图2是原始信号以及利用各算法获得的重构信号对比图。源信号稀疏度表示信号矩阵中非零元素的个数。本次仿真中，取稀疏度K=100，信噪比SNR=30 dB。本文算法采用了一种修正近似双曲正切函数来逼近l0范数，提高了平滑函数对l0范数的近似程度，由图2可知，相比于SL0算法，NSL0算法和ASL0算法，本文算法重构出的稀疏信号最接近于原始源信号。

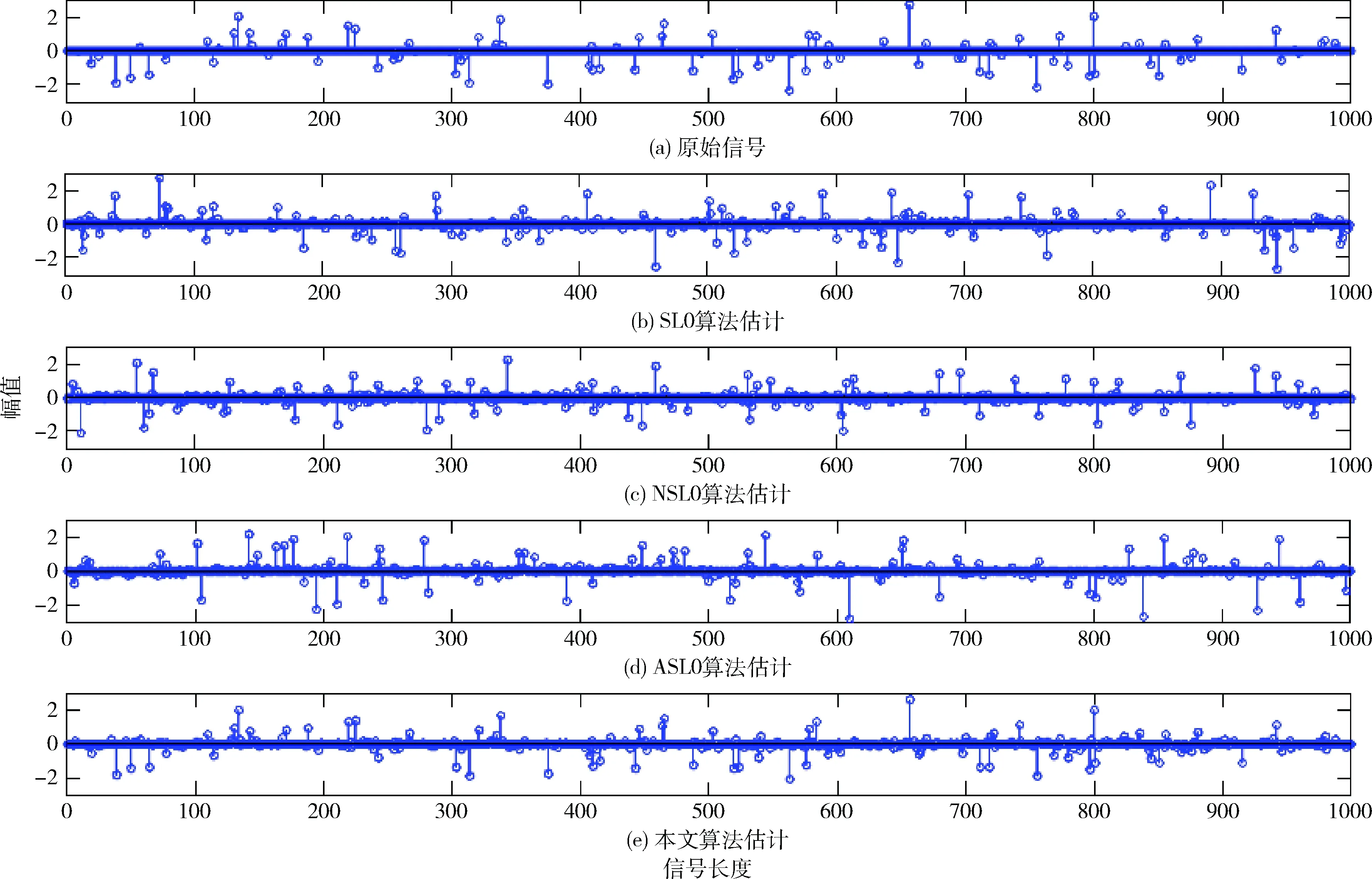
图2 原始稀疏信号以及利用各算法获得的重构信号

仿真内容二：各算法的重构性能与信噪比的关系

图3和图4分别为4种算法的重构信噪比和重构误差与信噪比的变化关系。设信噪比变化范围为20 dB～40 dB，信号稀疏度K=100，进行200次仿真实验。由图3和图4可知，由于在NSL0算法和ASL0算法中所采用的近似双曲正切函数对l0范数的近似程度优于高斯函数，而且利用了修正牛顿法来求解平滑函数的极值问题，避免了最速下降法在迭代过程中产生的“锯齿效应”，因此NSL0算法和ASL0算法的重构信噪比要高于SL0算法，而重构误差要低于SL0算法。本文算法采用了一种修正的近似双曲正切函数，其近似l0范数的程度要优于NSL0算法和ASL0算法中的平滑函数，由图3和图4可知，本文算法的重构性能最好。

图3 不同算法的重构信噪比与信噪比的变化关系

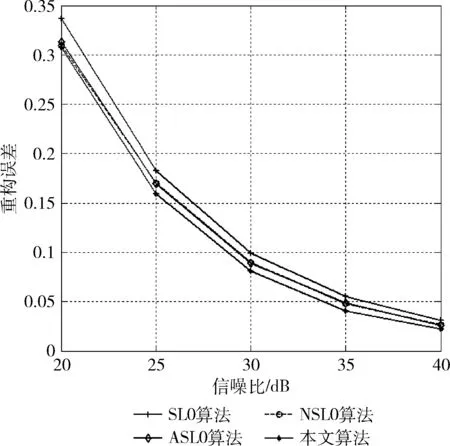
图4 不同算法的重构误差与信噪比的变化关系

仿真内容三：各算法的重构性能与稀疏度之间的变化关系

图5和图6分别为各算法的重构信噪比和重构误差与稀疏度的变化关系。假设稀疏度K的变化范围为20～100，信噪比为30 dB。由图5和图6可知，本文算法在不同信号稀疏度下其重构性能始终要优于SL0算法、NSL0算法和ASL0算法。

图5 不同算法的重构信噪比与稀疏度的变化关系

图6 不同算法的重构误差与稀疏度的变化关系

3 结束语

SL0算法一般采用高斯函数作为平滑函数来近似l0范数，但是高斯函数对l0范数的近似程度不够理想，并且利用最速下降法求解函数极值问题时会产生“锯齿效应”，从而导致该算法的稀疏信号重构性能较差。本文提出一种基于修正近似双曲正切函数的平滑l0范数算法，该算法采用一种修正近似双曲正切函数来逼近l0范数，同时利用牛顿法求解该函数的极值问题，从而实现了稀疏信号的高精度重构。数值仿真实验结果表明，与其它算法相比，本文算法的稀疏信号重构性能最优。