落叶松抗弯弹性模量的细观尺度建模方法1)
于慧伶 潘屾 张怡卓
(东北林业大学,哈尔滨,150040)
木材力学性质是木材加工利用的重要指标[1]。传统研究方法是基于假设其内部均匀的条件下求取连续介质的力学性质,其目的是选用适当的本构关系来描述材料对外部作用的响应[2]。但是,木材是一种复杂的天然纤维增强复合非匀质材料,在木材中存在不同层次的复合作用。在宏观结构上,木材可以视为由不同的生长轮层合而成;在微观上,细胞壁是木材的实际承载结构[3],在受力过程中,细胞壁的形态会发生迁移和改变,直至微纤丝断裂[4]。因此,由木材结构的细胞特点出发,通过计算各生长轮早晚材细胞参数及其排列变化,可以较为客观地反映木材力学性能。
国内外许多学者很早就将木材的力学变形与木材内部结构的显微观察结合起来研究,同时,数字图像处理技术也逐渐应用于木材微观结构分析。Charles利用当时的图像处理技术测量了木材细胞率、纤维长度、细胞腔面积[5];岩切一树用图像的累计处理方法测量了细胞壁厚度。Llic和Hillis对按树木质部细胞管腔面积以及不同细胞类型所占面积比例等特征实现了较为简单的量化处理,利用图像处理的方法对操作区域内任两点间产生的应变进行计算并得出剪切力应变和泊松比[6]。刘一星等采用计算机图像处理技术对火炬松管胞形态和木材物理力学特征进行了分析,得到材性指标的变异规律[7]。曹军等对木材横纹压缩过程的解剖特征进行了研究,计算出早晚材细胞的相关参数,提取了细胞边缘的形态特征[8]。殷亚方等对毛白杨枝条形成层细胞与其衍生木质部细胞解剖特征进行了研究,并得出了其在形成层活动期内的变化情况[9]。
1 材料与方法
1.1 材料
落叶松(Larixgmelinii)松科落叶松属的落叶乔木,是中国东北、内蒙古林区的主要森林组成树种,重而坚实、抗压及抗弯曲的强度大,是电杆、枕木、桥梁、矿柱、车辆、建筑等领域的优良用材。
试验所需的落叶松试件采自黑龙江省五常市林业局冲河林场。在落叶松人工林内,选取树龄20 a,伐倒并标记树木生长方向,在树的胸高1.3 m往上截取长度为1 m的木段。按照GB1936—1980《木材抗弯弹性模量试验方法》的规定进行。制备试样,尺寸为300 mm×20 mm×20 mm,支撑点跨度为240 mm,总计10个。
1.2 细胞图像采集与预处理
采用日本基恩士公司生产的VHX-2000系列超景深三维显微系统进行图像采集,采用仪器自带的光源对事件进行照射采集图像,设备如图1所示。

图1 VHX-2000数码显微镜
在采集细胞壁与细胞腔的过程中,由于切片的薄厚不均会造成采样得到原始图片存在亮度不均、噪点或局部细节不够清晰等问题,需要对原始图片进行预处理以方便后续处理,并要对采集的图像进行二值化运算。图2为木材细胞采集原始图像与二值化处理后图像。图像反映出落叶松的显微构造组成简单、排列整齐,材质比较均匀。
1.3 细胞图像数据计算
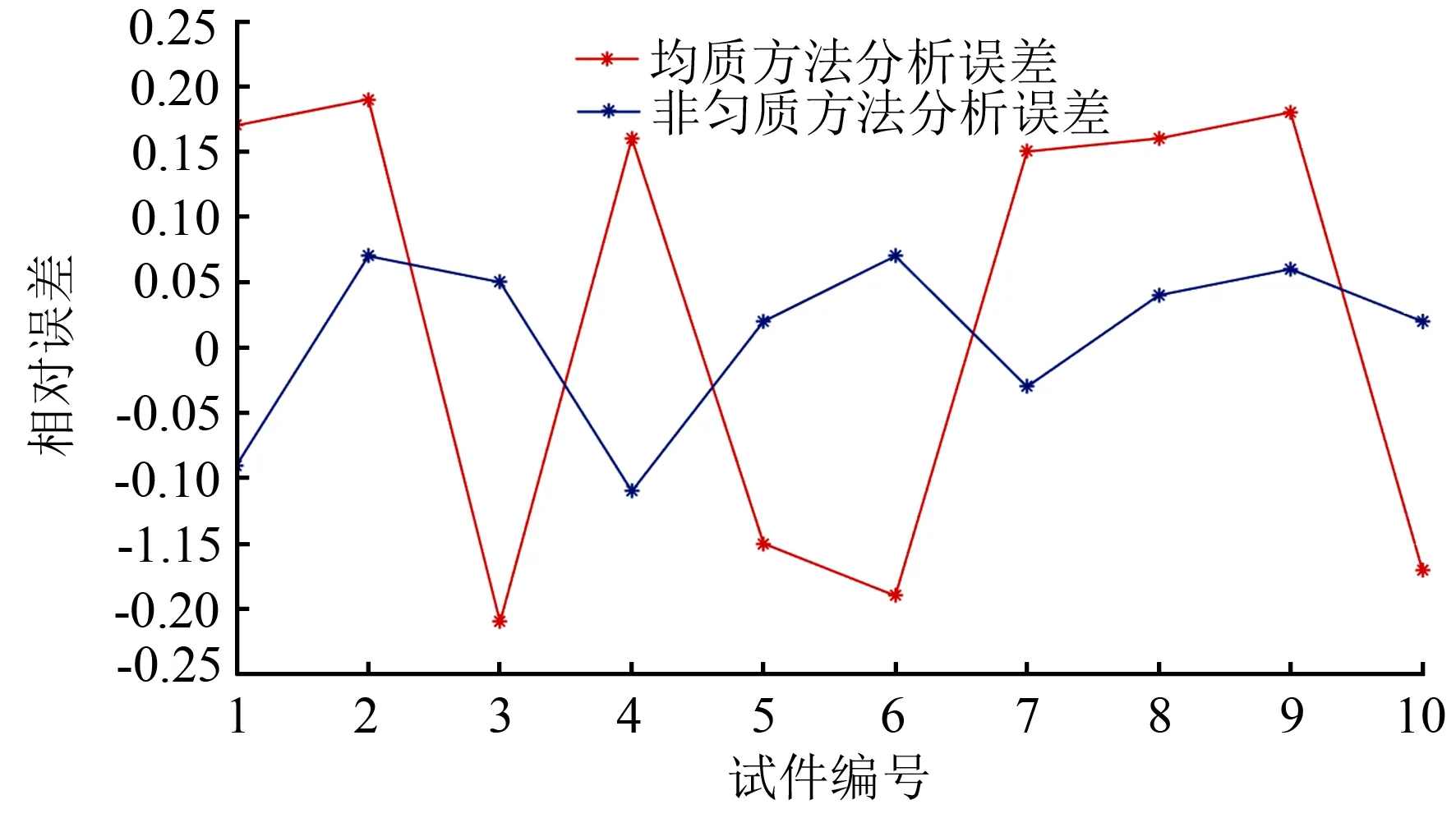
落叶松的细胞形状如图3所示,可近似不规则的六边形。其中,Wr是径向宽度;Wt1和Wt2是切向宽度;t是细胞壁的厚度;偏心率为e,e的范围为0 图2 细胞原始图像及二值化效果图 图3 细胞结构示意图 胞壁率是细胞壁面积占整个细胞面积的比率,其计算形式如下: (1) 式中:s为胞壁率;AW是细胞壁的截面积;At是包括内腔的细胞的全部面积。 根据文献[10],细胞的平均密度可以通过胞壁率和细胞壁的体密度计算,其计算公式如下: 选择榆林市周边的榆横矿区和榆神矿区为研究对象。榆林市矿区地处中纬度干旱半干旱地区。降水量小且时空分布不均匀是大气降水的主要特征[8]。根据气象资料分析,多年平均降水量为392 mm,主要集中在每年的6、7、8、9四个月,占全年总降水量的75%,多年平均蒸发量为2 200 mm。榆林市矿区为沙漠风沙滩区,煤炭未大量开发前,含水层以上更新统萨拉乌苏组中细砂为主(以下称萨拉乌苏组潜水),为当地居民饮用和灌溉的主要水源[2]。潜水交替循环积极,水质较好,其地下水化学类型主要为HCO3-Ca·Na或HCO3-Ca·Mg型水,矿化度一般小于500 mg/L。 ρi=s×ρ0。 (2) 式中:ρi为第i生长轮早材、晚材的密度,细胞壁的体密度取ρ0=1 500 kg/m3。 根据文献[11],对于第i生长轮的早材与晚材的弹性模量采取以密度为单一变量的预测模型: Ei=0.442ρi-4.992。 (3) 式中:Ei为第i层生长轮早材或晚材的弹性模量;ρi为第i层生长轮早材或晚材的密度。 木材的宏观结构可看作是由多个生长轮构成的,其中每一个生长轮都是由早材和晚材层合而成,早材和晚材又都由细胞构成。木材中存在几种不同层次的复合作用,因此,复合材料力学应是木材宏观机械性能研究的首要工具。研究宏观的外力在生长轮间分布和传递的理论,即要研究宏观组织受力与单层结构间的本构关系,同时还要研究层合板的强度理论,对木材进行强度分析,最后用木材顺纹抗弯强度试验加以验证。 这里假设生长轮为基本单元,木材宏观结构就可以用生长轮为基本单元进行建模。而微观结构中,每一个生长轮内的早材与晚材的细胞力学性质都由公式(1)、(2)、(3)计算出。用UG三维建模软件根据试件截面图像的生长轮纹理的实际尺寸进行三维立体建模,并通过通用接口导入到Ansysworkbench中。模型由杨氏弹性模量、泊松比、材料密度3个参数来确定物理性质,划分网格创建有限元模型。由于落叶松是较为规律的长方体,网格自动生成,划分情况如图4所示。 图4 划分网格后的有限元模型 对试件模型施加约束条件,包括边界条件、初始条件,在材料两侧施加固定支撑,施加载荷,设置载荷及求解控制选项。图5为施加约束后的模型。 图5 对模型施加约束 通过有限元软件查看并分析、检验求解的结果。计算结果可以通过颜色云图、等值线图显示(如图6所示),也可以通过曲线来描述数值的变化,或通过数据文件直接查看。 图6 木材结构位移图 表1为10个试件通过力学性能测试得到的弹性模量值与采用非匀质材料理论预测的弹性模量值的对比。实验得到的相对误差为2%~11%,其平均误差为5.7%。 表1 ANSYS计算值与试件弹性模量比较 运用匀质方法求落叶松顺纹抗弯弹性模量时,认为落叶松由管胞为单元构成的匀质材料。管胞在长轴方向上首尾相接,在径向和弦向以相同形态细胞排列形成弹性模量。 表2为10个试件通过力学性能测试得到的弹性模量与匀质方法求得的弹性模量值的对比。实验得到的相对误差为15%~21%,其平均误差为17.3%。 表2 匀质方法分析值与弹性模量比较 图7为非匀质方法预测试件弹性模量的误差与匀质方法求得试件的弹性模量误差的对比,可以看出采用层合材料理论的非匀质方法预测试件的弹性模量更为准确。 图7 两种方法误差对比 应用匀质材料建模方法预测针叶材力学性能时,首先利用管胞细胞模型推导出管胞纵向弹性模量,然后根据管胞细胞排列,结合弹性体串并联的特性计算木材试件宏观纵向弹性模量。这种方法在宏观上可以完成弹性模量的估算,但是,由于木材具有各向异性的特点,这种匀质材料建模方法在精度上存在较大误差。实验数据表明,该方法的相对误差为15%~21%,平均误差为17.3%。 本研究从木材细胞尺度上对落叶松试件的力学性能进行建模,将其理想成由不同壳型材质构成。通过早材和晚材细胞数据得到不同生长轮内的密度,进而计算出不同壳体的弹性模量,最后,应用有限元力学模型构建出落叶松宏观弹性力学模型。这种方法考虑了木材非匀质特性,并将这种非匀质特点分散到各生长轮层中,通过生长轮内的细胞变化完成宏观力学特性预测,预测值与真实值更加吻合。实验数据表明,该方法的相对误差在2%~11%范围内,平均误差为5.7%。该方法可以为终端客户提供更科学、准确的落叶松力学预测数据以及可视化的力学响应效果。

2 应用层合理论对落叶松弹性模量求解
2.1 落叶松三维有限元模型建立




2.2 应用匀质方法对弹性模量计算

3 结果与分析

