求解多峰函数的聚类布谷鸟算法的研究

汪峰坤，张婷婷

安徽机电职业技术学院信息工程系，芜湖，241000

多峰函数的求解是指求解函数的多个全局或局部的最优解，在工程应用中被广泛使用[1,2]。通过求解的多个局部最优解，为使用者提供更多的决策选择。当前针对多峰函数求解和优化常用的方法有基于小生境的遗传算法、基于引路蜂的人工蜂群算法和多种群的粒子群算法等[3-5]。

数据聚类分析是广泛用于数据挖掘、模式识别和机器学习等领域的一类重要算法。聚类分析算法与遗传算法、粒子群算法等智能算法相结合，通过聚类将搜索重点放到各聚类中心附近，可以快速收敛到各聚类的最优值，如果聚类较为合理，则可以求解多峰函数的解[6,7]。

布谷鸟算法是一种常用的函数寻优算法，以其快速的收敛和较大的搜索范围，广泛应用于最优解求解中。当前尚未有将布谷鸟算法用于多峰函数求解方面的研究。本文提出了基于最大最小距离法(Max-Min Distance)的鸟巢快速聚类，针对每个聚类使用布谷鸟算法搜索，得到每个聚类的局部最优值的多峰函数求解方法。

1 布谷鸟算法基本算法

杨新社等2009年提出了针对函数最优值求解的布谷鸟算法[8]。布谷鸟算法是模拟自然界中布谷鸟寄生育雏的行为来求解函数最优值问题。布谷鸟算法核心思路有：使用Lèvy飞行进行鸟巢新址的选择，使用偏好随机游走策略进行随机大范围跳转。

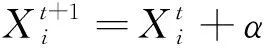
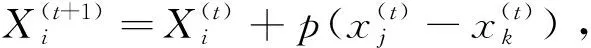
2 改进算法

2.1 聚类方法的改进

聚类是指把性质相近的对象分在一起作为同一种类别。大部分聚类算法基于欧几里得距离来决定聚类。基于这种距离的算法可以发现球形簇或相近距离的簇。聚类算法判断聚类优劣性的通用原则是：类内距离最小，类间距离最大[9]。

对聚类中心判断的通用方法是：

(1)以适应度最小的值作为第一个聚类中心。

(2)计算其余结点到当前所有已知的聚类中心的距离之和。

(3)以距离最大的值作为新的聚类中心。

(4)重复(2)-(4)步骤，直到找到所有的聚类中心。

经过理论证明和实验仿真，此方法并不能找到最好的聚类中心。

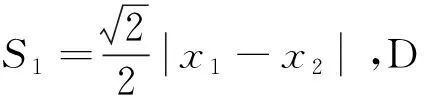
本文提出了计算聚类中心的新算法，名称为最大最小距离法,求解聚类中心的过程如下：

(1)以适应度最小的值作为第一个聚类中心。

(2)计算其余结点距已知聚类中心的距离，选择最小的距离作为此结点到已知聚类中心的距离值。

(3)查找到聚类中心的最大距离值的结点，以此结点作为新的聚类中心。

(4)重复(2)-(3)步骤，直到找到所有的聚类中心。

设鸟巢总数为N，要求峰数为K，则最大最小距离法求解聚类中心的时间复杂度为：O(KN)。

2.2 各聚类的布谷鸟算法的改进

对于各聚类中鸟巢的最优值求解，本文采用基于聚类精英策略的小生境布谷鸟算法，流程如下：

(1)查找到类中最优鸟巢(适应度最小)。

(2)循环遍历聚类中其他鸟巢，由原来的鸟巢生成新鸟巢。

(3)各鸟巢的Lèvy飞行中的基本步长值定义为当前鸟巢与当前聚类中最优鸟巢之间的距离。

(4)使用随机游走策略生成新的鸟巢。

对于多峰函数解的搜索过程，本文针对布谷鸟算法改进如下：

使用基于各聚类的精英策略，保留了各聚类中最优解，最优解不进行Lèvy飞行，从而保证进化过程中，各聚类最优解不减少。对于各聚类内部，使用了小生境和向最优靠近策略，使各类中鸟巢在最优值附近进行Lèvy飞行搜索，增加局部收敛速度。通过随机游走策略增加搜索范围。

2.3 算法总体流程

本文提出针对多峰问题求解的整体流程如下：

(1)随机生成所有鸟巢，计算各鸟巢的适应度。

(2)通过最大最小算法求出所有的聚类中心。

(3)计算所有鸟巢距各聚类中心的距离，将各鸟巢归类到距离最近的聚类中。

(4)使用改进的布谷鸟算法对各聚类进行搜索最优值。

(5)循环(2)-(4)步骤，直到满足退出条件。

(6)输出各聚类的最优值。

3 算法实验与分析

3.1 实验采用的多峰函数

本文求解多峰函数的最小值，参考其他相关文献，选择仿真的多峰函数如下：

(1)函数f1：

f1(x)=-sin6(5π(x0.75-0.05))，函数定义域为：[0,1]。存在着5个非均匀等值分布的峰，峰值为-1，自变量为：0.08,0.247,0.451,0.681和0.934。

(2)函数f2：

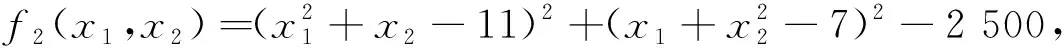
(3)函数f3：

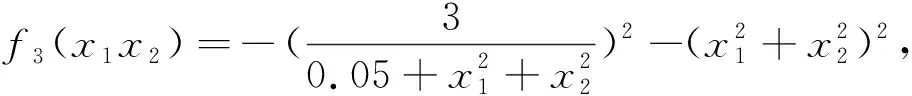
3.2 算法性能分析

算法参数设置为：鸟巢个数N=100，迭代次数M=100,K为函数实际峰值个数，根据函数特点取值。运行10次，取平均值作为计算结果。

3.2.1 选择聚类中心算法

以函数f1为例进行实验仿真，下图为某次初始化后鸟巢分布和两种算法求解的5个聚类中心，结果如图1。

由图1可知，使用最大距离算法求得的聚类中心远没有本文提出的最大最小距离算法计算的聚类中心分布均匀。

3.2.2 不同多峰函数求解

本文使用峰值误差比率和距离误差比率来衡量算法的准确程度。峰值误差比率定义为所求出的所有峰值与真实峰值之间差距的平均值与真实峰值平均值的比值的绝对值。距离误差值定义为所求出的所有峰值与真实峰值的坐标之间距离的平均值。峰值误差比率和距离误差值为非负数，越小越好。

由表1可得，本文所提出的算法可以搜索到所有峰值。函数f1较简单，峰值误差比率和距离误差值效果都非常好。函数f3较为复杂，本算法准确地找到4个局部最优解，全局最优解有一定的误差，也在可接受范围内。由于函数f3对自变量参数比较敏感，所以距离误差值小于函数f2时，函数f3峰值误差比率仍然比函数f2大。

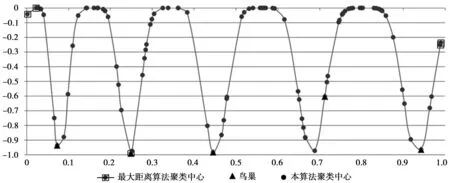
图1 最大距离算法和最大最小距离算法求解聚类中心的比较

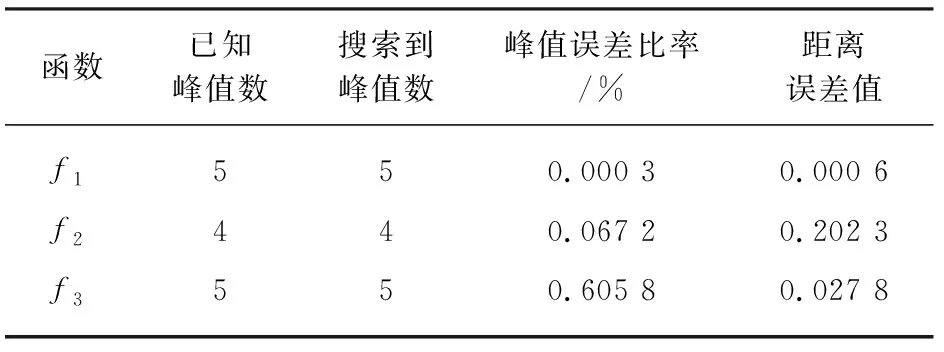
表1 不同多峰函数求解

3.2.3 算法收敛速度

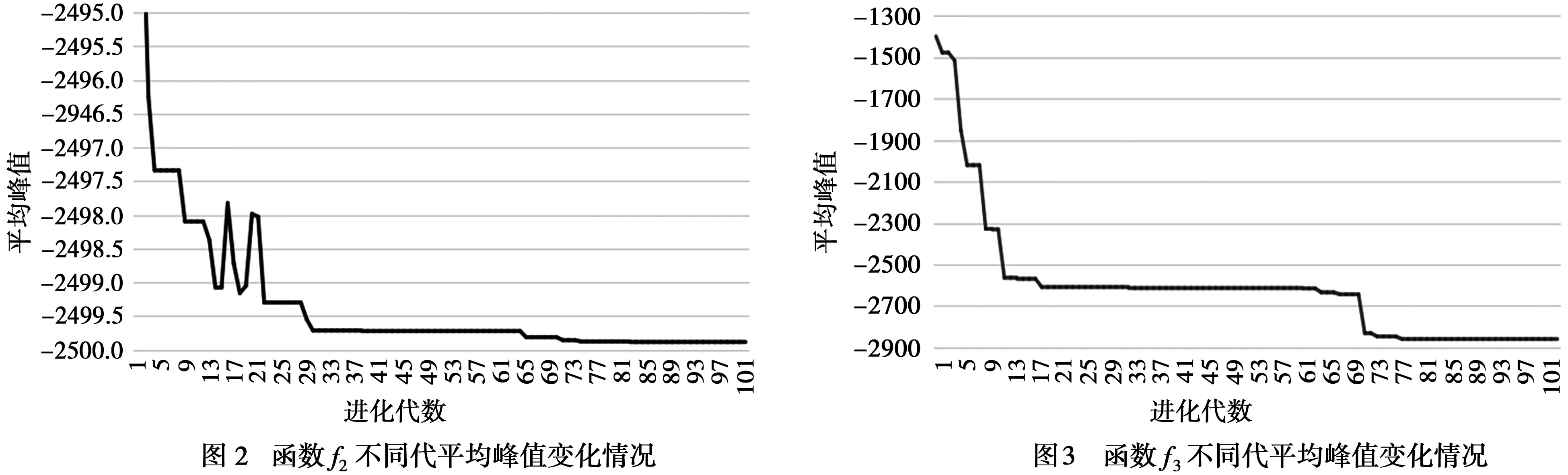
图2和图3为从第1代到第100代函数f2和函数f3每一代求解的所有峰值的平均值。由图2和图3可知，本算法在前期快速收敛到函数各峰值附近，在后期收敛速度变慢，但仍有可能找到更好的解。在搜索过程上，由于Lèvy飞行和随机游走策略有一定的随机性，可能会小概率出现平均峰值变坏的情况，如图2中间13-20代，但不影响总体变化趋势。

4 结 语

本文提出求解多峰函数的聚类布谷鸟算法，针对常用的最大距离法的不足，提出了效果更好的最大最小距离方法，该方法求出的聚类中心分布更加均匀。对于各聚类中的鸟巢使用布谷鸟算法进行局部寻优，布谷鸟算法可以快速收敛到局部最优解，并且利用Lèvy飞行的重尾特性和小概率的偏好随机游动，可以提高搜索的范围。通过实验仿真表明，本算法有一定的实用价值。