数学思维在中学生物学教学中的渗透

汤华利

（四川省成都市第十八中学校，四川 成都）

著名科学家伽利略认为：“自然的语言就是数学，要表达自然的运动规律，应当使用数学和实验数据。”在中学生物学教学中，如何充分应用数学这个工具，笔者尝试了运用“集合思想”“函数思想”“因式分解思想”“数形结合思想”等数学思想，采用“渗透式”教学法，将一些生物学知识用数学语言描述，将一些生物学基本概念、基本规律进行数学抽象，将一些生物学中的生理过程具体化、简单化。

一、运用因式分解思想，将复杂的生物学问题简单化

因式分解是把一个多项式在一个范围化为几个整式的积的形式。在遗传学中，基因自由组合问题，就是由几个基因分离问题利用“乘法原理”组合的结果。因此，求解复杂的基因自由组合问题，即可利用因式分解思想，将其转化为几个基因分离问题的乘积。

分析该类问题时，首先根据分离定律的原理，找出要分解成的因式；其次根据自由组合问题的结果，进行因式分解；最后根据各因式对应的分离定律结论进行组合，从而得出相应的自由组合问题的结论。

例1.与玉米籽粒颜色相关物质的合成途径如图1所示，基因M、N和E及它们的等位基因依次分布在第1、2、5号染色体上，现有一紫色籽粒玉米植株自交，后代籽粒的性状分离比为紫色∶红色∶白色=9∶3∶4，则该植株的基因型可能为 （ ）

图1

A.MMNNEE B.MmNNEe C.MmNnEE D.MmNnEe

分析：（1）根据基因对性状的控制流程图，写出各性状的基因型通式：紫色；红色白色或

（2）根据分离定律原理，找出要分解成的因式：

亲代基因型 子代表现型显性∶隐性 显性性状比例 隐性性状比例Aa×Aa 3∶1 3/4 1/4 Aa×aa 1∶1 1/2 1/2 AA× ？ 1∶0 1 0 Aa×aa 0∶1 0 1

（3）根据题干中，一色紫子粒玉米自交子代中红色子粒（M N ee）占 3/16，进行因式分解：M N ee=3/16=3/4×1×1/4 或者M N ee=3/16=1×3/4×1/4。

（4）根据分离定律原理，及子代红色子粒性状分离比的因式分解结果，确定亲代紫色子粒玉米的基因型为MmNNEe或者MMNnEe。

二、运用数形结合思想，将抽象的生物学问题具体化

图形语言是最具体和形象的一种数学语言，在生物学中，将一些抽象的、组合方式多样的、逻辑性强的生理过程，用图形描绘出来，从而找出一定的数学规律。

分析该类问题时，首先根据相关生理过程，绘制相应生理过程图，然后根据图形找出要求解问题的数学规律。

例2.将DNA分子双链用3H标记的豌豆（2n=24）根尖移入普通培养液（不含放射性元素）中，让细胞连续分裂。根据如图2所示判断在普通培养液中的第四次分裂中期，细胞中染色体标记情况依次是（ ）

A.24个b

B.a+c=24个，但a和c数目不确定

C.12个b，12个 c

D.b+c=24个，但b和c数目不确定

图2

分析：（1）根据有丝分裂过程染色体的行为变化和DNA的半保留复制特点，绘制一个细胞中部分染色体在两次有丝分裂过程中的变化图，如图3：

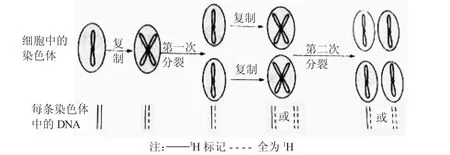
图3

（2）根据图形，找出细胞分裂中期染色体标记情况规律：第一次分裂中期染色体标记为24个a；第二次分裂中期染色体标记为24个b；第二次结束的子细胞中染色体标记为25种情况：24个都未标记；23个未标记+1个被标记……24个都被标记。

（3）根据得出的规律，推出第三次及以后分裂中期染色体标记情况都有25种：24个c；23个c+1个b……24个b

数学思维在中学生物学教学中的渗透，是多元化教学手段运用的结果，它既可提高教师的自身素质，也是培养创新性复合型人才的重要途径。