基于降低流固耦合振动的罗茨风机壳体结构优化*
周志海,袁泽峰
(长沙理工大学 汽车与机械工程学院,湖南 长沙 410114)
0 引言
罗茨风机为容积式风机,由于其结构紧凑、精度高、体积小、寿命长等优点被广泛应用于建材、电力、冶炼、化工、矿山、港口、水产养殖、污水处理等各种气体输送领域[1]。但罗茨风机工作中产生的振动一直是影响风机稳定运行的不利因素,而引起罗茨鼓风机振动的因素较多,如地脚螺栓松动、联轴器不合格、风机基础刚度差、同步齿轮啮合间隙大、转子不平衡以及其他轴系零件松动等[2]。除此之外,由于罗茨鼓风机自身的工作特点,叶轮转子旋转排气是不连续的,因此风机运转过程中将不可避免地产生随工作转速变化的气流脉动[3-4],受此激振力作用,风机将产生不同大小的振动和噪声。
近年来,随着对各类机械结构动态特性要求的提高,结构动力修改问题越来越受到重视,特别是结构修改的逆问题一直是结构动力学极为活跃的研究方向[5]。风机壳体是罗茨风机的主要部件,为了提高罗茨风机运行的稳定性,改善风机在气流脉动下的动态性能,本文针对长沙鼓风机厂有限责任公司生产的S31型罗茨鼓风机机壳,结合机壳模态分析结果及风机气体压力脉动分析结果对其进行结构动力修改,以减小风机壳体在气体压力脉动激励下的耦合共振。
1 罗茨鼓风机机壳优化目标分析
在罗茨鼓风机机壳有限元模型各个法兰连接处施加螺栓预紧力,并添加标准重力,利用ANSYS环境下的Block Lanczos求解方法求得机壳前6阶固有频率和振型特征(由于风机在工作情况下主要产生低频振动,而第7阶固有频率值已接近1 000 Hz,更高阶的固有频率及振型将不具有分析价值,分析前6阶模态足够),如表1所示。

表1 机壳的前6阶固有频率和振型特征
由表1可知:①机壳前两阶固有频率之差较小,容易发生共振效应;②罗茨风机转速一般为490 r/min~3 000 r/min,旋转噪声基频为49 Hz~300 Hz,使风机噪声呈现低频特征[6]。脉动激励频率fi的计算公式为[7]:
(1)
其中:n为叶轮转子转速;z为叶轮叶片数;i为基频倍数,i=1,2,…,n。
实际工况下S31鼓风机叶轮转子有3种稳定工作转速:1 450 r/min、2 100 r/min、2 800 r/min。长沙鼓风机厂S31型罗茨鼓风机叶轮为一对三叶转子,故叶轮叶片数为6。
由式(1)可计算得到各转速下叶轮转子产生的气体压力脉动激励频率,如表2所示。

表2 各转速下叶轮转子产生的气体压力脉动激励频率
表2中,1倍脉动频率即为实际工况下叶轮转子产生的脉动频率,为保险起见,列出2倍脉动频率下可能产生的脉动频率,作为分析参考。机壳第2阶、第4阶振型的固有频率分别为148.75 Hz、420.39 Hz,与表2中1 450 r/min转速下1倍脉动频率(145 Hz)和2 100 r/min转速下2倍脉动频率(420 Hz)接近,若气体压力脉动所产生的激励较大,则风机在这两种情况下运行有可能产生强烈振动和噪声,因此需要对第2阶、第4阶固有频率进行修改,以减小耦合共振。
2 结构动力修改
2.1 灵敏度分析
由于机壳壳体三维模型结构复杂、曲面较多,灵敏度分析有利于找出敏感设计点,节约设计成本,减少设计的盲目性。
结构参数对频率的一阶灵敏度可表示为[8]:
(2)
其中:ωr为结构第r阶固有频率;pm为结构设计参数或设计变量,主要指结构尺寸、几何形状、质量、刚度及阻尼元素等;Φr为结构第r阶振型;M为结构的质量矩阵;K为结构的刚度矩阵。
若用质量元素mij代替式(2)中的pm,则可以求得质量对频率的灵敏度表达式为:
(3)
其中:Ψir、Ψjr为结构第r阶振型列向量的第i、j个元素。
为直观分析非关键部位的几何尺寸对机壳各阶固有频率的影响,改变非关键因素的几何尺寸,可以改变机壳有限元模型的质量矩阵,设计变量取机壳中部两侧加强筋厚度、进出气口端法兰面厚度以及前后墙板法兰面厚度(如图1所示),分析其对机壳的灵敏度。设计变量对机壳的前6阶灵敏度分析结果如表3所示。
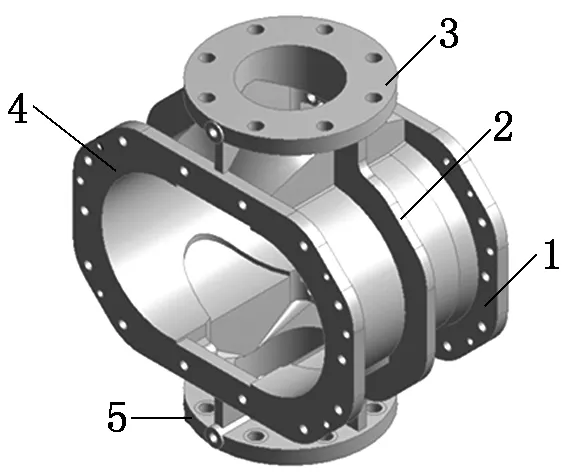
1-前墙板法兰面;2-加强筋;3-进气口法兰面;4-后墙板法兰面;5-出气口法兰面
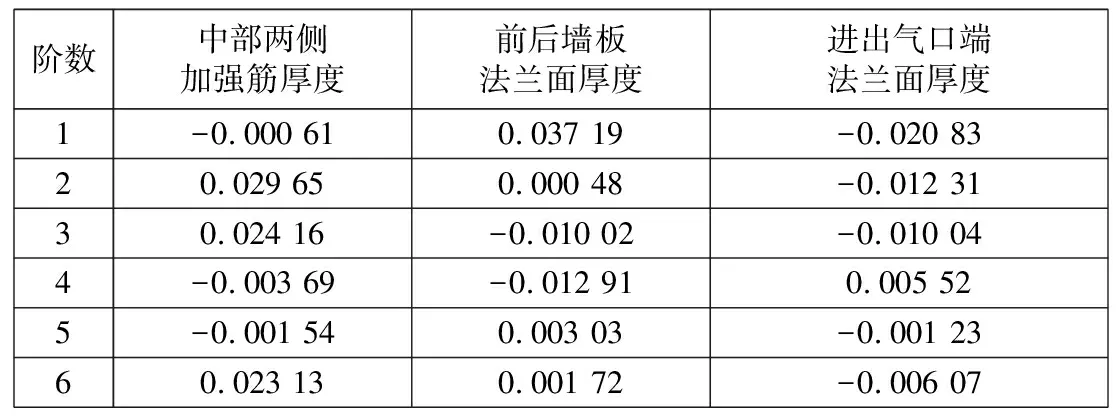
表3 设计变量对机壳的前6阶灵敏度分析结果 (Hz·kg-1)
由表3可知:中部两侧加强筋厚度的增大对第1阶、第4阶、第5阶机壳固有频率影响较小,而对第2阶、第3阶、第6阶机壳固有频率有较大正效应;进出气口端法兰面厚度的增大对第1阶、第2阶、第3阶、第5阶、第6阶机壳固有频率均有负效应,对第4阶机壳固有频率有正效应;前后墙板法兰面厚度的增大对第2阶、第5阶、第6阶机壳固有频率影响较小,对第1阶机壳固有频率有较大正效应,相对其他两个结构设计变量其对第4阶机壳固有频率有较大负效应。
2.2 机壳结构优化的设计方法
本次采取试验设计方法(Design of Experiment,简称DOE)进行优化设计,具体采用的是DOE方法中较为常用的中心复合设计(Central Composite Design)[9-10],并根据优化设计的三个基本要素确定设计变量、约束条件和优化目标,借助ANSYS Design Exporation工具完成优化。
2.3 数学模型及响应面模型分析
结合机壳固有频率灵敏度分析结果,得到机壳结构优化数学模型:
优化目标:maxF2(X),minF3(X).
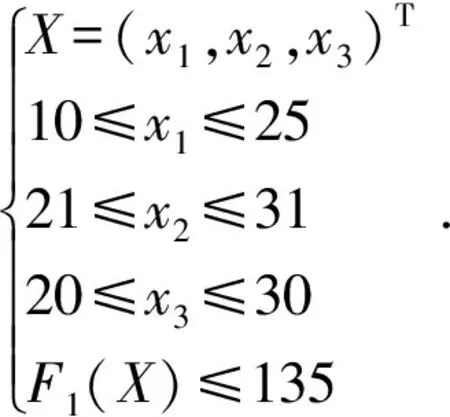
(4)
其中:x1为中部两侧加强筋厚度;x2为进出气口端法兰面厚度;x3为前后墙板法兰面厚度;F1(X)为机壳第1阶固有频率;F2(X)为机壳第2阶固有频率;F3(X)为机壳第4阶固有频率。
根据式(4)所确定的约束范围,利用中心复合设计原理,在参数的设计空间内确定了15个样本点,得到的有限元试验结果如表4所示。
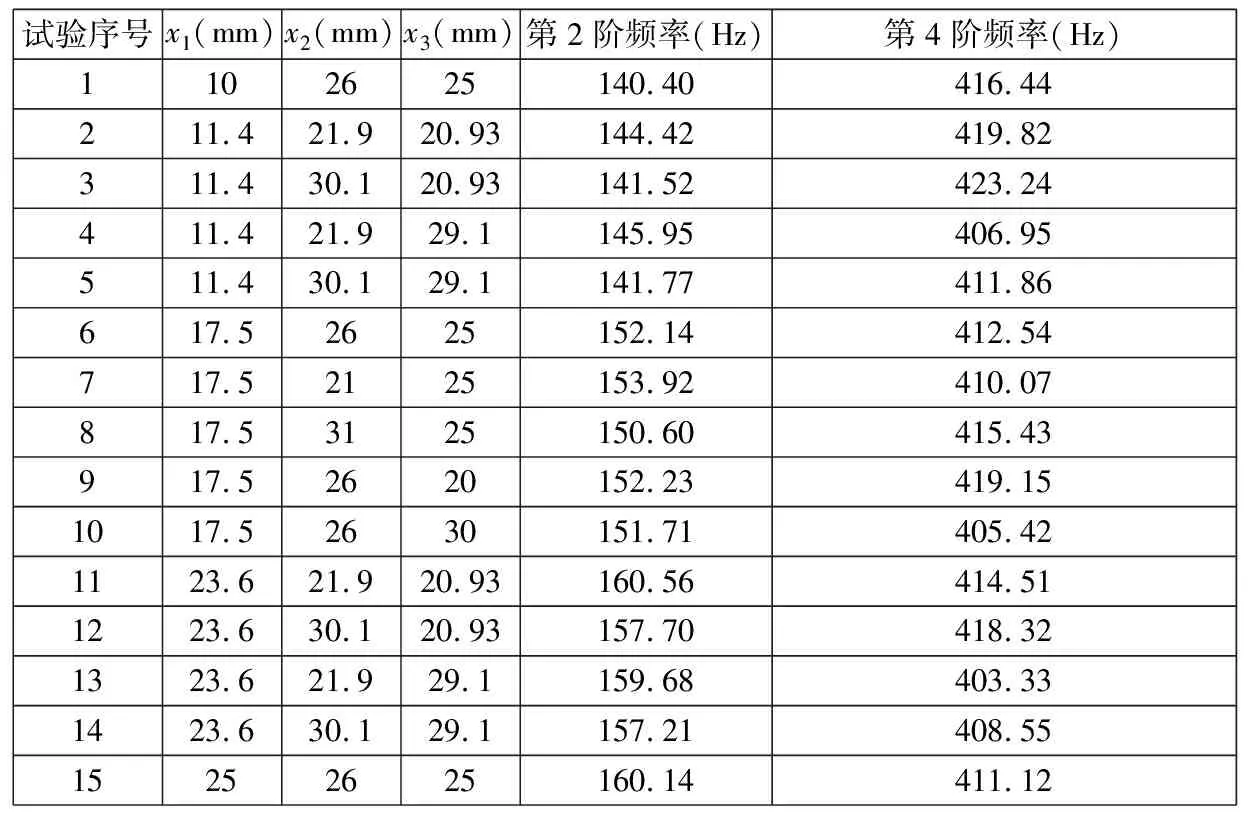
表4 基于中心复合设计的有限元试验结果
根据表4试验结果,以各设计变量对2阶固有频率、4阶固有频率的影响为例,利用二次插值函数构造设计空间的3D响应面,如图2所示。
3 机壳结构优化结果分析
基于DOE试验优化所得的有限元计算结果拟合出的响应面模型,计算得出了3组优化解,如表5所示。
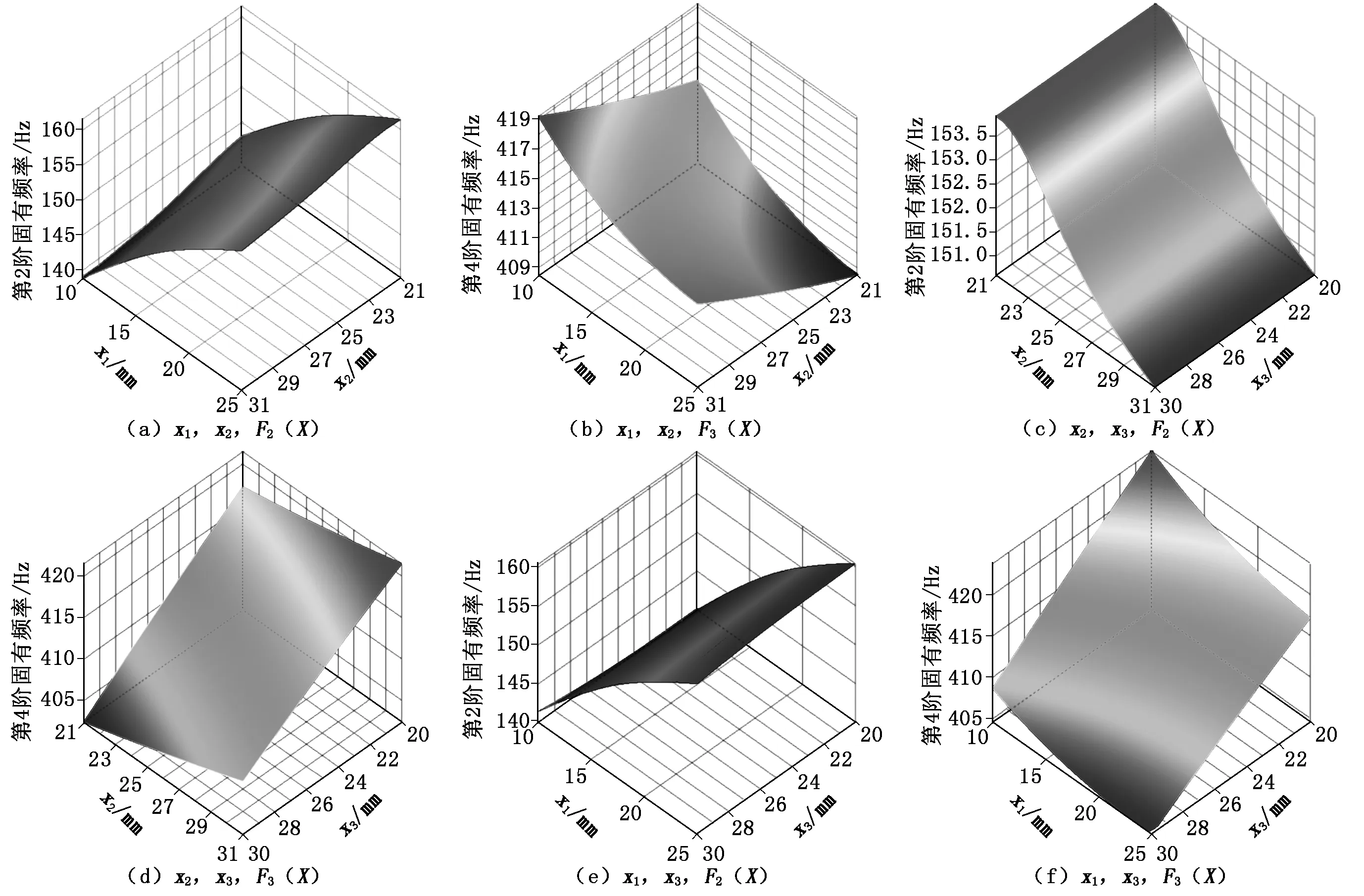
图2 各设计变量对第2阶、4阶固有频率的响应面
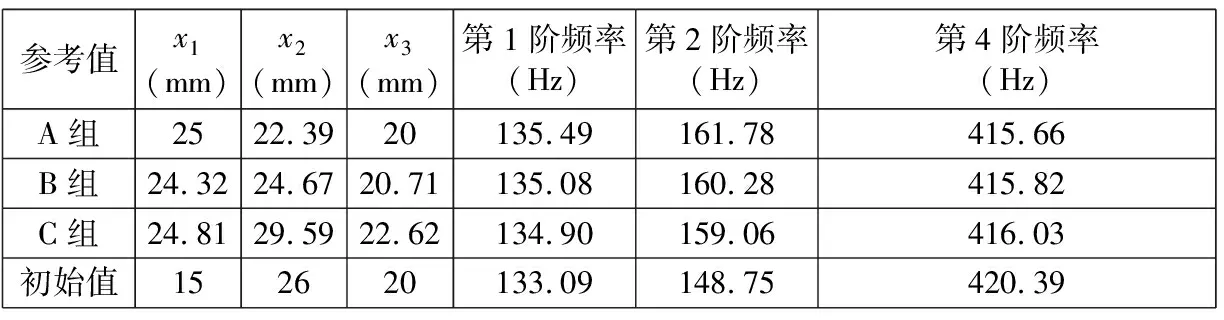
参考值x1(mm)x2(mm)x3(mm)第1阶频率(Hz)第2阶频率(Hz)第4阶频率(Hz)A组2522.3920135.49161.78415.66B组24.3224.6720.71135.08160.28415.82C组24.8129.5922.62134.90159.06416.03初始值152620133.09148.75420.39
从表5可知:A组参考值的2阶频率最优,但1阶频率相对其他两组偏高;C组参考值1阶频率升高最小,但第2、第4阶频率结果未有A组参考值优秀;B组参考值介于A、C两组之间。结合实际工况,在机壳结构尺寸不发生太大改变的情况下A组优化结果最为合适,修改结构后的第2阶固有频率为161.78 Hz,偏离1 450转速下1倍脉动频率值(145 Hz)16.78 Hz;第4阶固有频率为415.66 Hz,相比2 100转速下2倍脉动频率(420 Hz)偏离4.34 Hz。修改结构后可以有效地避开现有工况下的激振频率,减小耦合共振。
4 结语
通过风机壳体模态分析结果及气体压力脉动分析结果发现了风机在运行中原机壳体的第2阶、第4阶固有频率易与叶轮转子产生的气体压力脉动频率产生流固耦合振动。选取较为可行的结构几何尺寸作为设计变量,利用DOE中心复合设计原理,合理布置试验点位置,从而利用少量试验点拟合出精度较高的响应面,再根据拟合出的响应面模型,对机壳进行参数优化设计,针对机壳第2阶和第4阶固有频率进行了结构动力修改,使得改进后的机壳固有频率分布更为合理,改进后的机壳固有频率偏离现有工况下的气体脉动频率,改善了机壳的动态性能。

