基于梯度化因子功能梯度点阵夹层结构优化设计

朱凌雪， 王同银， 朱晓磊

(1. 金陵科技学院 数学系, 南京 211169； 2. 南京工业大学 机械与动力工程学院， 南京 211816)

金属点阵材料是一种先进的轻质多功能材料，点阵结构具有高孔隙率和较高的可设计性，使其在保证结构刚度和强度的同时，能满足多种性能要求，如抗冲击、吸能等特性[1-2]。国内外学者对点阵结构的力学性能做了广泛的研究。韩宾等[3]首次比较了波纹夹芯板、方孔蜂窝夹芯板、三角蜂窝夹芯板、金字塔夹芯板四种典型点阵金属夹芯板在受刚性物块低速冲击时的动态行为，以考察点阵金属夹芯结构的动态响应及抗冲击性能。郭锐等[4]对填充陶瓷棒的金属点阵夹层结构抗弹丸侵彻能力进行了试验研究。Dharmasena等[5-6]结合实验和数值模拟研究了金字塔夹芯板、波纹夹芯板以及等质量实体板在空爆载荷下的动态响应。Zhang等[7-10]对六边形蜂窝、不连续十字型点阵夹层结构、折纹管的抗爆吸能特性进行了研究。

现有的研究表明，梯度结构比非梯度结构具有更优的吸能效果。王晓凯[11]通过数值模拟研究了梯度蜂窝的动态力学行为，发现在初始冲击速度不是很高的情况下，梯度蜂窝相比于质量相等的均匀蜂窝具有优异的吸能特性。亓昌等[12]研究发现梯度铝泡沫夹芯板的总吸能量和同质量的均匀铝泡沫夹芯板相比，前者有较大幅度的提高。

本课题组针对功能梯度点阵夹层结构平压力学性能和空爆载荷作用下的吸能特性进行了系统的研究，建立了功能梯度点阵夹层结构空爆载荷作用下的有限元计算方法。在此基础上，本文提出采用梯度化因子表征功能梯度点阵夹层结构的梯度化程度，结合ANSYS/LS-DYNA有限元软件讨论了梯度化因子对结构抗爆吸能的影响，并基于梯度化因子采用遗传算法对梯度结构进行优化。

1 有限元模型

功能梯度点阵夹层结构，如图1所示。点阵芯子采用金字塔型胞元，芯杆截面示意图，如图2所示。其中H1，H2，H3依次为迎爆面板、芯层、背板的厚度，W1，W2分别为芯杆上下水平截面边长，θ为芯杆与背板之间的夹角。计算模型示意图，如图3所示。采用球形装药，14×14胞元的功能梯度点阵夹层结构。由于结构在爆炸载荷作用下的响应属于高度非线性问题，求解时间长。且考虑到研究对象的对称性，所以夹层板取完整模型的1/4。

图3 爆炸模型示意图

材料模型选用与应变率相关的随动塑性模型，用关键字*MAT_PLASTIC_KINEMATIC定义，点阵芯子及面板均采用AISI 304不锈钢，具体参数见表1。

表1 材料参数[13]

为反映点阵夹层结构各部分之间的相互作用，面板与芯子的界面接触通过关键字*CONTACT_TIED_SURFACE_TO_SURFACE来定义。面板与芯子的非界面区域通过*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE定义接触。点阵芯子在冲击变形过程中可能存在自身单元的相互接触碰撞，故添加点阵芯子的自接触关键字*CONTACT_AUTOMATIC_SINGLE_SURFACE。

爆炸载荷采用CONWEP算法模拟，由LOAD_BLAST模型施加在迎爆面板上，TNT当量为300 g，炸点距离为200 mm，设置求解结束时间为4 000 μs。

为了验证本文所采用的有限元建模方法，根据文献[5]，建立了材料为AL6XN不锈钢的四棱锥点阵夹层结构的有限元模型，模型尺寸以及材料参数均参照于文献中的数据。在数值计算中，爆炸载荷施加在迎爆面板上，TNT当量为201 g，炸点高度150 mm，仿真时间4 000 μs。计算结果，如表2所示。从表2可知，模拟值与文献模拟值吻合较好，最大误差为3%。

表2 面板最大变形对比结果

为了检验数值模拟的准确性，排除模型网格对计算结果的影响，对点阵夹层板进行网格独立性检验，如表3所示。

表3 不同网格大小下的结果对比

对比上述四种情况，分析结果可知，由网格引起的结果差异很小，ASEA误差最大不超过3.3%，Max D误差最大<1.3%。考虑到计算耗费的时间，在本文的计算中，均是按第一种情况的总体网格尺寸划分网格，即采用总体控制方法控制网格密度，面板最大网格边长为1 mm，芯子最大网格边长为0.5 mm。

点阵芯子及面板各部分均用六面体网格划分，以提高计算精度，单元类型为SOLID164。数值模型中，模型对称面施加对称约束。夹层结构采用四周固支的方式，故对端面施加全约束。

2 梯度化因子对结构抗爆性能的影响

2.1 梯度化因子定义

文献[11]中指出密度梯度参数可描述为

(1)

式中：γ为无量纲参数，ρ0为样本的平均密度，L为样本在x方向上的长度。沿x轴正方向密度逐渐增加的称为正梯度(γ>0)材料，密度逐渐减小的称为负梯度(γ<0)材料。

在本文中定义如下

(2)

式中：γ1为面板的梯度化因子；γ2为芯子的梯度化因子。当γ<1时，结构为正向梯度化；当γ>1时，结构为逆向梯度化。

本文是在夹层结构相对密度相同的前提下，做梯度化因子的相关探讨，故结构参数定义如下约束条件：H1+H3=4 mm，W1+W2=4 mm，H2=24 mm，θ=50°。

为探讨面板梯度化因子、芯层梯度化因子分别对功能梯度点阵夹层结构抗爆吸能的影响，引用结构的面比吸能(Areal Specific Energy Absorption, ASEA)作为评价指标[12]，共建立11组模型，并利用ANSYS/LS-DYNA完成仿真计算。

面比吸能表达式为

(3)

式中：MA表示结构单位面积内的质量，En表征结构的总吸能。

2.2 面板梯度化因子γ1的影响

对于本文的研究对象而言，t=800 μs时，夹层结构背板变形量达到最大，所以取该时刻进行状态分析，对比更明显。图4为t=800 μs时不同面板梯度化因子γ1对应的夹层板变形响应图，图5为该时刻γ1=1/3的夹层结构对应的迎爆面板局部凸起示意图。由图4可知，γ1不同时芯层表现出的变形模式有差异；当γ1=1/3、3/5时，迎爆面板不仅会发生整体弯曲，还会在点阵芯子与面板连接的位置出现局部的凸起；且γ1=1/3的凸起高度要大于γ1=3/5，说明面板壁厚减薄导致面板抵抗塑性变形能力降低，面板的塑性变形成为主要的吸能方式。面板梯度化因子对功能梯度点阵夹层结构抗爆吸能的影响，如图6所示。不同γ1时各部件吸能情况如图7所示。从图6可知，随着γ1的增加，结构的面比吸能减小。这是由于γ1增大时，迎爆面板的厚度相应增加，抗弯刚度增大，结构抵抗变形的能力增大，结构不易发生塑性变形；同时，面板厚度增加承载面积增加，在相同载荷条件下，迎爆面板局部剪切应力和拉伸应力减小，不易达到塑性屈服应力，使得吸能减小。由图7可知，当γ1<1时，上面板和点阵芯子的吸能特性被明显加强，这是因为，面板减薄后，面板的局部塑性变形加剧导致面板吸能增加，而面板局部塑性变形增加的同时，使得芯子除了承受轴向载荷以外，还要受到由面板局部变形引起的横向载荷，使得芯子塑性铰增多导致芯子吸能增加。当γ1>1时，面板吸能趋于稳定，点阵芯子的吸能逐渐减小，说明随着迎爆面板厚度的增加，迎爆面抵抗塑性变形的能力增加，冲击动能大部分转化为弹性势能被结构储存，结构吸能主要依赖于面板的刚度，因此，上面板吸能区域稳定；随着上面板厚度的增加，点阵芯子仅受到轴向载荷的作用，且轴向载荷逐渐减小，使得点阵芯子发生塑性变形的能力减小，导致芯子吸能降低。

γ1=1/3γ1=5/3

γ1=3/5γ1=7/3

γ1=1γ1=3

图4t=800 μs时夹层板的变形响应图(γ2=1)

Fig.4 Deformation response of sandwich panel at the time of 800 μs (γ2=1)

图5 t=800 μs时迎爆面板局部凸起示意图(γ1=1/3)

图6 ASEA随γ1变化关系(γ2=1)

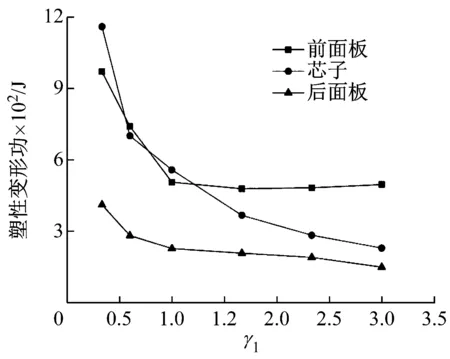
图7 不同γ1时各部件吸能

2.3 芯层梯度化因子γ2的影响

图8为t=800 μs时不同面板梯度化因子γ2对应的夹层板变形响应图。由图8可知，γ2不同时芯层表现出的变形模式差异很大。当γ2=1/3时，塑性铰出现在靠近迎爆面板侧且为杆长1/3的位置，且芯杆小端发生了明显的扭曲；当γ2=3/5时，塑性铰出现在杆长1/3和2/3的位置；当γ2=1时，塑性铰出现在杆长1/2的位置；当γ2>1时，除去杆件两端不考虑，沿杆件方向均只有一个塑性铰，且随着γ2的增大，塑性铰的位置也逐渐靠近背板。

芯层梯度化因子对功能梯度点阵夹层结构抗爆吸能的影响，如图9所示。从图9可知，随着γ2的增加，结构的面比吸能整体有缓慢减小的趋势。这是因为随着γ2增大，在承受爆炸载荷时，芯杆上端越不容易发生塑性弯曲，会使得结构吸能有所降低，但由于芯子变形受到面板约束较大，在面板厚度一定的时，芯子发生塑性变形的能力有限，故改变γ2时吸能变化幅度很小。对比图6、图9可知，正向梯度化可以提高结构吸能，且γ2对面比吸能的影响程度远不及γ1。

γ2=1/3γ2=5/3

γ2=3/5γ2=7/3

γ2=1γ2=3

图8t=800 μs时夹层板的变形响应图(γ1=1)

Fig.8 Deformation response of sandwich panel at the time of 800 μs (γ1=1)

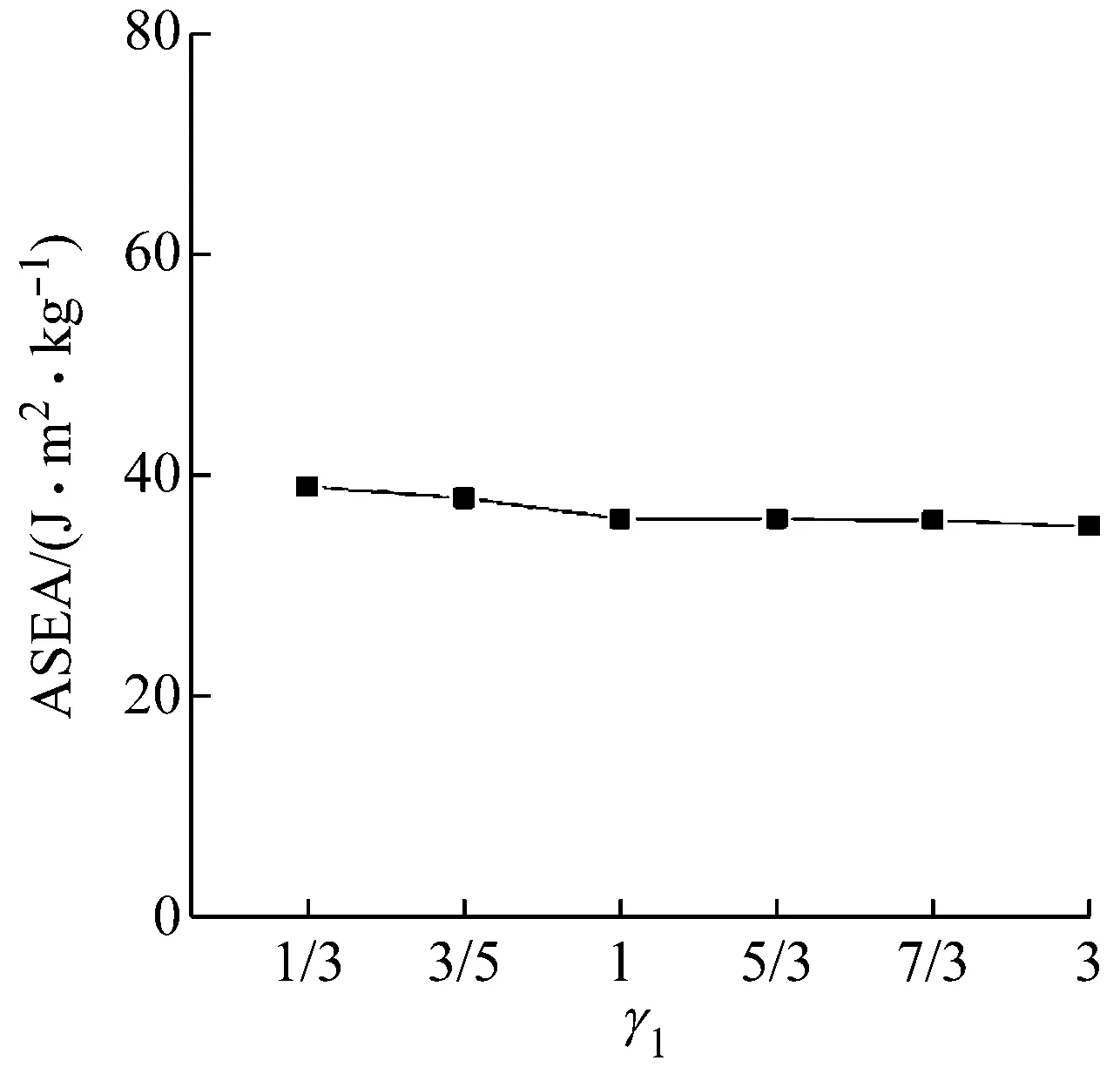
图9 ASEA随γ2变化关系(γ1=1)

3 功能梯度点阵夹层结构优化设计

3.1 响应面模型的构建

本文旨在基于梯度化因子对功能梯度点阵夹层板进行结构优化设计，故以面板梯度化因子γ1、芯子梯度化因子γ2作为设计变量；为考察梯度结构的吸能特性，以结构的面比吸能ASEA为优化目标；考虑结构达到最大吸能时，面板或芯子不能发生破坏，故以面板的有效应变作为状态变量。在满足设计变量、约束条件的基础上，求ASEA最大值。

优化目标：max(ASEA)

对γ1和γ2两个因素，均取六个水平γ1,2=1/3、3/5、1、5/3、7/3、3。考虑到因素数量少，且为获得真实可靠的结论，所以采用全因子试验设计，建立如下36组模型，见表4。

表4 试验设计及仿真结果

构建响应面模型主要有两种思路：① 利用神经网络建立映射关系；② 采用回归分析方法得到回归方程。由于通过神经网络得到的响应面模型不能用数学表达式直观表征出来，且神经网络的计算精度与构件模型的隐含层数和神经元的数目有关，使得神经网络的构建的模型好坏具有一定的随机性，所以在本文中采用回归分析的方法建立响应面模型。利用四阶多项式对仿真数据点进行曲面拟合，得到如下拟合公式：

(4)

响应面模型的精度直接关系着后续结构优化的准确性，而响应面模型的精度主要与模型中方程拟合的参数有直接的关系。本文所拟合的响应面模型，其平方和误差为SSE=24.88，均方根误差为RMSE=1.088 5，R2为0.997 4，说明拟合模型与实际计算结果吻合较好，误差<5%。

拟合曲面，如图10所示。并依据拟合方程进行残差分析，定义残差e=ASEA仿真-ASEA拟合。

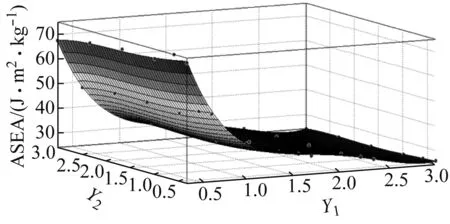
图10 ASEA曲面拟合图

判断回归模型合适程度最有效方法之一是对因变量与残差作图，观察其分布情况，如图11所示。由图11可知，残差所在位置互不关联，是随机的，残差值的分布基本符合正态分布，因而回归模型是可靠的。

(a)

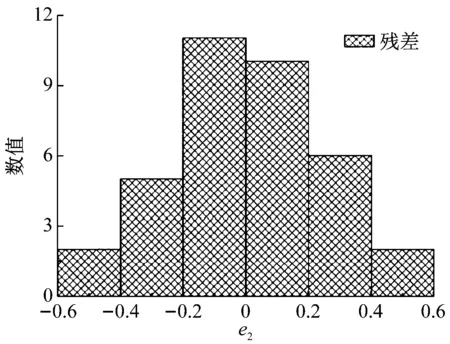
(b)

3.2 优化求解

遗传算法是一种建立在自然选择原理和自然遗传机制上的迭代式自适应概率性寻优算法，模拟生物进化过程达到寻优的目的[14]。它的程序简单，计算过程仅涉及目标函数和约束条件的分析比较，能够很好地获得全局最优解。且在结构中主要应用于桁架的结构、形状和拓扑优化、复合材料铺层优化、布局优化、多目标优化等方面[15]。基本遗传算法的流程，如图12所示。

图12 基本遗传算法流程框图

本文中以拟合方程式(4)作为目标函数，运用遗传算法进行优化求解。设置迭代次数1 000，种群规模50，交叉概率0.4，变异概率0.2。图13表示面比吸能的优化迭代过程。得到当γ1=γ2=1/3时，拟合方程式(4)有最大值73.6。

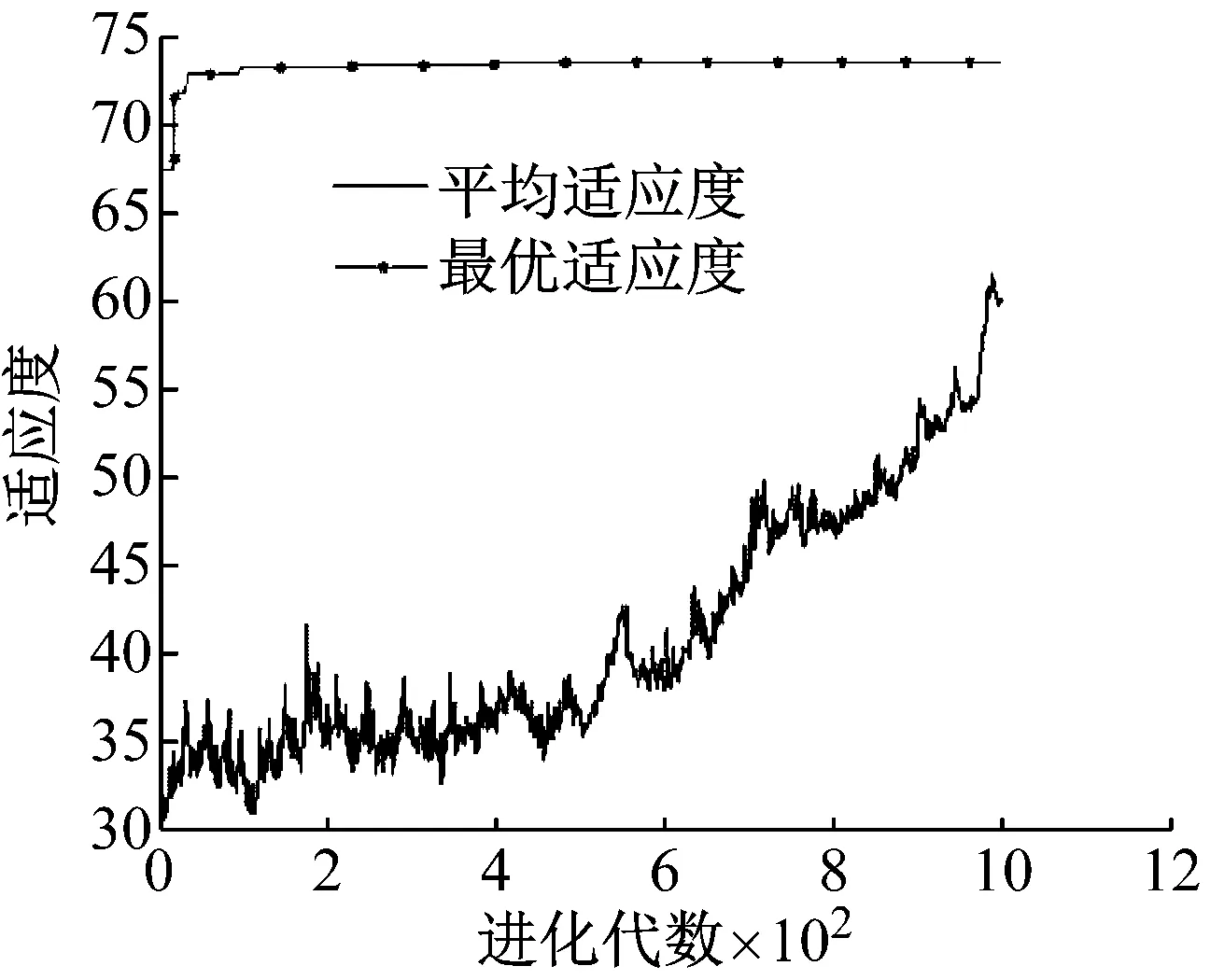
图13 优化过程监控：适应度-面比吸能

由优化结果可知，如表5所示。面板和芯层均采用正向梯度化能提高结构吸能，且面板梯度化因子γ1、芯层梯度化因子γ2均为1/3时，夹层结构的面比吸能最大。因为此时迎爆面板不仅有整体变形还有大范围的局部凹凸变形；芯杆整体失稳且芯杆小端扭曲严重，发生明显的塑性变形。

表5 优化结果

将优化结果与常规点阵(即非梯度点阵)对比，发现在相同结构条件下，优化结果的ASEA为73.6 J·m2/kg，而有限元计算结果为74.8 J·m2/kg，这是因为响应面是通过曲面拟合的方式得到的，与实际值有一定偏差，本文预测的最优结果与计算值的误差<2%，说明本文所拟合的响应面模型及优化结果是正确的。从表5可知，优化结构与常规点阵相比，吸能值提高了一倍，可见梯度结构有极大地吸能优势。

4 结 论

本文提出了梯度化因子的概念，采用有限元仿真的方法探讨了梯度化因子对功能梯度点阵夹层结构抗爆吸能的影响，并运用遗传算法对梯度结构进行结构优化，可得到以下结论：

(1) 梯度化因子的改变会影响点阵夹层结构的变形模式。随着梯度化因子的增加，结构的面比吸能减小，但面板梯度化因子γ1与芯层梯度化因子γ2相比，前者对结构吸能特性的影响更为显著。

(2) 当γ1<1且γ2<1时，结构的吸能优于其他情况，说明同时考虑面板和芯子的正向梯度化能更好地提高结构吸能。

(3) 当γ1=1/3且γ2=1/3时，梯度结构与常规点阵相比，吸能值提高了一倍，说明梯度点阵具有极大的吸能优势。