考虑摩擦非线性应力的脐带缆疲劳寿命精确分析研究

卢青针， 杨志勋， 陈金龙， 熊飞宇， 阎 军， 岳前进,

(1. 大连理工大学 海洋科学与技术学院，辽宁 盘锦 124221；2. 大连理工大学 运载工程与力学学部工程力学系，辽宁 大连 116024；3. 大连理工大学 盘锦产业技术研究院，辽宁 盘锦 124221)

钢管脐带缆是深水水下生产系统开发模式中的关键装备之一，主要由电缆、光缆、钢管、填充、铠装钢丝及护套组成，为水下生产系统提供电能、传输数据信号以及液压和化学药剂注入。脐带缆采用非粘接螺旋缠绕结构形式，各单元间可滑动，具有良好的弯曲性能。动态脐带缆连接海上浮式控制平台和水下生产设备，在浮体运动，波浪荷载及自身重量作用下，与浮体连接的顶部受到较大的拉伸荷载与反复弯曲荷载的组合作用。其荷载往复周期往往较长，为典型的低周振动疲劳荷载。在服役期间，长期的动态响应将导致脐带缆内部单元交变应力的累积，进而产生损伤引起疲劳破坏。

基于Miner累计算上准则的疲劳寿命分析方法由于其应用方便，并具有一定可靠性而被海洋工程相关规范推荐使用。但由于脐带缆自身结构的复杂性，动态脐带缆的疲劳寿命预测在分析方法上还存在许多不确定的因素。Hoffman等[1-2]均基于Miner疲劳累积损伤方法提出了动态脐带缆与柔性立管的疲劳寿命分析流程。宋磊建等[3-4]对不同线型的脐带缆给出了张力和曲率动态响应特性，并研究了浮子结构参数对整体响应敏感性。李清泉等[5]考虑脐带缆整体动态响应给出了其与平台在波浪流荷载下的干涉特性。目前，针对脐带缆疲劳寿命分析的研究中，柔性立管/缆整体荷载的动力分析计算方法已经相对比较成熟。然而对于局部应力的分析还不完善，在刚性立管疲劳分析中，金属管道上的局部交变应力可以通过简单公式直接计算出来，但对于脐带缆这种复合结构，尤其是考虑单元间相互接触摩擦引起的非线性因素，使得局部应力分析比较困难。Skeie等[6]将拉伸荷载引起的应力，弯曲荷载引起的应力以及摩擦引起的应力进行理论分析，叠加得到局部应力用于疲劳寿命预测模型。Knapp等[7]建立了脐带缆结构的二维有限元模型进行截面变形和应力分析，将螺旋铠装钢丝、聚合物护套等所有单元采用环形宏单元进行模拟。Svik[8-9]采用曲梁单元来模拟，同时使用弹簧单元设置各个单元之间的非线性接触摩擦。Wang等[10]对不考虑摩擦与考虑摩擦的脐带缆疲劳进行数值分析，结果表明考虑摩擦与否使疲劳寿命结果相差将近10倍。Parsinejad等[11]考虑单元摩擦和内部压力等非线性因素，对两种不同类型的钢管脐带缆进行疲劳应力和寿命分析。Probye等[12]使用ABAQUS软件对钢管脐带缆结构响应进行分析，单元之间采用接触模拟其相互作用，并可以设置库伦摩擦。随后，Le Corre等[13]为节约计算资源并保证计算精度改进了这个有限元模型，全部单元都采用了梁单元，单元之间的相互作用全部变为线-线接触。李清泉等[14]建立了包含六个钢管的脐带缆三维有限元模型，分析不同工况下的应力以及摩擦因数对应力的影响。

本文考虑平均应力的影响基于Miner损伤累积准则构建了脐带缆疲劳寿命分析方法，在局部应力计算时考虑钢管脐带缆单元间相互摩擦作用引起的非线性应力，采用Orcaflex软件建立数值分析模型进行疲劳寿命预估。对中国南海某1 500 m水深的动态脐带缆算例进行分析，结果表明：考虑无滑动假设的局部应力作为输入，得到的疲劳寿命过分偏于保守；而采用全滑动假设计算的局部应力作为输入，得到的疲劳寿命则偏大很多。在疲劳寿命预估模型中考虑非线性局部应力作为输入可以得到更为准确的寿命估计，为脐带缆设计分析及工程应用提供强有力的技术支撑。

1 疲劳寿命分析方法

基于材料S-N曲线的Miner损伤累积方法计算疲劳寿命，首先计算短期海况下的整体荷载响应时程，随后计算荷载分配到单元的局部应力并组合成局部应力时程，最后结合危险单元材料的S-N 曲线，依据概率统计出长期的疲劳累积损伤，从而获得疲劳寿命。在DNV及API[15-16]规范均推荐使用此方法对海洋结构物进行疲劳计算，并且在动态脐带缆疲劳寿命计算中推荐采用10倍安全系数[17]。

基于Miner累积损伤理论的动态脐带缆疲劳寿命分析方法，主要的步骤如下：

步骤1整体响应分析。整体响应分析采取时域分析方法，用集中质量法求解方程。将脐带缆划分成为一系列没有质量的线段和相应节点，每个线段模拟脐带缆的轴向、扭转及弯曲刚度性能，质量、重力及浮力等特性则全部集中到相应节点上[18]。基于Longuet-Higgins方程[19]，将给定的不规则波浪散布图离散为一系列的具有代表性的规则波的波浪散布图。分别计算每个海况下的拉伸和曲率荷载时程。每个海况一年之内发生次数的概率百分比为pi，对应这种工况的周期记为Tzi，一年之中此种工况实际发生的次数ni，计算公式为

ni=365×24×3 600×pi/Tzi

(1)

步骤2局部应力分析。将整体分析得到的拉力及曲率荷载作用在局部结构上，用于计算脐带缆中易发生疲劳失效的单元的局部应力。局部应力的计算基于以下方程

σ=KtT+Kc(Cxsinθ-Cycosθ)

(2)

式中：Kt为有效张力—应力系数；Kc为曲率—应力系数；θ为计算点处应力沿圆周分布的位置；Cx为缆单元x方向的曲率分量；Cy为缆单元y方向的曲率分量。

步骤3材料S-N曲线。单元的抗疲劳能力一般由材料的S-N曲线表示。S-N曲线表示在交变应力Δσi下，单元经过Ni次发生疲劳破坏。

Ni=10a(Δσi)-m

(3)

Lg(Ni)=a-mLg(Δσi)

(4)

式中：Ni为交变应力循环的破坏次数；a和m均为实验得到的材料常数。

面前脐带缆疲劳寿命估算中通常不考虑平均应力对构件疲劳寿命预测的影响，而平均应力对疲劳寿命的影响程度仅次于交变应力幅值对其的影响。通常疲劳设计参考材料 S-N 曲线，其数据是将标准试件在对称循环应力即应力比为-1 作用下进行疲劳测试采集得到，对应的疲劳极限应力为σ-1。而脐带缆在实际运行过程中，由于自重和浮体运动，管体顶部承受较大的拉伸荷载，导致缆体内部结构受到非对称循环应力作用，即平均应力不等于 0。研究发现平均载荷虽然不是造成疲劳的主要原因，但是对疲劳寿命有一定的影响，且不能忽略[20]。为了消除平均应力对疲劳寿命的消极作用，许多学者提出了不同的修正方法，其中的古德曼线由于简单、应用方便，因此多数工程的抗疲劳设计采用古德曼线对疲劳极限曲线进行简化并修正平均应力。

图1 中的直线AB代表古德曼线，横轴表示平均应力，纵轴为应力幅值。每一个点表示经过某一指定循环次数下，发生疲劳失效的循环应力，其中A点的横坐标平均应力为 0，表示其疲劳应力为σ-1；B点的坐标为(σb，0)，其中σb是强度极限；任一点C的横坐标平均应力不是 0，即交变应力是非对称的循环应力，不能直接根据标准S-N曲线查找得到此应力水平对应的循环次数N。而古德曼线上的所有的点具有相同的疲劳循环次数，同时根据式(5)可以将C点在非对称循环应力作用下疲劳分析问题转化为A点平均应力为零的对称循环疲劳寿命分析研究。

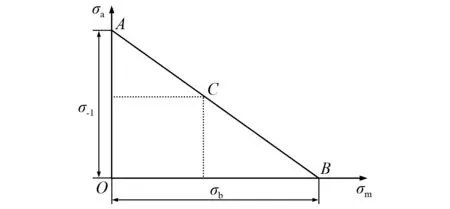
图1 古德曼线Fig.1 Goodman line

(5)

式中：σa为C点的应力幅值；σ-1为应力循环比r=-1时疲劳极限；σm是为C点的平均应力；σb是强度极限。

步骤4脐带缆的疲劳寿命。根据上述公式计算的结果，利用Miner公式，可以得到一年之中的疲劳损伤累积，如式(6)所示

(6)

式中：N为交变应力种类的个数；D为疲劳损伤累积量。当D=1时，说明疲劳发生破坏；当D=0时没有发生疲劳损伤。脐带缆的疲劳寿命为疲劳损伤的倒数，即

(7)

2 局部应力分析

典型钢管脐带缆结构如图2所示，截面中大部分单元以一定螺旋角度铺设。其中内部单元的缠绕角度一般小于10°。钢管脐带缆最易发生疲劳破坏、破坏后功能失效最为严重的往往是钢管单元，故需要对钢管单元在拉伸和弯曲荷载作用下的应力做分析计算。造成钢管单元疲劳的主要因素有拉伸、弯曲和摩擦引起的应力。由于钢管缠绕角度较小，故在拉伸及弯曲引起的应力分析中忽略钢管角度影响。

图2 钢管脐带缆结构组成Fig.2 Compositions of a steel tube umbilical

2.1 拉伸引起的应力

拉伸荷载分配到每个钢管单元上的应力由总的拉伸刚度及钢管单元的拉伸刚度决定。拉伸引起的应力通过式(8)计算。

(8)

式中：ΔσT(t)为拉伸应力时间历程；T(t)为整体拉伸荷载的时间历程；KT为脐带缆的拉伸刚度；E，A分别为钢管的弹性模量以及面积。

2.2 弯曲引起的应力

脐带缆弯曲时内部单元会将经历从无滑动阶段到滑动阶段，并且拉力荷载将会加大无滑动阶段的长度，因此弯曲应力可分段表示。

2.2.1 无滑动弯曲应力

滑动之前，钢管以脐带缆的中心轴为轴进行弯曲，弯曲应力即为静摩擦应力可采用如式(9)表示

ΔσFB(t)=κ(t)EFL

(9)

式中：ΔσFB(t)为无滑动的弯曲应力时间历程；κ(t)为整体曲率荷载的时间历程。RL为钢管中心到脐带缆中心距离。

滑动后，弯曲荷载分配到每个钢管的应力由钢管的直径决定。弯曲引起的应力可以通过以下公式计算。

ΔσBC(t)=κ(t)ER

(10)

式中：ΔσBC(t)为滑动后弯曲应力时程；R为钢管的半径。

2.2.3 滑动摩擦应力

钢管单元发生全滑动时，静摩擦力转化为动摩擦力。假定滑动只发生在沿螺旋轴向方向，忽略端部效应。对其中一个螺旋钢管单元进行分析，如图3所示。基于弯曲引起的轴向力与阻止轴向位移的静摩擦力的平衡关系可以建立摩擦应力分析模型。

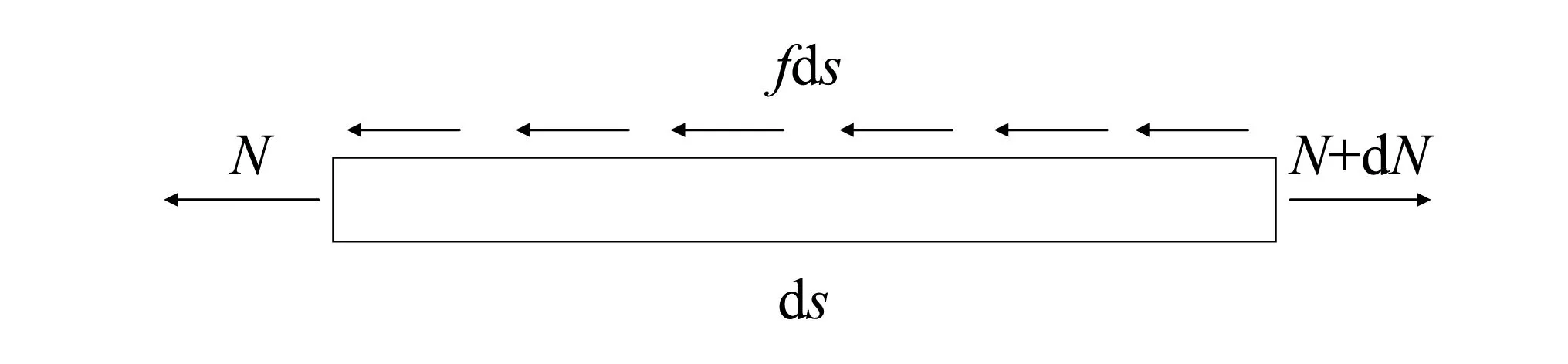
图3 微螺旋单元ds的受力图Fig.3 Force on infinitesimal helix element ds

基于钢管单元的轴向方向平衡条件，给出如下的滑动准则

（2）有利于简化物流园区项目中的合同关系。在EPC总包模式下，业主不需要再与设计方、采购方和实施方分别签署合同，只需与总包方达成一致，极大地简化了智慧物流园区项目的合同框架。

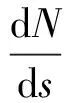
(11)

式中：N为轴向力；f为单位长度的摩擦力。

假定螺旋钢管单元完全固定在所缠绕的圆柱上，由弯曲引起的轴向力的可表示为

N=-EARLcos2αsin(φ)κ

(12)

式中：α为钢管的缠绕角度；φ为螺旋位置的角度；φ与沿螺旋方向的长度S的关系可表示为

(13)

静摩擦力阻止单元滑动，当单元轴向力梯度(dN/dS)达到单位长度的静摩擦力f时滑动发生。可表示为

(14)

当φ=0时，拉力梯度有最大值，在中性轴处开始滑动，因此可得到开始发生滑动的临界曲率

(15)

单元从中性轴位置最开始发生滑动到全滑动时，总的摩擦力F达到静摩擦力值N。

(16)

(17)

(18)

此时可得到滑动的摩擦应力σFC为

(19)

单元摩擦力跟摩擦因数及接触压力、接触长度有关。

f=μqcLc

(20)

准确确定钢管与相邻单元的摩擦因数μ、接触应力qc及长度Lc是计算摩擦力的关键，本文基于ANSYS二次开发APDL语言建立参数化有限元模型进行接触压力分析。将拉伸引起的径向接触压力作用在缆芯结构上计算截面内危险管单元的接触应力qc及接触长度Lc，进而计算滑动摩擦应力。脐带缆缆芯二维有限元模型如图4所示。

图4 脐带缆二维有限元模型Fig.4 2D model of the umbilical core

2.3 局部应力

无滑动时，钢管单元的局部应力组合Δσ(t)为拉伸应力、弯曲应力的和。

Δσ(t)=ΔσT(t)+ΔσFB(t)

(21)

滑动时，钢管单元的局部应力组合Δσ(t)为拉伸应力、滑动弯曲应力及滑动摩擦应力的和。

Δσ(t)=ΔσT(t)+ΔσBC(t)+ΔσFC(t)

(22)

3 数值算例

3.1 算例介绍

某1 500 m水深的动态脐带缆采用如图5所示悬链线形式线型。海床平坦，土壤可以作为沙质粉土考虑，脐带缆采用图1中的结构形式。表1、表2分别给出了脐带缆系统参数及结构参数。脐带缆系统的基本参数包括脐带缆的长度及SPAR平台的参数；脐带缆结构参数包括外径、质量、拉伸刚度及扭转刚度参数。通过实验室原型弯曲实验对该脐带缆进行弯曲刚度实验，测得的非线性弯矩-曲率关系，如图6所示。

图5 1 500 m水深动态脐带缆Fig.5 A dynamic umbilical in depth of 1 500 m

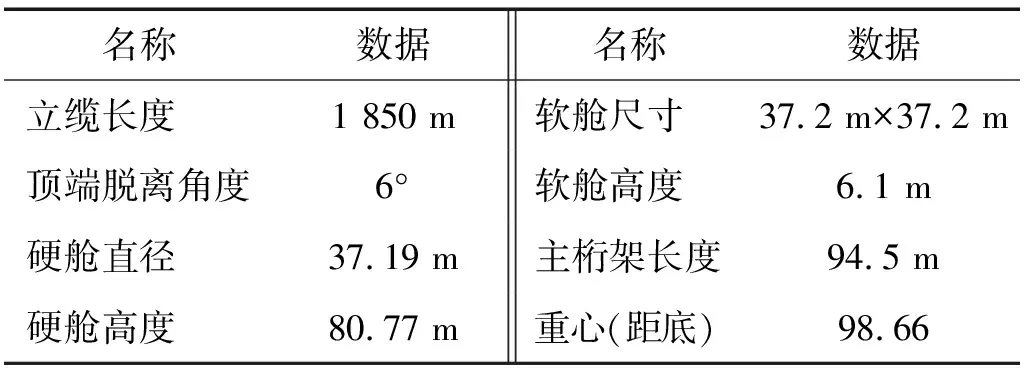
表1 脐带缆系统主要参数Tab.1 Parameters of umbilical system

表2 脐带缆结构参数Tab.2 Parameters of the umbilical cable

本文基于Longuet-Higgins方程，将给定的不规则波联合概率分布，离散为规则波的波浪散布图，覆盖率达99%。本文计算所采用的规则波工况如表3所示。分析时考虑了浮体位于远位、近位、侧位时的情形，设各占33.33%概率。其中波浪迎浪0度占60%，迎浪角为30度时占40%。波浪联合概率分布，转化为规则波散布图块为42块，共有252种荷载工况。

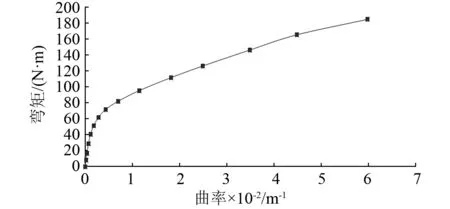
图6 脐带缆弯矩-曲率关系Fig.6 Relationship of bending moment-curvature of the umbilical

采用OrcaFlex软件建立动态脐带缆的数值分析模型，脐带缆与SPAR平台底端固接，此处吃水为164.6 m。脐带缆末端锚固于海底，脐带缆与海底轴向摩擦因数设为0.25。模型假设了1 850 m总长，即初始约为430 m的海底拖行段，浮体的运动相应数据(Response Amplitude Operator, RAO)赋于SPAR平台重心处。为了尽量真实反映脐带缆的运动，采用不同的网格划分，对其中敏感区域受力变形情况进行细化划分。将整个动态脐带缆模型分成4部分，上端与浮体连接处和触地点区域网格细化，离散成若干长度为1 m的单元，海床上静态部分及中间段离散成若干长度为5 m的单元。

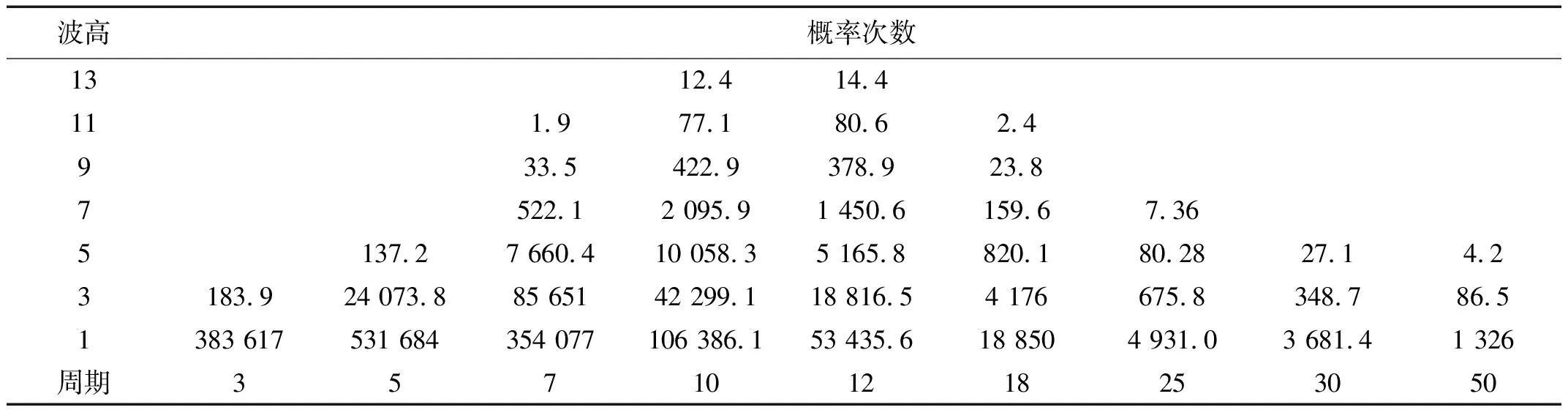
表3 脐带缆疲劳计算的规则波工况Tab.3 Regular wave case for fatigue calculation of umbilical

3.2 局部应力分析

最内层的钢管单元受到外层铠装钢丝、外层单元及相邻单元等的挤压作用，基于图4有限元模型进行接触压力分析。提取截面内单元的接触应力，其中最大的接触应力发生在外层管单元与中心管单元的接触处，提取沿圆周所有钢管单元的节点的接触压力值如图7所示。

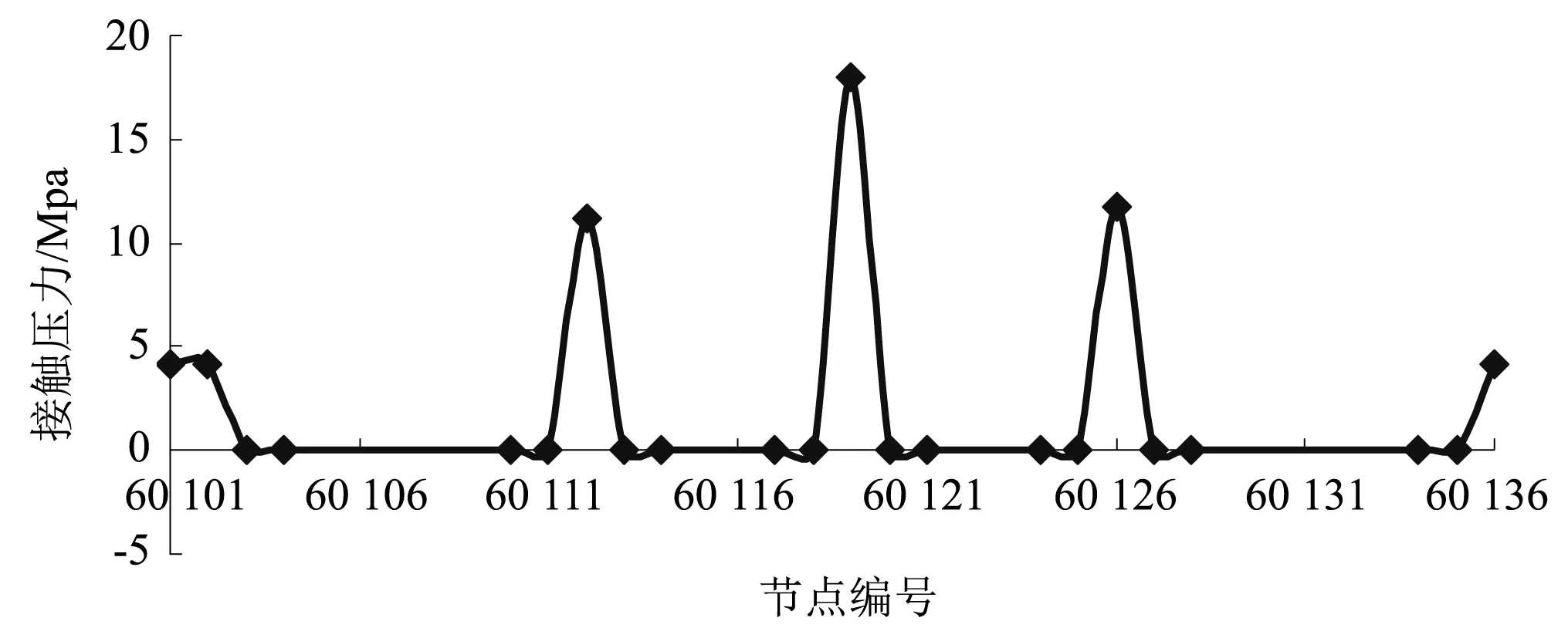
图7 沿着管单元节点的接触应力值Fig.7 Contact stress values of the nodes along the tube

根据式(18)计算滑动时的临界曲率，基于式(19)和(20)计算单位长度的滑动摩擦应力值，代入式(21)和式(22)可得钢管单元的随着曲率变化的总应力。此外考虑其他两种假设下的应力情况，一种是无滑动假设，即应力随着曲率变化一直为静摩擦应力，应力公式基于式(21)，另一种为忽略摩擦作用全滑动假设，应力公式基于式(22)。三种情况下的应力总和如图8所示。

3.3 疲劳寿命估计

计算顶部危险点的疲劳荷载工况，按无滑动假设计算的局部应力作为输入，可得脐带缆顶部危险的点疲劳寿命最低为1 850年，考虑10倍安全系数为185年。考虑非线性计算的局部应力作为输入，疲劳寿命为250年，与无滑动假设计算的相差35%。考虑全滑动假设忽略摩擦作用的局部应力作为输入，疲劳寿命为3 116年，远远大于考虑非线性局部应力时计算的疲劳寿命。

图8 总应力计算结果Fig. 8 Result of the total stress

表4 疲劳寿命分析结果比较Tab.4 Comparison of fatigue life results

4 结 论

本章针对动态脐带缆的疲劳性寿命预测进行研究。提出疲劳寿命的分析模型，在脐带缆局部应力分析中考虑单元间接触引起的摩擦。基于Orcaflex软件建立数值分析模型，采用非线性局部应力作为输入，对南海某1 500 m水深的动态脐带缆进行疲劳寿命分析，结果表明：

(1)考虑无滑动假设的局部应力得到的疲劳寿命值过于保守，相差约35%。给工程设计带来了不必要的浪费。

(2)考虑全滑动假设的局部应力得到的疲劳寿命过于偏大，导致结果偏危险。

在疲劳寿命分析中考虑非线性的局部应力作用可以得到更为准确的疲劳寿命估计。本文研究结论为动态脐带缆设计分析与工程实际应用提供有力的技术支撑。