基于结构分析的风机齿轮箱传感器配置研究

王桂兰， 赵洪山， 郭双伟

(1.华北电力大学(保定) 电气与电子工程学院，河北 保定 071003；2.国网江苏省电力公司检修分公司，南京 210029)

风电机组齿轮箱是风力发电系统中重要且故障率较高的部件之一，为了降低其维护代价、提高可靠运行时间，基于振动信号对其进行实时状态监测、故障预测与故障诊断是目前风电厂中普遍采用的方法。振动信号来源于安装在齿轮箱上的各种振动传感器，如何配置传感器，即确定传感器安装位置及个数，来获取最优信号、直接反应齿轮箱的运行状态；最有效的利用传感器，避免传感器重复浪费或缺失重要信息采集情况的发生，是风电研究领域面临的新问题。

ISO2373标准推荐，测点位置的选取要遵循测点刚度最大，传递路径最短的原则，测点的数量应能反映机器的主要运行状态。在文献[1-2]中，均采取了在所有可能安装传感器的位置均安装传感器的方法，因此在Sheng等的研究中选择了所有可能的12个位置来安装传感器，而在丁显的研究中则在齿轮箱部分安装了数量多达21个的传感器，文献[3]中仅安装了一些自身感兴趣变量的传感器。对于如何配置传感器具体的安装数量及位置，以保证实现齿轮箱相关故障诊断没有针对性的研究。

基于结构分析的传感器配置方法[4-8]，通过实验分析系统的结构及运行中各参数间的关系，推导出识别、隔离最多故障的优化传感器配置，并在很多应用中取得了良好的效果[9-12]。

风机齿轮箱内部的结构复杂，为其建立精确的振动模型模拟它的动态行为是机械力学研究者的一个严峻挑战。针对风机齿轮箱的模型进行了研究，从各分部件的角度、以不同的自由度进行了探索。文献[13]建立了考虑齿啮合和轴承间隙的行星轮模型，但其有9个自由度，在工程中实现不太容易。文献[14]中的行星轮模型包含3个自由度，且推导出系统水平、垂直方向的加速度。文献[15]建立了风机的整机模型，文献[16-17]为传动系统建立了模型，但都比较笼统，没有涉及到具体的参数。因此，本文采用了张策研究中的行星轮模型，并利用文献[16]扩展出另外两级平行齿轮模型来构成整机模型。

齿轮箱的各零件中，齿轮故障所占的比例最大，能达到60%以上。齿轮本身常见故障形式有齿疲劳、齿磨损、点蚀、断齿等类型，对齿故障的故障原因一般认为有制造误差、装配不良、润滑不良、超载、操作失误等；但这些信息在动力学模型中都无法体现。目前的研究中已证明齿故障时，啮合刚度会产生一定程度的降低[18-21]；因此，本文用啮合刚度作为发生齿故障的识别参数。

本文在前述研究的基础上，针对风机齿轮箱的物理结构进行动态建模。通过风机齿轮箱的常见故障分析，将故障信息引入到齿轮箱正常动力学模型中，获得包含故障信息的齿轮箱动态模型。在保证俘获信息精度的前提下，以传感器数量最少为目标，以包含故障信息的齿轮箱结构模型为研究对象，采用结构分析方法，获得最优的传感器配置。经过仿真验证，获得了较好的故障识别与隔离效果。

1 基于结构分析的传感器配置

1.1 结构分析理论基础

结构分析方法是一种利用系统或设备的动态模型，结合其方程组M=(e1, ...,em)与未知变量X=(x1, ...,xm)间的相关关系，进行研究和解决问题的方法。在结构分析方法中，只有某个未知变量出现在某方程，该变量才会被考虑。

表征系统模型的动态方程可用结构矩阵来表示：结构矩阵中横行代表M中的方程，列代表未知变量X。若xj∈X(j=1, ...,h)出现在方程ei∈M(i=1, ...,m)中,则结构矩阵第(i,j)处元素的值为1，否则为0。

利用Dulmage-Menelsohn(DM)分解可对结构矩阵进行行与列的置换，置换后的矩阵如图1所示。其中，白色区域的矩阵元素全为0，灰色区域则表示存在非零元素。

图1 DM分解后的结构矩阵Fig.1 Structural matrix after DM decomposition

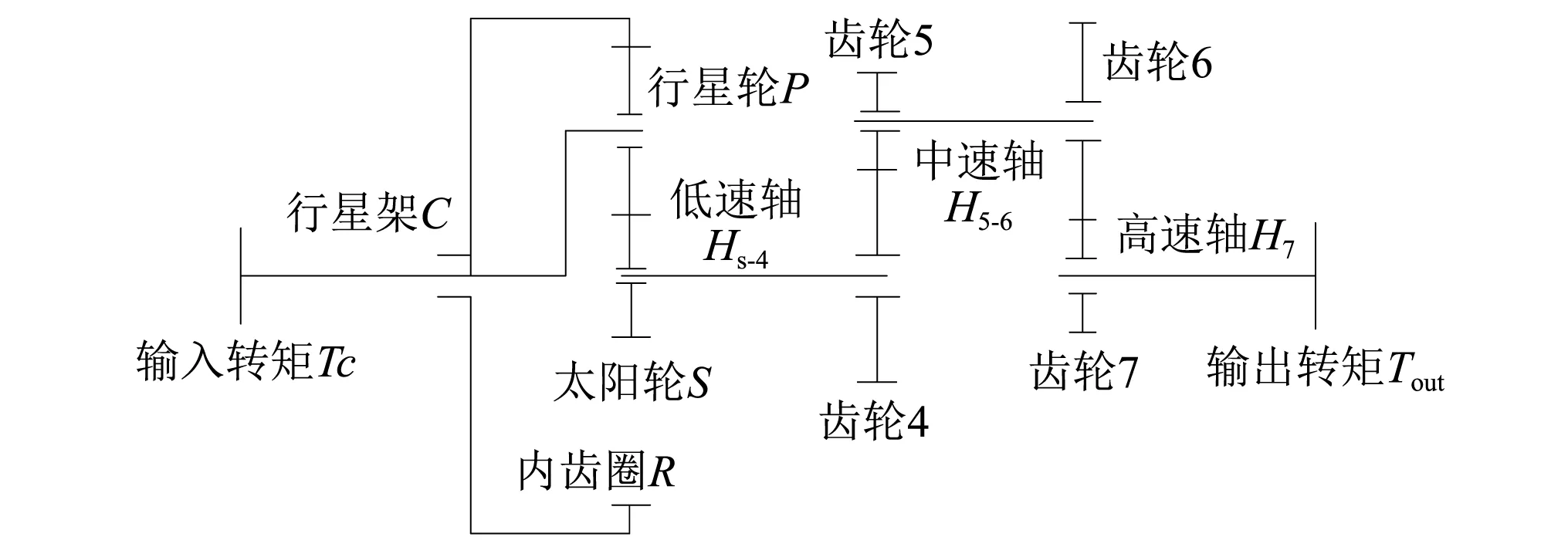
定义1每一对(Mi,xi)被定义为块bi。若DM分解后的结构矩阵中第(i,j)处非零，则认为从块bj到块bi间存在一条路径，并定义块之间高低顺序为bj≤bi，其中i

定义2如果集合S与集合簇C=(C1,C2, ...,Cl)的每个集合都存在着非空交集，那么集合S是集合簇C的碰集。

定理1若ef∈M+，则故障f在结构上是可识别的。其中，ef∈M是故障f∈F影响的方程。模型M的超定部分使用符号M+来表示。若某故障在结构上可识别，则该故障为可识别故障。

1.2 基于故障识别与隔离的传感器配置

在基于模型的故障诊断中，残差常被用来进行故障的识别与隔离。一般，残差可通过分析解析冗余关系(ARRs)来获得。在给定方程组M=(e1, ...,em)，未知变量X=(x1,x2, ...,xk)，已知变量Y=(y1,y2, ...,yv)的条件下，从方程组M中选取合适的超定方程组M+。由于M+中未知变量的个数小于方程的个数，因此，通过运算可消除方程M+中的所有未知变量，最终获得仅含已知变量的约束关系式r=f(y)[23]，即残差。在系统正常的情况下，残差r(y)=0，否则，残差r(y)≠0。以此来进行故障的识别与隔离。

对于某些故障，如果能够安装最少的传感器识别出所有这些故障，该传感器的配置集合就称为最小的传感器集合。在此基础上，我们研究能够将给定的故障相互区分开的最小的传感器集合，即能够实现最大故障隔离的最小传感器集合。

2 基于故障识别与隔离的风机齿轮箱传感器配置方法

2.1 最大故障识别条件下齿轮箱传感器配置

基于故障识别的风电机组齿轮箱传感器配置方法如下：

(1)依据风机齿轮箱的动态方程组M，构建风机齿轮箱的结构模型。该结构模型包括未知变量X的结构模型、给定故障集F={f1, ...,ft} (t为故障的个数)的结构模型和可测量变量P的结构模型。

(3)根据定理1，当传感器能够测量风机齿轮箱块bi(i=1,L,n)中的变量时，影响此块的故障就能够被识别。根据定理2，测量块bi(i=1,L,n)中的变量会添加测量方程e∶y=xi，所有满足bj≤bi的方程与测量方程e构成超定方程组。再由定理1可得结论：所有影响块∪j∶bj≤bi的故障均变得可识别。即只需测量齿轮箱结构矩阵块bi中的变量，便可识别影响块bi及∪j∶bj≤bi块中的所有故障。因此，测量结构矩阵最高块bmax中的变量，即可识别影响块∪j∶bj≤bmax中的所有故障[24]。

(4)在结构矩阵中，当结构矩阵第(i,j)处元素为0时，块bi与bj之间不存在大小关系。因而，在对所有块进行排序时可能出现多个块的大小排列序列。例如，对于一个含有4个块的结构矩阵，可能出现如下排序b1>b3,b2>b4，其中，结构矩阵第(1,2)，第(1,4)，第(2,3)，第(3,4)处元素为0，第(1,3)，第(2,4)处元素为1。最高块分别为b1,b2。因此，风机齿轮箱结构矩阵中的bmax也可能有多个。分别求出不同最高块所对应的最少传感器集合，并将这些对应于不同最高块bmax的传感器集合求取碰集，便获得最大故障识别条件下的最小传感器集合MS={y=xi},i=1,…,Θ，Θ为传感器个数。

2.2 最大故障隔离条件下的齿轮箱传感器配置

下面，给出风电机组齿轮箱在最大故障隔离条件下的传感器配置方法：

(1)将故障识别所获得的最小传感器集MS，添加到系统原来结构模型M={e1,...,em}中，得到新的结构模型M′=MS∪M。

(2)从故障f1开始，将故障f1所对应方程ef1从风机齿轮箱的动态模型中去除，获得新的结构模型M″=M′/ef1。然后，对故障模型M″继续进行故障识别，得到识别结构模型M″中所有故障的最小传感器集合S1。

由于传感器集合S1的添加，集合M″中的故障均可被识别。显然，ef1∉M″，自然ef1∉(M″)+，所以，故障f1在结构上是不可识别的。因而，故障f1和M″所包含的故障是相互隔离的。

(3)依次除去包含不同故障fk(k=1, ...,t-1)的方程并重复(2)，得到实现故障fk与除去fk后所有剩余故障相互隔离的最小传感器集合Sk，直至最低块。

(4)对除去不同故障fk所获得的最小传感器集合Sk,求碰集S，获得最大故障隔离条件下的最小传感器集合。

3 风电机组齿轮箱的结构模型

3.1 齿轮箱动力学模型

本文采用模型为1.5 MW风机，其齿轮箱为一级行星、两级平行结构，如图2所示。主要部件为行星轮内齿圈R、行星架C、3个行星轮Pi(i=1,2,3)、太阳轮S；平行齿轮系统的低速轴Hs-4、低速轴斜齿轮G4、中速轴H5-6、中速轴齿轮G5和G6、高速轴H7、高速轴齿轮G7。

图2 风机齿轮箱的机械结构Fig.2 Mechanical structure of wind turbine gearbox

3.1.1 行星齿轮传动的动力学模型

图3为行星齿轮传动的动力学模型。由系杆、太阳轮、内齿圈、行星轮等构件组成。各构件的参数取用不同的下标：系杆为c，内齿圈为r，太阳轮为s，行星轮为Pj(j=1,2,3)。

首先，建立行星轮系和两级平行轴斜齿轮传动的振动模型，然后对连接部进行适当的简化处理，将两部分连结起来，形成齿轮箱的动力学模型，其详细数学模型见附录。

图3 行星轮动力学模型Fig.3 The dynamics model of planetary gear

其中：xi,yi,θi(i=s,r,c,1,2,3)为振动构件i的质心偏离其理论的线位移与角位移；ri(i=s,r,1,2,3)为各齿轮的基圆半径；rc为行星轮中心分布圆的半径；ui=riθi(i=s,r,c,1,2,3)为由振动而产生的角位移折算到圆周上的线位移；φi=2π(i-1)/3(i=1,2,3),为第i个行星轮的理论中心到系杆的理论中心的连线与坐标轴x方向的夹角；kp为齿轮轴轴承的刚度；kp和kit(i=c,r,s)分别为中心构件的径向、切向支承刚度；mc,mr,ms,mp,Ic,Ir,Is,Ip分别为行星架、内齿圈、太阳轮、行星轮的质量与转动惯量。

3.1.2 两级平行轴斜齿轮动力学模型

斜齿轮传动系统的振动形态除具有弯曲振动、扭转振动和轴向振动外，还具有轴向动态啮合力使齿轮副产生扭摆振动。因此，其动力学方程为弯-扭-轴-摆多自由度振动。但由于水平、垂直方向的振动不便测量，而轴向振动易于测量，并且轴向振动为主要振动。在这种情况下，本模型只考虑轴向振动。斜齿轮副典型的轴向振动动力学模型如图4所示。每个齿轮(主、被动齿轮)具有2个自由度(1个轴向振动，1个转动)。

图4 两级平行轴齿轮动力学模型Fig.4 The dynamics model of two parallel shaft

其中：K45,K56分别为齿轮G4,G5和齿轮G6,G7的啮合刚度；K4s,K56z,K7分别为轴Hs-4、齿轮轴H5-6、轴H7的轴承轴向刚度；C45,C56,C4s,C56,C7为相应的阻尼；x45,x67分别为齿轮G4,G5和齿轮G6,G7沿啮合线方向的位移；θi,ri,Ii(i=4,5,6,7)分别为齿轮G4,G5,G6,G7的扭转振动位移、基圆半径、转动惯量；Z4s,Z56,Z7分别为轴Hs-4、齿轮轴H5-6、轴H7的轴向振动位移；β45,β67分别为齿轮G4,G5和齿轮G6,G7的螺旋角；m4s,m56,m7，分别为齿轮轴Hs-4,H5-6,H7的质量；α45,α67分别为齿轮G4,G5和齿轮G6,G7的压力角。

3.2 风机齿轮箱故障信息的引入

为简化问题，在进行风机齿轮故障分析时，进行以下假设：由于行星轮一直在做旋转运动，当故障发生时，只假定其中的一个行星轮发生故障，其余的正常；忽略加工和装配误差对动态方程的影响。

齿轮箱故障信息的引入，就是将相应的故障信息作为附加信息添加到动态方程中。本文重点分析轮齿故障，其他类型故障原理类似。在实际应用中，轮齿故障种类多、故障发生的概率各不相同。然而对于不同的轮齿故障，如点蚀和胶合故障，均会引起齿轮综合啮合刚度的变化。因此，在进行故障信息导入时，便以齿轮啮合刚度的变化来引入故障信息。这样可以在保证正确的前提下，使得包含故障信息的动态模型变得简单和直接。

轮齿类故障是引发齿轮传动系统故障的主要原因，所以轮齿的故障诊断是齿轮箱故障诊断的重点。在常见的齿轮故障类型中：齿的断裂故障所占的比例大约为41%；齿面疲劳(点蚀、剥落等)约占31%；齿面划痕约占10%；齿面磨损所占比例为10%；其他剩余的故障如齿面龟裂、化腐、塑性变形。

齿轮故障中所占比例最大的两种故障，齿的断裂和齿面疲劳，均会引起齿轮综合啮合刚度的减小。动态模型中故障的引入正是以此为依据：以太阳轮为例，当其发生诸如齿的断裂、疲劳等故障时，太阳轮与行星轮之间的齿轮综合啮合刚度ksn会变为(ksn)′=(1-fsn)ksn。此外，由于行星轮发生故障时，也会引起太阳轮与行星轮之间的齿轮综合啮合刚度发生变化，只是(ksn)′=(1-fn)ksn。因此，加入这两种故障信息后的齿轮综合啮合刚度变为(ksn)′=(1-fn)(1-fsn)ksn，如附录中的方程e7所示。其它齿轮故障信息的引入方法亦是如此。

在建模过程中会遇到如下问题：一个故障会在多个方程中出现，如方程e7和方程e16均会出现太阳轮的故障。在此，引入变量xfs，将所有方程中含有的太阳轮故障fs均用变量xfs代替。同时增加方程xfs=fs，即附录中的方程e27。其他故障均做同样处理，这样可以保证每个故障，只影响一个方程。

3.3 风机齿轮箱的可测未知变量

本模型中的未知变量包括支架C扭转振动位移θc，动坐标系中质心偏离其理论位置的线位移xc,yc，行星轮Pi(i=1,2,3)旋转振动位移θi(i=1,2,3)动坐标系中质心偏离其理论位置的线位移xi,yi(i=1,2,3)，太阳轮扭转振动位移θs，线位移xs,ys，内齿圈扭转振动位移θr，线位移xr,yr，低速轴轴向振动位移Z4s，齿轮G4,G5,G6,G7的旋转振动位移θ4,θ5,θ6,θ7，中速轴轴向振动位移Z56、高速轴轴向振动位移Z7。

3.4 风机齿轮箱的结构模型

在附录中，齿轮箱动态方程组记为E=(e1,e2, ...,e34)，方程变量分为已知变量集Y=(Tc,Ts,Tout)和未知变量集X=(xc,yc, ...,xf7)，所有故障构成的故障集为P=(θc,arx,ary,Z4s,Z7)，传感器可测变量集为，则风机齿轮箱的结构模型如图5所示。

图5 风机齿轮箱的结构模型Fig.5 The structural model of the turbine gearbox

4 仿真与应用实例分析

4.1 最大故障识别条件下的风机齿轮箱最小传感器集合

图6 DM分解后的齿轮箱结构模型Fig.6 Structual model of turbine gearbox after DM decomposition

由图6可以看出，DM分解后风机齿轮箱结构模型中的块分别为b1～b11。块b1为方程e26中的变量arx，记为b1{e26(arx)}。剩余的块可分别表示b2{e27(ary)}b3{e1(xc,yc,x1, ...,x2), ...,e18(xc,yc,x1, ...,x2)}，b4{e19(Z4s,θs, ...,Z7), ...,e25(Z4s,θs, ...,Z7)}，b5{e28(xf1)}，b6{e29(xfs)}，b7{e30(xfr)}，b8{e31(xf4)}，b9{e32(xf5)}，b10{e33(xf6)}，b11{e34(xf7)}。

所有块的排列顺序为：{b1,b2}>b3>{b5,b6,b7}，b4>{b8,b9,b10,b11}。此时，最高的块为{b1,b2}和{b4}。由于b5,b6,b7分别包含的故障信息为b5{e28(xf1)}，b6{e29(xfs)}，b7{e30(xfr)}，所以要识别故障{f1,fr,fs}，只需要测量块{b1,b2}中的变量即可，即可测量变量{arx,ary,θc}；类似地，为了识别块{b8,b9,b10,b11}中的故障{f4,f5,f6,f7}，只需测量块b4中的变量{Z7,Z4s}。

若要识别所有故障，只需同时测量块{b1,b2}与块{b4}中的变量即可。块{b1,b2}中传感器可测量变量为{arx,ary,θc}，块{b4}中的传感器可测量变量为{Z7,Z4s}。所以对最高块对应的可测量变量集合取碰集即为识别所有故障的最少传感器集合。因而，识别所有给定故障的最小传感器集合为：可测量变量集{θc,Z4s}，{θc,Z7}，{Z7,arx}，{Z4s,arx}，{Z7,ary}，{Z4s,ary}，任意一个。

4.2 最大故障隔离条件下的风机齿轮箱最小传感器集合

在安装传感器可识别所有故障后，还需确定所安装传感器是否能保证各故障可隔离。本例以添加测量变量{Z7,arx}的传感器集合来说明进行故障隔离的过程。

在增加测量变量{Z7,arx}的传感器后，原方程组添加测量方程y1=Z7，y2=arx。结构模型随之相应变化，结构矩阵增加两行，其中变量arx,Z7处的值为1，其余元素为0，获得新的结构模型M0。

以故障f1为例，实现最大故障隔离过程如下：在结构模型M0中，除去包含故障f1的方程，获得新的结构模型M″=M0/ef1。计算识别结构模型M″中所有故障的最小变量测量集合。计算结果为变量测量集合{θc}或{ary}。添加该变量测量集合后，M″中的故障均可被识别。而ef1∉M″，自然ef1∉(M″)+。所以，故障f1不可被识别。由此，故障f1可与M′包含的所有故障相互隔离。

除去不同故障后，识别相应剩余故障需添加的最小变量测量集合如表1所示。

表1 去除不同故障后识别剩余故障的变量测量集合Tab.1 The sensor sets of identifying all remaining faultsafter removing the specific fault

4.3 应用实例分析

文献[25]中研究了利用EMD(Empirical Mode Decomposition)识别风机齿轮箱中高速轴齿轮点蚀故障的方法，其齿轮箱结构与本文中探讨的齿轮箱结构相同，包含一级行星、两级平行齿轮。由于不能准确定位齿轮箱哪个部位发生了故障，为了最大程度捕获有效振动信息，在齿轮箱中从低速轴到高速轴依次安装了4个加速度传感器来测量振动信号。其中，1号传感器位于齿轮箱中行星轮上方部位，对结构模型中变量{arx,ary,θc}敏感；2号传感器位于高速轴齿轮G7的上方，可最大程度捕获结构模型中变量{Z7}的信号；3号传感器位于高速轴中部对应的上方齿轮箱，不能直接有效的捕获高速轴齿轮或高速轴的振动信息；4号传感器位于高速轴轴承上方，可有效捕获高速轴的振动信号，对应结构模型中变量{Z4s}。

利用EMD方法对4个传感器捕获的振动信号进行分析，发现2号和4号传感器故障特征明显，均指向高速轴齿轮，经分析可确定为高速轴齿轮对点蚀故障；而1号传感器信号未体现任何故障特征，3号传感器呈现了微弱的故障特征。这与结构模型的分析是一致的：为了识别高速轴齿轮故障{f4,f5,f6,f7}(文献[25]中出现了故障f7)，最优选择为{Z7,Z4s}中任一传感器(分别对应2号与4号传感器)；而1号传感器测量变量{arx,ary,θc}，适于发现行星轮部分故障{f1,fr,fs}；3号传感器安装位置不合理，不能最大程度体现某个部件的故障信息，但因为其靠近2号与4号传感器位置，因此得到微弱的故障信号。

通过上例证明了基于结构分析方法对风机齿轮箱齿故障识别的有效性，对实际工程中传感器配置有指导作用，工程师可根据实际情况有效合理地选择传感器配置方案。

5 结 论

本文基于结构分析方法，对风力发电机齿轮箱的传感器配置进行了研究。经过建模分析，得到了识别与隔离所有给定故障的传感器配置集合。基于结构分析方法的风机齿轮箱传感器配置有如下特点：

(1)风机齿轮箱的动力学方程为非线性的微分方程，变量多，计算复杂。而结构模型可对风机齿轮箱动力学模型进行简约化表示，使得非线性解析方程可以被高效地处理，极大简化了基于模型的传感器配置研究。

(2)传感器的配置多在系统设计初期进行，动态方程中的参数不易获得。采用结构分析方法解决传感器的配置问题，无需考虑方程中具体的参数值，因而具有极好的实用价值。

(3)由于结构分析方法是基于动态模型来进行故障识别与隔离，与基于数据分析的故障识别和隔离相比，定位故障发生的部位与类型的准确性和可靠性更高，而且更切合实际。

(4)结构分析方法可提供适合各种情况的灵活配置方案。如仅需识别或隔离某一个或几个故障，都可以改变参数进行分析，最终得到需要的传感器配置方案。

附录

行星架

kcxc=0

(1)

kcyc=0

(2)

uc]+kctuc=-Tc/rc

(3)

内齿圈

sinφrn+(yr-yn)cosφrn+ur-un]sinφrn+krxr=0

(4)

sinφrn+(yr-yn)cosφrn+ur-un]cosφrn+kryr=0

(5)

(yr-yn)cosφrn+ur-un+ern(t)]+krtur=0

(6)

行星轮

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(yr-y3)cosφr3+ur-u3]=0

(15)

太阳轮

sinφsn+(ys-yn)cosφsn+us+un]sinφsn+ksxs=0

(16)

(17)

(ys-yn)cosφsn+us+un]+kstus-Ts=0

(18)

cosβ45x45=Ts

(19)

(20)

(21)

(22)

(23)

(24)

(25)

xf1=f1

(26)

xfs=fs

(27)

xfr=fr

(28)

(29)

(30)

xf4=f4

(31)

xf5=f5

(32)

xf6=f6

(33)

xf7=f7

(34)

x45=(rb4θ4+rb5θ5)cosβ45-(Z4s-Z56)sinβ45

(35)

x67=(-rb6θ6-rb7θ7)cosβ67-(Z56-Z7)sinβ67

(36)