流线型箱梁断面的非线性颤振幅值特性研究

朱进波， 郑史雄， 唐 煜， 郭俊峰

(1.西南交通大学 土木工程学院 桥梁工程系，成都 610031；2.西南石油大学 土木工程与建筑学院，成都 610500)

桥梁颤振是一种自激发散振动，该振动现象会导致桥梁整体毁灭性的破坏。当前的颤振理论体系[1]已基本可以准确预测桥梁的颤振临界风速。该风速预测方法是建立在结构微幅振动的线性颤振理论框架[2-3]下，即桥梁颤振导数与断面振幅无关，求得的颤振临界风速具有明确的数值意义。在该风速后桥梁将直接作发散运动，在该体系之下并没有研究颤振后状态。

近年来随着材料科学、结构分析技术及施工方法的进步，桥梁结构逐步向大跨、轻柔化发展，悬索桥逐渐成为大跨度桥型的首选。而桥梁跨度的增长使得桥梁刚度和阻尼急剧下降，桥梁结构对风的敏感性增加，想要满足颤振设防规定需要大幅增加建桥成本，可以预见风对大跨度桥梁结构[4-6]的作用将逐渐成为提高桥梁跨径的主要制约因素之一。

基于风洞试验研究，Scanlan等将颤振导数表示的非定常气动自激力引入振动平衡方程中，摒弃了流固耦合的直接求解，建立了经典的颤振框架模型，采用半逆解法进行颤振求解。Wilde等[7-8]采用二自由度的状态空间复模态特征值求解方法(Complex Eigenvalue Analysis, CEVA)，其基本思想是将二维颤振问题转变为求解复特征值问题，以某阶模态下的阻尼比为零时，作为系统发散的依据，对应的风速为颤振临界风速。基于该框架下的解具有明确的数学意义，当风速超过这一临界点桥梁断面的振幅将指数级增加而出现发散，可实际现象中却并非如此。朱乐东等[9]在风洞试验中发现，一些钝体断面颤振发生后并不会出现如线性理论预测的那样，振幅按指数级迅速增长，而是由于自激力的非线性效应稳定在一定幅值状态。学者们开始关注桥梁进入颤振后的真实运动状态，颤振研究逐步走向精细化。

想要弄清桥梁颤振后的特征并非易事，徐旭等[10]建立一个关于纯扭转颤振的非线性气动力模型，研究桥梁颤振的非线性稳定性问题；张朝贵[11]引入范德波尔方程来试图解释软颤振现象；王骑等[12-13]将桥梁颤振形态转变为单自由度扭转方程，分别描述了极限环与软颤振现象，反映了阻尼比与气动力的非线性特性。尽管许多学者做了大量的研究工作，鉴于非线性问题的复杂性，对桥梁颤振后的特征状态依然没有定论。目前对于非线性自激力的探索主要集中在气动力随振幅的非线性变化规律与气动本身的高次谐波特性两个方面。

对于桥梁颤振后的振动状态，最为关心的便是桥梁振动幅值与风速的关系。张彦等[14-15]分别从数值模拟和风洞实验方面对不同振幅下桥梁断面自激力进行研究。唐煜[16]基于传统颤振耦合理论，发展出非线性二维两自由度耦合颤振分析方法。

本文基于气动自激力随振幅响应变化这一思想，依托颤振理论框架和求解思路，提出更加规范、精细的考虑颤振幅值因素的二自由度复模态特征值求解方法。基于此方法，提出非线性颤振幅值响应搜索程序，一定程度上揭示了桥梁颤振后的特征状态。

1 流线型箱梁断面的颤振研究方法

随着大跨度桥梁不断的投入建设，为满足其气动稳定性需求，流线型箱梁断面型式逐渐成为大跨悬索桥主梁断面型式的首选。目前主要采用直接风洞试验法和基于风洞试验识别参数的理论分析法来检测桥梁的颤振稳定性能。如今伴随着流体力学与计算机硬件的发展，数值风洞识别气动参数的方法逐渐被接受与认可，其纯理论的计算方法有望代替物理风洞试验方法。该方法可分为三个部分，即自激气动力模型、颤振导数数值识别和二维耦合颤振分析方法，全部过程都是数值计算。

选取Scanlan等的经典颤振理论框架作为自激气动模型

(1)

(2)

基于此方法，本文以某大跨度悬索桥为研究对象，研究其颤振幅值特性，该桥梁结构基本参数如表1，流线型箱梁断面尺寸如图1所示。

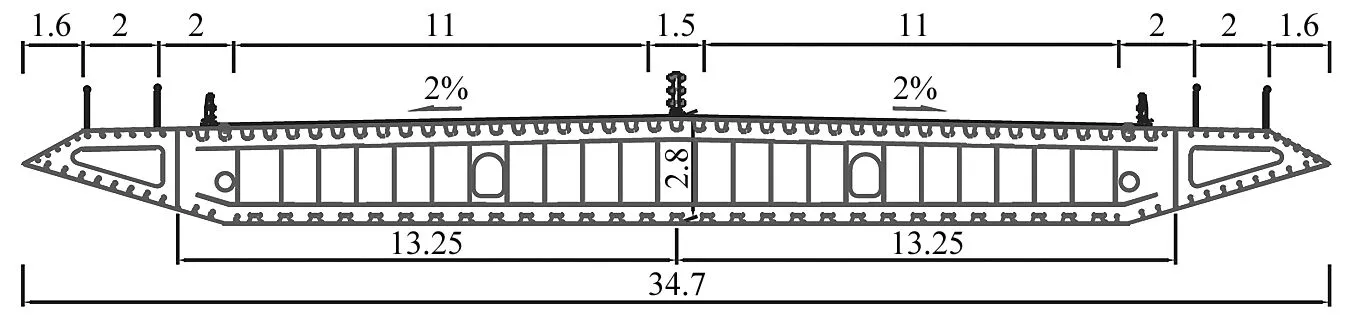
图1 主梁断面图Fig.1 Section diagram of the main beam

表1 桥梁结构基本参数Tab.1 Basic parameters of the bridge structure

2 气动参数识别

基于Fluent软件，建立二维数值风洞模型，通过著名的N-S方程实现对流体时间域和空间域的控制，采用SSTk-ω湍流模型，实现数值模拟。应用强迫振动法[17]精确控制桥梁断面运动，采用具备非线性弹簧效果的多变形子区域动网格方法更新网格。

2.1 自激气动力分析

桥梁断面按缩尺比1∶40建模，竖向振动幅值选取区域为0.001B～0.14B(B=0.867 5 m)，扭转振动幅值选取区域为0.1°～30°。选定一振动幅值，分别对断面赋予单频单一自由度强迫振动，每个振幅下的折算风速选取区间为2～10，来流风速取为20 m/s，计算出相应的自激气动力，具体的工况设置如表2所示。

表2 工况设置Tab.2 Operation setting

通过对各折算风速状态下的自激气动力进行频谱分析，可以研究气动力随幅值变化的气动规律。由于算例桥主梁的颤振临界风速约为66.3 m/s，振动频率约为0.285 Hz，相应的折算风速约为6.7左右，限于篇幅，本文以折算风速为6的状态为例，分析其气动频谱特性。

首先列出流线型箱梁断面0°攻角时在单频竖向振动下的部分气动力频谱分析图(去除静力分量)。

由图2和图3可以看出，当箱梁断面做单频单一竖向振动时，产生的自激力频谱中除了包含与振动频率同频的基频分量外，还会有些许频率是断面振动频率整数倍的高次谐波分量。在气动力成分占比中，基频谐波成分明显，尽管随着振幅增大高次谐波占比从无到有，但是与基频成分相比很小，几乎可以忽略。

图2 单频竖向不同幅值振动下的气动升力频谱图Fig.2 Aerodynamic lift spectrum under different vertical amplitude vibrations of the single frequency

图3 单频竖向不同幅值振动下的气动扭矩频谱图Fig.3 Aerodynamic torsional spectrum under different vertical amplitude vibrations of the single frequency

接着列出流线型箱梁断面0°攻角时在单频扭转振动下的部分气动力频谱分析图。从图4中可以看出，与单频单一竖向振动相同，单频单一扭转振动下也会产生以基频为主、整数倍频掺杂的多频气动力。当振幅增大时，二次倍频占比开始明显，三次倍频谐波及更高次谐波占比可以忽略。随着幅值再次增大，更高次波成分逐渐显露。

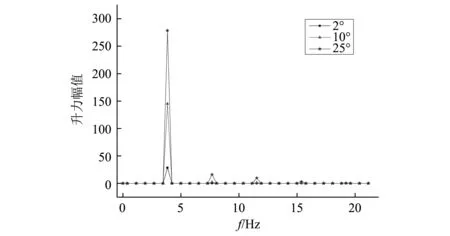
图4 单频扭转不同幅值振动下的气动升力频谱图Fig.4 Aerodynamic lift spectrum under different torsional amplitude vibrations of the single frequency

为分析高次谐波的成分，调整竖向坐标为对数坐标，给出升力幅值频谱图。如图5所示当振幅从2°-5°-18°时，三次谐波分量愈发明显，其占比逐渐超越了二次谐波，三次谐波的重要性在大振幅振动中显现出来。这与王骑的试验结果是吻合的。对于产生的升力或者力矩，随振幅的变化规律是同步的。

图5 单频扭转不同幅值振动下的气动升力频谱图(对数坐标)Fig.5 Aerodynamic lift spectrum under different torsional amplitude vibrations of the single frequency

综上分析，在单频单自由度振动时，箱梁断面会产生非线性气动力。随着振幅的增大，倍频气动力占比逐渐增大，其复杂的特性规律难以捕捉。同样，气动力随幅值的变化规律再也不能用“线性关系”简单描述， 相应的通过气动力识别的颤振导数则不再随振幅微幅变动。

2.2 非线性颤振导数

用最小二乘拟合[18]识别出随折算风速与振幅变化的非线性颤振导数，通过插值得到的三维曲面图，见图6。

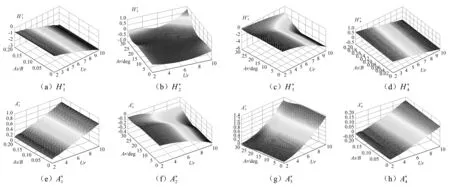
图6 颤振导数曲面Fig.6 Flutter derivative surface

那么当实际风速跨过传统线性理论预测的颤振发散风速时，振动幅值指数倍增大，因断面的气动参数的非线性变化，桥梁断面的系统振动阻尼可能由负转正，振动又趋于平稳。

3 复模态特征值求解方法

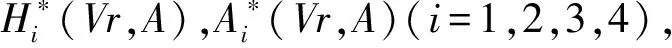
为了简化公式的形式且更直观地说明，将自激力进行符号表示简化

式中，Hi，Ai(i=1,2,3,4)是有量纲的颤振导数，它们是因子与颤振导数合并的结果，同样其也仅和折算风速与振幅有关。代入式(1)和式(2)中

(3)

用矩阵记号，将式(3)改为

(4)

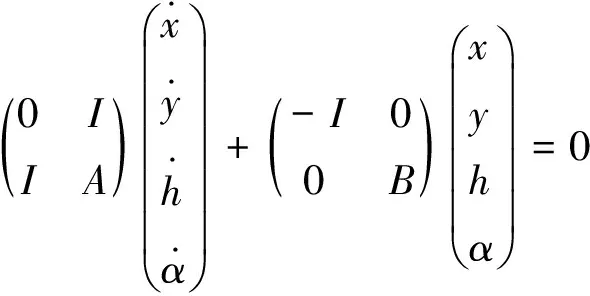
(5)

那么就转变成著名的状态方程，向量(x,y,h,α)T称为状态向量，因为它能唯一确定二自由度的运动状态。式中每个子矩阵都是2×2矩阵，0表示零矩阵。

因为颤振临界状态时结构处于等频运动状态，因此可以设

(6)

式中，ω应为实数。将式(6)代入式(5)得

(7)

注意对任意的eiωt，式(7)都是满足的，于是应有

(8)

为了使式(8)有非零解，那么其系数行列式必须等于零。式(8)的系数行列式是一个关于ω的四阶方程，称为特征方程。该方程中有两个未知数ω与U，如果不考虑颤振振幅因素的影响，不妨代入一组微振幅下的颤振导数，通过将试探的风速值代入系数矩阵中，并调用复系数矩阵特征值算法，得到ω的四个根，一旦某一个根是实数，那么此ω为颤振临界状态下结构的振动频率，对应的风速为临界风速，如上所述，求解此特征方程的方法是一个逐步搜索的过程。

则系统在颤振临界状态之前的任意状态、任意时刻的运动方程可表示为

(9)

当系统以某阶复频率做主振动时(r=1 or 2)，振动系统的周期表达式为

(10)

根据欧拉公式变换为

(11)

竖向与扭转振动相位角

(12)

竖向与扭转振动幅值比为

(13)

此处绝对值为模的概念。

值得注意的是，选取任意一组微幅振动下的颤振导数代入计算后，在达到了颤振临界状态时，会得到式(13)中幅值比一值。由于考虑了颤振振幅响应因素，应满足代入的颤振导数对应的幅值比与临界状态的幅值比相同。故之前代入的一组颤振导数只能称作是一种试探，因此不断调整试探振幅使得其满足上一结果的幅值比，如此往复，直到代入的颤振导数对应的幅值比与求解的幅值比相同为止，即为颤振的最终状态。上述方法称为考虑颤振振幅因素的二自由度复模态特征值求解方法。其求解流程图如图7所示。

图7 改进的复模态特征值求解方法流程图Fig.7 Improved flow chart of complex modal eigenvalue solution method

需要说明的是，由于无法预知颤振时起振的具体幅值，故而依旧只能选取微幅概念中的某一幅值，保持某一自由度振幅不变，不断改变另一振幅来满足弯扭幅值比的要求。本文研究对象为流线型箱梁断面，并且其扭弯频率比为2.13，很有可能发生颤振时为扭转驱动机制。为研究方便，故而将扭转振幅作为不变量。需要强调的是，对于求得的最终状态对应的振幅，无论假设竖向或扭转幅值为不变量，选取另一变量的任意振幅值作为初始试探值，最终状态的结果都是趋于一致的，即初值的改变只会影响搜索路径。

4 颤振后状态探索研究

4.1 颤振临界风速求解

假设颤振时扭转振幅为0.1°，结合上述求得的颤振导数曲面图，基于考虑颤振振幅因素的二自由度复模态特征值求解方法，得到颤振临界风速为66.34 m/s。为了使本文的方法更具有说服力，选用断面结构类似的南京四桥主梁断面进行验证。将唐煜研究中运用同种方法求得的三维颤振导数代入计算，得到扭转角1°微幅振动下的颤振临界风速为70.4 m/s，这与文献[19]中用直接风洞实验法测得的风速70.8 m/s十分接近，除了反映颤振导数计算的合理性、基于风洞试验识别参数的理论分析法适用性外，也充分说明了考虑颤振振幅因素的二自由度复模态特征值求解方法是准确的。

4.2 颤振后的振动状态可能性假设

一旦来流风速超过临界风速，系统的气动扭转阻尼为负，桥梁断面作发散运动，振幅随之增大，相应的气动自激力的高阶成分逐渐显现，气动参数的非线性特性愈发显著。桥梁断面周围的气动环境随着振幅变化而改变，那么就极有可能出现再次稳定的现象。如风洞试验中的软颤振现象，就可以从某方面说明气动参数随振幅的变化导致起振后断面仍然陷入环振荡现象。

合理的气动力与振动方程搭接方法、合适的气动参数识别方法都使得建立非线性颤振框架模型困难重重。为了在现有的颤振框架下进行颤振后状态的有益探索，故而结合塔克马桥风毁工程实际事件、软硬颤振风洞实验现象，假设桥梁颤振的最终形态都为同一频率的简谐扭转和简谐竖向的耦合运动。那么在该假设下，对颤振后桥梁断面振动形态进行稳态响应设想：当风速达到颤振临界风速时，桥梁断面作简谐平稳运动；一旦越过临界风速，系统阻尼由零转负，桥梁断面做发散运动；随着振动幅值增大，桥梁断面气动环境发生改变，在某一振动幅值下，系统阻尼由负转正之际，桥梁振动形态又趋于稳定；当风速继续增长到某一值，系统阻尼由正转负，在上一稳定振幅下又会出现简谐振动稳定状态；再次越过上一稳定风速，断面又将做发散运动；当断面幅值不断增长，系统阻尼再也不能由正转负时，桥梁断面也就一直发散振动直至破坏。

尽管上述假设将颤振发生过程中的非线性行为描述弱化为简谐环振动现象，但是简谐环振动假设可以帮助我们认知非线性气动弹性响应的一些规律，挖掘出主要相关的气动因素。

4.3 颤振幅值响应特性分析

根据上述设想，研究颤振后的振动状态，基于考虑颤振幅值因素的二自由度复模态特征值求解方法，给出非线性颤振幅值响应搜索程序流程图，如图8所示。

图8 非线性颤振幅值响应搜索程序流程图Fig.8 Flow chart of the search program for nonlinear flutter amplitude response

在颤振幅值响应风速搜索过程中分为整体风速与内部风速，设置内部风速的目的是便于程序整体编译，整个内部风速搜索可以视为一个子程序，整个风速搜索过程需遵循以下步骤：

步骤1设定基本参量如初始风速、初始频率、起振微小扭转与竖向振幅和最大限定扭转角等，选定整体风速初始值；

步骤2进入内部风速搜索，微幅等距增长风速值，迭代计算指定振幅下的系统频率和阻尼，每阶风速后都需判定该阶下的系统阻尼，若系统阻尼由正转负且弯扭比合适，则停止内部风速搜索，每一个完整的子程序搜索过程的最终风速作为本次的内部风速值，记录相应参数值；

步骤3转入整体风速搜索，若内部风速搜索值小于或等于整体风速值，则认为颤振发生，并记录当前风速，否则增长整体风速，转入步骤2，若整体风速达到限定最大风速值则停止搜索；

步骤4一旦颤振发生，保持整体搜索风速不变，由于此时的系统阻尼为负，断面作发散振动，等距微幅增长扭转角，并结合上一扭转角于颤振时的弯扭比计算出当下的竖向振幅试探值，转入内部搜索子程序中，记录相关参数，转入整体风速搜索，若扭转角大于限定的扭转角上限值则停止搜索；

步骤5当内部风速搜索值小于或等于整体风速值时，则继续增大振幅转入步骤4计算；

步骤6当内部风速搜索值大于整体风速值时，记录此时的振幅参数，保持振幅不变，增长整体风速，进入内部搜索程序，当整体风速不小于内部风速时，转步骤3。

需要注意的是，对一个参数的计算和迭代求解都是在指定的振幅条件下进行的。本文中增加了弯扭幅值比的概念，为了便于程序的整体编译，设置了内部风速搜索。内部风速仅具有比较作用，当内部风速大于整体风速时，其意义为在当前整体风速下，桥梁断面于指定幅值条件振动下系统阻尼为正；当内部风速小于整体风速时，桥梁断面的系统阻尼为负。故而运行上述程序进行求解，结果如图9所示，其前段以红色圈标注的细部图如图10所示。

图9 颤振振幅响应总体图Fig.9 Whole graph of flutter amplitude response

从图10中可以看出，设定的起振扭转角为0.1°，当越过颤振临界风速66.34 m/s后，桥梁断面的振幅响应并不是直接发散的，而是随着风速的增长爬坡式的增大，扭转角从0.1°，-0.6°，-0.9°，-1.5°，-1.8°，-2.1°，-2.4°，-2.7°缓缓增大。当越过风速66.42 m/s时，桥梁断面振幅响应出现了阶跃性变化，扭转角从2.7°陡增到19.6°，两个极限稳态间的风速间隔约0.1 m/s，一旦越过风速66.49 m/s，如图9所示，颤振振幅响应又陷入了爬坡式的增长，直到风速越过75.61 m/s后，随着振幅的增长，断面再也达不到稳态响应。

图10 颤振振幅响应局部图Fig.10 Local graph of flutter amplitude response

图11 颤振响应弯扭幅值比Fig.11 Crankle amplitude ratio of flutter response

图12 颤振响应相位角Fig.12 Phase angle of flutter response

该桥型断面与大多流线型断面类似，都是以扭转形态为主的颤振机制，在颤振振幅响应搜索中，如图11、图12所示，起始的弯扭振幅比几乎区别不大，当越过风速66.49 m/s时，弯扭比陡增至14.2，之后相位角呈现先增加后减小的趋势，扭转运动的幅度比例增大，扭转与竖向运动的相位角不断缩小，桥梁断面的运动形态逐渐向单一自由度逼近。

5 结 论

本文基于风洞试验识别参数的理论分析法，计算了流线型断面的三维颤振导数曲面、改进了传统的复模态特征值求解流程和建立了非线性颤振振幅响应搜索程序。

(1)通过控制振动幅值识别出不同振幅下的气动力，单频单自由度振动下桥梁断面气动力会有非线性成分，随着幅值增大，非线性成份比重扩大，单频单一扭转运动下尤其明显。值得注意的是在扭转运动下，当振幅达到某一值时，三次谐波力占比超越了二次谐波力。

(2)通过最小二乘拟合识别出随振幅与折算风速变化的颤振导数，并通过插值绘制成三维曲面。对于流线型箱梁断面而言，颤振导数H1,H4,A1,A4变化不大，而A2,H3则变化显著，一定程度上反映了气动力随振幅改变的非线性性质。

(3)发展传统的颤振理论，引入弯扭幅值比概念，扩展出考虑颤振振幅因素的二自由度复模态特征值求解方法，并通过实桥算例证明了该方法的准确性与适用性。

(4)编译非线性颤振振幅响应搜索程序，给出了微幅颤振后的状态。流线型箱梁发生颤振后，振幅会出现阶跃性增长，达到某一大幅值后，又基本处于振幅缓增的振动状态。

本文从颤振响应振幅入手，试图揭示颤振后的非线性动力学行为，对颤振后状态进行了尝试性的描述与分析。