电容式电磁驱动器非线性系统主共振分析
杨志安, 冯 浩
(1. 唐山学院和唐山市结构与振动工程重点实验室,河北 唐山 063000;2. 华北理工大学 机械工程学院,河北 唐山 063210)
电磁驱动器是一种重要的执行器,相比于传统驱动器,具有噪声小、精度高、长寿命等优点。已经越来越广泛的应用到各个领域,如磁悬浮列车[1]、电磁驱动泵[2]、航母电磁弹射[3],电磁激振器[4]、电磁传感器[5]等。然而,电磁驱动器工作过程中的振动,尤其是非线性振动,严重影响其性能,为了改善振动影响,对其进行深入理论研究就显得非常重要。
文献[6]利用数值方法研究了考虑轨道非线性的多车体磁悬浮列车系统的动力学行为,给出了轨道对三车体磁悬浮列车系统与对单车体系统的动力响应。文献[7]以环形极板为研究对象,应用多尺度法分析了该强非线性系统的主共振问题。文献[8]应用多尺度法得到了其模型在有界窄带随机激励下的一次近似解,导出系统的Ito随机微分方程,并分析扬声器静圈系统参数对主共振响应曲线和均方值的影响。
在众多的驱动器研究中,学者们集中研究的电磁驱动器系统的移动形式多为非线性移动。然而对于直线运动形式的研究却非常少。由于直线运动行程便于测量与控制,本文改进设计一种新型电容式电磁驱动器,该驱动器是驱动电容两极板之间介质板: 通过改变激励电压值,使介质板在两极板之间做直线运动。之后研究简谐激励下的电磁驱动器的非线性振动系统,根据拉格朗日麦克斯韦方程,建立非线性动力学模型,采用多尺度法对系统的主共振进行求解,并应用数值法验证分析系统各参数对振幅和共振区域的影响。
1 电容式电磁驱动器非线性动力学方程
电磁驱动器原理是将电能转换成机械能,是典型的机电耦合系统,可以将其简化成如图1所示的模型。
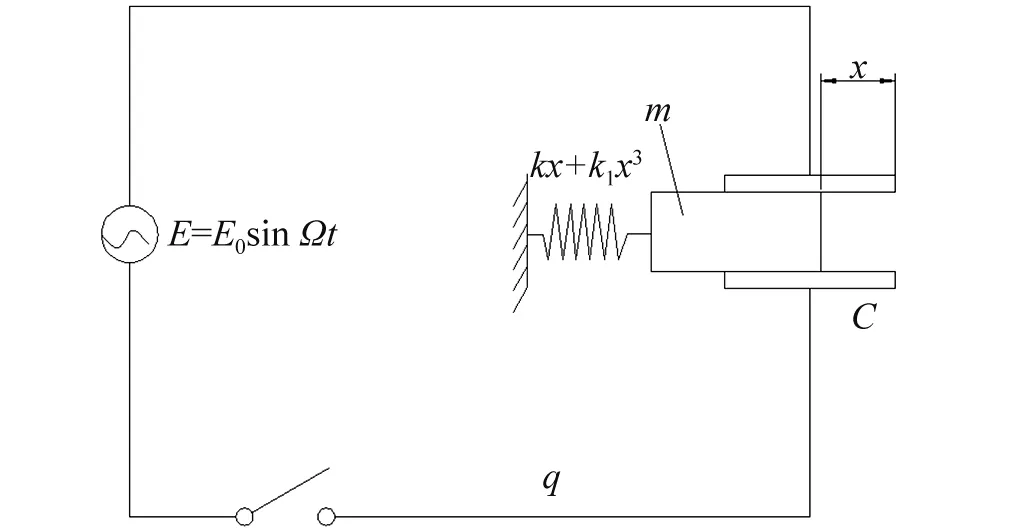
图1 电磁驱动器简图Fig.1 Electromagnetic drive diagram
通过改变激励电压,电容极板电压改变,通过极板上的静电驱动介质板直线运动。以电容介质板某一平衡位置为原点,选择介质板位移x和电量q为广义坐标。
1.1 作用于平行板电容器中介质板上的水平电磁力Fx[9]
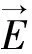
(1)

(2)
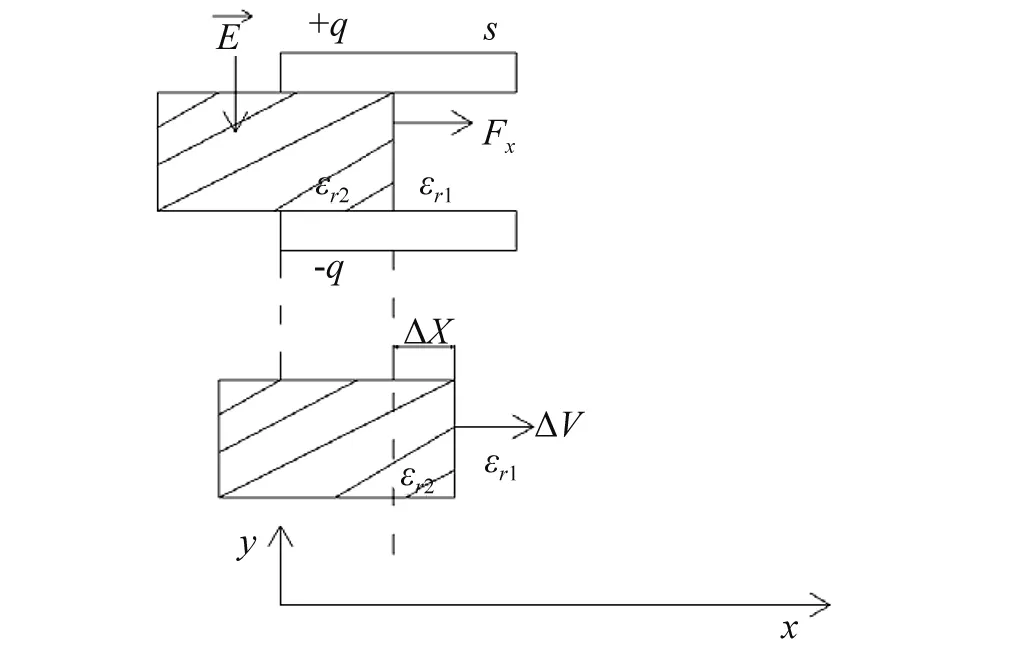
图2 电磁力Fx模型Fig.2 Fx model of electromagnetic force
则施加于薄层的总电场力为
(3)
1.2 计算平行板电容器的电容C
变介质电容器模型如图3所示,L0,b0分别为极板的长度和宽度;d0为介质板的厚度;x为介质板运动的位移。当极板中介质为空气时电容为
(4)
式中:ε0,εr1分别为真空和空气的介电常数。
图3表示2个电容器的并联,总电容为
(5)
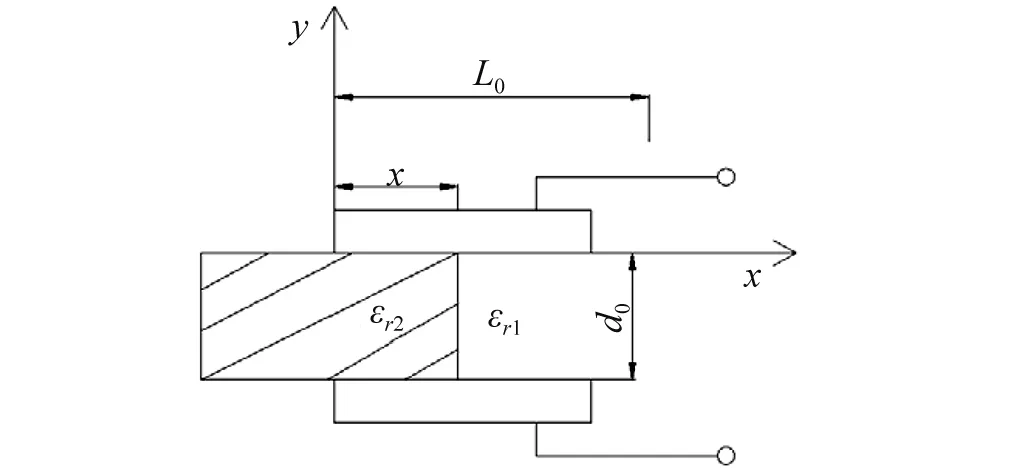
图3 变介质电容器模型Fig.3 Variable dielectric capacitor model
1.3 非线性振动方程建立
计算系统动能T、势能V、电场能We, 引入系统拉格朗日函数L

(6)
损耗函数为
(7)
非保守广义力

(8)
根据拉格朗日麦克斯韦方程[10]建立其非线性动力学方程
(9)
式中:m,d0分别为介质质量、厚度;k,k1分别为弹簧的线性和非线性刚度;L0,b0分别为电容极板的长宽;S为电容横截面积;E为激励电压。
由式(9)第一式可知,该式是关于电量q和位移x的机电耦合方程,第二式也是关于电量q和位移x的机电耦合方程,两个式子之间又通过电量q相耦合,将第一式中的q代入第二式中可得系统的振动方程。
2 简谐激励主共振分析
联立式(9)中的两式,将式(9)中第一式(q=EC)代入第二式,化简得
(10)
其中,
式(10)形式上是杜芬方程,实际它是机电耦合的,其激励与外加电压、电容器的几何尺寸和介质板的特性有关,以下分析系统的主共振。
所谓主共振是指激励频率ω接近派生系统固有频率ω0是产生的振动。如果系统是线性小阻尼系统,很小的激励幅值F就能激发强烈的工作。因此,研究主共振时对阻尼项、外激励幅值、非线性项都加以限制,在其前面冠以小参数ε,对式(10)进一步整理得
(11)
应用多尺度法[11]研究一次近似解,设系统(11)具有如下形式的解
x(t)=x0(T0,T1)+εx1(T0,T1)
(12)

将式(12)代入式(11),并利用导数算子表达式,比较ε同次幂的系数,得到一组线性偏微分方程
(13)
(14)
式(13)的解为
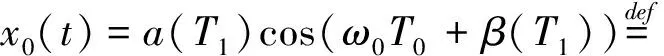
(15)
式中:cc为前面所有项的共轭。
引入
㊶Akhil Gupta,“Blurred Bourdaries:The Discourse of Corruption,the Culture of Politics,and the Imagined State”,American Ethnologist,22(May 1995).
(16)
分析系统主共振问题,也就是激励频率与固有频率接近时发生的共振,故设ω≈ω0, 还需引入调谐参数σ,得
ω=ω0+εσ,σ=O(1)
(17)
式(17)是系统发生主共振的频率条件。
将式(15)、式(17)代入式(14)可得消除长期项的条件
(18)
将式(16)代入式(18),进行化简分离其实部和虚部得
(19)
式中:φ=σT1-β。
式(19)上下两式联立可解出a,φ,可得式(11)的一次近似解
x(t)=a(T1)cos(ωT0+φ)+O(ε)
(20)
由稳态系统可知D1a=0,D1φ=0, 则式(19)变为
(21)
X1a6+X2a4+X3a2+X4=0
(22)
其中,
式(22)是关于a2的一元三次方程,根据确定性非线性振动理论,稳态解稳定的充要条件是
(23)
式(23)说明系统主共振稳态解与调谐参数有关,说明对于系统主共振的幅频响应方程式(22),在一定的区域内,系统可能存在三个稳态解,这些稳态解并不都是稳定的。
考虑线性系统,即非线性刚度k1为0,由式(22)可得系统的线性幅频响应方程
X3a2+X4=0
(24)
3 数值模拟
参照HEV-20型号激振器给以下参数赋值:ω0=300 rad/s,m=2 kg,c=0.25 N·s/m,k1=200 N/m,E0=0.05 V,εr2=7,εr1=ε0=1,S=L×b0=0.2×0.05=5×10-3m2,b0=0.05 m,d0=0.01 m。
按照式(22)、式(23)计算系统主共振幅频响应曲线并分析其稳定性。其中横坐标为调谐参数。纵坐标为振幅。
图4~图8为电磁驱动器主共振的幅频响应曲线。
图4为电磁激振器系统主共振随阻尼系数c变化的幅频响应曲线,由图4可以看出,随着调谐值的连续变化,振幅没有发生“跳跃”现象。当增大系统阻尼系数时,系统受到的阻力增大,振幅减小,共振区域变化不明显。

图4 不同阻尼的幅频响应曲线Fig.4 Amplitude frequency response curves of different damping
图5为电磁驱动器系统主共振随激励电压幅值E0变化的幅频响应曲线。由图5可知,随着调谐值的连续变化,振幅没有发生“跳跃”现象;随着电压激励电压幅值的增大,振幅和共振区域增大。
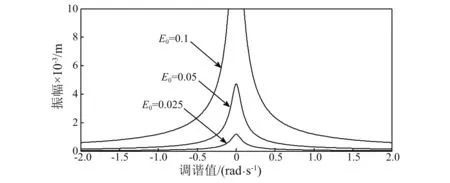
图5 不同电压值的幅频响应曲线Fig.5 Amplitude frequency response curves of different voltage values
图6为电磁驱动器系统主共振随电容两极板之间的距离d0变化的幅频响应曲线。由图6可知,随着调谐值的连续变化,振幅没有发生“跳跃”现象;随着电容两极板之间距离的增大,振幅和共振区域减小。

图6 不同极板间距离的幅频响应曲线Fig.6 Amplitude frequency response curves of different plates
图7为电磁驱动器系统主共振随电容极板长度d0变化的幅频响应曲线。由图7可知,随着调谐值的连续变化,振幅没有发生“跳跃”现象;随着电容极板长度的增大,振幅和共振区域增大。
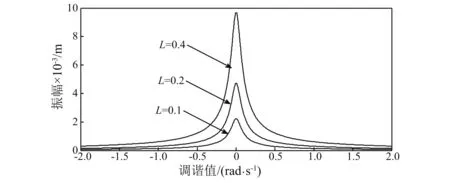
图7 不同极板长度的幅频响应曲线Fig.7 Amplitude frequency response curves of different plate lengths
图8为电磁驱动器系统关于非线性刚度k1变化的幅频响应曲线。由图8可知,当非线性刚度小于2×105时,线性系统(k1=0)与非线性系统曲线未发生明显变化,两条幅频响应曲线重合,此时可以忽略非线性项影响,用线性系统近似;但当非线性刚度大于2×106时,曲线发生“跳跃”现象,此时不可以忽略非线性项影响。
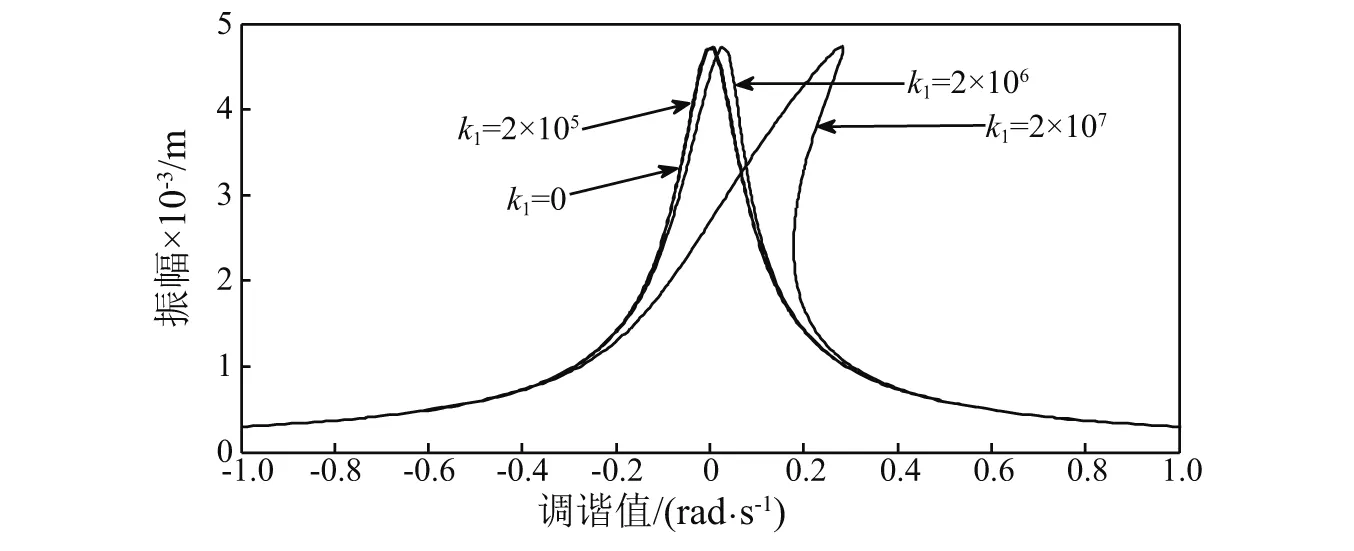
图8 不同非线性刚度的幅频响应曲线Fig.8 Amplitude frequency response curves of different nonlinear stiffness
4 结 论
新型电容式电磁驱动器电介质的直线运动,位移便于控制和测量,具有良好的实用价值。根据拉格朗日麦克斯韦方程对其建立的动力学模型,由线性项和非线性系数对比发现为弱非线性系统,与数值分析无“跳跃”现象对应。应用多尺度法分析得到了主共振的幅频响应方程,并用数值方法分析了调谐值和振幅随各参数变化的规律。结果表明: 理论分析与数值计算一致,增大阻尼可以减小系统振幅,但对共振区域影响较小;增大激励电压,系统振幅和共振区域增大;增大电容两极板间距,振幅和共振区域减小;增大电容极板长度,振幅和共振区域增大;非线性刚度小于2×105时,忽略非线性项影响,用线性系统近似,可略去稳定性分析,非线性刚度大于2×106时,不可忽略非线性项,还需分析系统的稳定性。

