混合润滑状态下粗糙界面法向接触刚度计算模型与特性研究

肖会芳， 孙韵韵， 徐金梧， 邵毅敏

(1. 北京科技大学 机械工程学院，北京 100083； 2. 西南交通大学 牵引动力国家重点实验室，成都 610031；3. 重庆大学 机械传动国家重点实验室，重庆 400044)

机械设备中广泛存在着相互接触的各类界面，例如齿轮的轮齿啮合界面、轴承的滚动体-滚道界面、机床螺栓连接界面、轧制过程的轧辊与带钢形成的轧制界面、高速列车的车轮-轨道形成的轮轨界面等[1-4]。各种类型复杂多样的接触界面的共性特征是相互接触的表面具有粗糙形貌，同时界面工作在混合润滑状态。对混合润滑粗糙界面而言，界面的法向载荷由润滑油膜和粗糙体共同承担。

接触刚度是描述界面特性最重要的参数之一，其变化直接影响界面以及机械装备系统的静态特性和动力学特性，包括接触压力分布、振动噪声响应特性、疲劳与磨损特性以及工作稳定性等[5-7]。因此，混合润滑状态下粗糙界面法向接触刚度的准确计算对机械结构与系统的性能分析与预测至关重要。

目前，关于粗糙接触界面刚度特性的研究获得了广泛的关注，研究人员基于粗糙表面形貌的统计学模型描述和分形模型描述[8-10]，并考虑界面的弹性、弹塑性或塑性变形特征，提出了不同的接触模型分析界面的法向固体接触刚度特性[11-16]。但是，这些模型均假设界面无润滑介质，没有考虑界面的混合润滑状态，获得的粗糙界面法向接触刚度模型尚不能用于混合润滑状态下粗糙界面法向接触刚度的分析与计算。

在润滑混合润滑状态界面接触刚度研究方面，田红亮等[17]考虑机床固定结合界面的表面形貌和介质层，提出各向同性虚拟材料假设的机床固定结合部动力学建模方法，将固定结合部接触面的微观接触部分假设为一种虚拟的各向同性材料，虚拟材料与固定结合部两侧的零件皆为固定连接，并通过实验验证了虚拟材料建模方法的有效性。李小彭等[18]以组合梁为研究对象，考虑界面摩擦因数，将梁结构及其结合面重构为固体-广义间隙-固体系统，将结合面等效为广义间隙，利用结合面接触刚度的分形模型与材料应变能等效的方法，获得了结合面广义间隙的材料常数，并验证结合面接触刚度分形模型的正确性。Gonzalez-Valadez等[19]采用超声反射回波测试方法，并基于界面的超声反射系数与接触刚度之间的关系，实验测试获得了混合润滑界面的接触刚度。Shi等[20]采用接触共振实验方法，测量了轻载情况下，无润滑Hertzian球接触界面和粗糙界面的接触刚度和阻尼。结果显示，粗糙界面的接触刚度远小于理论计算获得的光滑界面的刚度值。其采用实验测试的方法，进一步研究了界面存在润滑液和磨损磨粒情况下，接触界面的刚度特性。Mulvihill等[21]同时采用超声技术和数字图像相关技术(Digital Image Correlation, DIC)，测量了固体粗糙接触界面的刚度值，并对测试结果进行了对比。

上述研究通过接触界面等效建模、实验测试等方法，研究了润滑状态下粗糙接触界面的接触特性和刚度特性。但是，尚缺乏完整的混合润滑状态下界面接触刚度模型，用以表征实验测试结果。同时虚拟材料和广义间隙等效建模方法，未能实现界面固体接触刚度和液体接触刚度的分离与表征，无法获得界面的固体-液体刚度分配特性，以及界面属性参数对刚度分配特性的影响规律。

本文基于粗糙表面形貌的Greenwood-Williamson统计模型描述与界面油膜共振模型和弹簧模型，推导了界面固体接触刚度和液态介质刚度，并实现粗糙微凸体固体接触刚度与液态介质刚度的耦合，提出了一种混合润滑状态下粗糙界面法向接触刚度的计算模型，分析了接触界面形貌参数、润滑介质和接触基体材料属性对接触刚度的影响规律。由于实际机械结构的接触界面通常承受周期性载荷的加载-卸载作用，界面粗糙微凸体的塑性变形被初始的加载-卸载作用消除，稳定工况时，界面工作在弹性接触状态。例如，Gozalez-Valadez等对钢-钢接触界面的实验显示11次的加载-卸载过程可以消除界面的塑性变形。因而，本文的粗糙界面法向接触刚度计算模型，仅考虑了粗糙界面的弹性变形和弹性接触刚度。

1 混合润滑界面接触模型

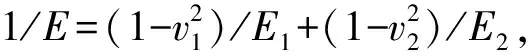
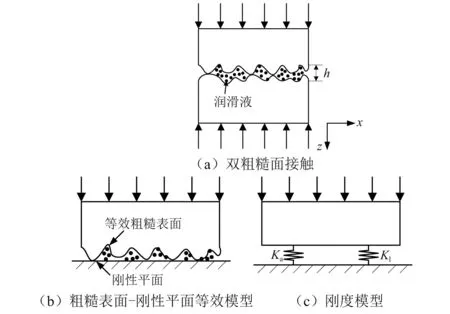
图1 混合润滑状态，粗糙界面的接触模型示意图Fig.1 Schematic of rough surface in mixed lubrication

根据混合润滑界面的载荷分配思想[22]，界面的外部法向载荷Ft由液体润滑介质压力FH和粗糙峰微凸体接触力FC共同承担，即Ft=FH+FC。 因此，界面的总刚度Kt等于固体微凸体接触刚度和液体润滑介质接触刚度之和，如图1(c)所示，即

Kt=Ka+Kl

(1)

式中:Ka为固体微凸体接触刚度；Kl为液体润滑介质接触刚度。当粗糙表面之间的距离h减小时，进入接触的固体微凸体增加，固体接触刚度在总接触刚度中的占比增加；当粗糙表面之间的距离h不断增大时，液体润滑介质厚度不断增大，界面总刚度主要由液态润滑介质刚度组成。当液体润滑介质厚度大于表面粗糙峰的峰值，接触界面完全被润滑液充满而无固体表面接触时，界面处于液压润滑状态，界面刚度完全由液体润滑介质刚度组成。

2 固体接触刚度

粗糙表面-刚性平面接触采用Greenwood-Williamson统计模型(GW模型)进行描述，如图2所示。表面粗糙体的形状为球体且各粗糙体的曲率半径均为β，粗糙微凸体的高度符合高斯分布，其高度的标准偏差为σs， 微凸体的密度为η， 各粗糙体与刚性平面的接触符合Hertzian弹性接触理论且粗糙体之间无相互作用。 单个微凸体的高度z定义为微凸体顶点与微凸体高度均线间的距离。 微凸体均线与粗糙面均线之间的距离为dd，dd=1.15σs[23]。

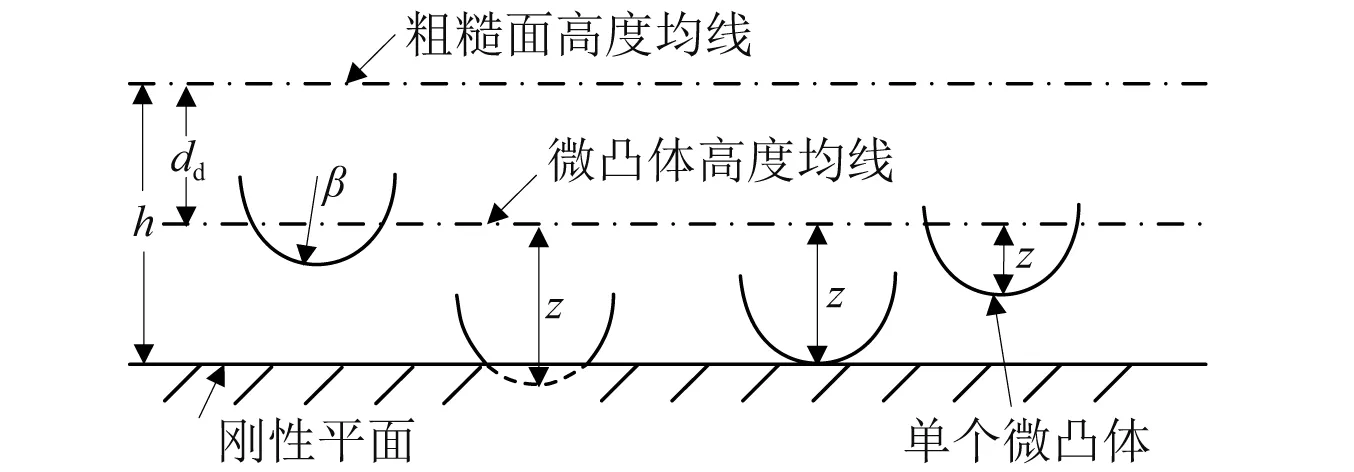
图2 粗糙表面与刚性平面的统计接触模型Fig.2 Statistical micro-contact model of the rough surface

2.1 单个微凸体接触刚度

单个微凸体与刚性平面的接触示意图，如图3所示。

图3 单个微凸体与刚性平面接触示意图Fig.3 Geometry of the single asperity contact

根据Hertzian弹性接触理论，其弹性接触力可以表示为[24]

(2)

式中:E为接触界面的等效弹性模量；w为弹性变形量，可以表示为

w=z+dd-h

(3)

接触面积可以表示为

ae(w)=πβw

(4)

单个微凸体的法向接触刚度ke定义为

(5)

即法向接触刚度可以表示为

ke(w)=2Eβ1/2w1/2

(6)

式(6)显示，单个微凸体的法向接触刚度与变形量呈非线性变化关系。

2.2 粗糙界面总刚度

采用GW统计学模型计算粗糙界面上接触微凸体的个数，并将单个微凸体接触刚度对微凸体个数进行积分，获得粗糙界面固体接触的总刚度。引入如下的无量纲参量

具有粗糙形貌的表面与刚性平面接触，当微凸体高度zn大于粗糙面均线与刚性平面之间的距离hn-dn时，微凸体与刚性平面接触，其接触概率为

(7)

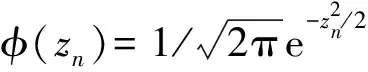
粗糙表面与刚性平面接触的微凸体的个数为微凸体总个数与接触概率的乘积，可以表示为

(8)

式中:N为粗糙表面微凸体总个数；A0为名义接触面积。粗糙表面固体接触的总载荷、接触面积和接触刚度可以分别表示为

(9)

(10)

(11)

将式(2)，式(4)，式(6)，式(8)分别代入式(9)～式(11)，则粗糙界面固体接触的总载荷、接触面积和接触刚度可以分别表示为

(12)

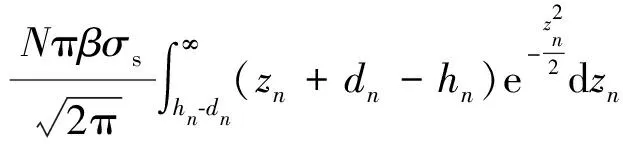
(13)

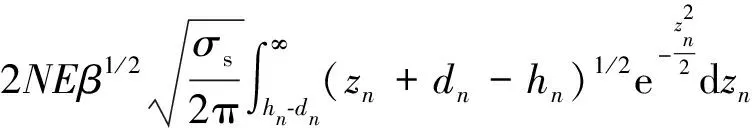
(14)

3 混合润滑界面接触刚度

3.1 液体介质接触刚度

图1所示的接触基体-润滑介质-接触基体的等效液体刚度模型，如图4所示。液体润滑层的厚度h为两粗糙面均线之间的距离。由于接触基体与液体润滑层的声阻抗之间存在明显的差异，入射超声波在固-液界面发生反射与透射，利用超声波反射系数与液体润滑层厚度和刚度之间的关系特性，可以确定液体润滑层的接触刚度。

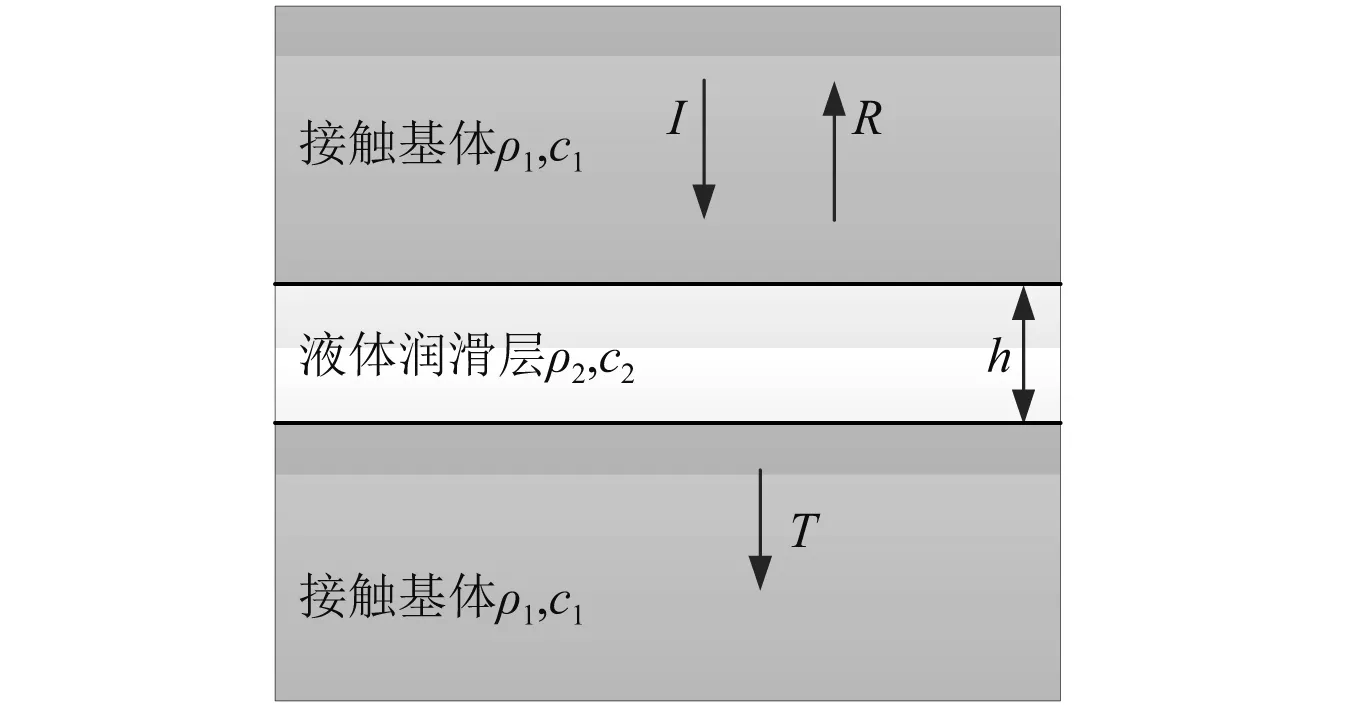
图4 超声波在接触基体-润滑介质-接触基体模型传递示意图Fig.4 Schematic of the transmission of ultrasonic in the contact body-lubricant-contact body model

根据液体界面油膜共振模型，固-液接触界面的超声反射系数可以表示为[25]

(15)

式中:λ0为超声波在润滑液体中的波长；Z1和Z2分别为固体和润滑液体的声阻抗， 可以表示为Z1=ρ1c1,Z2=ρ2c2，ρ1和c1分别为固体的密度和超声波的波速，ρ2和c2分别为润滑液体的密度和超声波的波速。

根据液体界面的弹簧模型，当液体中的声波波长λ2远大于液体油膜层厚度h时，整个液体润滑层可看作整体的反射体，界面的超声反射系数可以表示为[26]

(16)

式中:kl为单位面积上的液体润滑层接触刚度；f为超声波的频率。

联立式(15)和式(16)，单位面积上的液体润滑层接触刚度可以表示为

(17)

由于液体界面的弹簧模型仅适用于声波波长λ2远大于流体层厚度h的情况，即λ2≫h，则有

(18)

采用泰勒级数将sin(2πh/λ2)沿2πh/λ2=0展开，并考虑界面的名义接触面积，则液体润滑介质接触刚度可以近似表示为

(19)

式(19)显示液体接触刚度由润滑介质厚度、液体属性、接触固体属性和接触面积共同决定，而与入射超声波的频率无关，因此不会受到实验测量中超声衰减引起测量能力降低的限制。

3.2 界面法向总刚度

联立式(1)，式(14)和式(19)，混合润滑粗糙界面的总刚度可以表示为

(20)

式(20)显示，混合润滑粗糙界面的接触刚度与界面材料属性、表面粗糙形貌、接触基体和润滑介质的声阻抗等因素相关。同时，界面的固体接触刚度与液体接触刚度相互耦合，液体接触刚度与界面的表面粗糙形貌相关，而固体接触刚度也与液体润滑层的厚度相关。

4 模型有效性验证

4.1 与已有的刚度实验结果对比

为了验证本文刚度计算模型的正确性，将模型计算获得的刚度值和实验测量获得的润滑粗糙界面的刚度值进行对比。Gonzales-Valadez等采用超声反射系数法测量了钢-油-钢、钢-水-钢润滑界面的接触刚度值。界面的等效材料参数为E=115 GPa,ν=0.3, 名义接触面积A0=25×10-6m2。测试钢样的表面粗糙度值分别为Ra=4.84 μm和Ra=4.94 μm, 对应的微凸体高度标准偏差σs=3.63 μm和σs=3.71 μm。实验测试所用的不同材料的属性参数，如表1所示。采用本文固体接触刚度模型式(14)和液体介质接触刚度模型式(19)计算获得的法向接触刚度-载荷变化关系曲线与实验测量获得的数据对比图，如图5所示。图5显示，模型的计算结果与实验测试结果基本一致，说明本文的混合润滑界面接触刚度的模型是有效的、可靠的。

图5 混合润滑界面接触刚度的模型计算结果与实验结果对比Fig.5 Comparison of the interface contact stiffness versus pressure between the model results and experimental results for different lubrication

表1 实验测试采用的不同材料的属性参数Tab.1 Parameters of different materials used in experimental tests

4.2 实验测试

为了进一步验证本文刚度计算模型的正确性，设计了螺栓连接界面实验装置，进行冲击激励下的幅频响应测试，将实验测试获得的系统固有频率和代入本文模型计算刚度值获得的系统固有频率进行对比。实验装置，如图6所示。实验采用自由悬挂锤击法测试，利用力锤敲击上表面产生冲击激励，在钢板下表面安装加速度传感器PCB 352C33，测量界面无润滑和界面存在润滑油时的法向加速度响应。

图6 实验装置Fig.6 Experimental setup

螺栓连接界面由两块材料为45#钢、尺寸为300 mm×50 mm×8 mm的钢板，通过14个M6螺栓连接形成。每个螺栓的拧紧力矩为8 N·m，即每个螺栓的预紧力为10 kN，界面的平均压力为p=9.4 MPa，名义接触面积A0=1.5×10-2m-2。采用激光共聚焦显微镜LEXT对相互接触的两钢板表面进行表面形貌测试，采样间隔为0.625 μm。获得的钢板表面形貌，如图7所示。计算获得的表面形貌参数分别为Ra=1.4 μm，η=0.63×1011m-2，β=0.64 μm。将表面形貌参数σs,η和β，等效弹性模量E=115.4 GPa代入式(14)，获得粗糙界面固体接触刚度Ka=1.082×1011N/m。

首先进行无润滑螺栓连接界面的实验测试，获得界面系统的幅频特性曲线。其次，在接触界面加入少量的润滑油GST PREMIUM 32，润滑油的属性参数为ρ=863 kg/m3，c=1 530 m/s，代入界面法向总刚度模型式(20)计算获得界面的总刚度Kt=1.8×1012N/m，测试混合润滑界面在冲击激励作用下的加速度响应，获得界面系统幅频特性曲线。无润滑界面系统和有润滑界面系统的幅频特性曲线，如图8所示。图8显示，与无润滑粗糙界面相比，润滑粗糙界面的固有频率增大，表明界面的刚度值增加。

图7 实验样品表面形貌Fig.7 Surface topograph of test specimen

图8 螺栓连接界面法向幅频响应曲线Fig.8 The frequency response in normal direction

采用有限元仿真计算方法对螺栓连接界面系统进行模态分析，获得系统的固有频率。螺栓连接界面的有限元分析模型，如图9所示。钢板采用SOLID185单元离散，两钢板的接触特性采用自定义刚度单元MATRIX27表征，单元MATRIX27的输入值为刚度模型获得的法向刚度Ka=1.082×1011N/m和Kt=1.8×1012N/m，对应于无润滑界面和有润滑界面的法向刚度，切向刚度值为法向刚度的0.8倍[27]。实验测试获得的前4阶固有频率与有限元计算获得的固有频率的对比值，如表2所示。表2显示，实验测试获得的固有频率与采用本文刚度模型计算获得的固有频率相对误差小于7%，说明本文的界面固体接触刚度的模型是有效的。

图9 有限元计算模型Fig.9 The finite element analysis model

表2 实验固有频率与仿真计算获得的固有频率对比Tab.2 Comparison between the natural frequencies from experimental test and FEA

5 计算结果与分析

改变界面的接触特性参数，包括微凸体高度的标准偏差σs、润滑液类型和接触体材料属性，获得不同界面特性参数时固体接触刚度、液体接触刚度和刚度分配比率随界面间距离的变化关系曲线。计算采用的参数值，如表3所示。

表3 计算参数值Tab.3 Calculation parameters

5.1 接触刚度-界面距离关系曲线

5.1.1 不同界面粗糙形貌

不同界面粗糙形貌时，界面的固体接触刚度、液体介质接触刚度和总刚度随界面间距离hn的变化关系曲线，如图10所示。微凸体高度的标准偏差分别为σs=0.05 μm, 0.5 μm, 3 μm，表征光滑界面、中等粗糙界面和粗糙界面。

当界面处于混合润滑状态时，界面间无量纲距离的变化范围通常在hn=[0.5,3][28]。图10(a)显示，对光滑界面，固体接触刚度Ka远小于液体介质接触刚度Kl，界面的接触总刚度几乎完全来自于液体介质接触刚度。随着界面粗糙度增加，固体接触刚度逐渐增大，同时液体介质接触刚度逐渐减小。对粗糙界面，如图10(c)所示，液体介质接触刚度远小于固体接触刚度，界面的总刚度几乎完全来自于固体接触刚度。这是由于当界面粗糙度很小时，界面几乎被润滑液充满，粗糙微凸体的接触很少，因而固体接触刚度很小，液体介质接触刚度较大；随着粗糙度增大，固体微凸体的接触增多，相应的液体介质接触减少，因而固体接触刚度增大，液体介质接触刚度减小；对粗糙界面，液体介质仅存在于粗糙微凸体之间的空隙，随着界面距离变化，固体接触刚度会剧烈增大，而液体介质接触刚度变化很小。

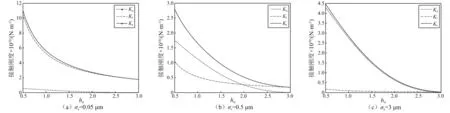
图10 不同界面粗糙形貌时的接触刚度-界面距离关系曲线Fig.10 Plots of contact stiffness versus non-dimensional separation for surfaces with different roughness

图5所示的实验结果显示，液体介质的接触刚度几乎不随载荷变化，这是由于实验测试样品的表面粗糙度较大(σs=3.63 μm和σs=3.71 μm)，引起固体接触刚度随载荷增大而增大，而液体介质的接触刚度几乎不变。图10同时显示，界面的固体接触刚度、液体接触刚度和总刚度均随着界面间距离减小呈非线性递增。

5.1.2 不同润滑介质

不同界面润滑介质时，界面的固体接触刚度、液体介质接触刚度和总刚度随界面间距离hn的变化关系曲线，如图11所示。其中，图11(a)对应的介质为水，图11(b)对应的介质为空气。不同介质的属性参数，如表4所示。界面的粗糙度值为σs=0.5 μm。图11显示，当润滑介质变化时，界面的液体介质接触刚度和总刚度发生明显变化。与图10(b)的润滑油介质相比，当介质变为水后，润滑介质的声阻抗变大(如表4所示)，因此液体介质接触刚度减小，而固体接触刚度几乎无变化，因而总刚度也相应减小。当介质变为空气时，界面等效于无液体介质，介质的接触刚度非常小，界面总刚度等于固体接触刚度。

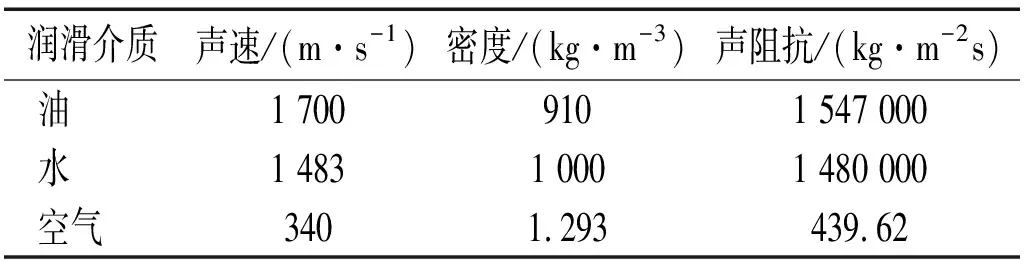
表4 不同润滑介质的属性参数Tab.4 Property parameters of different lubricants

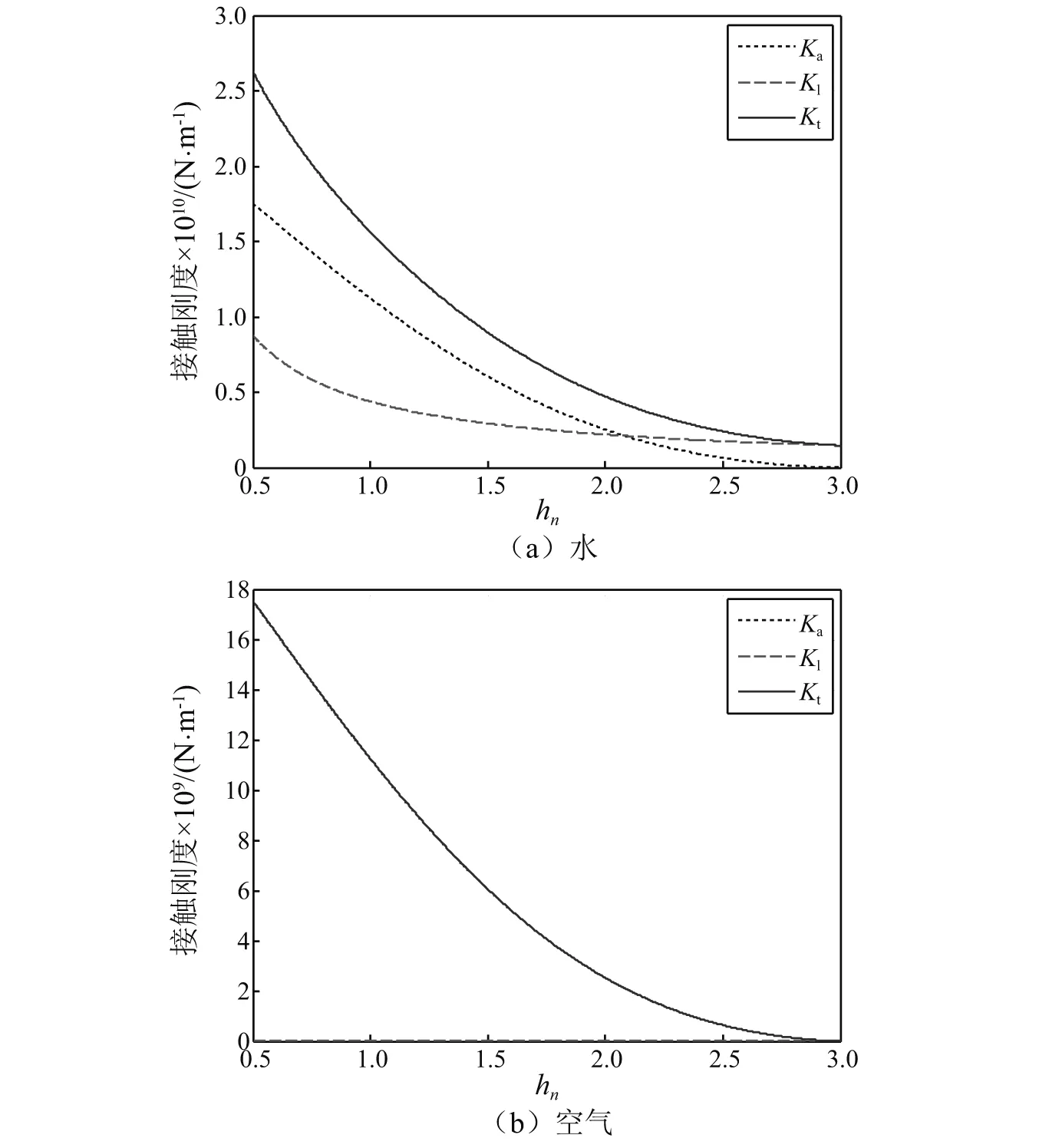
图11 不同润滑介质时，界面的接触刚度-距离关系曲线Fig.11 Plots of contact stiffness versus non-dimensional separation for different lubricant

5.1.3 不同接触基体材料

不同接触基体时，界面的固体接触刚度、液体介质接触刚度和总刚度随界面间距离hn的变化关系曲线，如图12所示。其中，图12(a)对应的基体材料为铸铁，图12(b)对应的基体材料为铝。不同基体的材料与声学属性参数，如表5所示。界面间润滑介质为润滑油，界面的粗糙度值为σs=0.5 μm。与图10(b)的钢基体相比，基体为铸铁和铝时，材料的弹性模量递减，其接触总刚度依次递减，铸铁基体次之，铝基体最小。接触基体材料不同时，液体接触刚度差异较小，但是固体接触刚度差异较大，导致总刚度之间的差异。

表5 不同接触基体的材料与声学属性参数Tab.5 Material and sound parameters of different contact bodies

图12 不同基体界面的接触刚度-距离关系曲线Fig.12 Plots of contact stiffness versus non-dimensional separation for surfaces with different materials

5.2 刚度分配特性

不同界面粗糙形貌时，界面的固体刚度分配比率和液体刚度分配比率随界面间距离hn的变化关系曲线，如图13所示。图13显示，对光滑界面，固体接触刚度占总刚度比值的最大值仅为0.07。随着表面粗糙度增加，固体接触刚度占总刚度的比率不断增加，而液体接触刚度占总刚度的比率不断减小。对粗糙界面，固体接触刚度占总刚度比值的最大值达到0.97。当界面间距离hn>3时，即hn大于标准高斯概率密度函数的最大微凸体高度时，界面的总刚度等于液体接触刚度，界面处于液压润滑状态。

不同润滑介质时，界面的固体刚度分配比率和液体刚度分配比率随界面间距离hn的变化关系曲线，如图14所示。图14显示，与润滑介质为油时相比，润滑介质为水时的固体接触刚度所占比率增加，对应的液体接触刚度所占比率减小。当润滑介质为空气时，固体接触刚度占总刚度的比率为1，接触总刚度完全来自于固体接触刚度。

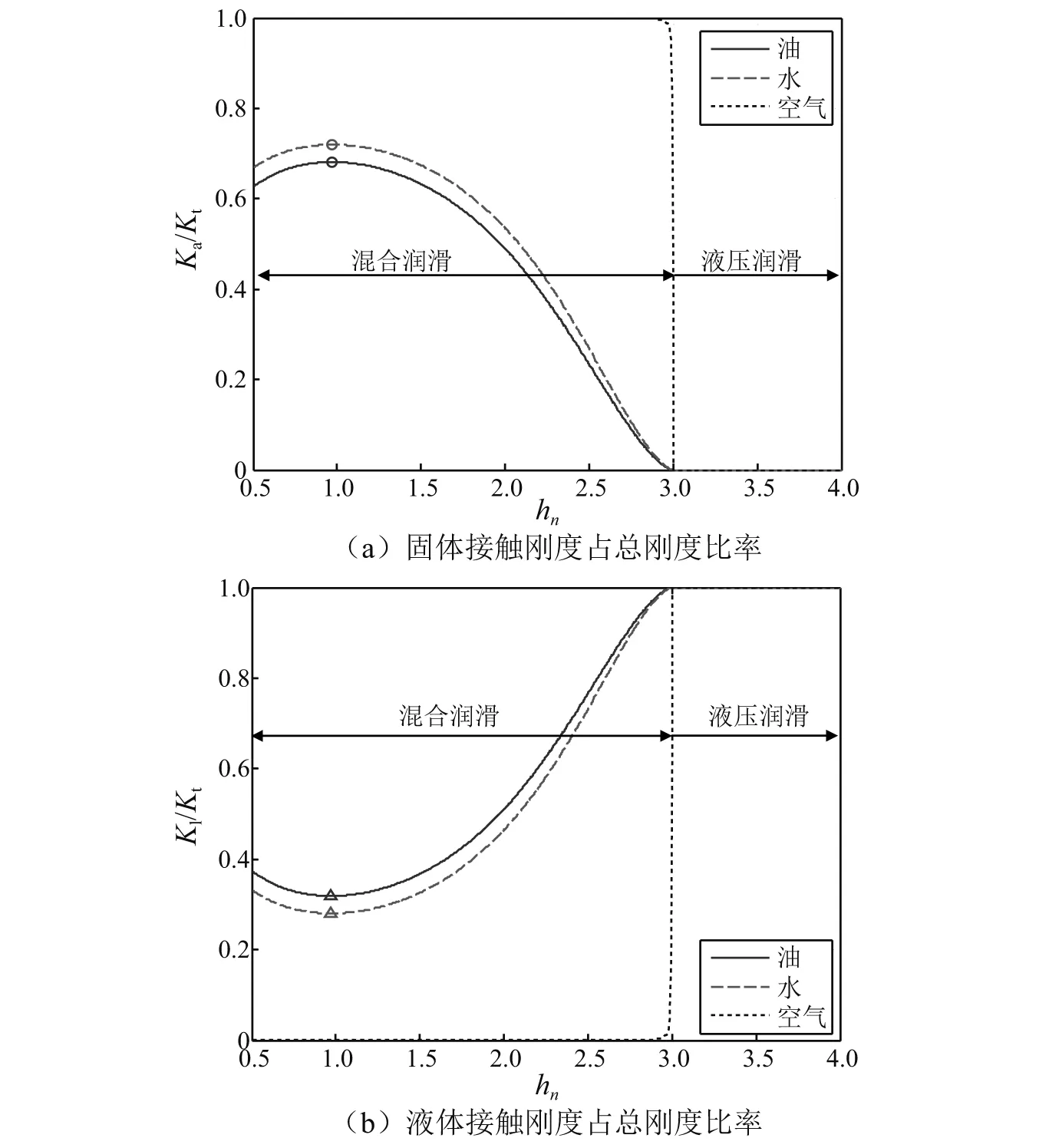
图14 不同润滑介质时，界面的接触刚度分配比率Fig.14 Plots of contact stiffness ratio for interface with different lubricants

不同的接触基体材料时，界面的固体刚度分配比率和液体刚度分配比率随界面间距离hn的变化关系曲线，如图15所示。图15显示，接触基体为铝时，固体接触刚度占总刚度的比值最小，其最大的固体刚度比率为0.425；接触基体为钢时，固体接触刚度占总刚度的比值最大，其最大固体刚度比率为0.681。液体接触刚度的比率与固体接触刚度比率的变化趋势相反，铝基体最大，而钢基体最小。

图13，图14和图15同时显示，表面形貌对界面接触刚度的分配影响最大，接触基体材料次之，影响较小的是液体润滑介质。对不同的表面粗糙度界面、不同润滑介质界面、不同接触基体界面，固体接触刚度占总刚度的比值随界面间距离均呈先增大后减小的变化趋势，存在最大值，且最大值对应的无量纲界面间距离hn=1，相应的液体接触刚度的比率最小，即界面间距离等于粗糙界面微凸体高度标准偏差时，固体接触刚度占总刚度的比值最大。

图15 不同基体材料时，界面的接触刚度分配比率Fig.15 Plots of contact stiffness ratio for surfaces with different material

6 结 论

(1) 本文提出了一种混合润滑状态下粗糙界面法向接触刚度的计算方法，并通过与实验测试结果对比验证了计算模型的正确性。

(2) 接触基体材料的表面形貌和弹性模量是影响固体接触刚度的主要因素。随着界面粗糙度增加，固体接触刚度逐渐增大，同时液体接触刚度逐渐减小；弹性模量增加时，界面固体接触刚度增大，但液体接触刚度差异较小，导致总刚度之间的差异。

(3) 润滑介质的声阻抗是影响液体接触刚度的主要因素，声阻抗增大时，液体接触刚度减小，但固体接触刚度变化很小，导致总刚度也相应减小。

(4) 随着表面粗糙度增加、接触基体弹性模量增加、润滑介质声阻抗减小，固体接触刚度占总刚度的比率增加，而液体接触刚度占总刚度的比率减小；当界面间无量纲距离hn>3时，界面的总刚度等于液体接触刚度，界面处于液压润滑状态。

(5) 表面形貌对界面接触刚度的分配比率影响最大，接触基体材料次之，影响较小的是液体润滑介质。