钙质砂动态力学特性试验研究

魏久淇， 王明洋， 邱艳宇， 赵章泳

(1. 陆军工程大学 防灾减灾爆炸冲击国家重点实验室，南京 210007；2. 军事科学院 国防工程研究院，河南 洛阳 471023；3.河南省特种防护材料重点实验室，河南 洛阳 471023)

钙质砂作为一种海洋生物成因的岩土介质，主要成份为CaCO3,广泛分布于北纬30°和南纬30°之间热带海洋地区，其生成机制的特殊性，形成了压缩性高，孔隙比大，内摩擦角大，颗粒易破碎等特性[1-5]。近年来，我国“一带一路”愿景的达成，海上丝绸之路途径地区多为钙质砂分布区，南海诸岛和海外基地建设及维护的需求越来越大。岛礁建设和维护都避不开深厚的原状或吹填的钙质砂地基，同时，中国面临海上一场信息条件下的局部战争的风险有增无减，南海诸岛及海外基地港口的前哨作用越来越大。岛礁上钙质砂，不仅自身常受到风、浪等周期荷载的作用，而且可能还承受飞机降落、爆炸冲击等强荷载的作用。因此研究钙质砂的动态力学特性显得尤为重要。

分离式霍普金森压杆(Split Hopkinson Pressure Bar, SHPB)常用于研究材料在中高应变率(101～104s-1)下的动态力学特性。目前，诸多学者利用该装置研究了应变率、含水率、初始密度、颗粒级配、侧限条件对石英砂动态力学特性的影响[6-15]。研究表明：应变相同时，初始密度越大，砂的承载力越大；侧限条件提供的刚性约束越强，砂越难形变；级配越好，砂的承载力越大；含水率对石英砂的动力响应特性也有影响。然而学者对石英砂应变率效应的认识存在较大争议，Bragov等[16-20]认为石英砂有明显的应变率效应，而Song等认为石英砂基本没有应变率效应，对此问题认识不统一的可能原因：砂土材料孔隙率大，密度低，波速小，与压杆的波阻抗相差大，较难满足砂样应力均匀性。前人为了满足该基本条件，试样尺寸很小，每次装样为几克，砂土颗粒材料本身均匀性差，装样再如此少，试验数据的离散性可能会比较大。且前人大多展示平均后的试验数据，同工况下各组试验结果未有展示，因此试验结果的重合度值得怀疑，故试验结果的偶然性大。钙质砂作为一种海洋生物成因的岩土介质，其工程力学性质与普通的石英砂有显著的差别。我国对钙质砂的研究始于20世纪70年代，至今已取得丰硕成果，但研究成果主要集中钙质砂的物理基本性质、颗粒破碎及静力压缩等特性[21-23]。虞海珍等[24]研究了钙质砂的液化特性，徐学勇等[25]研究了饱和钙质砂在爆炸应力波作用下的动力响应特性。Farr利用自行研究的单轴加载装置研究了埃尼威托克海滩环礁附近钙质砂在应变率0.01～2 000 s-1内的力学特性，研究表明钙质砂在应变率0.01～1 000 s-1内有明显的应变率效应，在1 000～2 000 s-1内不明显，但鉴于当时技术水平有限性，研究结果也未展示同工况下重合度，因此试验结果仅具参考意义。综上可知，前人对石英砂动态力学特性研究已经比较深入，但石英砂是否具有应变率效应还存在争议，对钙质砂动态力学特性研究更是比较鲜见。

本文利用改进的SHPB试验装置，研究了钙质砂在应变率500 s-1，900 s-1，1 200 s-1及1 400 s-1下和初始密度为1.18 g/cm3，1.24 g/cm3，1.29 g/cm3，1.36 g/cm3及1.38 g/cm3动力响应，并做了相应部分石英砂的对比试验。根据试验结果，拟合出了钙质砂的p-(ρ/ρ0)方程，并得到了钙质砂在一维应变条件下的p-εv方程。

1 试验内容与方法

1.1 试验设备与原理

如图1所示，SHPB设备主要由子弹、入射杆和透射杆等其他测量设备和辅助设备组成。试验时由气体驱动的子弹从枪筒内射出，子弹以一定的速度撞击入射杆并在杆内产生弹性应力波，当应力波到达试样前端面时，因试样和杆的波阻抗不匹配，一部分入射波将反射回入射杆(反射波)，另一部分则将透过试样传递到透射杆中(透射波)，并由阻尼器吸收。应变时程曲线通过粘贴在入射杆和透射杆上的半导体应变片测得，灵敏系数约为110.00。材料的动态应力、应变和应变率分别按以下公式计算。

(1)

(2)

(3)

图1 分离式霍普金森压杆Fig.1 Schematic of split Hopkinson pressure bar

本文所用SHPB试验装置为直径37 mm的铝杆。子弹长度、入射杆以及透射杆分别为400 mm，2 000 mm和2 000 mm。套筒材质为4340钢，弹性模量为210 GPa,泊松比为0.3，内径37.1 mm，外径为47 mm，长为94 mm；垫块材质跟压杆材质完全相同，直径为37 mm，厚度为30 mm。入射杆前端面贴有橡胶材质的整形器，砂样装样流程参考Song等的研究成果。

1.2 试验方案的可行性分析

由于本文对SHPB试验装置进行了改进，需考虑增加的铝垫块和套筒对试验结果造成的影响。图2为改进的SHPB经调平后的空打波形图。由图2可知，入射波与透射波基本一致，套筒信号基本为0，这一方面说明套筒和垫块对试验结果影响较小，另一方面说明垫块与压杆因撞击而产生的横向应变对套筒应变信号的采集基本没有影响。

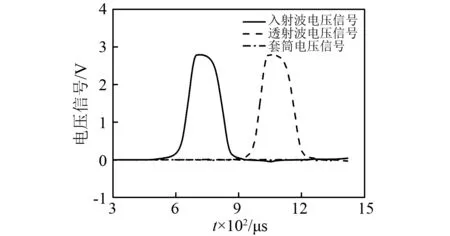
图2 空打波形图Fig.2 Without sample waveforms

由图1可知，本文在套筒外表面中间沿环向贴有半桥半导体应变片，主要是为了得到砂样体应力-应变曲线。每次试验在套筒内壁涂抹适量的润滑油以减小砂样与套筒内壁的摩擦力，图3为砂样受冲击应力均匀时套筒的受力示意图。

图3 套筒受力分析Fig.3 Sleeve force model

由图3可知，若套筒与砂样等长，则套筒内壁受均布径向力，套筒受力模型可以看成平面应力问题，则砂的应力和应变可由以下公式计算

σrr=σθθ=0.5(a2-1)Ecεc

(4)

εrr=εθθ=0.5εc[(1-vc)+(1-vc)a2]

(5)

式中：σrr，σθθ分别为极坐标下径向应力和环向应力；εrr，εθθ为极坐标下的应变；Ec，vc分别为套筒的弹性模量和泊松比；εc为应变片测到的套筒环向应变；a为套筒的外径与内径的比。

套筒内部及砂样的应力场和变形场很难通过简单的测量技术获得，现在主要的手段是通过测量套筒外表面环向应变，然后运用式(4)和式(5)反推出砂样的应力和应变场。文献[26]在推导式(4)和式(5)的过程中，认为套筒处于平面应力状态，这一假设忽略了砂样端部对套筒受力状态的影响。当砂样长度Ls与套筒长度D之比较大时，端部效应影响范围较短，套筒中间一段区域可认为处于平面应力状态，此时式(4)和式(5)得到应力和应变场与真实值相差不大；反之，当砂样长度Ls与套筒长度D之比较小时，端部效应影响范围较长，套筒则不能认为处于平面应力状态，此时应力和应变场的理论值与真实值之间相差很大，式(4)和式(5)失效。国内外许多学者在分析其试验数据时，大都直接采用了Ravi-Chandar等的理论计算方法，并未考虑端部效应的影响，这就导致其结果的准确性受到质疑，尤其是试样长度较短的大直径试验结果。

本文套筒在整个过程中都处于弹性阶段，经过与大量的有限元模拟结果对比发现，理论值与真实值之间存在一定的比例关系，定义比例系数k为真实值(有限元模拟结果)与理论值之比。研究发现，比例系数k与砂样套筒长度比Ls/D，套筒内外经之比rin/rout，套筒模量与砂样模量之比等因素有关。由于本问题的重要性和普遍性及相应的计算量巨大，作者决定对这一问题进行深入研究，单独撰文独立发表。经过与有限元模拟结果对比，本文的比例系数k值取1.65。故砂的体应力与体应变为

p=1/3(σzz+2kσrr)

(6)

εv=εzz+2εrr≈εzz

(7)

式中：p为体应力；εv为体应变；本文εrr非常小，约为10-4量级，εzz为10-1量级，因此εrr可以忽略，故砂样受冲击荷载压缩可以看成一维应变问题。

1.3 砂 样

本文所用钙质砂取自我国南海某珊瑚岛礁附近，石英砂为我国标准砂福建砂。图4(a)和图4(b)分别为钙质砂和石英砂试样。钙质砂颗粒骨架密度约为2.82 g/cm3，主要成分为CaCO3；石英砂颗粒骨架密度约为2.63 g/cm3，主要成为SiO2。本文将砂样中大于1.18 mm和小于0.15 mm和的粒径剔除，图5为试样级配曲线和原始砂样级配曲线，试验工况归纳于表1。

图4 试验砂样图 Fig.4 Sand specimens tested

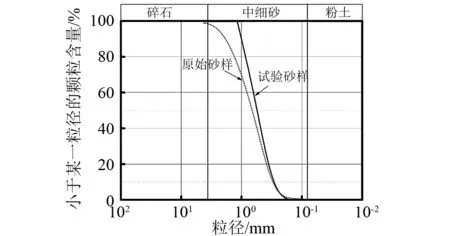
图5 砂样颗粒级配曲线Fig.5 Grain size distribution

2 试验结果与分析

本文在入射杆前段粘贴有直径为10 mm厚度约为1 mm橡胶片，主要为了延长上升沿时间以使砂样前后界面应力平衡，图6(a)为本文试验时的典型波形。SHPB试验时试样前后端面应力平衡是评判数据有效的重要方方法。受文章篇幅所限，本文将密度最小密度砂样应力平衡结果表示于图6(b)，由图6(b)可知试样前后端面基本满足应力平衡条件，因此本文试验结果有效，砂土密度越大，越易达到应力平衡。

表1 试验工况表Tab.1 Summary of SHPB tests

2.1 应变率效应

为了证明本文同工况下数据重合度高，更好地说明应变率效应问题，将钙质砂和石英砂不同应变率所有工况下的轴向应力-应变曲线分别表示于图7(a)和图7(b)。由图7(a)和表1可知，装样控制精度高，同工况下应力-曲线重合度高，钙质砂在应变率500～1 400 s-1内基本没有应变率效应。由图7(b)和表1可知，编号S60-0.15-29石英砂应力-应变曲线异常，这主要是因为该试样装样时误差大造成的，石英砂在应变率425～760 s-1内也基本没有应变率效应。对比图7(a)和图7(b)可知，在相同气压驱动子弹撞击引起的荷载作用下，石英砂的轴向变形远小于钙质砂，应变相同时石英砂的应力远大钙质砂，因此密实度相同，石英砂的承载力远大于钙质砂。

(a) 试验原始波形

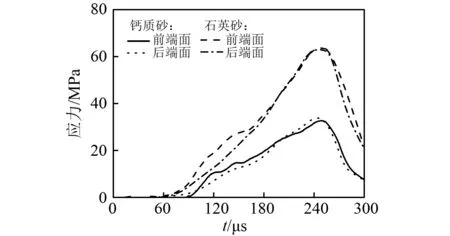
(b)砂样动态应力平衡图6 试验结果可靠性分析Fig.6 Reliability analysis of test results

(a)钙质砂

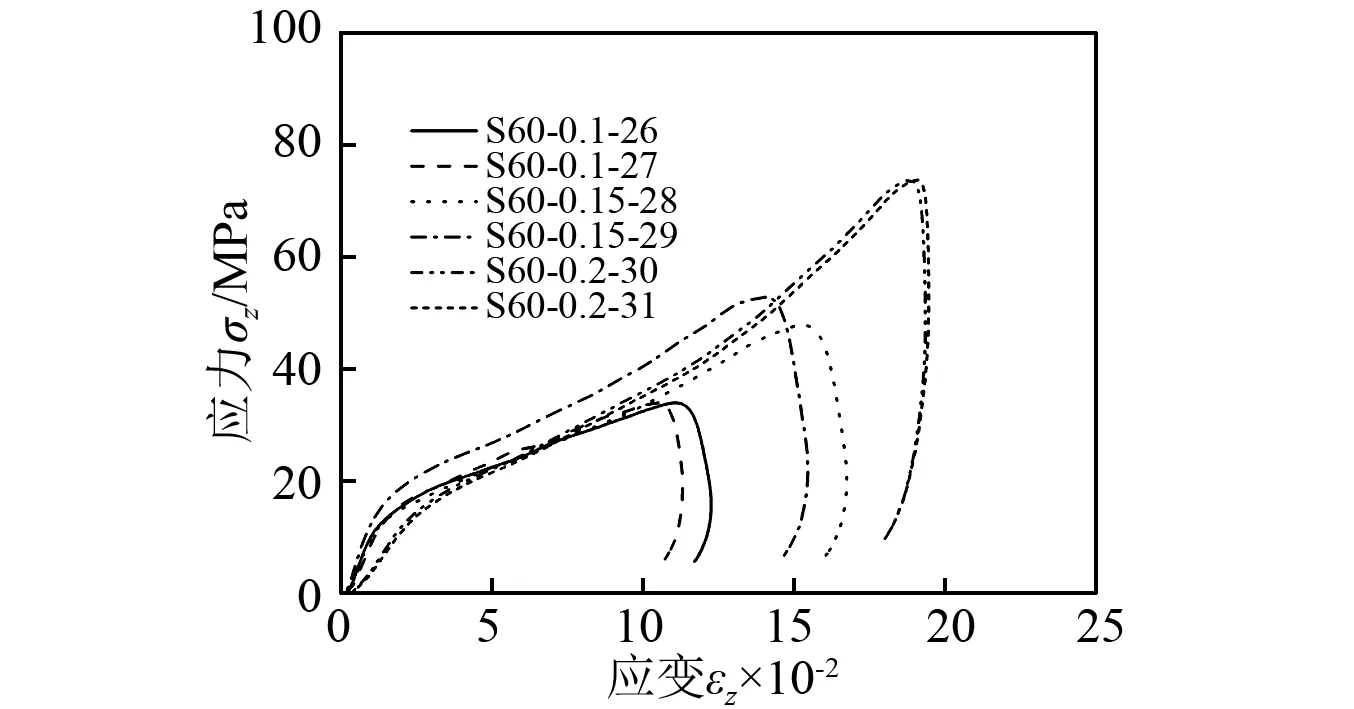
(b)石英砂图7 不同应变率下砂的应力-应变曲线Fig.7 Stress-strain curves of sand under different strain rates

2.2 密度的影响

图8(a)和图8(b)分别为初始密度不同的钙质砂与石英砂的体应力-应变曲线。每条曲线为同工况下的平均值，并插以误差棒来表示该工况下的误差。由图可知砂应变相同时，初始密度越大，应力越大，石英砂所做结果与Lou等研究结果规律一致。

(a)钙质砂

(b) 石英砂图8 初始密度对体应力-应变曲线的影响Fig.8 Influence of initial density on stress-strain curves of body

在图8(a)和图8(b)分别取三条等值线，从左至右依次交于1～5点，各点所对应的砂的密度汇总于表2。由表2可知，初始密度不同的钙质砂，应力p相同时，各点密度基本相等，石英砂因试验组数较少，各点密度稍显离散。因此钙质砂在冲击荷载作用下，砂的应力p与密度ρ有一一对应关系。

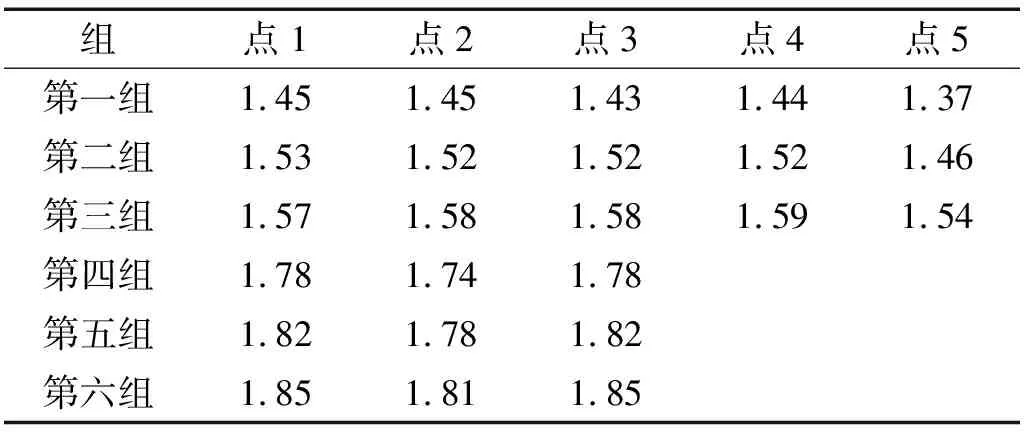
表2 各点密度汇总表Tab.2 Summary of density of points g/cm3

2.3 物态方程

本文用Murnaghan提出的式(8)来拟合钙质砂的物态方程[27]

p=k0/k[(ρ/ρ0)k-1]

(8)

式中：k0，k分别为初始体积模量和它对压力的一阶倒数。将拟合曲线和试验曲线表示于图9(a)，拟合得出钙质砂的k=4.457，标准差为0.023；k0=26.737，标准差为0.064；拟合方程相关系数为97.507%，因此钙质砂在较低冲击荷载下物态方程为

p=5.998[(ρ/ρ0)4.457-1]

(9)

式中：ρ0=1.18 g/cm3，一维应变条件时

ρ/ρ0=1/(1-εv)

(10)

则式(9)可以化成

p=k0/k[(1-εv)-k-1]

(11)

故钙质砂一维应变条件下的p-εv方程为

p=5.998[(1-εv)-4.457-1]

(12)

将p-εv方程曲线和试验曲线表示于图9(b)，由图9(b)可知方程曲线跟试验曲线重合度较高。

(a)p-(ρ/ρ0)曲线

(b)p-εv曲线图9 试验曲线和拟合曲线Fig.9 Test curve and fitting curve

3 结 论

本文利用改进的直径为37 mm铝制SHPB装置，研究了应变率和密度对两种砂动态力学特性的影响，主要得出以下结论：

(1) 钙质砂在应变率500～1 400 s-1内基本没有应变率效应，石英砂在应变率425～760 s-1内也基本没有应变率效应。

(2) 应变相同时，试样初始密度越大应力越高；密实度相同时，钙质砂的承载力远小于石英砂。

(3) 在冲击荷载作用下，两种砂的应力p跟密度ρ有一一对应关系。

(4) 拟合出了钙质砂的p-(ρ/ρ0)物态方程，得到了钙质砂在一维应变条件下的p-εv方程。