我国生产要素配置效率的测算

王建斌

（1.南京林业大学 经济管理学院，南京 210037；2.上海财经大学 经济学院，上海 200433）

0 引言

全要素生产率是经济增长率中去除劳动、资本等生产要素数量增长贡献后的差值，反映了经济发展中技术进步、生产要素配置效率的改善以及生产的规模收益。相比于GDP增长率，全要素生产率的波动更能反映经济增长的质量以及增长的可持续性。我国经济进入了新常态，经济增长率出现下降，原有依靠投资促进资本积累推动经济发展模式受到质疑，通过改善生产要素配置效率，推动技术进步,依靠全要素生产率上升促进经济增长成为学术界和决策层的共识。当前学术界主要采用3种方法对全要素生产率进行分析，分别为索罗残差估计法，数据包络分析（DEA）和SFA（随机边界分析）。其中最经常用的是随机边界分析法。随机边界分析将生产函数的形式设定为超越对数生产函数，这种函数形式放松了规模报酬不变和技术中性的假定，并允许劳动力和资本非充分利用，比传统的科布道格拉斯函数更灵活，便于全要素生产率的分解。因此，本文采用随机边界分析法分析要素价格对配置效率的影响。要素的投入成本是由要素投入量与价格决定的，因此相对价格是要素配置效率的主要影响因素，从要素价格出发研究要素配置效率给全要素生产率带来的影响的途径是合理的。本文建立的“要素价格—要素配置效率—TFP”的分析逻辑有较强的政策含义，更能促进TFP研究与宏观经济政策的对接。

基于国内外学者的相关研究成果，本文通过构建随机边界模型对区域生产要素配置进行研究，探讨要素价格波动对要素配置效率的影响。并将传统增长核算中的劳动要素分为普通劳动和人力资本两种劳动要素，重点分析了普通劳动力、人力和物质资本三个因素的配置效率及其对TFP变化的影响。

1 随机边界模型的构建

本文基于超越对数生产函数，建立以下随机边界模型：

其中：

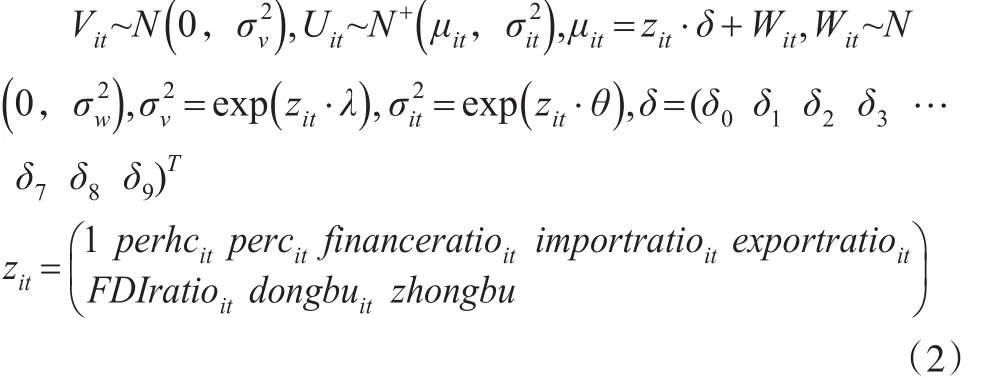
其中，Lit指第i省第t期从业人员的资本存量，Kit指不同年份的资本存量，Perhcit指第i省第t期的人力资本存量，percit指第i省第t期的人均资本存量，financeratioit指第i省第t期的财政支出量，importratioit指第i省第t期的进口贸易额，出口贸易额用exportratioit来表示，外商投资占区域生产总值的比例用FDIratioit来表示，东部区域的虚拟变量用dongbuit来表示，zhongbu指中部区域的虚拟变量，Vit指第i省第t期生产过程的随机误差项，Uit指第i省第t期的技术无效率项。

参考kumbhakar等（2016），通过引入要素价格信息，本文将全要素生产增长率分解为前沿技术进步速度、技术效率、规模经济和配置效率这四个部分。

公式（3）中，用FTP表示前沿技术进步率，TEit代表i省在第t期时候的技术变化率代表要素配置的变化率代表生产规模经济的变化代表产出弹性，Sijt代表要素成本额。代表规模弹性的大小。

根据以上对数函数的随机边界模型，可以推导出各区域要素配置效率的变化率，用公式（4）表示：

其中，εikt=β2+β4·t+β6·lnLit+2·β8·lnKit代表资本存量的产出弹性，εilt=β3+β5·t+β6·lnKit+2·β9·lnLit代表从业人员的产出弹性，ε=εiktεilt代表总规模弹性，Sikt=Cikt/(Cikt+Cilt)  、Silt=Cilt/(Cikt+Cilt)代表各要素的成本额。

根据以上推导，可以计算各区域历年来的要素配置效率。在本文中，衡量各区域要素分配效率的主要因素包含为四个变量：活动内部支出存量、国外研发资金、进口贸易中含有的国外研发资金和进口贸易蕴含的国外存量。

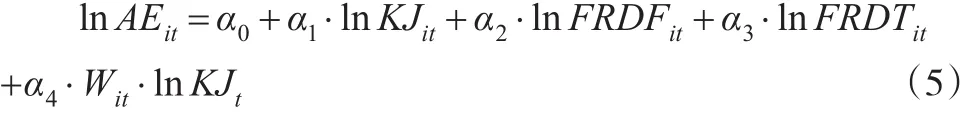
考虑到2006年前后，统计口径发生了变化，导致各区域科技活动经费内部支出量出现差异。为了测算需要，本文把该年度虚拟变量默认为1，并且其他的年份虚拟变量设置为零。用公式（6）表示：

假设AEi0是各区域初期的要素配置率，那么就可以按照模型研究要素配置率的变化率，如公式（7）所示：

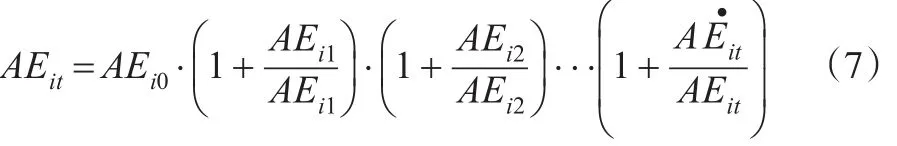
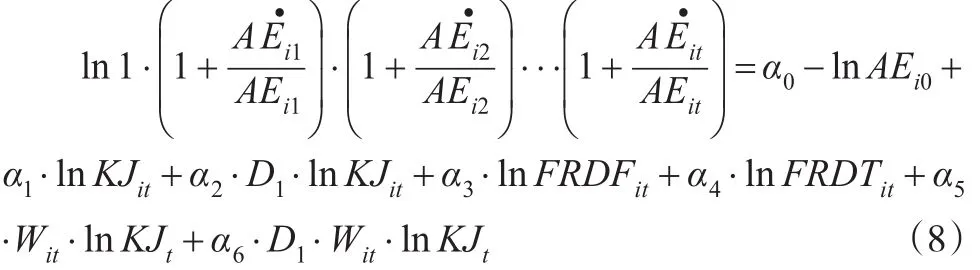
公式（8）可以分解为资本配置效率变化率和劳动效率变化率，并通过要素配置效率变化率得到公式（9）和公式（10）：

2 数据说明和变量分析

本文的数据均来源于《中国统计年鉴》、中国网和中宏网。通过选取不同区域、省市相关指标得到相关数据：各省份历年的GDP数据通过将各地名义GDP除以相应GDP平减指数得到；各省份各年资本存量成本，可以通过将该省的资本存量乘以相应年份的长期贷款平均利率，再加上资本存量的折旧率计算得出；GDP是劳动者收入和资本收入的和，通过将GDP分解为劳动和资本两项，可以分别得到劳动和资本成本；各区域科技活动资金内部支出的计算为该地区科研活动内部支出；人均资本存量和人均财政支出通过将该省的总资本存量和总财政支出除以人口数据得到。财政支出占GDP比例通过将财政支出数据除以当地年度GDP得到，出口及进口贸易额占GDP比重也用同样的方法得到。

如公式（11）所示，本文利用Lichtenberg-Pottelsberghe模型分析进口贸易蕴含的国外存量权重，用公式（12）来表示：

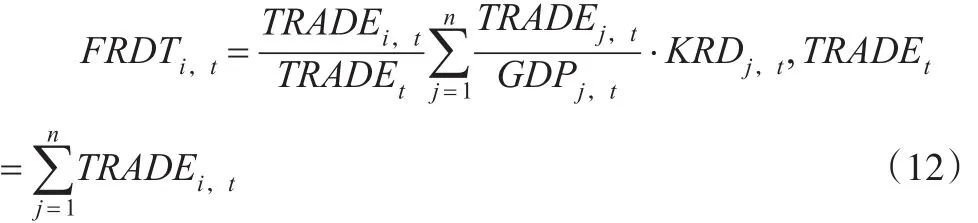
在本文中，将不同地区之间的区域路程当做空间相关阻力因子，并对人均科技活动内部支出绝对值取倒数当做引力因子，创建空间相关矩阵。本文构建的空间关联矩阵为:公式（13）中，地理距离用dij表示，KJi，t=(1/t1-t0=1)·用来表示科技活动经费内部支出量积累值的平均值用。

3 要素配置效率的测算及分析

本文利用随机边界模型和相关指标数据进行研究，估计超越对数函数的参数。超越对数生产函数的参数估计结果见表1。考虑每个区域的要素配置变化率不需要考虑技术无效率方程，因此技术无效率方程的参数估计结果在表1中并未显示。

表1 超越对数生产函数分析结果

表1的估计结果表明超越对数函数各参数均在5%统计水平上显著。根据估计得到的超越对数生产函数并结合各地区资本和劳动占经济中的份额参数，可以得到资源配置效率变动趋势图（见图1）。

图1 全国要素配置效率变化图

根据图1可以发现：全国要素配置效率从2002年开始逐渐上升，2011年则开始出现下降趋势；要素配置变化率在2015年之前均为正，2015年后变为负值，这和最近几年我国经济增长放缓相对应；劳动配置效率变化率的转折点出现在2008年，在这之前劳动分配变化率都是呈缓慢增长走势，2008年劳动配置效率变化率开始呈下降趋势，这和该段时间我国劳动者报酬占GDP比重下降相一致。此外全国要素配置效率变化率的有以下两个特点：一是资本配置效率变化率对要素配置效率变化率起决定作用，要素配置效率在资本配置效率的一定范围内增减；二是全国要素配置效率变化率的波动趋势和劳动配置效率变化率相对应。

基于全国要素配置效率变化率，本文对模型（1）至模型（3）选择残差检验（见表2），但是用ModifiedWald方法进行残差检验发现也存在异方差性。

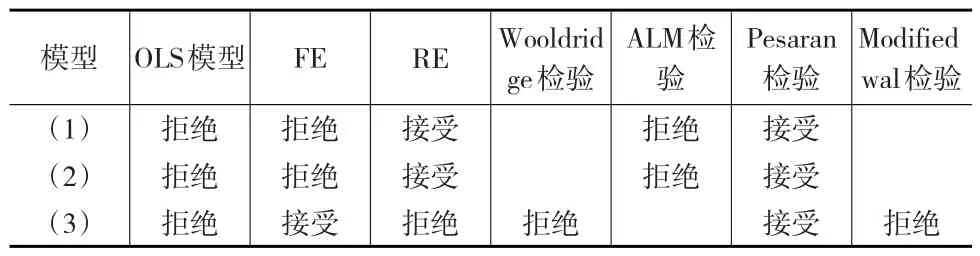
表2 确定模型以及残差检验结果

根据表2，本文采用可行最小二乘（FLGS）对各模型进行估计，估计结果如表3所示。

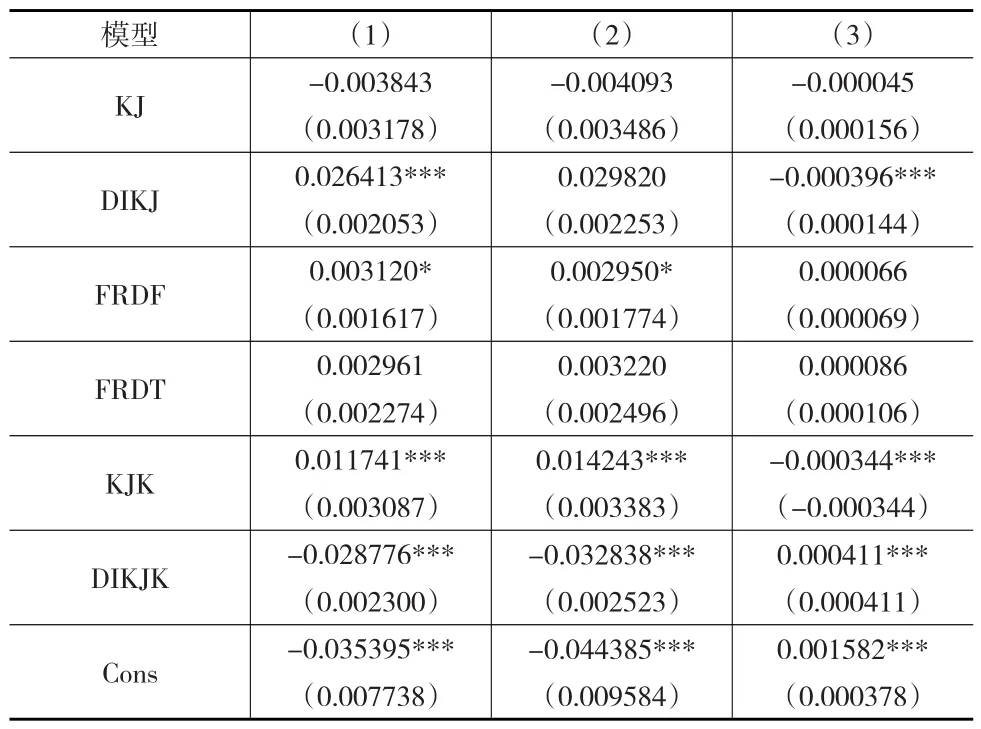
表3 模型的估计结果

从表3中可知，科技活动经费内部支出存量对要素配置率、资本配置率以及劳动配置率都会产生统计上不显著的正向影响，各地区的FRDF（各省历年FDI蕴含的国外R＆D存量）和FRDT（进口贸易蕴含的国外R＆D存量）也都对要素的配置效率起到积极作用。2000年以来，KJK（科技活动经费内部支出存量的空间溢出）对各地区的要素配置率和资本配置率具有显著提高作用，但对劳动配置效率则有着负向影响。

4 结论

本文将劳动要素主要分为普通劳动和人力资本，利用随机前沿超越对数、生产函数模型以及对应的分解技术，建立了“要素价格—要素配置效率—TFP”之间的逻辑分析框架。选取不同区域省市的相关变量，研究要素价格会给要素配置效率以及全要素生产率带来的影响。所得结论如下：

（1）最近几年全国的TFP增长率出现持续下降，TFP增长率下降的主要原因是要素配置效率呈负增长。研究表明我国劳动配置效率多年来保持稳定，生产要素配置效率的下降主要由资本配置效率下降导致，2011年后我国资本配置效率持续下降，对此可能的原因为次债危机后我国为了保持经济稳定，大量的信贷资源流入了相对低效的房地产和基础设施建设，导致资本生产要素的错误配置，于此同时，很多相对效率较好的民营企业却贷款困难，这些因素导致了资本配置效率下降和全要素生产率的下降。

（2）要素价格对于要素有效配置起着重要作用，随机边界模型的分析结果和相关模拟表明我国资源价格存在一定程度的扭曲，物质资本价格相对较高，人力资本价格则比较低。模拟研究发现在保持相关要素数量不变的前提下，降低有形资本相对价格，提高人力资本价格，特别提高普通劳动力的相对价格，可以促进生产要素的分配效率，推动全要素生产率的增长。

（3）要素价格给要素分配效率带来的影响主要体现在成本份额，但是成本份额却又由要素的价格和要素投入的数量决定。中国近10年来的要素分配的效率一直呈负数增长，劳动收入所占GDP份额不断下降，资本收入份额不断上升，这是导致我国收入差距劳动的重要因素。主要的原因在于生产要素价格的扭曲，劳动的价格相对资本较低所致。要素价格的扭曲一方面导致资源配置的无效率，另一方面导致收入差距拉大，未来的经济政策制定应当考虑到该因素。