冰撞载荷下I型夹层板抗冲击性能研究

柴明媚，田阿利，魏 震，马清勇

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

0 引 言

全球气候变暖使得很多地区多年冰的比例逐年下降，每到夏季北极海域经常充满了很多浮冰，打开了一条与世界互通贸易的大门。同时北极海域蕴藏着丰富的油气资源，不论是交通运输还是油气资源的开采，都对船舶在极地地区的航行安全提出了很高的要求，世界各国的研究人员对船冰碰撞问题的研究投来了更多的重视目光。

研究船冰碰撞的关键前提是冰材料的本构模型，不一样的环境条件下冰的力学特性有着很大的差异，因此，国内外学者尚未对冰材料研究有一个准确的定论，其研究一直是一个热点。李洪升等[1]研究了辽东湾的海冰在不同的应变率范围内表现出不一样的力学行为和强度特征，得出结论：不同的应变率下海冰具有不同的本构模型。LIU Zhenhui等[2]在压强和应变率方面对冰的材料模型进行研究，提出冰的材料模型与压强无关，与应变率有关。在冰材料模型逐渐完善的基础上，船冰碰撞的研究也取得了丰富的成果。WANG Bo等[3]运用动态有限元软件 DYTRAN对LNG船与可压碎冰的碰撞动态响应分析，结果显示，加载位置的不同会使船体结构中不同的组件遭到破坏。JIA Zhibin等[4]分析了不同的船速、不同形状的浮冰对船舶舷侧结构与冰的碰撞动态响应。

传统的提高船舶耐撞性能的方法是增加钢板的厚度或敷设装甲，而这样不仅增加了船体重量，使得船舶的载重能力减小、航行速度降低，而且也对军用船舶的作战性能和商业船舶的经济性有所影响。为满足船舶轻量化要求，国内外学者们将目光转向新型复合材料及新型结构。以往的研究可以知道，I型金属夹层结构的使用可以使船舶的总质量和制造工艺成本有所降低[5]。新型夹层结构良好的抗冲击性能、高强度等特性，使其在船舶结构制造中的应用前景十分广阔[6–7]。

本文以船用I型金属夹层板为研究对象，运用理论与数值方法开展冰撞载荷作用下夹层板抗冲击性能的研究，首先采用文献[2]中给出的冰体材料模型，建立I型夹层板-冰碰撞的有限元仿真技术，分析不同条件下的冰撞载荷下夹层板结构的动态响应。通过对冰载荷作用下传统板架结构和金属夹层板结构的抗冲击性能对比，表明金属夹层结构的应用优势。并重点对比分析了不同的冰撞载荷，如撞击位置、冰体形状等对夹层板结构响应的影响规律。

1 夹层板-冰碰撞的数值仿真模型

1.1 冰体材料模型

由于不同的海域及不同年干的冰体材料特性不同，相比其他材料其研究的困难程度有所增加。在海冰的研究领域中，普遍认为当冰体的速度大于0.2 m/s，冰的应变率高于10–3m/s时，海冰的特性近似脆性破损的线弹性材料特征。本文的数值仿真中，冰体采用弹脆性本构模型，并将材料的失效应变作为评判冰体有无破碎的依据，以此用来模拟在某一条件下冰体的材料特性。

图1 为环境温度–11°C，应变率为 5.5×10–3s–1时，多晶冰的真应力-真应变曲线图[8]。图中UNCONFINED为在无约束力的情况下给出的基本曲线，其余从上往下 3 条曲线分别对应约束压力为34 MNm–2、10 MNm–2和85 MNm–2下的应力-应变曲线。在该应变速率下，无约束试验给出了脆性破坏引起的弹性变形。10 MNm–2的约束压力抑制了这种脆性破坏和相关裂纹，并且允许应力比无约束试验的应力高得多，这就导致了冰体发生塑性破坏。约束压力为34 MNm–2时，得到的曲线位于最上方，整体应力最大，但是对于较高的约束压力，如图中85 MNm–2对应的曲线，其强度值则整体下降。

图1 多晶冰的真应力-真应变曲线σ3[8]Fig.1 True stress-true strain curves of polycrystalline ice[8]

1.2 夹层板结构及材料模型

为分析I型夹层板与冰碰撞的动态结构响应，本文设计了如图2所示的I型夹层板结构模型。I型夹层板结构由上、下面板以及芯层构成。特征参数有：夹层板的长度a、宽度b、上面板的厚度tf、下面板的厚度tb、相邻两支柱间的距离bc、支柱的高度Hc以及厚度tc。边界均为四周刚性固定。结构设计参数见表1。

图2 计算模型剖面示意图Fig.2 The cross section of calculation model

表1 特征参数值Tab.1 Characteristic parameter value

不考虑温度变化对钢材性能的影响，船用夹层板钢材选取Johnson-Cook本构模型[9]，最大塑性应变作为材料失效的依据。材料参数如表2所示。

2 数值仿真及结果验证

为了验证冰材料模型的适用性，计算理想圆台状冰体撞击刚性墙，其压力历程曲线与理论标准ISO曲线[10]及实验结果对比验证。P-A标准理论曲线是由A.C. Palmer 和Masterson等[11]于2009年发表的，后被国际ISO标准组织收录到ISO/CD19906(2010)中，并被推荐为冰载荷计算的设计标准。其关系式为：

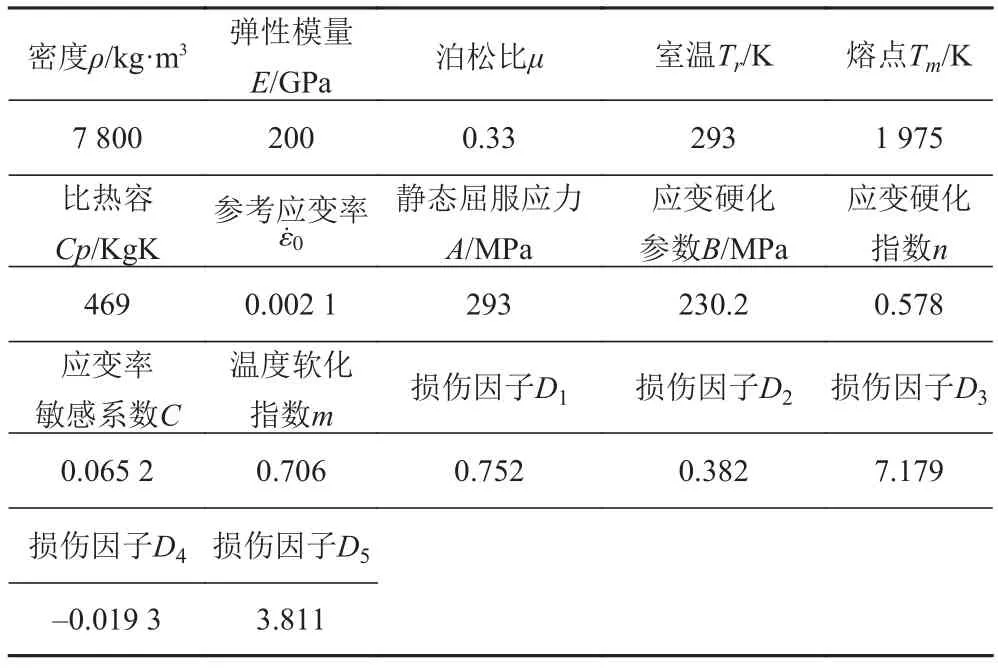
表2 A3钢材料参数Tab.2 Material parameters of A3 steel

式中：P为压力；A为接触面积。

图3为数值仿真结果与ISO理论曲线和实验结果[12]的比较。ISO理论计算公式和本文仿真中并未考虑开始阶段的碎冰堆积所产生的反力作用，所以在开始阶段相同的接触面积下，实验结果高于理论值。在A＜1 m2范围内，仿真结果和实验结果都表现出急剧下降的趋势。在1 m2＜A＜2 m2之间压强表现为在2.7 MPa左右波动。在2 m2＜A＜4 m2之间曲线比较靠近理论曲线和试验曲线，直至A=4.7 m2处曲线结束，仿真曲线表现为最后一点较低。从图中可以看出仿真结果的撞深较小，这与文献[13]的结果相符，主要是由于冰体的弹脆性本构模型未考虑应变率的影响，图中数值模拟结果与实验结果和ISO理论曲线吻合较好，且压力随面积的变化趋势也与二者一致，认为本文的数值仿真技术及所选的冰体材料模型与参数，可以用于模拟实际冰载荷。

3 冰撞载荷下夹层板抗冲击性能讨论

3.1 夹层板与单层板抗冲击性的对比

图3 仿真结果和相关数据的压强-面积曲线比较Fig.3 The comparison between simulation resultand and cited data

在船冰相互碰撞作用中，评判船用结构耐撞性能的依据主要有：船体结构的破坏变形情况、船体外板能够承受的碰撞力大小和船体各结构的能量吸收情况等。在相同的碰撞深度下，结构所能承受和抵抗的碰撞力越大，认为结构的刚度越大，耐撞性能越优。在不同的碰撞方案下船体结构因发生变形而吸收的能量大小可以作为衡量船舶的变形程度及受损情况。

表3给出了单层板和夹层板在碰撞中相同的撞深下所承受的碰撞力以及能量吸收的最大值的对比，其中单层板和夹层板的尺寸根据等质量原则确定，从表中可以看出，在撞深都为0.4 m时，单层板受到的碰撞的作用力为2.5×106N，夹层板受到的碰撞载荷为4.5×106N，相比之下夹层板比单层板所承受的碰撞力大，表明夹层板的结构刚度大，在相同条件下的耐撞性好。从能量吸收来看，夹层板能量吸收的最大值为1.19×106J，相同条件下单层板的最大吸能为1.17×106J，夹层板的吸能水平要高，吸能水平高会使冰体的动能减小，对结构的损害减小。综合所述，在相同条件下认为夹层板比单层板的抗冲击性能好。

表3 结果对比Tab.3 Comparative results

3.2 撞击位置对夹层板结构响应的影响

冰体为正立方结构，以10 m/s的速度撞击夹层板两处典型的位置：夹层板两芯材焊缝中间点（工况A）；夹层板芯材焊缝处（工况B）。图4为夹层板与冰碰撞在 2 种模拟工况下的有限元模型图。

图4 碰撞区域的有限元模型图Fig.4 Finite element model of collision position

1）碰撞的损伤变形

图5为夹层板的损伤变形图。在碰撞进行到0.1 s时 2 种工况下冰体均发生了反弹，由于速度过低加上模型质量有限，船体外板均发生了弹性变形和塑性变形而未发生破裂，工况A的变形面比工况B平缓，这是由于工况B冰棱正好作用在夹层板腹板上，腹板对下面板力的传递作用使得下面板变形比较尖锐，此情况也容易发生应力集中现象。

图5 夹层板碰撞区域损伤变形图Fig.5 Damage Deformation Diagram of Sandwich Plate Impact Area

图6为冰体的损伤情况。从图中的 2 种工况可以看出，立方形冰体靠近碰撞区的一条棱边上均受到了不同程度的破损。对应于工况A，由于夹层板两芯层腹板之间的距离小，碰撞在进行一段时间后 2 个芯层也对外板起支撑作用，并且由于两芯层外板板材的弹性作用使得碰撞出现的时间较长（0.065～0.09 s），导致碰撞力较大冰体的破损出现在整条棱边上。工况B的撞击位置在芯层焊缝处，当其与冰体接触瞬间，结构局部刚度较大，因此撞击力迅速上升到最高点而后由于芯层的抵抗作用撞击速度减小冰体出现反弹，整个碰撞中只有棱角处的冰体达到失效条件发生破损。

2）碰撞力

图7为A工况、B工况下夹层板所受的碰撞力随时间改变的曲线图。图中所表示的是冰体和靠近碰撞区的夹层板外板的碰撞力曲线图，总计算时间为0.25 s，2 种工况的碰撞力在0.12 s附近均消失，所以只取0.15 s以前的曲线。对应于工况A，首先远离碰撞区域的外板起主要作用抵抗外载荷发生变形，在0.065 s时刻，碰撞力达到最大值5.7×106N，碰撞力出现一次加载现象，而后又卸载，0.07 s左右芯层起主要作用，碰撞力先增加很快又减小，0.09 s时刻靠近碰撞区域的外板起主要抵抗作用，碰撞力再次增加又减小，直到0.12 s夹层板和冰体分离，碰撞力完全消失。对应于工况B，由于芯层腹板对外板的支撑作用外板和冰体在0.06 s时刻碰撞力已达到最大值5.7×106N，其值基本与工况A相等，时间提早0.005 s，然后碰撞力下降，到0.08 s靠近碰撞区的外板起主要的抵抗作用，碰撞力又开始上升，到0.09 s冰体与外板逐步分开，碰撞力开始下降直到0.12 s附近完全消失。

结合以上分析可以发现，对于棱边正对夹层板芯层焊缝处的冰体，夹层板芯层的抵抗作用比较明显，整个碰撞过程中夹层板所承受的碰撞力水平较高，这主要是因为当碰撞部位在夹层板的加强位置时，构件会有明显的抵抗作用，结构的刚度也就大，耐撞性能好。

3）能量吸收

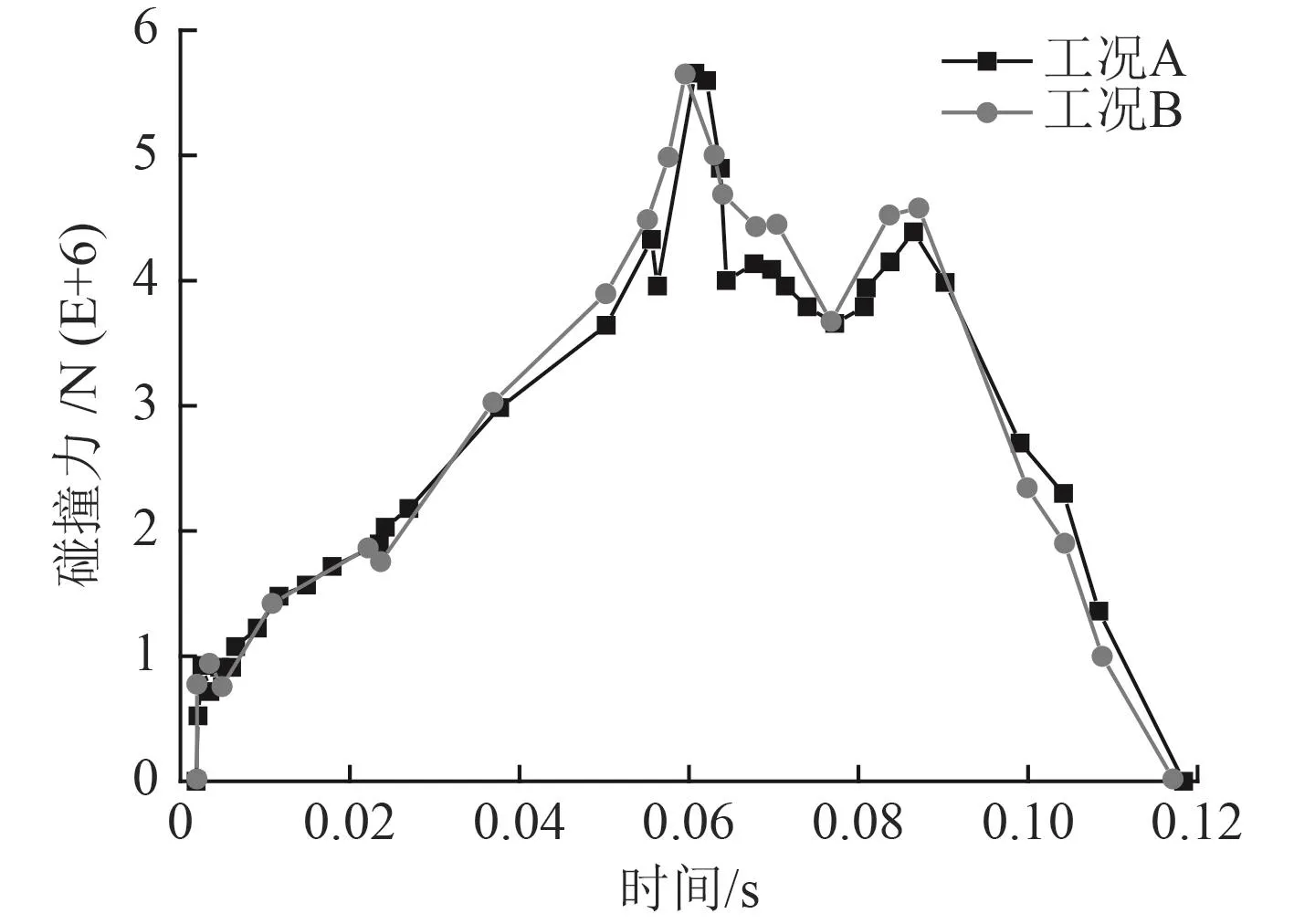
图7 两种工况下碰撞力-时间变化曲线Fig.7 Curve of collision force-time under two conditions

图8为不同的工况碰撞下夹层板结构的总吸能随时间变化的曲线图。对应于工况A，0.08 s之前是夹层板与冰体碰撞的前期，由于夹层板两支柱对外板的支撑作用，使得结构有力地抵抗了外部载荷，此过程中结构的吸能增长迅速，在0.08～0.12 s之间，冰体反弹，能量开始释放，一部分内能转化为机械能，0.12～0.25 s之间，冰体和夹层板之间分离，两者之间不再有力的作用，吸能曲线趋于平坦。对应于工况B，夹层板与冰体在碰撞前期，夹层板支柱对冰体的碰撞产生强有力的抵抗，能量的吸收增长速度快，比工况A要高，在0.08～0.12 s，冰块同样反弹，能量开始释放，一部分内能同样转化为机械能，0.12～0.25 s之间，两者不再接触，吸能曲线趋于平缓。

图8 结构总吸能历程曲线Fig.8 Structure total energy absorption curve

从以上分析可以看出，工况B比工况A整体的能量吸收能力高一些，表明芯层腹板是比较重要的吸能构件，也证实了夹层板的芯层部分在整个构件加强中的重要性。

3.3 冰体形状对夹层板的吸能影响

本节根据不同的冰体形状提出并模拟 2 种工况。工况Ⅰ选用立方形冰体撞击夹层板，工况Ⅱ选用球形冰体撞击夹层板。控制 2 种冰体重量相同。冰体以6 m/s的速度迎面撞击夹层板。碰撞的有限元模型如图9所示。

图9 碰撞的有限元模型Fig.9 The finite element model of collision

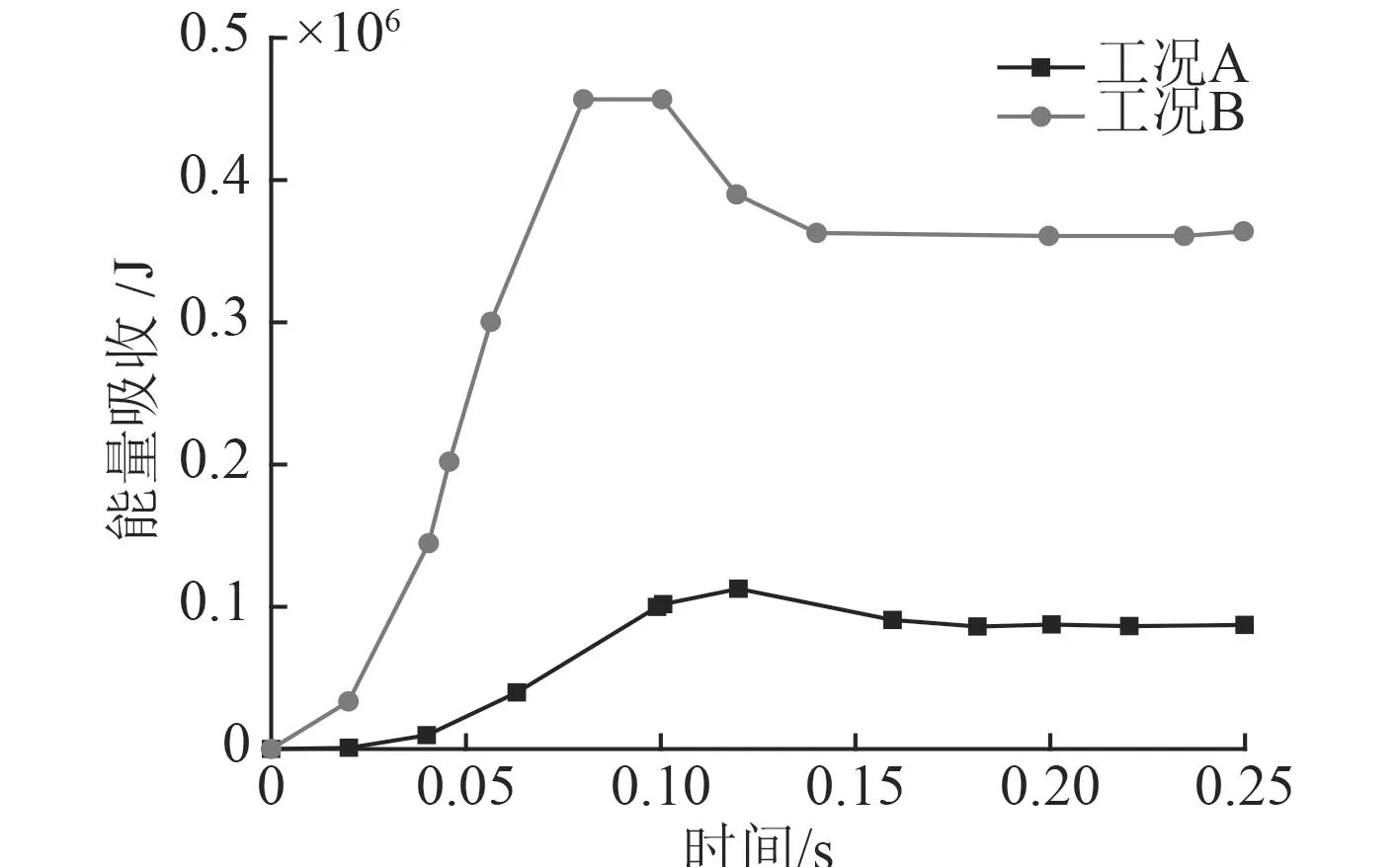
图10 结构总吸能-时间历程曲线Fig.10 Curve of total energy absorption-time

图10为Ⅰ和Ⅱ两工况的碰撞下夹层板结构的总吸能变化曲线图。可以看出，在0.1～0.12 s之间，由于接触面积的不同，工况Ⅱ的结构吸能远高于工况Ⅰ。碰撞刚开始时，由于冰体与夹层板接触，2 种工况的吸能曲线都有不同程度的上升，工况Ⅱ比工况Ⅰ的斜率大，能量吸收增加速度快，伴随着冰体撞击夹层板的继续深入，2 种工况冰体都出现反弹，吸能都开始下降，能量开始释放，一部分内能转化为动能和势能，直至冰体与夹层板分离，吸能几乎不变为止。

结合上述分析可以看出，在撞击速度和撞击位置相同的情况下，球形冰体比立方形冰体对夹层板碰撞的吸能能力要高，球形冰体比立方形冰体与夹层板之间的接触面积大，导致碰撞的延伸性，夹层板吸能面积增多，吸能能力也就相应增加了。

4 结 语

本文提出了适用于船用金属夹层板和冰碰撞的冰材料模型，用于数值仿真模拟，并对该模型验证，将它应用于I型夹层板-冰碰撞时对夹层板结构的响应进行研究。主要结论如下：

1）本文运用冰体与刚性墙的碰撞实验验证了冰材料模型的适用性，将仿真结果与ISO推荐曲线的经验公式及试验数据作比较，结果显示三者吻合较好，证明本文提出的材料模型可以用于研究冰和夹层板碰撞的仿真模拟中。

2）根据等质量原则，对传统单层板与新型夹层板在相同撞深下的碰撞力和能量吸收的最大值进行对比，得出夹层板所能承受的碰撞力大于单层板，其耐撞性更优，且夹层板的吸能水平大于单层板，对外部载荷的抵抗能力更强，认为夹层板比单层板的抗冲击性能好。

3）冰体撞击位置的不同，对夹层板所能承受的碰撞力及能量吸收有不同的结果。没有支柱支撑的夹层板结构所能承受的碰撞力的最大值基本和有支柱支撑的夹层板相等，整体碰撞力水平后者略高，能量吸收情况则正好相反，但趋势基本一致。

4）不同的冰体形状撞击夹层板，夹层板的能量的吸收和分配情况则不同。在冰局部形状较尖锐的条件下，夹层板结构总体吸能比较低，在冰局部形状比较平缓的接触面下冰体近为刚体性能，那么夹层板的总体吸能相对要高。