基于拖曳线列阵声纳与ARPA雷达的目标分选
高枫,颜明重,朱大奇
(上海海事大学信息工程学院,上海201306)
拖曳线列阵声纳是一种拖曳距船尾部一定距离的声波接收系统,用于探测水上与水下目标。它通过接收航行目标自身辐射噪声来进行探测,标定,跟踪以及类型识别[1]。
拖曳线列阵声纳技术虽能用于测量目标的方向,但其在水上与水下的目标分选工作中仍存在不小的局限性。目前,利用拖曳线列阵声纳进行目标分选的研究中,通常采用对探测目标的辐射噪声进行特征提取的方法,获得探测目标辐射噪声的功率谱、频谱,并与现有船艇噪声库和信息库进行对照分析,从而实现目标分选[2]。但由于水声目标本身种类繁多、目标辐射噪声随海情、航速、工况的不同而变化及各种客观因素的影响,即使是同一目标辐射噪声的差异也很大,并且水声样本是各个国家的机密,因此,拥有完备的信号库是十分困难且代价很高的[3-4]。所以,对于信息库中未记录辐射噪声频谱的目标,无法用此方法对目标进行识别或分选。
为解决这种拖曳线列阵声纳目标分选工作的局限性,本文充分利用拖曳线列阵声纳与其他传感器,如船载的ARPA雷达,采用信息融合的方法,来实现水上与水下目标的分选。由于ARPA雷达只能探测到水上目标[5-7],而拖曳线列阵声纳可同时探测到水上和水下的目标,因此,将拖曳线列阵声纳与ARPA雷达的多目标数据进行时空配准和航迹关联,可有效地分选出水下目标。
本文主要工作如下:通过构建实际运动仿真模型,对同时载有拖曳线列阵声纳与ARPA雷达的舰船基于分布式结构模型进行具体目标分选分析。主要步骤包括:时间配准、空间配准及航迹关联。其中,本文使用自适应α-β算法进行ARPA雷达与拖曳线列阵声纳数据的时间配准,采用基于统计的最近领域法进行航迹关联。
1 运动目标建模
拖曳线列阵声纳探测系统与ARPA雷达系统所探测到的方位是目标相对于本船的角度,设原点为本船,目标与本船的相对位置如图1所示。

图1 探测目标角度示意图
以正北方向为零度方向,进行顺时针旋转,α表示目标相对本船的绝对方位,β表示本船的航向角,则声纳基阵探测到的目标方位θ可以表示为:

即,考虑的方位就是对θ的计算,当本船保持类直线运动或停滞不动时,本船航向β是一个常数。θ与α是线性关系,对探测方位的计算可以转化为对绝对方位的计算。
不同的目标运动模型在声纳图上显示的航迹是不同的。设想一个目标围绕着本船做类圆周运动(曲线运动),如图2所示:
目标相对拖曳阵声纳基阵的方位角表示为:

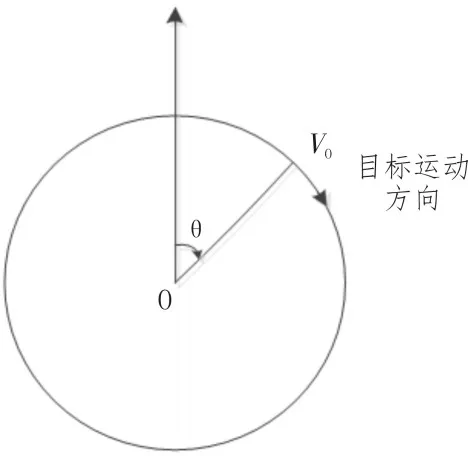
图2 类圆周运动模型图
其中:θ0为目标初始方位,R为目标做类圆周运动的半径,V0是目标转向角速度,V为本船速度。当速度V较小时,探测方位θ与时间t的关系近似为线性关系。若目标保持类直线运动,如图3:

图3 类直线运动模型图
目标相对探测基阵的方位角可表示为:
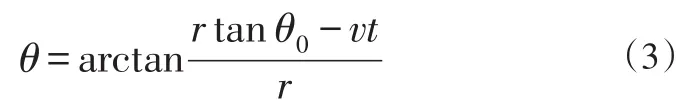
若它不是t的线性函数,目标方位轨迹会显示为一条正切曲线,根据已有的目标方位记录值进行正切函数计算是非常困难的,会消耗大量的时间。最有效的办法是假设目标的方位角在短时间服从线性变化,根据已知的目标航迹(t,θ)利用最小二乘方法拟合出一条直线,计算某个时刻的θ值,设:

求a,b使得J极小,再对J求微商:

可解得:

其中:

把a,b代入公式,可求得:

在短时间内,水上与水下运动目标的方位角可看作呈线性变化的。这种类直线拟合的方式,时间越短效果越好。因此,在短时间内探测海上运动目标时,可将目标方位角看作呈线性变化。
2 目标数据预处理
2.1 目标数据空间配准
由于声纳基阵中心与母船雷达的坐标中心位置不同,因此,在航迹关联之前,需对空间坐标进行统一。一般将拖曳线列阵声纳测得的目标方位,经视差修正,转换到母船雷达坐标系中[8],如图4所示。

图4 拖曳线列阵声纳探测目标示意图
假设本船拖曳线列阵声纳长L米,本船雷达的位置为O,目标位置为Ot,目标距离声纳中心θs的距离为D,拖曳线列阵声纳探测的舷角为θ,则修正后的舷角为:

2.2 目标数据时间配准
拖曳线列阵声纳与ARPA雷达的目标数据传输率通常不一致,在航迹关联前,必须对其在时间上进行同步。常见时间同步方法有:最小二乘法、内插外推、基于神经网络的一系列算法和滤波算法等[9-13]。本文采用一种在时间复杂度和空间复杂度都较小,更加满足实际应用的自适应α-β滤波算法。
一般的α-β滤波算法精度不够高,并且往往随着目标运动的变化误差会越来越大,不能满足信息融合要求,本研究使用的自适α-β算法,用残差累积的方法来不断更α,β值,从而将其精确度提高[14],下面给出公式说明:

其中:XP(K)是通过前一个周期即第K-1个周期,来预测的目标信号在第K周期的横坐标测量值,Xc(K) 是目标在第K周期的横坐标计算值;αX(K)是第K周期X方向的距离平滑系数,βX(K)是第K周期X方向速度分量的平滑系数。
加入修正系数是因为预测值或计算值存在误差。若将α,β设为固定值,当目标船发生运动状态变化时,很容易造成轨迹预测错误。此处采用残差积累算法不停更新α,β值,残差用来表示,传感器的测量误差的方差用来表示,该误差是固定值。而预测的误差需要一个过程去积累,因此我们需要一个滑动窗口来不停更新。对于数据的处理我们仅需考虑一个方向即可。下面以X方向的α,β计算为例。

3 目标航迹关联
航迹关联的主要工作可以描述为:预处理过后的ARPA雷达目标数据和拖曳线列阵声纳目标数据是否源于相同目标,同源目标即为水上目标,非同源目标则为水下目标。
多传感器多目标的航迹关联算法通常分为基于统计算法的和基于模糊数学的算法[15-16]。理论上,基于模糊数学的关联算法具有精度高,关联误差小的优点,尤其是在目标数量大且目标数据分布密集的情况下。但这是以牺牲时间、空间复杂度为前提的。基于统计的关联算法虽然在目标数量大且目标数据分布极为密集的情况下,精度不如基于模糊数学的关联算法,但在效率上要远远高于前者。本文考虑在实际应用中目标的分布不会过于密集,而且实际往往要求时间和空间复杂度更小的算法,因此采用基于统计的算法。先不妨假设节点数为M=2,对于M>2的情况可以类推,设两个传感器的航迹节点集合分别为:

可定义H0和H1为下列事件:是对于相同 目标的航迹估计;H1:是对于不同目标的航迹估计。这样目标关联问题就转化为了假设检验问题,这里我们使用最近邻域法。
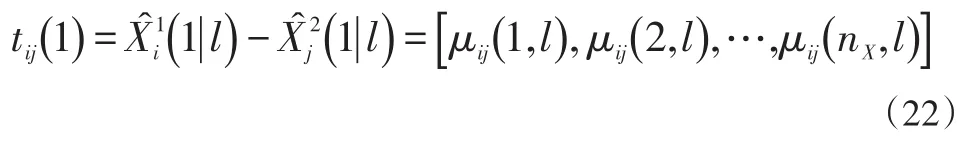
式中:i∈U1,j∈U2,nX是状态估计的维数,表示l时刻的各航迹的状态估计误差。若假设阈值矢量为,那么,最近领域关联的标准为:
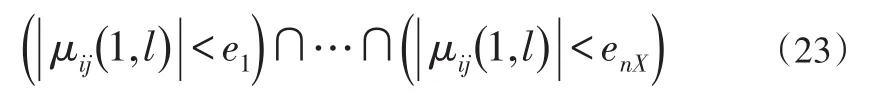
若公式(23)成立,那么我们就可认为两条航迹相关联,且只要成功关联,就无需对该航迹进行后续关联检测。也有学者提出了基于统计的其它算法,这里不再赘述。
4 仿真与实现
4.1 时间配准算法仿真
针对上述两种时间配准算法,本节采用MATLAB软件对其进行仿真与分析,模拟目标的运动轨迹与ARPA雷达获得的数据测量值。再用两种时间配准算法对该数据进行处理,比较二者的配准精度。误差取时间点为5到50秒的配准数据与真实数据的差值绝对值,如图5~7所示。

图5 时间配准局部放大图

图6 卡尔曼滤波算法误差分析图

图7 自适应α-β滤波算法误差分析图
通过分析可知,一方面,在精度上,自适应的α-β滤波算法能够将误差范围控制在0.4度以内,而常用的卡尔曼滤波算法只能将误差范围控制在0.6度以内。由此可见在实际应用中,自适应的α-β滤波算法与目标实际运动轨迹的匹配度更高,且计算量更小,时间和空间复杂度更低,因此,运行所占内存小,速度更快,能够在尽可能短的时间内对目标进行分选。另一方面,自适应α-β滤波算法能够根据经验设置初始α,β值,使轨迹尽快趋于收敛,而卡尔曼滤波算法的初始误差极大,需一段时间后才趋于收敛。因此在实际应用中,自适应α-β滤波算法更满足实际需求。
4.2 时间配准算法的实际应用
将自适应的α-β滤波算法应用到一组真实数据中,本文选取了一段从100s到500s的时间范围内,目标真实运动轨迹的方位角数据,如图8所示。
由分析可知,虽然真实数据会随着测量误差上下浮动,但浮动幅度极小,可在大体上保持稳定。对比ARPA雷达数据与拖曳线列阵声纳数据的时间序列,按缺少的时间的值在滤波之后的函数上取值,即可达到时间配准的目的。
4.3 航迹关联算法仿真
针对上述的关联方法,利用MATLAB进行仿真验证,模拟了3个目标,两个水上目标,一个水下目标,用时间配准后的ARPA雷达数据和拖曳线列阵声纳数据进行关联,见表1~3,从而判断目标位置,完成分选。

图8 真实数据配准图

表1 阈值e=1°时的关联率

表2 阈值e=0.75°时的关联率
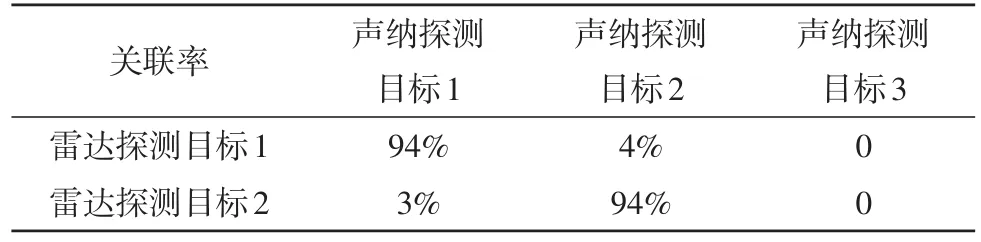
表3 阈值e=0.6°时的关联率
由表1~3可知,拖曳线列阵声纳探测到的目标1和ARPA雷达的目标1是同一目标,拖曳线列阵声纳探测到的目标2和ARPA雷达的目标2是同一目标,而目标3则是水下目标。且由表中数据可知,关联率对于阈值的取值并不敏感,可通过经验取阈值。由于个别探测点的测量误差较大,还存在两船探测轨迹交叉的情形,在交叉点附近易发生误关联,但对于关联率90%以上的两个目标,可认为这两个目标为同一目标,声纳数据图与雷达数据图分别如图9与图10所示。
5 结论

图9 声纳数据图
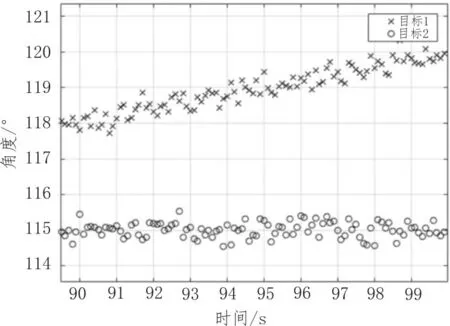
图10 雷达数据图
鉴于我国现阶段水上与水下目标的分选研究具有依赖已有噪声库这一局限性,本文设计了基于拖曳线列阵声纳和ARPA雷达的目标分选系统,使其不必依赖于信息库中的数据。该系统使用分布式融合模型对运动模型进行分析,模拟了真实船舶的拖曳线列阵声纳数据与ARPA雷达数据,采用了优化的时间配准、空间配准和航迹关联算法,具有更小的时间复杂度与空间复杂度以及更高的精度,因此,其所占内存小、运行速度快,更加满足实际应用要求。通过MATLAB软件进行的仿真实现和测试验证表明,本文提出的方法能够快速且可靠的对未知目标进行初步分选,在实际应用中,可借此方法分选陌生船只或潜水器,这对于我国的国防建设有着十分重要的实际意义。本文研究不仅局限于拖曳列阵声纳与ARPA雷达这两个传感器,也可加入AIS等探测设备,即本文后续研究可拓展至多传感器。

