博弈论分析下的上市公司会计舞弊与监管研究
牛东武
(南京航空航天大学财务处,南京 210016)
1 引言
会计舞弊是会计主体对实质性和重要性会计事实等会计信息进行故意瞒报、谎报、错报的一种行为。本文采用经济数学中的博弈论分析和技术经济学原理,重新审视上市公司在监管部门下的信息披露质量,构建上市公司和财务监管部门的博弈体系和相关模型,探讨上市公司会计舞弊与相关部门的监管关系。
2 会计舞弊原因分析
第一,制度性原因,包含:缺乏遏制会计舞弊行为的有效内部控制制度;监督失效的内部环境;信息不对称。第二,上市公司高层管理人员个人利益的驱使,为了确保职位或追逐短期经济利益而进行财务舞弊。第三,上市公司自身特定利益的驱动,以维持公司形象。这是因为,上市公司股价与经营状况、成长业绩、管理者决策水平以及信息披露水平等呈正相关。第四,上市公司股权融资与再融资动机,以带来较为充足的现金流,有助于实现规模扩张。第五,政府对上市公司的暗下操控与干预,进而满足当地政府或领导的政绩和私欲。第六,财务会计人员职业道德低下。
3 上市公司财务部门与政府监管部门的博弈模型建立及分析
本文假设:上市公司财务部门只能提供有限的会计信息给政府监管部门;相关监管者拥有有限的精力、时间和监管方法,且监管结果有限。上市公司与财务监管部门博弈目标存在差异;并假设双方作为博弈的参与者均为“理性经济人”[1],追求成本收益下的效益最大化;双方进行的是经典的博弈过程。
通过分析,假设会计主体通过舞弊行为可能获得的收益和可能付出的成本如下表1所示。
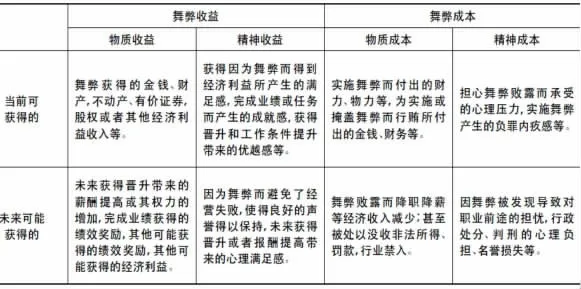
表1 会计舞弊的收益与成本表
在此基础上,针对本文研究的政府监管部门对上市公司会计舞弊行为的监管问题,需再做出如下几条假设:
①策略选择(Strategies):政府监管者监管的两种纯策略为有效和无效;上市公司舞弊的两种纯策略为进行舞弊和不进行舞弊。且双方互不知情。
②上市公司正常收益I1(不舞弊时),额外收益I2(舞弊时),舞弊概率 P2。
③政府监管者对上市公司额外收益进行没收并罚款F。会计监管部门的固定监管成本C。
④政府监管部门空闲收益I3。政府监管部门失职下的社会影响:损失L。可以有效监管的概率P1。
⑤监管的有效性假设:只要政府监管部门能采取相应的监管策略和强度,则一定有效。
⑥政府监管部门的期望函数E政府(P1,P2)和上市公司的期望函数 E政府(P1,P2)。
因此,上市公司舞弊时,政府监管部门的得益有如下假设:I3-L<-C+I2+F,即有效监管比无效监管有益。
根据以上博弈论的相关假设,构建博弈矩阵:
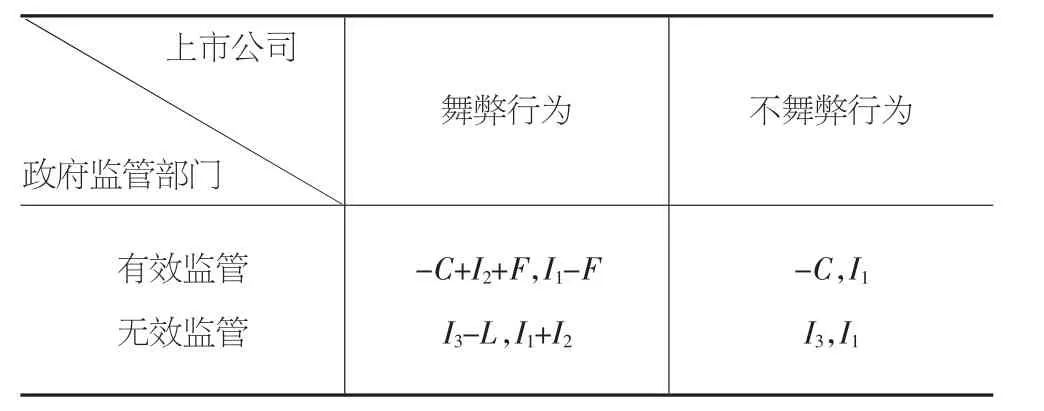
上市公司舞弊行为 不舞弊行为政府监管部门有效监管无效监管-C+I2+F,I1-F I3-L,I1+I2-C,I1 I3,I1
注:其中前者参数代表政府监管部门的收益,后者代表上市公司的收益。
可以看出,当我们不考虑假设I3-L<-C+I2+F时,即当FC+I2≤I3-L(即F+I2-I3≤C-L),即发生的监管成本大于或等于罚没额度时,通过排除严格劣策略,即首先排除监管者的“监管策略”,然后排除上市公司的“不舞弊策略”,即可得出该博弈的纯策略纳什均衡,即为(不监管,进行舞弊)[2]。
如果在 I3-L<-C+I2+F 时(即 F+I2-I3>C-L),说明监管成本小于罚没额度时,该博弈模型不存在纯策略下的纳什均衡,因此可求混合策略下的纳什均衡。
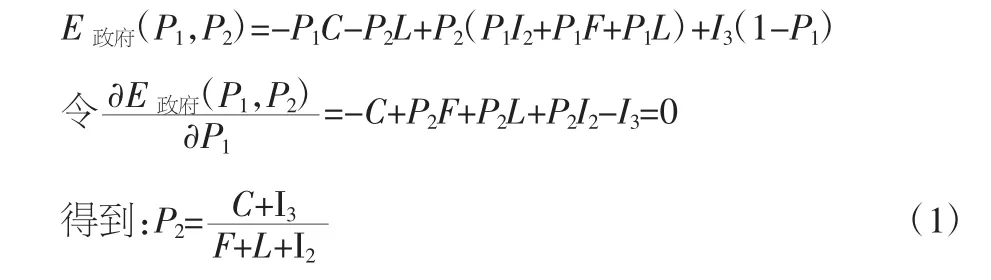
由(1)可知,上市公司进行会计舞弊的概率P2与固定监管成本C、监管部门空闲收益I3呈正相关关系,与会计舞弊处罚F、失职下的社会影响损失L、舞弊额外收益I2呈负相关关系。
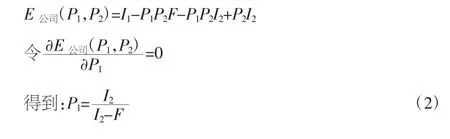
由(2)可知,政府监管部门的监管概率P1与公司舞弊取得额外收益I2、公司舞弊得到处罚F呈正相关关系。这说明加大处罚力度,会提高监管力度;公司舞弊的额外收益越高,也会提升监管部门的监管力度。
4 博弈分析结论对通过政府监管防范上市公司会计舞弊的现实启示
由博弈结果分析可知,这种博弈平衡属于不稳定的、非线性的混合策略纳什均衡,所以通过政府监管不是单一手段就能轻易实现的。通过反应函数法求解博弈模型,可以得到上市公司与政府监管部门的策略选择及其相应的纳什均衡,如图1。
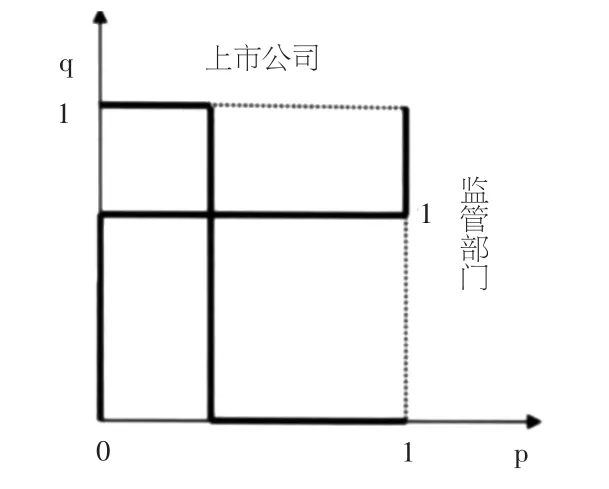
图1 混合策略纳什均衡图示
可知,上市公司进行会计舞弊的概率P2是由政府监管的惩罚力度F和实施监管的固定成本C以及监管部门空闲收益I3决定的,且F越高,舞弊的概率P2越低;但当监管固定成本C与空闲收益I3越高时,上市公司进行财务舞弊的概率P2越大。
因此,可采取如下措施:第一,通过法律及制度建设加强监管力度。第二,降低监管成本,提高企业会计舞弊被发现的概率。第三,加大处罚力度,提高违规成本。第四,加强政府监管部门的管理。第五,加强企业组织诚信文化建设,强化长效机制建设。
5 结语
综上所述,我国上市公司的会计舞弊问题普遍存在,极大干扰了市场的正常运营,本文采用构建博弈模型的方法,在一定的假设约束条件下,探究上市公司与政府监管部门追求各自的最大化效用,并依此求解博弈模型的纳什均衡条件,针对性提出防范上市公司进行会计舞弊的有效策略。

