基于小波树和互补分解的CS-MRI重建算法
裴 颖,朱金秀,杨语晨,吴文霞
(1.河海大学 物联网工程学院,江苏 常州 213022;2.南通河海大学 海洋与近海工程研究院,江苏 南通 226300)
0 引 言
核磁共振成像(magnetic resonance imaging,MRI)是医学成像,应用广泛。目前MRI应用的关键在于快速成像。Nyquist采样定理需两倍带宽,不符合实际应用[1],现常用方法是在压缩感知(compressed sensing,CS)[2-3]框架下,从欠采样k空间中重建MRI数据,能有效减少采样时间,达到快速成像的目的。
关于CS-MRI重建算法的研究有很多。例如,Lusting等[4]利用全变分(total variation,TV)和小波构建目标函数,提出共轭梯度算法(CG),但重建时间有待提高;FISTA算法[5]通过计算更合适的起始点以加快收敛速度;TVCMRI[6]、RecPF[7]和FCSA[8]算法利用算子分割、变量分割思想求解联合正则算子,提高重建速度和质量;文献[9]利用图像在频域的特性优化测量矩阵并提出迭代加权算法,提高了重建精度;文献[2,10]利用MR图像低秩特性进行奇异值分解,但过程过于复杂;文献[11-12]提出结构稀疏理论,图像不仅在小波域有稀疏性,其小波稀疏系数也有特定的四叉树结构,在此基础上文献[13]提出YALL1算法,利用小波树结构稀疏代替小波稀疏构建目标函数,以提高图像稀疏度;文献[14]提出WaTMRI算法,联合小波树结构稀疏和小波稀疏分别拥有的结构稀疏和稀疏性,联合改善图像质量;Park等[15]提出互补分解,将完整图像分为平滑和残差两个分量,仅将平滑分量用于TV,残差分量用于1范数,以解决全变分导致的细节过平滑问题;文献[16]利用贪婪算法提高重建速度,但需要确定图像稀疏度,缺乏实际性;文献[17]基于p范数构建重建算法,计算较为复杂。
重建算法常用小波稀疏和TV构建目标函数,但TV会在滤除噪声的同时平滑图像的边缘纹理信息。因此,文中提出一种基于小波树和互补分解的CS-MRI(MRI based on complementary dual decomposition and wavelet tree sparsity,DualWaTMRI)重建算法,利用互补分解抑制TV造成的细节过平滑问题,小波树结构稀疏用于补充小波稀疏的先验信息,并与同类重建算法进行了对比。
1 基于小波树和互补分解的CS-MRI重建算法
基于小波树和互补分解的CS-MRI重建算法系统框架如图1所示。首先欠采样输入数据得到测量值b,将其傅里叶逆变换预处理生成初始重构图像,再对其互补分解,生成初始残差分量和平滑分量,分别进行TV和1范数处理,同时利用结构化稀疏理论[13],对整幅图像进行小波树结构稀疏处理,最后与最小二乘拟合共同构建目标函数。同时,提出DualWaTMRI重构算法进行求解,分别得到重构的残差分量和平滑分量,由两分量叠加组成最终的重建图像。
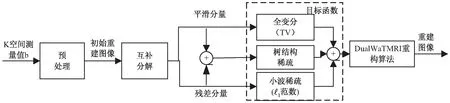
图1 算法系统框架
1.1 基于小波树和互补分解的目标函数
1.1.1 小波树
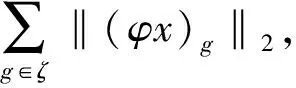
1.1.2 互补分解
考虑到对整幅图像进行TV处理会同时平滑噪声和图像的细节信息,引入互补分解模型[13],将MR图像看成是平滑分量和残差分量的叠加:
x=L+S
(1)
其中,x表示MR图像;L表示灰度值缓慢变化的平滑分量,一般代表图像背景信息;S表示灰度值快速变化的残差分量,一般代表图像中前景信息。
为避免TV过平滑图像,仅对L进行TV处理,S进行小波稀疏处理。文中利用边缘检测算子Sobel[18]对图像进行互补分解,令初始残差分量S0为分解得到的边缘信息,初始平滑分量L0为0。Sobel算子通过核与像素值做卷积和运算,选取合适的阈值提取边缘信息,阈值计算方法为T=μ*255,其中μ是阈值比。
1.1.3 目标函数
综合互补分解和小波树结构稀疏的优势,提出基于小波树和互补分解的CS-MRI重建算法,构建目标函数如下:
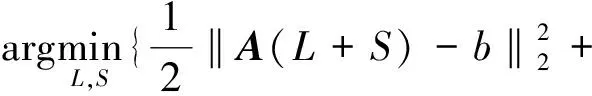
α‖L‖TV+β(‖φS‖1+
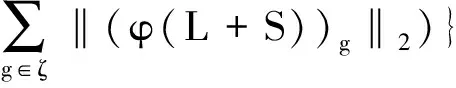
(2)
其中,L,S分别是平滑和残差分量;A是测量矩阵;b是测量值;φ是小波稀疏基;ζ是小波树形分组的集合;g表示其中一组;α和β是调优参数,用于平衡所占比重。式2中第一项最小二乘拟合项用于保证重建图像的准确度,第二项平滑分量的TV项用于抑制噪声,避免图像过平滑,第三项残差分量的1范数用于保证小波稀疏,第四项小波树结构稀疏项用于保证图像的结构稀疏性。这四个正则项相互补充,增加图像先验信息,提高算法的鲁棒性。
1.2 DualWaTMRI重构算法
针对式2中的L和S两个未知量,利用交替最小化方法构建DualWaTMRI重构算法进行求解,将目标函数分为L子问题(此时S为固定值)和S子问题(此时L为固定值),同时将这两个子问题交替迭代,最后重建图像x即是求解得到的L和S值之和。
1.2.1L子问题求解
求解L子问题时,假设S为固定值,则最小化求解时可省略常数项。L子问题公式表示如下:
(3)
为简便求解小波树结构稀疏正则项,令zp=GφL,其中G是ζ的二值矩阵[15],式3改为:
(4)
其中,λ是调优参数;ζ中共有s组g,gi表示第i组g,即第i个具有父子依赖性的小波系数组,i=1,2,…,s。式4中亦包含zp和L两个未知量,采用交替最小化进一步细化:
(1)L子问题中zp未知量按gi分组求解:
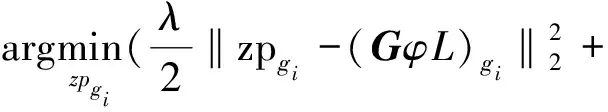
β‖zpgi‖2)
(5)
上式可采用分组软阈值法求解,令rpi=(GφL)gi:
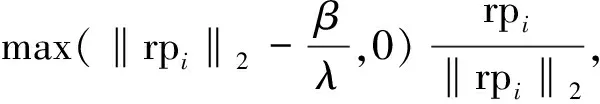
i=1,2,…,s
(6)
由上式求解zpgi值,将其按位置线性组合生成zp。
(2)L子问题中L未知量求解公式如下:
其中,zp值由式6解得。式7可采用FISTA[5]算法求解得到L值。
1.2.2S子问题求解
与L子问题类似,求解未知量S时假设L为固定值,求解公式如下:
(8)
同样的,令zr=GφS,上式更新为:
(9)
(1)未知量zr可通过分组软阈值法得到,令rri=(GφS)gi,求解公式为:
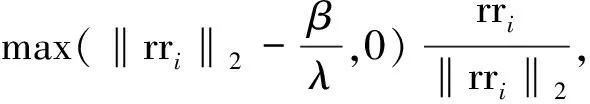
i=1,2,…,s
(10)
(2)未知量S求解公式如下:
(11)
上式亦可采用FISTA方法求解。
1.2.3 重建算法总结
针对目标函数,利用交替最小化将函数分为两个子问题求解,结合上述重建步骤构建算法DualWaTMRI,该算法重建步骤总结如下:
输入:最大迭代次数N,k空间测量值b,阈值比μ。
步骤1:初始化。
步骤1.1:对b进行傅里叶逆变换预处理,生成初始图像x0;
步骤1.2:对x0取合适的阈值μ互补分解得到初始残差分量S0;
步骤1.3:令初始平滑分量L0=0,n为迭代次数,初始化n=1,ρ=1/Lf。
步骤2:交替最小化求解。
步骤2.1:求解L子问题:给定Sn-1,结合Ln-1求解式5得到zp值,将zp值代入式7求解Ln;
步骤2.2:求解S子问题:给定Ln,结合Sn-1求解式10得到zr值,将zr值代入式11求解Sn;
步骤2.3:令n=n+1,判断n是否等于N,若不等于,回到步骤2.1,否则跳到步骤2.4;
步骤2.4:重建图像是平滑分量和残差分量的叠加:x=L+S(此时L=Ln,S=Sn)。
2 实验结果与分析
对Chest,Heart,Brain和Shoulder等四幅标准MRI图像进行实验。将DualWaTMRI与CG[4]、TVCMRI[6]、FCSA[8]和WaTMRI[15]算法进行比较。根据经验设α=0.02,β=3.5e-2,λ=β/2,Lf=1。同时选小波为稀疏基,伪高斯[6]为采样模板,测量矩阵为采样模板下的部分傅里叶矩阵。结果如表1所示。
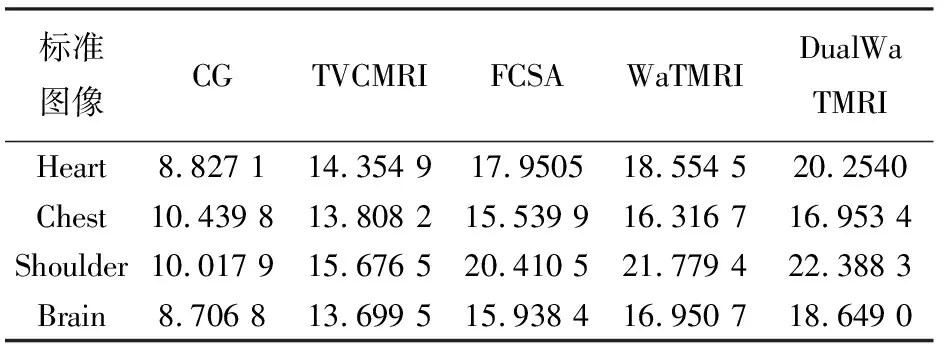
表1 四幅MR图像进行重建时的PSNR结果 dB
2.1 实验参数:阈值比μ的选取
对DualWaTMRI算法进行仿真,阈值比μ取值从0到1,结果如图2所示。
从图2可看出,在μ取值为0.05~0.20时,SNR值急剧上升,在μ大于0.20时,SNR值稍有减少,最后趋于平缓。可以得出,在DualWaTMRI算法互补分解模型中μ取值0.16。
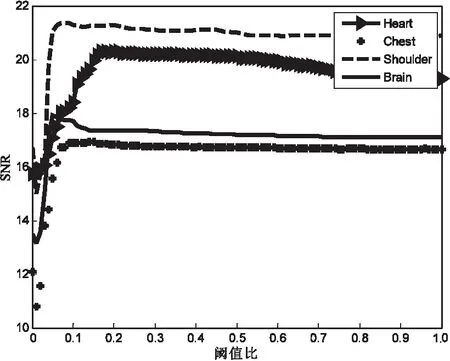
图2 仿真结果对比
2.2 重构性能的比较
将MR图像分别通过CG、TVCMRI、FCSA、WaTMRI和DualWaTMRI等算法进行仿真,结果分别如图3、4和表1所示。
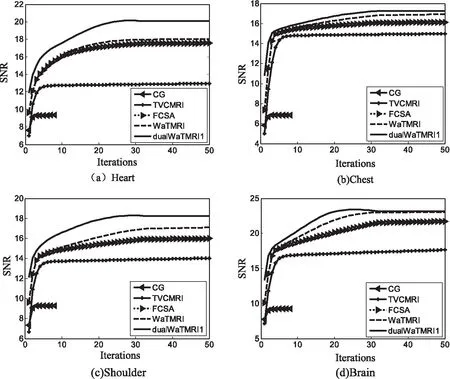
图3 四幅MR图像的SNR比较
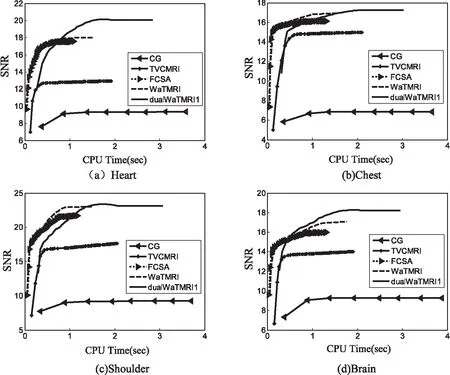
图4 四幅MR图像的t比较
图3和图4给出了四幅MR图像通过不同算法得到的仿真结果折线图(SNR和t)。表1给出了SNR具体值。从图3和表1中可以看出,四幅MR图像通过DualWaTMRI算法得到的信噪比最高,比WaTMRI算法分别高出约1.69 dB、0.63 dB、0.60 dB和1.70 dB,更优于其他算法。但图4中DualWaTMRI算法上升趋势最慢,表明重建时间长,这是由于目标函数中有两个未知量,需要交替求解,因此文中算法通过牺牲少量计算时间,达到增加信噪比的目的。
综上,DualWaTMRI算法与同类CS-MRI算法相比,虽然由于先验信息丰富导致图像的重建时间有所增加,但重建图像的质量有一定改善。
3 结束语
为改善TV造成的图像细节模糊问题,引入互补分解模型,与小波树结构稀疏相结合,提出一种基于小波树和互补分解的CS-MRI重建算法。利用互补分解模型将MR图像分为平滑和残差两个分量,仅将平滑分量用于TV,残差分量用于1范数,利用两个分量各自的特性,很好地保留了图像的细节信息,同时利用树结构稀疏特性,丰富图像的先验信息,使得在同等数目的扫描数据下,能得到更好的重建图像,或者只需更少的扫描数据,就能获得同等质量的重建图像。实验结果表明,与现有的基于整幅图像全变分、基于小波树的算法相比,该算法以部分运算时间为代价很好地改善了MR图像的重建质量。

