基于多分辨率和自适应分数阶的Active Demons算法
张桂梅 郭黎娟 熊邦书 储 珺
1(南昌航空大学计算机视觉研究所 南昌 330063) 2(南昌航空大学信息工程学院 南昌 330063)
数字图像配准[1]是指在不同时段、不同视角和不同传感器下拍摄的2幅或者多幅图像间的几何变换关系的处理技术.图像配准技术广泛应用于环境监测、物体或者场景识别、医学影像分析等与人类息息相关的各个方面.根据待配准目标的类型可以将图像配准分为刚性配准和非刚性配准.刚性配准方法适用于刚性目标或者不存在变形的图像配准,但在自然场景中目标大多是非刚性的,所以需要采用非刚性图像配准方法来解决非刚性图像配准问题.非刚性图像配准方法主要可以分为基于空间变换的配准方法和基于物理模型的配准方法两大类[2]:1)基于空间变换的非刚性配准方法,采用图像的空间变换来拟合图像的变形.常用方法有多项式法[3]、小波基函数[4]、B样条[5]等.2)基于物理模型的配准方法是将待配准图像到参考图像的形变过程视为一个物理变形,通过选择合适的物理模型来拟合这种形变以达到配准的目的.常用的模型有基于弹性力学理论的模型[6]、基于粘性流体的模型[7]以及基于光流场理论的模型[8-11].其中,基于光流场模型的非刚性配准方法由于其较高的检测精度和较好的稳健性得到越来越多的重视.Thirion[8]提出基于光流场理论的Demons算法,该算法的基本思想是利用参考图像梯度驱动浮动图像中的每一个像素向参考图像对应的像素点移动.但是该算法只采用了参考图像的梯度信息来驱动浮动图像发生形变,当梯度信息不足时容易产生误配准.He等人[9]根据作用力和反作用力原理对Demons算法进行改进,提出了允许参考图像和浮动图像的梯度共同驱动像素点向着对方对应的像素点移动的Active Demons配准算法.Vercauteren等人[10]为了保证形变场的拓扑性,提出了微分同胚Log Demons算法,其基本思想是将基于图像灰度的Demons算法的配准过程看成能量优化过程.Lorenzi等人[11]提出基于局部互相关相似性测度的微分同胚LCC Demons算法,该算法可以削弱灰度偏差对医学图像配准的影响,具有更高的配准精度.在临床实际应用中,准确、有效和鲁棒的图像配准可以避免医学图像中各种偏差引起的影响.由于存在的非刚性配准算法对严重扭曲变形的图像配准精度和效率都比较低,张桂梅等人[12]提出基于Nyström低阶近似和谱特征的图像非刚性配准算法,同时为了提高配准精度,在该模型中加入了小波变换的多分辨率策略.Tang等人[13]在Active Demons中引入平衡系数,将与弹性系数共同调节驱动力的强度,在引入平衡系数的同时加入了多分辨率策略,既提高了配准精度,也提高了收敛速度.但是以上这些方法的驱动力都只是来源于图像的灰度信息,这对于灰度均匀、弱边缘和弱纹理的图像配准优化容易陷入局部最小,从而降低配准的精度.
分数阶微积分是整数阶微积分的推广,它不仅拓宽了阶次的运算范围、丰富了微积分理论,而且比整数阶微积分更灵活.在图像处理领域,微积分理论已经取得了初步的应用.如Pu等人[14]和Chen等人[15]针对传统的整数阶微分去噪方法很容易导致边缘和纹理细节模糊,提出了将分数阶微积分理论运用于图像去噪,实验结果表明,基于分数阶的图像去噪算法提高了图像的信噪比,而且对纹理的保持效果也有所提升.张桂梅等人[16]针对原始和各种扩展的Demons算法对灰度均匀和弱纹理区域无效的问题,将R-L分数阶梯度应用到Demons算法中,该算法验证了R-L分数阶微分能够增强图像灰度变化较大的梯度信息,提高了配准精度和配准速度.但是分数阶主动Demons算法寻求图像配准效果最佳的阶次时,通常需要多次实验人工选取,费时费力,缺乏阶次自适应.Li等人[17-18]根据整幅图像的动态梯度特征调整分数阶,用于图像的增强和去噪,实验证明了该模型的有效性.张桂梅等人[19]针对RSF活动轮廓模型在分割弱纹理、弱边缘图像时,优化易陷入局部极小导致曲线演化速度缓慢和局部拟合项的高斯核函数会导致目标的边界模糊的问题,提出了一种基于自适应分数阶的活动轮廓模型,实验表明,该方法的分割精度与分割效率都有较大的提高.
针对上述问题,本文在文献[16]的基础上做了一些新的工作:1)构建了自适应分数阶阶次的数学模型.由于文献[16]的最佳阶次需要通过多次实验人工选取,费时费力.本文根据图像的局部特征(图像梯度模值和信息熵),构建了自适应分数阶阶次的数学模型.该模型以反正切函数为原型,以图像的梯度模值和信息熵为自变量,建立了微分阶次与图像局部信息之间的关系,从而可以根据图像的局部信息特征自动计算图像中各个像素点的最佳阶次,并将该模型应用在Active Demons算法的图像配准中.2)为了提高配准的效率,引入了多分辨率策略.采用下采样将图像进行分层,先在最低分辨率层应用较少的时间进行粗配准,并将其配准结果作为更高分辨率层的初始参数,再在高分辨率下利用较多的时间来进行精配准;逐层细化,按照由粗到精的方式执行,从而提高图像配准精度和效率.
1 相关理论
1.1 Demons算法
为了补偿时序图像的2幅连续帧之间物体和视点的相对运动,光流的概念被引入到了计算机视觉中.Thirion[8]提出基于光流场理论的Demons非刚性配准算法,该算法的基本思想是将参考图像S和浮动图像M看成是连续运动的图像序列中的2帧,要完成图像配准的过程,即要找到1个驱动力F,利用驱动力驱动浮动图像中的每一个像素向参考图像对应的像素点移动.假设图像在运动过程中亮度保持恒定,根据光流场方程可以得到空间任意一点p(x,y)的形变向量u:

(1)

但是,当参考图像为灰度均匀图像时,参考图像的灰度梯度就可能为0,此时容易造成u很不稳定.基于此,在式(1)中添加1个外力,则有:
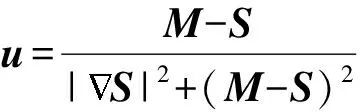
(2)
1.2 Active Demons算法
原始Demons算法只采用了参考图像的梯度信息来驱动浮动图像发生形变,但是当图像中灰度均匀、梯度信息不足时,易产生误配准,并且原始的Demons算法只适用于处理小形变图像,对大形变图像配准效果较差.于是,He等人[9]根据牛顿第三定律,同时用参考图像和浮动图像的梯度信息来驱动形变,其中浮动图像的梯度信息作为一种正内力,参考图像的信息作为一种负内力.于是就有:
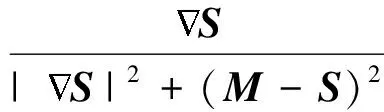
(3)
由于引入了正内力后,参考图像和浮动图像的梯度则共同驱动着对方对应的像素点移动,所以可以有效地配准大形变图像.为了方便调整驱动力强度,在式(3)上加入了均化系数β,于是有:
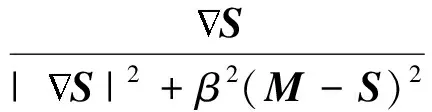
(4)
这样可以通过改变β的值控制形变向量的大小,选择合适的β值,既可以提高配准的精确度,也可以加快收敛速度.
1.3 分数阶的Active Demons算法
原始和各种扩展的Demons算法的驱动力都只是来源于图像的灰度信息,这对于灰度均匀、弱边缘和弱纹理的图像配准无效或者优化容易陷入极小.然而,分数阶微分既可以增强图像的纹理细节,又可以保留图像的平滑区域信息.所以,文献[16]将分数阶梯度代替了图像的梯度,于是有:
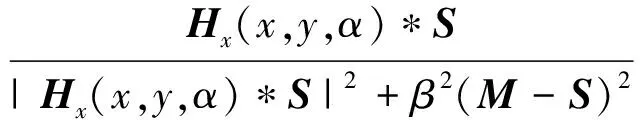
(5)
其中,Hx(x,y,α)和Hy(x,y,α)是二维图像x轴方向的分数阶微分掩模和y轴方向的分数阶微分掩模.
分数阶的Active Demons算法既提高了配准精度,也加快了图像配准的速度.
2 本文算法
2.1 分数阶微分对信号的作用
以连续函数整数阶的经典定义为基础,将微积分的阶次由整数扩展到分数.对于任意一个平方可积分的信号f(t)∈2,其傅里叶变换为
(6)
将整数阶信号扩展到分数阶,则有阶次为α的分数阶微积分形式:
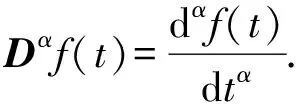
(7)
当α>0时,Dα表示α阶微分乘性算子;当α<0时,Dα表示α阶积分乘性算子.其傅里叶变换为
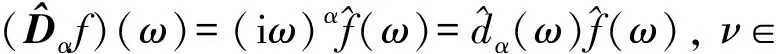
(8)
其中:
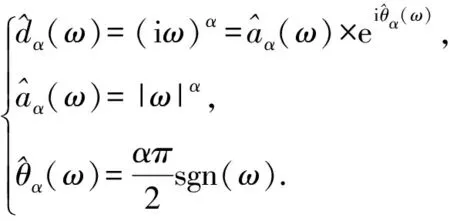
(9)
根据式(9)绘制分数阶微积分幅频曲线图,如图1所示.当α<0时,高频信号有极大的衰减;同时,低频信号有一定程度的增强.当0<α<1时,中高频信号得到了增强,其中中频信号得到了较大的增强,低频信号没有极大的衰减,而是进行了非线性的保留.当1<α<2时,高频信号得到了极大的增强,然而低频信号却得到了极大的衰减.在图像处理中,图像的平滑区域属于低频信号,图像的纹理细节属于中频信号,图像的边缘和噪声属于高频信号.本文的目的是要解决灰度均匀、弱边缘和弱纹理的图像配准问题,即既需要增强中频信号,又需要保留低频信号,同时结合幅频特性可知,本文的分数阶阶次宜选在0~1之间.分数阶阶次的选定将为自适应分数阶微分模型的构建提供理论基础.
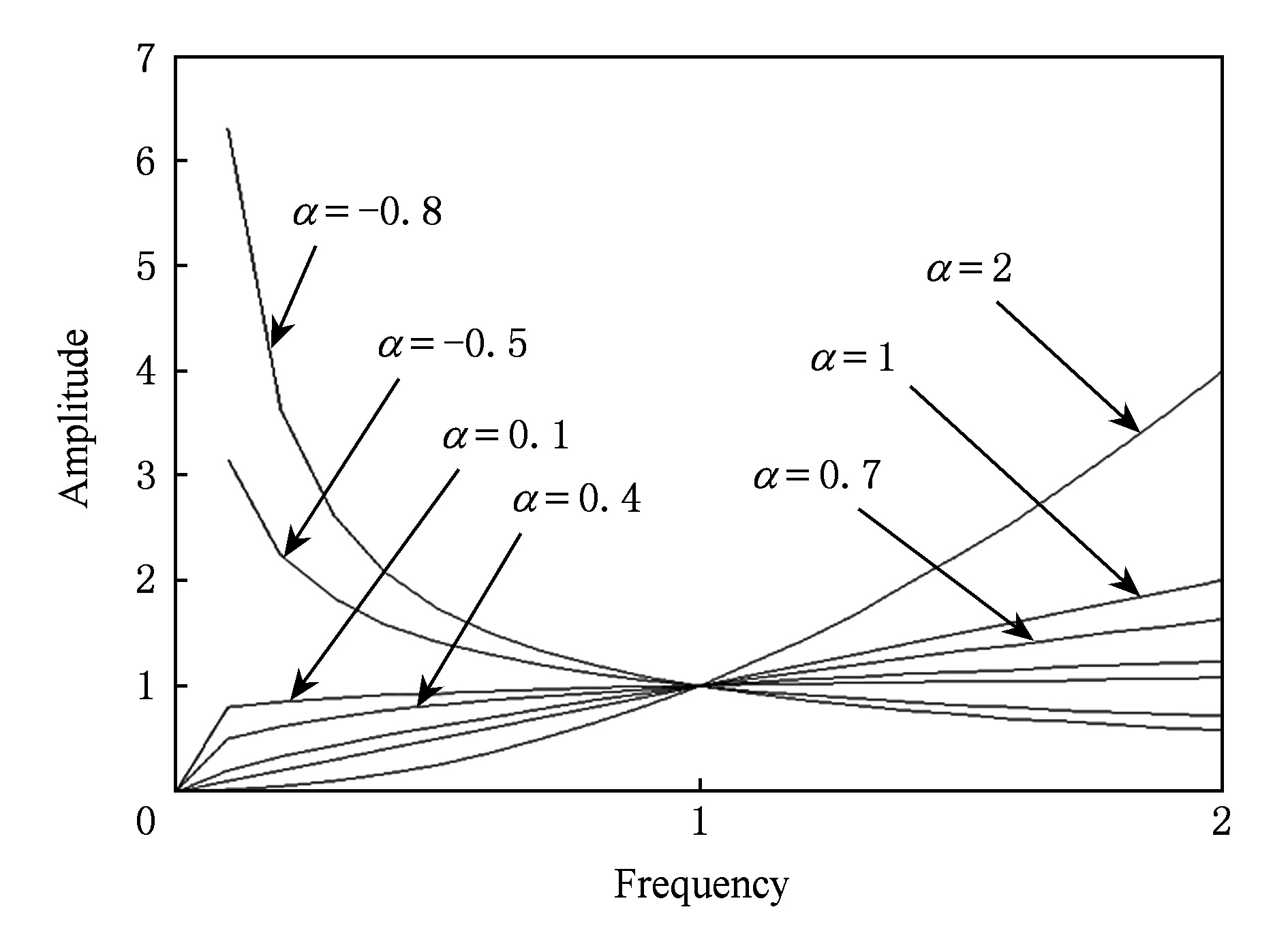
Fig. 1 The amplitude-frequency curve of fractional differentiator图1 幅频特性曲线图
2.2 构造R-L分数阶微分掩模
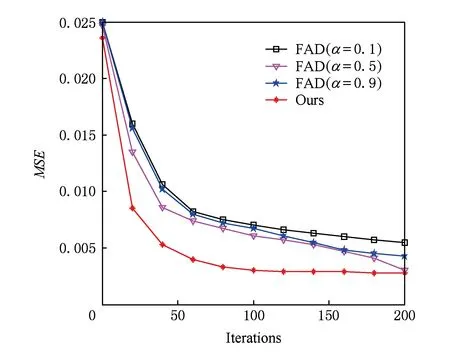
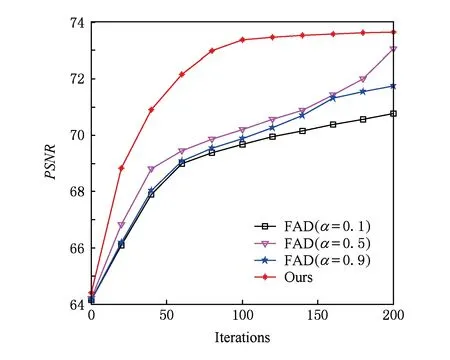
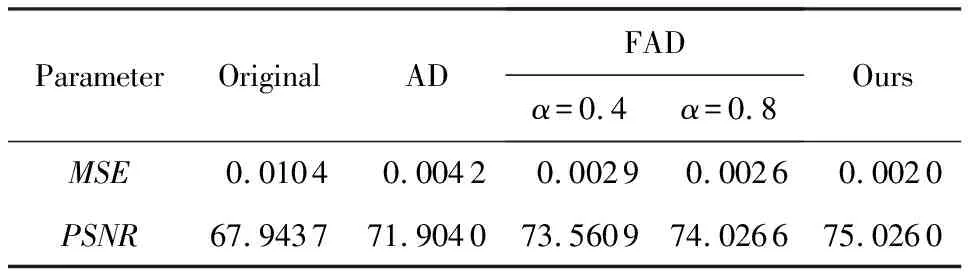
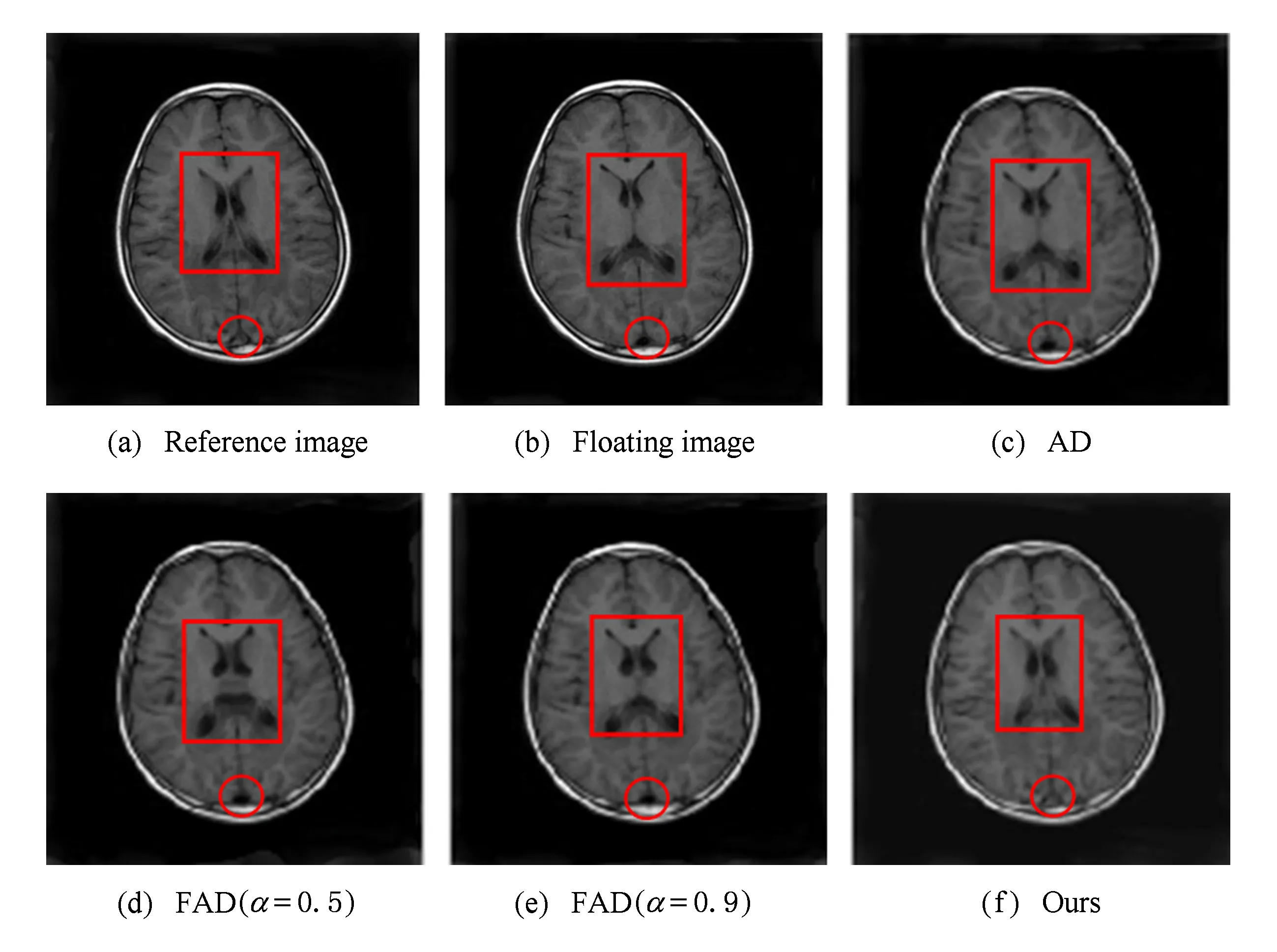
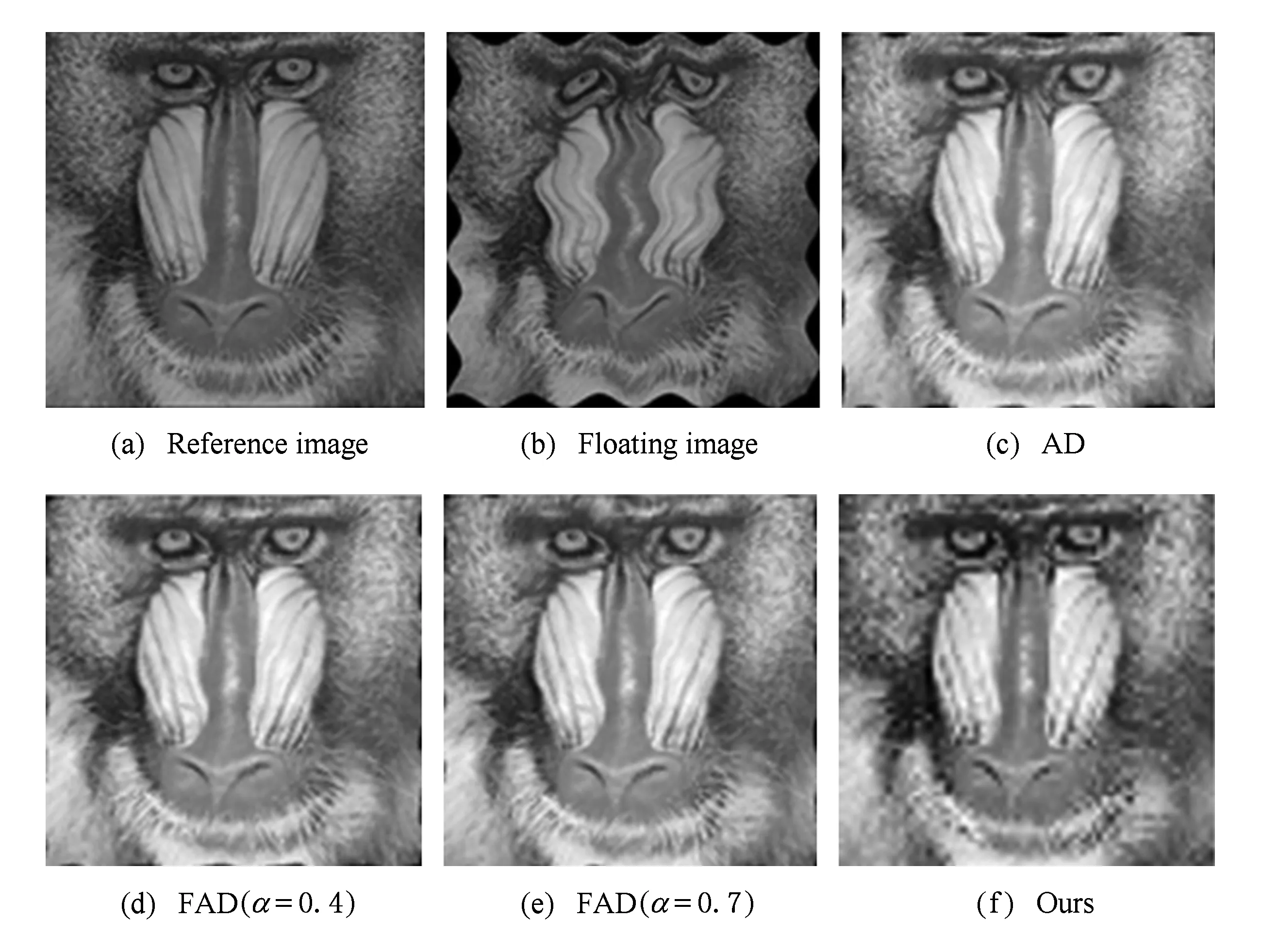
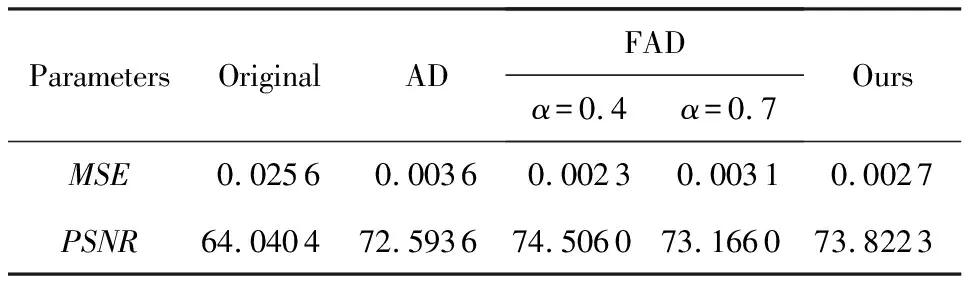
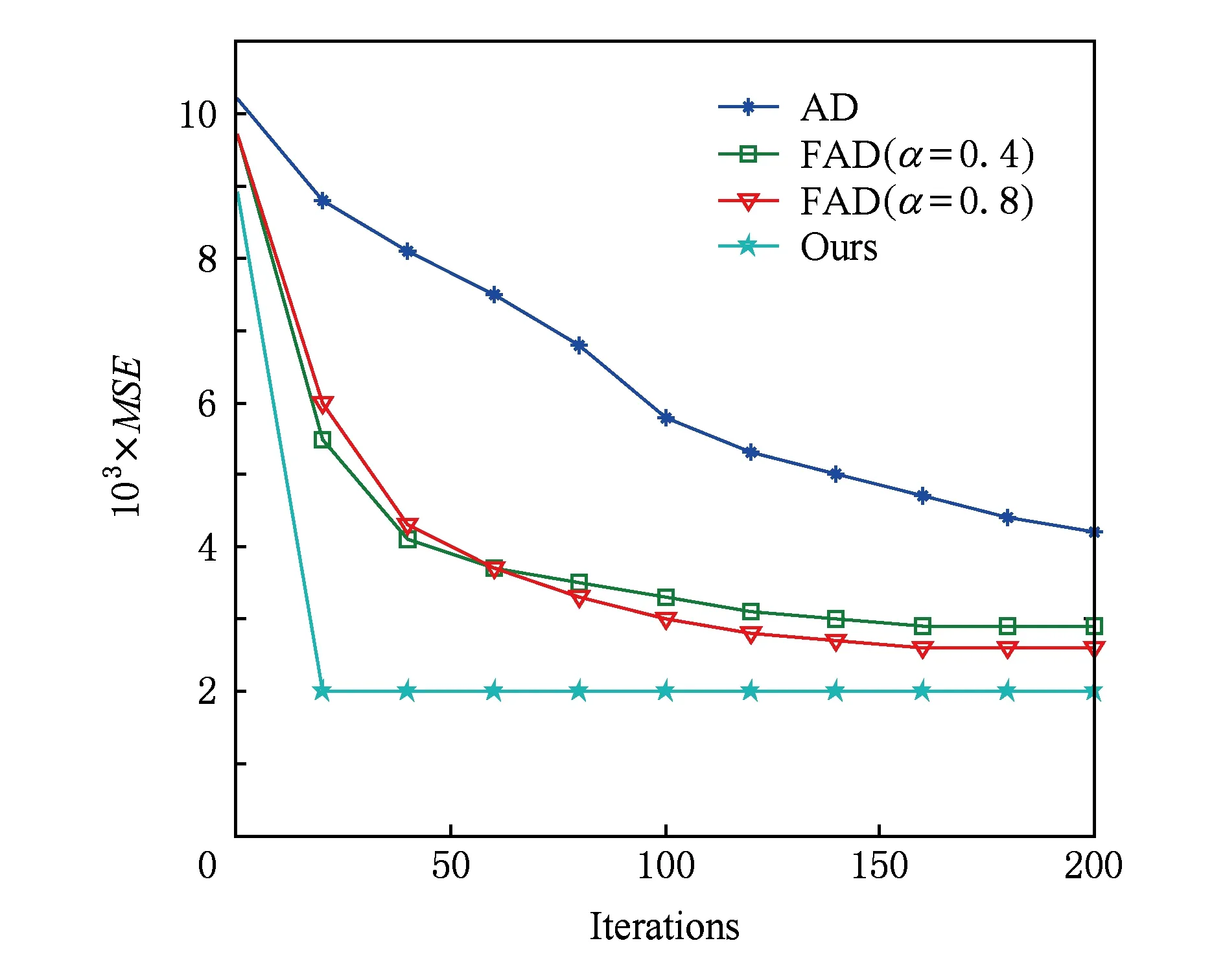
假设信号f(t)(t∈[a,b],a (10) 其中: (11) 将R-L分数阶微分进行一阶求导有: (12) 根据卷积定理,R-L分数阶微分定义可改写为 (13) 将R-L分数阶微分的卷积形式进行一阶求导,于是有: (14) (15) 对h(x,y,α)进行x和y方向一阶求导,则可以得到二维图像x轴方向的分数阶微分掩模Hx(x,y,α)和y轴方向的分数阶微分掩模Hy(x,y,α): (16) 实际上,图像是数值有限的数字量,而且图像灰度变化发生在最短距离的相邻像素之间,所以需要将Hx(x,y,α)和Hy(x,y,α)进行离散化: (17) 其中,xM=-K,-K+1,…,K-1,K,yM=-L,-L+1,…,L-1,L.Hx(x,y,α)和Hy(x,y,α)是(2K+1)×(2L+1)的微分掩模算子.将Hx(x,y,α),Hy(x,y,α)分别与图像进行卷积可以得到沿x轴和y轴方向的分数阶梯度,最终可以得到x轴和y轴方向的形变向量. 2.3.1 相关特性的选择 由于本文是要解决灰度均匀、弱边缘和弱纹理的图像配准问题,由图1可知,当选定阶次在0~1之间时,当分数阶阶次越小,低频信号的增强程度越大,也即低频信号的保留程度较大,所以在低频区域应该选取较小的分数阶阶次;当分数阶阶次越大,中高频信号的增强强度就越大,尤其是中频信号,所以在高频区域应该选取较大的分数阶阶次.由于一幅图像中通常都包含不同的频率段,所以在选择分数阶阶次时,不应该是整幅图像都选用同一个固定阶次,而是应该根据图像的相关特性选择不同的分数阶阶次.图像梯度和信息熵都可以反映图像纹理信息的丰富情况,所以本文根据图像梯度和图像信息熵构造自适应模型,以此实现自动为每个像素点都选取一个最佳的分数阶阶次. 在图像边缘和纹理区域,图像梯度较大;在图像平滑区域,图像梯度较小.图像f是一个二维离散函数,图像梯度是对这个二维函数在点(x,y)处进行求导,于是有: (18) 其中,I为图像的灰度,图像的梯度模值为 (19) 图像信息熵是信息量的一种度量方式,反映了图像纹理丰富情况.在图像边缘和纹理区域,图像信息熵较大;在图像平滑区域,图像信息熵较小.其定义为 (20) 其中,C为图像信息熵,(i,j)为像素坐标,Ii j为灰度值,ω为模板,Pi j为在模板内相同灰度值的概率. 2.3.2 构造自适应分数阶微分模型 在构造自适应分数阶函数时,为了保证分数阶阶次在0~1之间,将图像的梯度模值和信息熵进行归一化,即0≤|G|≤1,0≤|C|≤1.然后将归一化的图像梯度模值和信息熵进行融合,有: f(G,S)=m|G|+n|C|, 0≤f≤1, (21) 其中,m,n为权值,根据多次实验本文选取m=n=0.5. 由2.3.1节定义可知,当f值越大,对中高频区域的增强程度应该较大;当f值越小,那么对低频区域的保留程度应该较大.又由幅频特性可知,阶次在0~1之间,随着分数阶阶次的增大,中高频信号的增强强度越来越大,低频信号呈现非线性衰减;随着分数阶阶次的减小,中高频信号呈现急速衰减,然而低频信号却得到了有效的非线性的保留.所以,对于中高频区域,应该选取较大的分数阶阶次;对于低频区域,应该选取较小的分数阶阶次.也即f值越大,所选取的分数阶阶次应该较大;f值越小,所选取的分数阶阶次应该较小.为了保证分数阶阶次的选择在0~1之间,本文选用反正切函数为原型函数.自适应函数定义为 α=k×arctanf+b, (22) 其中,α为分数阶阶次;k,b为待定系数.由于f=1时,该像素点一定位于中高频区域,此时应该选取较大的分数阶阶次,即α=1;f=0时,该像素点一定位于低频区域,此时应该选取较小的分数阶阶次,即α=0.于是就有: (23) 所以自适应分数阶微分模型为 (24) 2.3.3 验证自适应分数阶微分模型的有效性 为了验证自适应分数阶微分模型的有效性,本节采用医学图像进行实验,如图2所示,其中图2(a)为参考图像,图2(b)为浮动图像.选用均方误差(MSE)和峰值信噪比(PSNR)评价配准的精度,MSE越小、PSNR越大,配准精度越高.将本文模型与分数阶Active Demons算法进行了比较,其实验结果如图3、图4和表1所示,其中图3和图4分别为均方误差(MSE)与迭代次数的关系曲线图、峰值信噪比(PSNR)与迭代次数的关系曲线图,实验中分数阶Active Demons算法的分数阶阶次选取3个效果较好阶次即0.1,0.5,0.9.从图3和图4的实验结果可以看出,自适应分数阶Active Demons算法的配准曲线收敛速度更快,并且均方误差和峰值信噪比在迭代100次的时候开始收敛,而分数阶Active Demons算法的均方误差和峰值信噪比在迭代200次时仍然没有收敛,即本文方法比分数阶Active Demons算法的效率更高.从表1中可以得出,自适应分数阶Active Demons算法的配准精度高于分数阶Active Demons算法.这是因为本文的模型是根据图像的局部特征自适应计算图像中每个像素点的最佳阶次,也即能确保在图像的每个像素点上都取到最佳阶次,且基于最佳阶次构造分数阶微分动态模板,阶次的选取更合理,所以配准精度和配准效率均能得到有效的提高. Fig. 2 Medical image图2 医学图像 Fig. 3 The relation curve between MSE and iteration number图3 均方误差与迭代次数的关系曲线图 Fig. 4 The relation curve between PSNR to noise ratio and iteration number图4 峰值信噪比与迭代次数的关系曲线图 Table 1 Comparison of Registration Accuracy BetweenTwo Algorithms 由于分数阶微分模板较整数阶的计算更复杂,并且本文得到微分模板是基于最佳阶次的动态模板,所以构造了自适应分数阶微分模型的配准时间相比于固定分数阶阶次的配准时间会有所增加.因此可以将多分辨率的分层配准策略应用到自适应分数阶Active Demons配准过程中,提高算法的运行速度和避免局部极值.配准按照由粗到精的方式运行,在低分辨率下利用较少的时间进行粗配准,在高分辨率下花销较多的时间进行精配准. 文献[13]提出了多分辨率策略的图像配准算法,下采样与小波变换相比,下采样能够提高信号的信噪比,它对信号进行隔点采样,将信息进行了压缩存储,从而提高了图像配准的速度和精度.本文考虑利用下采样将实验图像进行2层分解,先在最低分辨率图像上进行配准,然后将当层的配准结果作为更高一级分辨率图像配准的初始参数,直至配准到最高分辨率图像(原始图像). Fig. 5 Flow chart of our algorithm图5 本文算法流程图 算法1. 基于多分辨率和自适应分数阶的Active Demons算法. Step1. 输入参考图像和浮动图像; Step2. 用下采样将参考图像和浮动图像进行2层分解; Step3. 选取相同层的浮动图像和参考图像; Step4. 根据图像梯度模值和信息熵构建自适应分数阶微分模型α=4/π×arctanf; Step5. 根据式(24)计算每个像素点的最佳阶次,基于此,再根据式(17)计算每个像素点的R-L分数阶微分动态掩模; Step6. 根据式(5)求得形变向量u; Step7. 用高斯滤波器平滑配准后的变形场,主要是因为配准后的变形场不能满足平滑性要求; Step8. 判断是否到最后一层,如果不是,返回Step3,进入下一层图像配准;否则配准结束. 其算法步骤流程图如图5所示. Fig. 6 The result of Lena image registration图6 Lena图像配准结果图 本文实验所采用的计算机实验环境为:计算机配置为Pentium®Dual-Core CPU E6700 @3.20 GHz,内存2.00 GB,32 b的Widows 7.0版本操作系统,程序采用R2010a版Matlab实现.图像配准中常用的评价标准有客观评价和主观评价,其中主观评价就是我们用肉眼观察到配准后图像与参考图像的相似程度,客观评价就是用相似性度量来判断配准结果的好坏,常用的相似性度量有均方误差(MSE)、峰值信噪比(PSNR)、互相关系数(CC)、图像信息熵(C)等.本文主要采用主观评价、均方误差(MSE)和峰值信噪比(PSNR)来评价配准结果的好坏. 为验证本文算法的有效性,本文采用Lena图像、Brain图像和变形Baboon图像进行实验,由于本文算法是在分数阶Active Demons算法上进行改进的,所以将本文算法与分数阶Active Demons算法实验效果较好的2个固定阶次进行比较.又由于分数阶Active Demons算法是在Active Demons算法上改进的,所以也将本文算法与Active Demons算法进行比较. 3.2.1 Lena图像实验 本次实验采用图6(a)所示的Lena图像作为参考图像,图6(b)作为浮动图像,参考图像和浮动图像最大的差别就是Lena的脸部和帽子发生了变形.然后分别用本文算法、分数阶Active Demons算法和Active Demons算法进行实验,其实验结果如图6所示.其中图6(c)为Active Demons算法配准结果图,图6(d)和图6(e)分别为分数阶Active Demons算法在2个较佳阶次α分别为0.4和0.8的配准结果图,图6(f)为本文算法配准结果图.从图6可以看出,图6(c)的眉毛和帽檐的变形没有得到有效矫正,图6(d)和图6(e)的配准结果差不多,虽然帽子和眉毛处的配准很成功,但是图像最底部和头发部分出现了信息丢失现象.从图6(f)来看,其配准结果很理想,既矫正了变形,也没有出现信息丢失的情况.为了进一步验证本文算法的有效性,本文也进行了定量分析,实验结果如表2所示.从表2可以看出,本文算法的效果最好,这是因为本文首先根据图像的局部特征构造了自适应分数阶阶次的数学模型,使得在图像中每个像素点均能获得最佳阶次;其次引入了多分辨率的配准策略,即在低分辨率下进行了粗配准,将其得到的结果作为更高分辨率图像配准的输入,在高分辨率下进行精配准,所以本文的算法在图像配准的精度和效率都具有一定的优势. Table 2 Comparison of Registration Accuracy BetweenDifferent Algorithms 3.2.2 医学图像实验 本次实验采用图7(a)所示的Brain图像作为参考图像,图7(b)作为浮动图像,参考图像和浮动图像最大差别的地方就是中间部位和最底部(图7中矩形及圆圈标记处),参考图像最底部没有1个小黑点,而浮动图像最底部明显有1个小黑点.其中图7(c)为Active Demons算法配准结果图,图7(d)和图7(e)分别为分数阶Active Demons算法在2个较佳阶次α分别为0.5和0.9的配准结果图,图7(f)为本文算法配准结果图.从图7可以看出,图7(c)中间部位与浮动图像的中间部位差不多,并且配准图像的最底部与浮动图像一样还有1个小黑点,这并不接近参考图像;图7(d)中间黑色部位得到了加深,中上黑色部位有所扩大,中下部分那黑色的2点不再是连着的,比较接近参考图像,但是2个小黑点上方部位有一黑色横条,而参考图像中并没有这一黑色横条,而且配准图像的最底部也有1个小黑点;图7(e)中间部位相对于浮动图像来说,黑色部位有所扩大,但是还并没有接近参考图像,而且图像最底部仍然有1个小黑点;图7(f)中间黑色部位颜色就没有那么深,黑色部位形状也比较接近参考图像,中下部位也没有多出黑色横条,而且配准图像最底部没有了小黑点,所以本文算法配准的结果较好.为了进一步验证本文算法的有效性,本文比较了各种方法的均方误差(MSE)和峰值信噪比(PSNR),如表3所示.从表3可以看出,由本文算法配准后的图像,其均方误差和峰值信噪比都比较理想,这是因为本文算法在每个像素点上都获得了最佳的阶次,在图像的高频区域,选取了较大的分数阶阶次,在低频区域,选取了较小的分数阶阶次,故本文算法的配准效果比较理想. Fig. 7 The result of Brain image registration图7 Brain图像配准结果图 Table 3 Comparison of Registration Accuracy BetweenDifferent Algorithms 3.2.3 变形Baboon图像实验 本次实验采用纹理比较丰富的变形Baboon图像进行实验,其中图8(a)为参考图像,图8(b)为浮动图像,浮动图像相对于参考图像是Baboon图像大部分部位发生了变形,而且图像周围出现了波浪变形.分别用本文算法、分数阶Active Demons算法和Active Demons算法进行实验,其实验结果如图8所示.其中图8(c)为Active Demons算法配准结果图,图8(d)和图8(e)分别为分数阶Active Demons算法在2个较佳阶次α分别为0.4和0.7的配准结果图,图8(f)为本文算法配准结果图.从图8可以看出,图8(c)的中间部位基本不存在变形了,但是其周围的波浪变形还没有完全矫正,而且图像变亮;图8(d)基本上没有变形区域了,只是图像底部的波浪变形的矫正还有所欠缺;而图8(e)的配准结果相比前2个有所改善,所有的变形都得到了较有效的矫正;从图8(f)可知,图像得到了更好的矫正,但是图像变得稍微模糊,这主要是因为本文算法中加入了多分辨率配准策略,该策略会丢失某部分信息,所以图8(f)的结果会相对模糊.同理我们计算了各种算法配准结果的均方误差和峰值信噪比,其结果如表4所示. 从表4可以看出,本文算法的MSE和PSNR并不是最好的,但它与最好的结果相差不大,与未配准的MSE和PSNR相比,本文的MSE和PSNR还是得到了很大的提高.总之,本文算法的配准结果比较理想. Fig. 8 The result of Baboon image registration图8 Baboon图像配准结果图 Table 4 Comparison of Registration Accuracy BetweenDifferent Algorithms 3.2.4 配准效率实验 本文从收敛速度和配准时间2方面对配准的效率进行评价,分别使用了Lena图像、Brain图像和变形Baboon图像进行了实验.其中图9、图10和图11分别是Lena图像、Brain图像和变形Baboon图像的均方误差与迭代次数的曲线图,从曲线图可看出,本文算法的结果在迭代20次时就开始收敛,其他算法最少在迭代60次时才开始收敛,即本文算法的收敛速度是最快的. Fig. 9 Iterative curve of Lena image图9 Lena图像迭代曲线图 由于寻找分数阶Active Demons算法的最佳阶次比较费时费力,所以本文在此基础上构造了自适应分数阶微分模型.本部分将对分数阶Active Demons Fig. 10 Iterative curve of Brain image图10 Brain图像迭代曲线图 Fig. 11 Iterative curve of Baboon image图11 变形Baboon图像迭代曲线图 算法和本文算法的配准时间进行比较,本次实验图像仍然为Lena图像、Brain图像和变形Baboon图像.本实验的目的主要是测试本文算法在配准时间上是否具有优越性,其结果如表5所示.从表5可以看出,本文算法的配准时间是最多的,这是因为本文算法中加入了自适应分数阶微分模型,计算了图像中每个像素点的最佳阶次,随之构造了动态的R-L分数阶微分掩模;而基于分数阶的Active Demons算法人工选取了1个固定的分数阶阶次,整幅图像也只对应1个R-L分数阶微分模板;所以,本文算法的配准时间会比固定1个分数阶阶次的配准时间要更多.但是运用分数阶的Active Demons算法来寻找1个较好阶次的过程中,需要通过多次实验寻找最佳阶次,即每次都需要更换1个分数阶阶次重复进行实验.假设阶次从0.1~0.9需要做9次实验,这样加起来的总时间会比本文算法的配准时间多很多.综上所述,本文算法在配准时间上具有一定的优越性,且不需要通过多次实验不停地寻找最佳阶次,实现了分数阶阶次的最适应计算. Table 5 Time Comparison of Two Methods表5 2种算法的时间对比 s 将自适应R-L分数阶微分引入到图像配准中,能解决灰度均匀和弱纹理区域的图像配准.本文基于图像的梯度模值和信息熵,以反正切函数为原型,构造了自适应分数阶阶次的数学模型,自动自适应计算整幅图像中各个像素点的阶次,该方法可以根据图像中每个像素点的局部特征信息自适应调节算子模板系数,对每个像素点分别应用相应的模板进行处理,有效地解决人工寻求最佳分数阶阶次的费时费力问题;此外,将多分辨率策略引入到自适应分数阶Active Demons算法中,从而提高了图像配准的精度和效率.本文的方法可以用于灰度均匀和弱纹理区域的非刚性图像配准,并能提高配准的精度和效率,是Active Demons算法应用的重要延伸.不足之处是本文自适应数学模型的建立仅考虑了图像的梯度模值和信息熵,所以该模型并不是最优的模型.今后的研究工作将进一步优化自适应数学模型,提高计算速度,进而提高配准效率.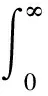

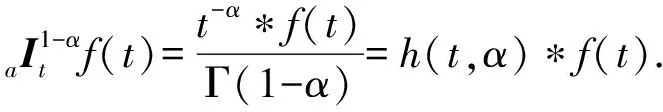
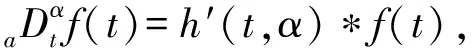
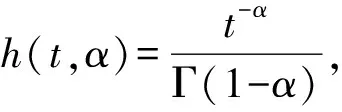

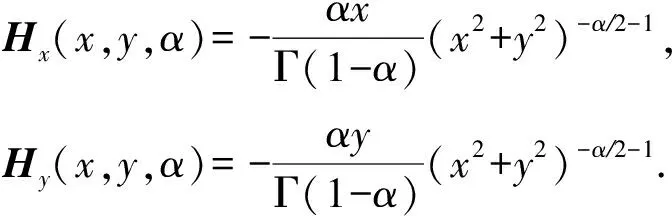

2.3 自适应分数阶微分模型的构造
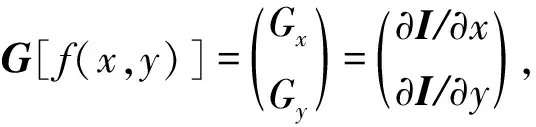
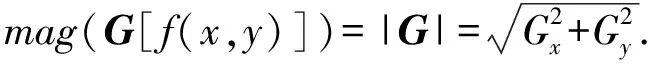

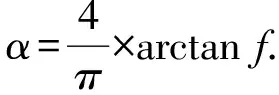


2.4 基于多分辨率策略的图像配准
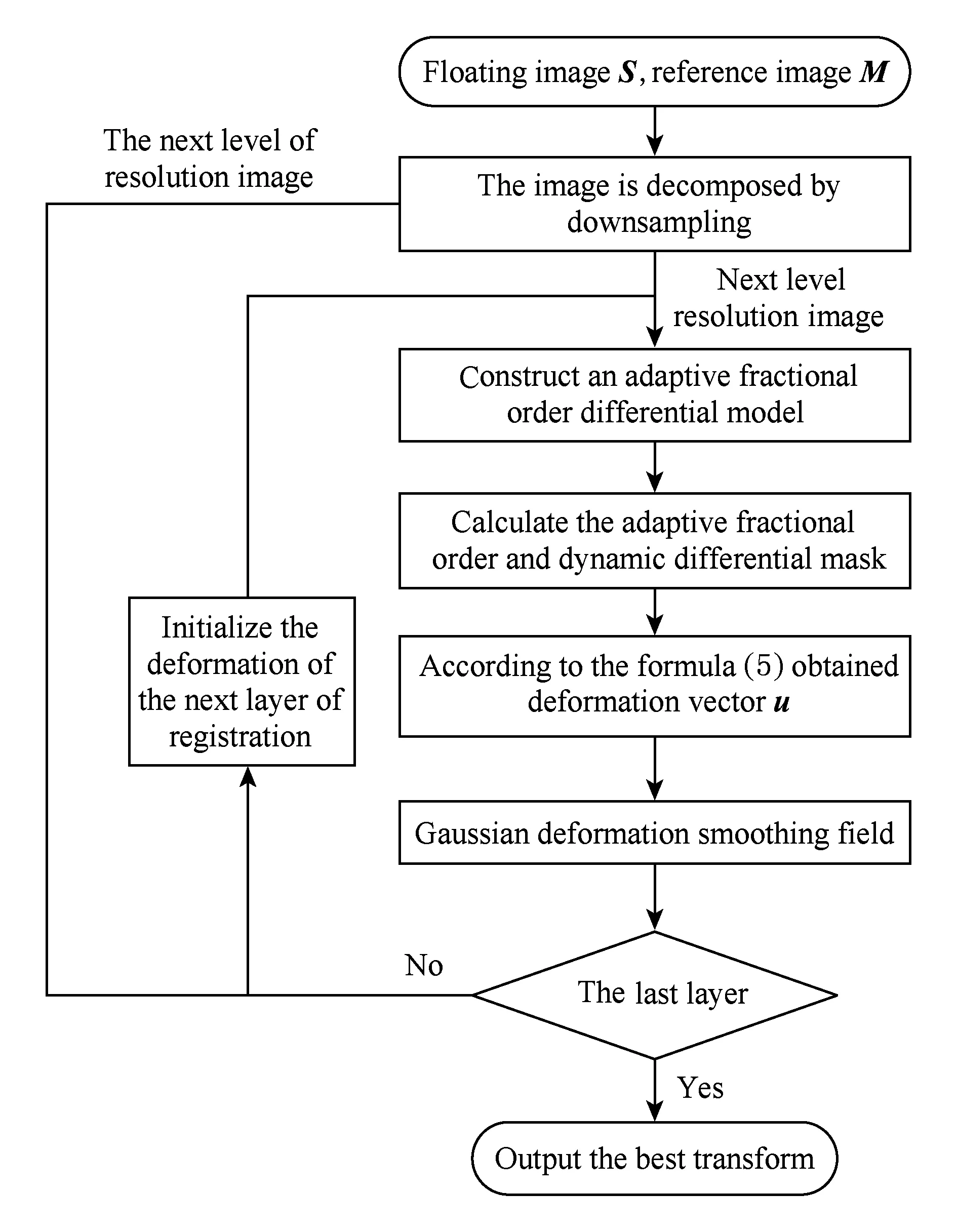
2.5 本文模型的配准算法步骤
3 仿真实验
3.1 实验环境和评价准则

3.2 实验结果和分析




4 结 论

