小波变换的动态灰色模型研究

张玉英，谭荣建，张东升，谢 玲



小波变换的动态灰色模型研究

张玉英1，谭荣建1，张东升2，谢 玲3

（1. 昆明理工大学 国土资源工程学院，云南 昆明 650093；2. 云南海钜地理信息技术有限公司， 云南 昆明 650000；3. 昆明市土地矿业权交易办公室，云南 昆明 650000）

利用小波变化的频带分离技术和消噪技术，可以获取真实的变形量。灰色理论模型可以解决信息缺乏的不确定性问题，但是无法优化含噪声、非平稳的信号，模型预测容易受到外界的误差干扰。本文研究将灰色模型与小波变换结合在一起进行数据预测，预测过程中加入动态信息，将灰色模型转换为动态灰色模型，提高预测精度。结合变形监测工程案例验证。结果显示，小波变换下的动态灰色模型，预测精度更高。

小波变换；灰色模型；噪声；动态灰色模型；变形监测

0 引言

随着科学技术和国民经济建设的快速发展，现代工程建设的速度与进度也随着加快，我们现在对建筑物的规模建设和精度都有更高的要求，为确保建设工程的安全，对工程建设中的变形监测环节显得尤为重要，特别是对数据的处理分析显得更加重要。自然界都普遍存在变形的现象，变形体变形在一定的范围内是允许的，如果超过允许值就有可能导致灾害的发生。变形监测的主要任务是是确定在各种外力作用和载荷下，变形体的位置、大小及形状的时间特征和空间特征。随着科学技术的发展和计算机水平的提升，各种方法和理论为变形预报和变形分析提供了广泛的研究途径。当前，变形体分析和模型理论方法发展成熟。当前，主要通过预报未来变形和分析变形原因来进行监测变形数据的处理，通过有线的数据要想预测变形体的变形情况有一定的难度。一般选择合适的数学模型，根据数据进行时序特征点进行预报。现在，常见的变形监测数据处理分析和预测处理模型有卡尔曼滤波模型、小波分析模型、动态灰色模型、时间序列分析模型、人工神经网络模型、频谱分析模型、回归分析法、小波变换、灰色分析模型等[1-2]，而利用一种模型进行预测不能达到很好的效果。然而每个模型有各自的优点和不足，由于变形监测是多因素形变因子的组合，在数据中含有多种因子，处理变形数据就涉及多个学科的融合交叉，要用的处理模型也是多样的，本文在查阅文献资料以及各种工程实例基础上,提出小波变换。因为小波变换具有时频局部变化和多分辨分析的特点，特别适用于对多种频率和非平稳序列的数据来进行去燥处理来提取其中的变形信息。利用小波变化可以很好的剔除建模数据的随机干扰噪声，抑制干扰信号，恢复有用信息，提高预测的精度[3-4]。GM(1，1)模型预测是一种常见的预测模型，该模型随着时间的推移，预测的精度不断降低。为了解决工程中面临的预测问题，预测中不断更新新的信息，构建动态的GM(1，1)模型。论文的创新点就是将小波变换与动态灰色模型结合进行预测，提高预报的精度。

1 灰色理论模型的建立

1.1 灰色GM(1,1)模型

构建GM(1,1)模型分为以下几个步骤[5-8]：

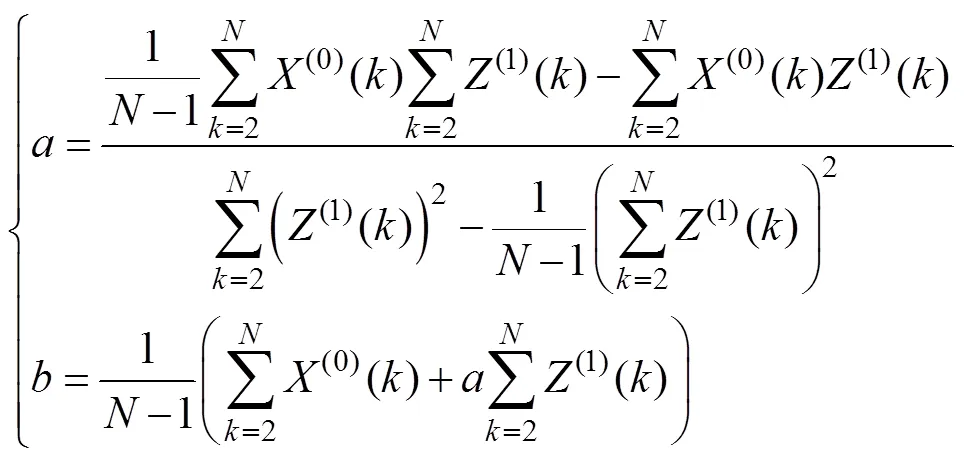
1.2 动态灰色预测模型的构建

1.3 GM(1,1)模型精度[9]

步骤如下：

①模型残差：

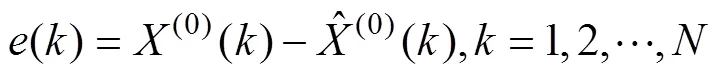
模型的好坏可以分为四个等级[10-12]，如下表1所示：

表1 GM(1,1)模型精度检验

Tab.1 Verification of GM(1,1) model precision

2 小波变换原理

小波变换（wavelet transform，WT）是一种新的变换分析方法，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征，能对时间（空间）频率的局部化分析，通过伸缩平移运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。

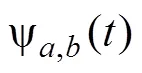
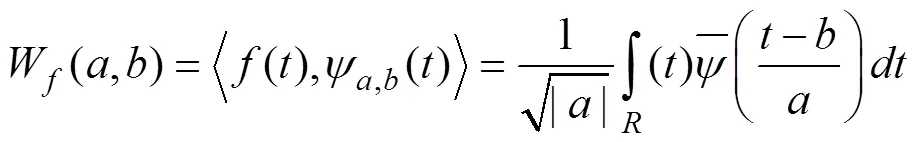
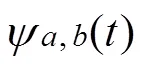
变形趋势信号体现在小波分解的低频层，而细节部分信号和噪声信号主要在小波分解出的高频层中体现。因此，对高频层进行门限阈值处理，减少高层的噪声量，再通过小波重构对低频层和进行过门限阈值处理的高频词进行重构，得到降噪后的信号[14]。变形监测数据的降噪由3个步骤组成：

（1）对变形监测数据进行N层小波分解；

（2）高频系数的阈值选择和门限阈值处理；

（3）小波重构。

3 工程实例比较

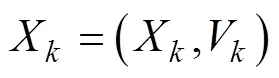
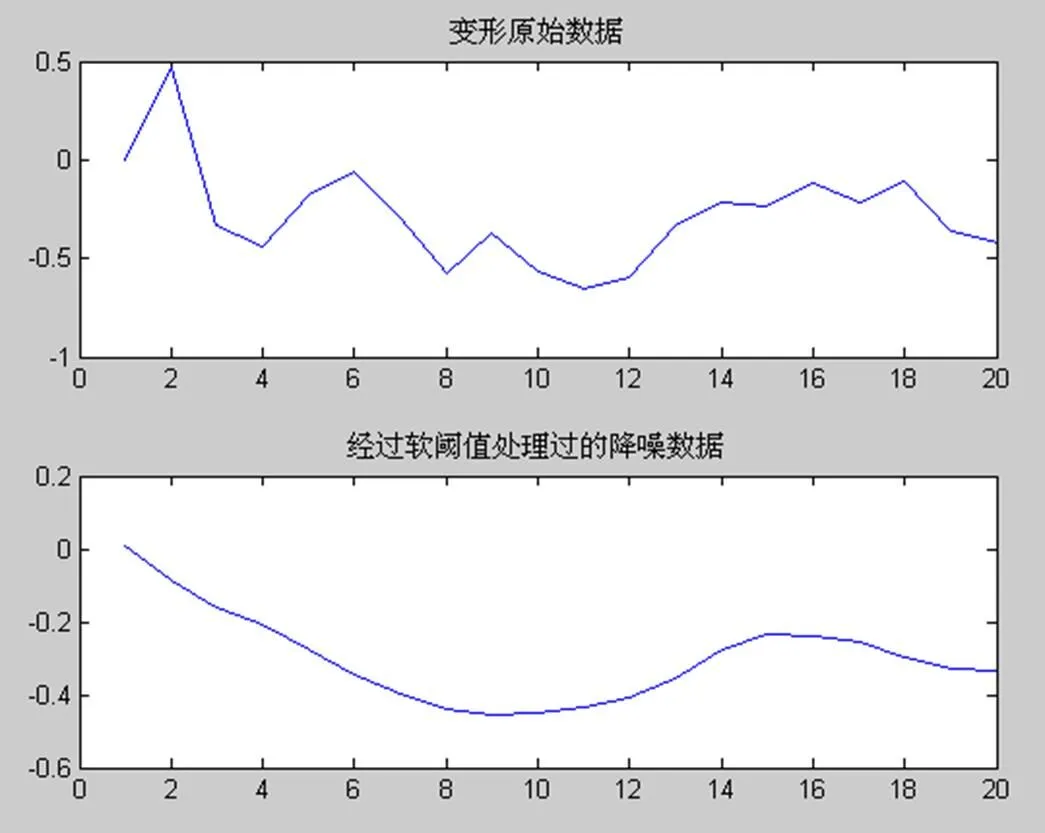
纵坐标：小波变化尺度（mm） 横坐标：时间尺度

图1可以看出，曲线经过软阈值处理之后变得比较光滑。根据选定的滤波初值及小波推导公式，对P4点20期的数据进行滤波处理，滤波结果见表1。

表2 小波变换

Tab.2 The wavelet transform

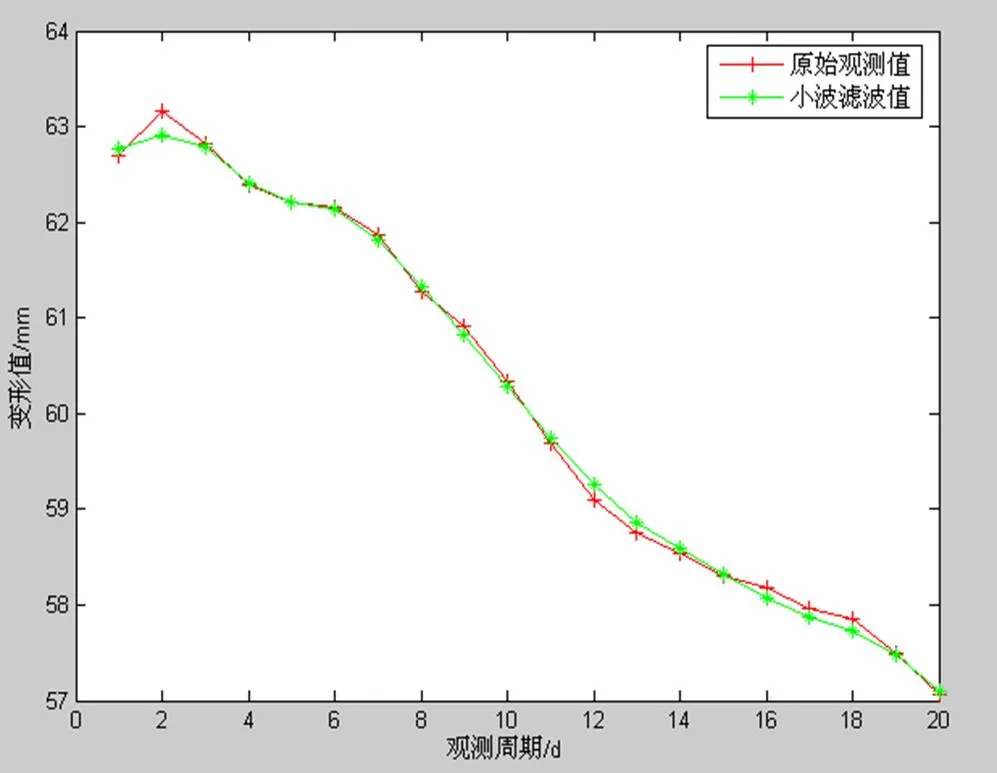
图2 原始数据与小波滤波后数据对比

图2可以看出来，消噪后剔除了噪声的影响，数据变得更加平滑，更能看出变形的趋势。

选取小波滤波值的前五个周期作为初始值，采用GM（1,1）模型进行预测。C=0.0709,小误差概率p=100%。预测6-20期的数值，结果如表3所示。

利用新的方法，将小波变换和动态灰色模型进行结合预测，预测结果如表4所示。

由图3可以看出，动态灰色模型的预测值与观测值的变化趋势一致，传统GM(1,1)模型预测值随时间增加偏离较大。传统GM(1，1)模型在预测中只修正了随机干扰误差，无法排除其它误差的影响。动态灰色模型，在预测过程中不断引入新的信息来进行修正，所以预测结果较为精确。

4 结论

小波变换可以将原始信号分解为频带不同的信号，在变形监测数据降噪中是一种有效的手段。通过小波变换对仿真数据进行去噪处理及进行特征信息提取，利用小波滤波后的数据，结合动态灰色模型进行预测，更能真实反映变形趋势，所以小波变换在变形监测数据处理中是一种有效的，具有优势的技术手段，得到了满意的结果。

表3 传统GM(1,1)模型预测

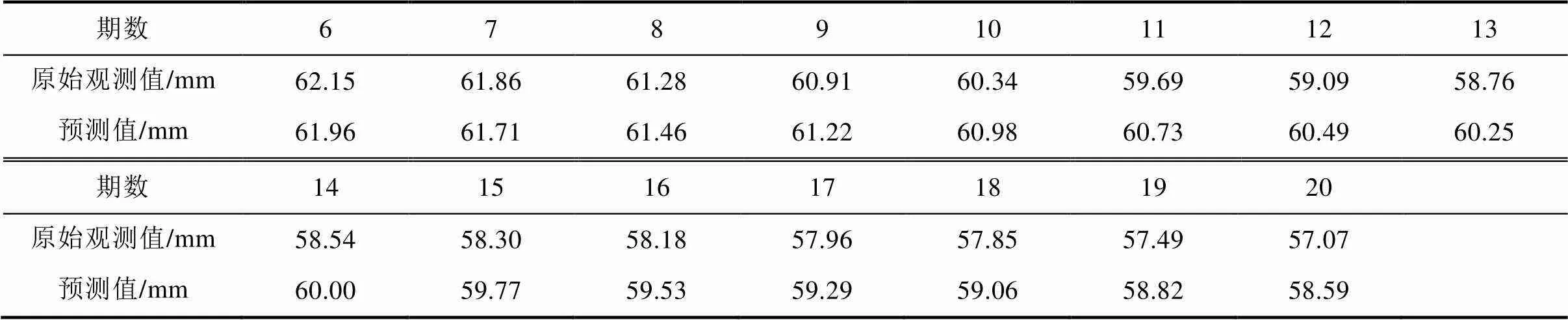
Tab.3 Traditional GM (1, 1) model prediction

表4 动态GM(1,1)模型预测

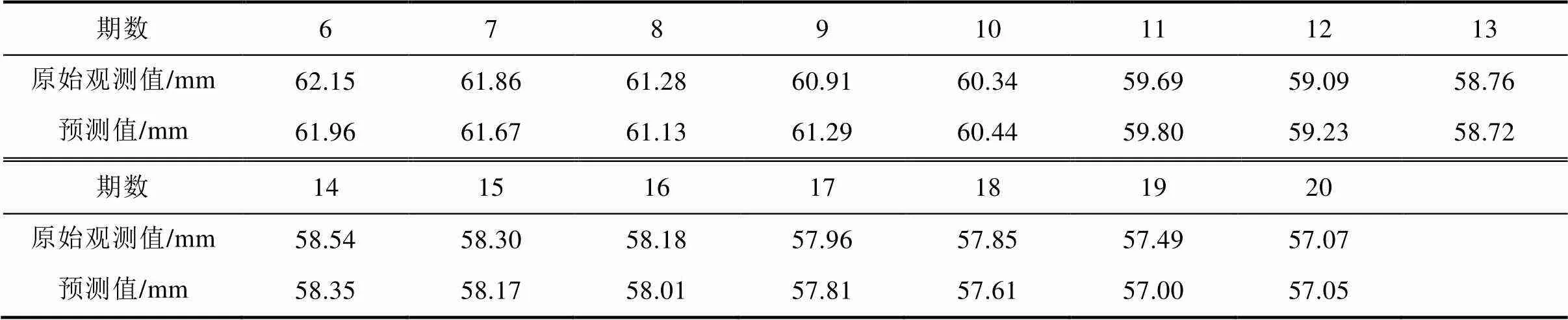
Tab.4 Dynamic GM(1,1) model prediction

图3 预测结果对比

[1] 王利. 公路边坡监测理论与GPS一机多天线系统研究[D]. 西安: 长安大学, 2006.

[2] 容静, 文鸿雁, 周吕. 一种改进灰色预测模型在变形预测中的应用[J]. 测绘科学, 2017, 42(3): 35-38.

[3] 黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉大学出版社, 2012.

[4] 焦明连, 蒋延臣. 基于小波分析的灰色预测模型在大坝安全监测中的应用[J]. 大地测量与地球动力学, 2009, 29(2): 115-117.

[5] 邓聚龙. 灰色系统基本方法[M]. 武汉: 华中理工大学出版社, 1987.

[6] 何君, 杨国东. 灰色预测理论在建筑物沉降中的应用研究[J]. 测绘通报, 2012(3): 63-64.

[7] 张健雄, 蒋金豹, 张建霞. 高层建筑沉降监测与灰色预测[J]. 测绘科学, 2007, 32(4): 56-59.

[8] 周吕, 文鸿雁, 韩亚坤. 灰色预测与Kalman滤波在建筑物沉降变形分析中的应用[J]. 测绘科学, 2014, 39(4): 149-152.

[9] 邓聚龙. 灰色系统论文集[M]. 武汉: 华中理工大学出版社, 1989.

[10] 李日云, 王利, 张双成. 灰色预测模型在高层建筑物沉降预测中的应用研究[J] . 地球科学与环境学报, 2005, 27(1): 84-87.

[11] 岳仁宾, 滕德贵, 欧斌, 肖兴国. 小波变换与GM模型在基坑监测中的应用[J]. 工程勘察, 2015(5): 68-72.

[12] 徐秀杰, 黄张裕, 凌晨阳, 张晖. 基于小波分析的灰色组合模型在变形监测数据处理中的应用[J]. 工程勘察, 2015(4): 80-83.

[13] 张勤, 蒋廷臣, 王秀萍. 小波变换在变形监测中的应用研究[J]. 测绘工程, 2005, 14(1): 810-815.

[14] 尹健华, 廖继旺, 刘云芳. 基于小波变换的噪声消除算法研究[J]. 测控技术, 2007, 15(36): 144-145

Research on Dynamic Grey Model of Wavelet Transform

ZHANG Yu-ying1,TAN Rong-jian1, ZHANG Dong-sheng2, XIE Ling3

(1. Faculty of Land Resource Engineering, Kunming University of Science and Technology, Yunnan Kunming 650093; 2. HI-GIS Geographic Information Technology Co.ltd Yunnan Kunming 650000; 3. Kunming Land Mining right Trading Office, Yunnan Kunming 650000)

Using the wavelet transform of the frequency band separation technology and denoising technology, we can get the real deformation. The grey theory model can solve the problem of the lack of information, but it can not optimize the signal with noise and non-stationary. In this paper, the grey model and wavelet transform are combined to predict the data, and the dynamic information is added into the forecasting process. Case study of deformation monitoring. The results show that the dynamic gray model is more accurate than the wavelet transform.

Wavelet transform; Grey model; Noise; Dynamic grey model; Deformation monitoring

P208

A

10.3969/j.issn.1003-6970.2018.11.035

张玉英(1988-)，女，硕士研究生，主要研究方向为变形监测、GNSS卫星导航定位理论与应用、地理信息技术与开发应用、测量数据处理与质量控制研究；谭荣建，男，副教授，硕士生导师，长期从事普通测量学、控制测量学、土地开发整理项目规划设计、数字化测量与成图等课程的理论与实践性教学、指导土地资源管理及测绘工程专业的毕业设计工作，现主要从事测绘及土地资源管理方面的学习与研究；张东升，男，硕士研究生，主要从事变形监测、测量数据处理与质量控制研究、工程测量新技术应用研究、GIS软件开发及应用研究；谢玲，女，大学本科，主要从事地籍测绘、土地科学、RS和GIS空间分析工作。

张玉英，谭荣建，张东升，等. 小波变换的动态灰色模型研究[J]. 软件，2018，39（11）：165-169