利用信道状态信息的室内定位技术

(北京信息科技大学 信息与通信工程学院，北京 100101)

1 引 言

随着对卫星定位和导航技术研究的不断深入，基于位置的服务(Location Based Servise,LBS)已经得到了很大的发展，其中应用最广泛的当属全球定位系统(Global Positioning System,GPS)[1]。随着社会城市化的发展，人类的大多数活动都发生在室内，室内的LBS需求渐渐得到重视。由于室内环境对卫星信号的遮挡和干扰较为严重，GPS在室内的定位结果不尽如人意，因此，室内定位技术[2]已成为学术界和产业界的研发重点。目前，基于接收信号强度(Received Signal Strength Indication,RSSI)[3]的室内定位技术因其成本较低和易于推广而受到广泛关注，其中对基于RSSI的位置指纹室内定位技术[4]研究较多：在离线阶段，通过采集不同位置的RSSI值构建指纹数据库；在线阶段，将测得的数据输入指纹数据库进行解算，从而得到定位结果。然而，RSSI值易受到室内多经效应的影响，导致定位结果不稳定[5]。

众所周知，RSSI值是媒介访问控制层(Media Access Control,MAC)的特性，而最新的研究已经转向对物理层(Physical Layer,PHY)的研究，信道状态信息[5](Channel State Information,CSI)就是典型的物理层特征值。CSI值的获取离不开正交频分复用(Orthogonal Frequency Division Model,OFDM)的应用。OFDM的主要思想是将信道分为若干个正交的子信道，使得数据由原来的高速传播转换成低速的并行传播，而CSI就代表了OFDM系统中每个子信道从发射端到接收端的信道状态，换言之，它代表了发射天线到接收天线的每一个子载波的信道矩阵，包含了每个子载波不同的幅度和相位信息，相比RSSI能更好地区分不同路径[6]。多路子载波同时发生波动的概率低于多径叠加值发生波动的概率，所以CSI信息相比RSSI更稳定。综上所述，CSI信息比RSSI能更精确定位。

现有的基于CSI值定位的方法主要有两种，一种是位置指纹法[7]，另一种为物理建模法[8]。位置指纹法主要通过采集不同位置的CSI值构建指纹数据库，并将实时测得的CSI值输入数据库进行解算并定位。虽然基于CSI的位置指纹法可以实现较高精度的定位，但其在离线阶段需要进行大量的数据采集，工作量和成本颇高。而且，一旦环境改变就必然需要更新指纹数据库，否则定位精度将受到极大影响。所以，位置指纹法并不适于大范围推广。而物理建模法则不需要大量的离线数据采集，可以实现在相对较低的成本下进行比较精确的定位。

本文利用物理建模法建立了信号CSI值与距离的传输模型，测得不同位置信号的CSI值，并通过传输模型回归出目标与信号发射端的距离，再利用三边定位法计算得出目标的坐标，从而实现定位。

2 信道状态信息

2.1 CSI概述

室内的无线信号在传播过程中会被墙壁、地面和家具等阻碍而出现反射和衍射等情况，并形成多径传播。在OFDM系统中，多径传播的无线信号的频域模型可表示为

Y=HX+N。

(1)

式中：Y表示接收端的信号向量，X表示发射端的信号向量，H表示信道矩阵，N表示附加的高斯白噪声。则所有子载波的信道状态信息可以表示为

(2)

其中每一个子载波的信道状态信息表示为

csi=csiejsin∠csi。

(3)

式中：csi和∠csi分别表示了每一个子载波的幅度和相位。由公式可知，比起RSSI，CSI更细粒度化地表征了各个子载波从发射端到接收端的信道增益信息，所以更适于室内定位。

2.2 CSI的获取

以往要获取信道状态信息必须依靠专用设备，这使得CSI难以被推广研究。然而，随着无线局域网的发展，在IEEE 802.11a/g/n标准中，我们可以利用商业无线网卡和开源固件获取信道状态信息。使用配有INTEL WIFI LINK 5300网卡的笔记本电脑，在Ubuntu 12.04 LTS-Ubuntu 14.04 LTS的操作系统下，使用文献[9]的驱动程序便可收集到CSI数据，并以表1的形式呈现出来。

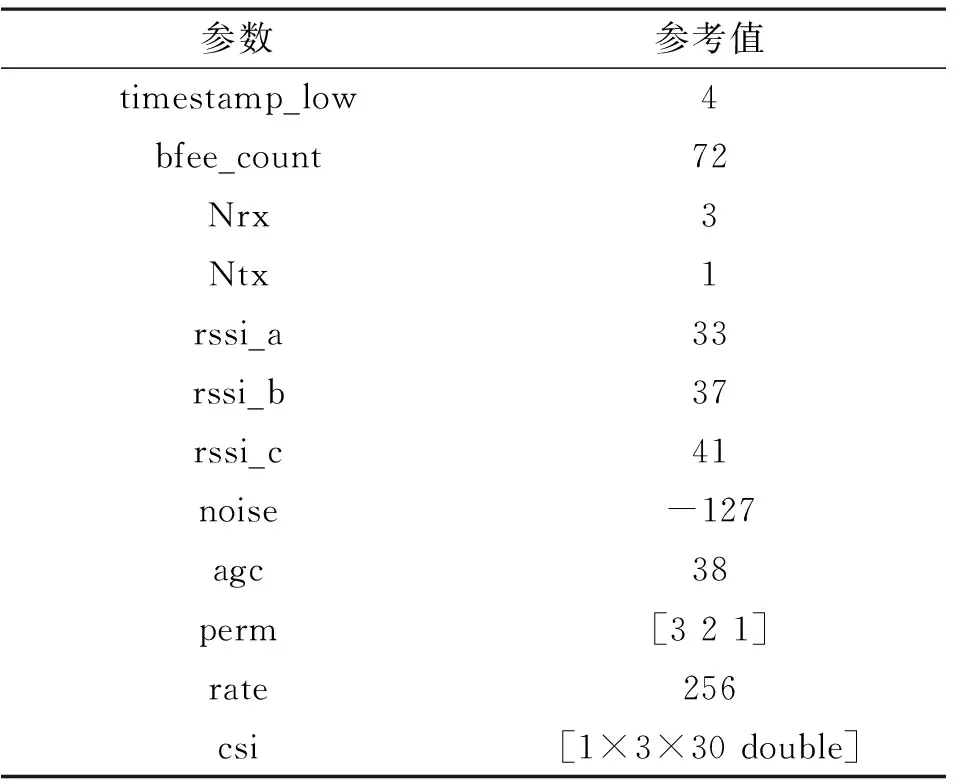
表1 一组CSI样本数据Tab.1 The CSI sample data

表1中，timestamp_low是无线网卡的低32位1 MHz时钟，在获取CSI的采样时没有被记录下来，所以所有的timestamp_low值均为4；bfee_count是驱动器发给用户空间的波束总数；Nrx代表了无线网卡的接收天线数量；Ntx代表了路由器的发射天线数量；rssi_a、rssi_b和rssi_c分别是无线网卡每个接收天线接收到的RSSI值；perm表示无线网卡如何将3个接收天线3个射频链路对应并处理数据；rate表示发射端发送数据包的速率；csi代表了信道状态信息，正是我们需要的CSI值，它是一个Ntx×Nrx×30的三维矩阵，第三个维度代表了OFDM的30个子载波。

3 定位原理与方案

基于CSI的室内定位总体结构图如图1所示。在离线阶段，获取与发射端AP不同距离的参考点的CSI值，并建立距离与CSI值的传输模型；在线阶段，采集目标位置接收端的CSI值，并对其数据进行处理，滤除干扰后，通过传输模型回归出AP到目标接收端的距离，再利用三边定位法并结合AP的坐标实现目标的定位。

图1 基于CSI的室内定位结构图Fig.1 The flow chart of indoor positioning based on CSI

3.1 CSI有效值和已有的距离传输模型

信道状态信息代表了30个子载波的幅度、相位以及衰落信息。将每个子载波的CSI值融合起来，可以降低衰落产生的误差，从而更精确地定位。文献[10]提出的FILA(Fine-grained Indoor Localization)系统将30个子载波的CSI值进行了加权平均，得到了CSI的有效值:

(4)

式中：f0表示信道的中心频率，fk表示第k个子载波的频率，Ak表示第k个子载波CSI的幅度，CSIeff表示CSI的有效值。除此之外，FILA系统通过改进自由空间传播模型，建立了CSIeff与传输距离的关系模型:

(5)

式中：c表示光速，σ是环境因子，n是路径衰减指数，两个参数都与室内环境有关。

然而，自由空间传播模型是指波在理想的介质中传播，其并不适用于复杂的室内环境，所以由自由空间传播模型改进得到的公式(5)误差较大，导致最后的定位精度不尽人意。本文对室内环境引入对数距离路径损耗模型(Log-Distance Path Loss Model,L-DPLM)[11]，在其基础上改进得到CSIeff与距离的对应关系。

3.2 对数距离路径损耗模型(L-DPLM)

室内的信号在传播过程中会受到障碍物的影响而发生反射、绕射和散射，并受到多径传播与非视距因素的干扰，因此在接收机处收到的信号强度为多个信号的累加之和[12-14]。大量的实验研究发现，在室内环境中，接收信号强度与传输距离呈对数关系，即

(6)

其一般表达式为

(7)

公式(7)即为适用于室内环境的对数距离路径损耗模型(L-DPLM)，其中，p(d)是接收端的信号强度，p(d0)是在距离发射端d0处的信号强度，两者的单位均为dBm，d0为参考距离，d为接收端到发射端的距离，γ为与环境相关的损耗因子，Xσ是反映信号衰减的随机因子，其单位为dB，服从正态分布。表2例举了典型环境的γ与Xσ值[15]。

表2 典型环境的γ与Xσ值Tab.2 The γ and Xσ of typical environments

相比自由空间传播模型，对数距离路径损耗模型添加了环境损耗因子γ与随机衰减因子Xσ，在一定程度上解决了室内多径效应和非视距因素的干扰问题，弥补了自由空间传播模型的不足。因此，由对数距离路径损耗模型改进得到新的距离传输模型，理论上应该比公式(5)(由自由空间传播模型改进得出)更适用于室内定位。

3.3 由L-DPLM改进得到的距离传输模型

对于公式(7)，取参考距离为1 m，且1 m处的信号衰减为A，发射端的信号强度为Pt，接收端的信号强度为Pr，则公式(7)可化为

Pr=Pt+A+10γlg(d)+Xσ。

(8)

因为Pt、Pr、A以及Xσ均已被对数化，两边去对数化得

(9)

即

CSIeff=σ×dn。

(10)

式中：n表示路径衰减指数，σ是环境因子，两者都取决于独特的室内环境。公式(10)即为本文提出的传输模型。相比公式(5)，公式(10)更简明，且由于其是在适用于室内的对数距离路径损耗模型上改进得到的，所以比公式(5)更适用于室内定位。

4 实验与分析

4.1 实验装置与环境

实验中使用型号为TL-WR886N的无线路由器作为发射端，接收端为联想笔记本电脑，其CPU为Intel Core i7-7500U，操作系统为Ubantu14.04，并且安装了INTEL WIFI LINK 5300无线网卡。由上文可知，这样的配置可以获取到CSI信息。

分别在实验室和走廊这两个环境下进行实验。实验室的场景如图2所示。整个实验室为5 m×6 m的长方形区域，参考点与接入点(Access Point,AP)的位置如图3所示。走廊的宽为2 m,长为8 m,实验布置如图4所示。

图2 实验室照片Fig.2 Laboratory environment

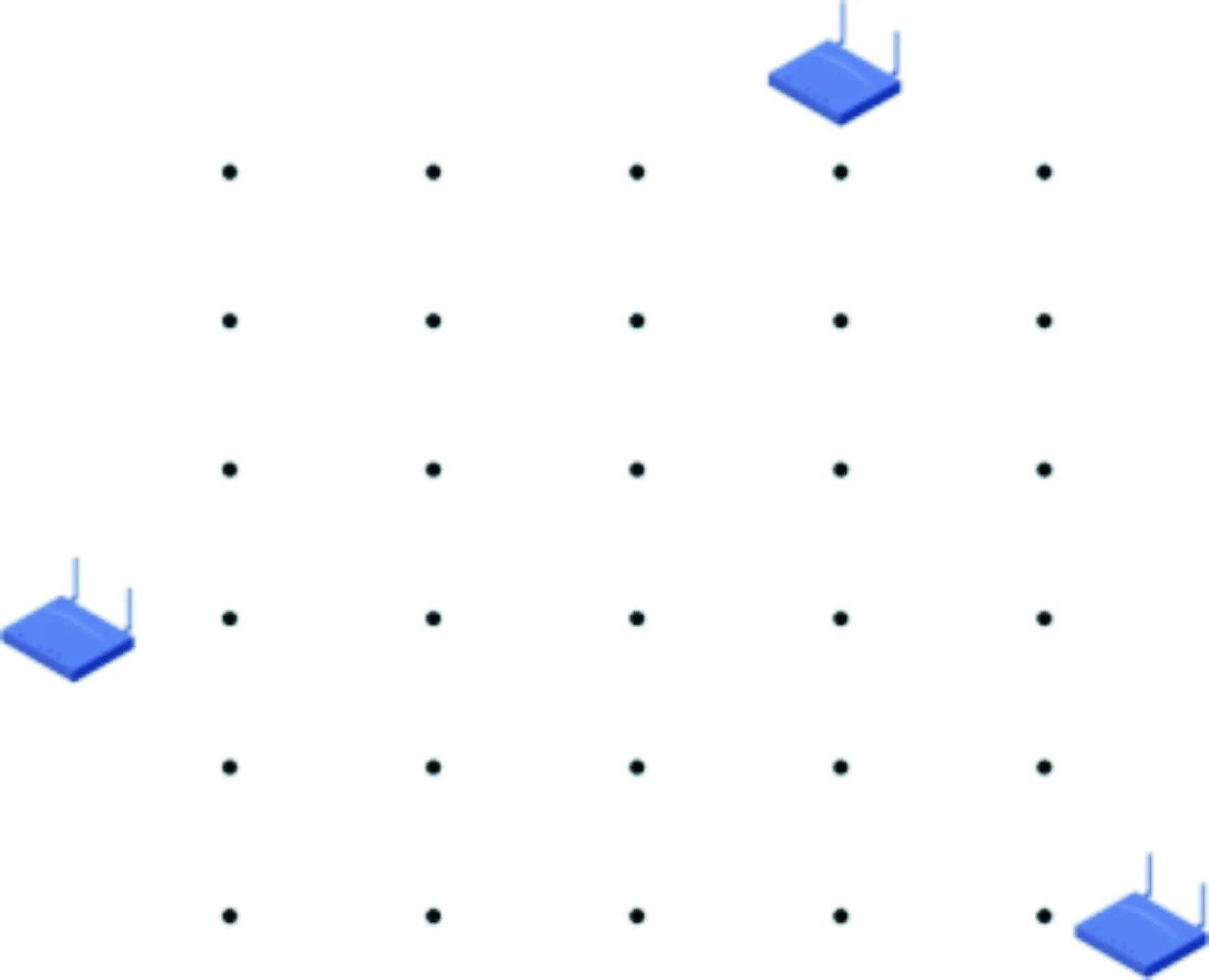
图3 实验室区域图Fig.3 The coordinates in laboratory

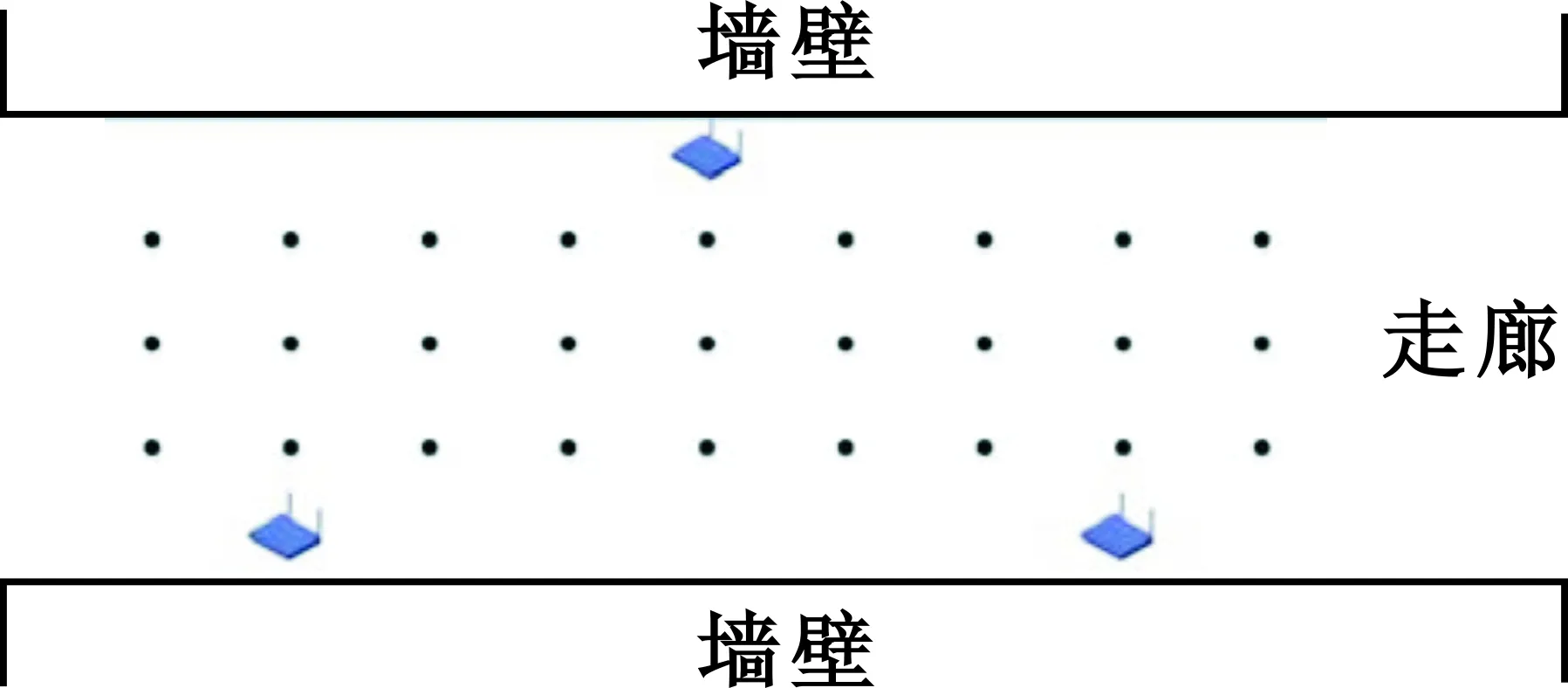
图4 走廊区域图Fig.4 The coordinates in corridor

两个场景中AP的位置坐标与参考点的实际坐标是已知的，笔记本电脑在每一个参考点获取来自3个AP的信号CSI信息，如2.2节所述，它是一个Ntx×Nrx×30的三维矩阵，并通过公式(4)计算出其有效值CSIeff。接下来验证CSIeff与距离d的测距模型，即公式(10)。

4.2 验证测距模型

实验测得CSI有效值与距离的关系如图5所示，离散的点表示在与发射端不同距离的参考点上所获得的CSI有效值。

图5 CSI有效值与距离的关系Fig.5 The relation between CSI and distance

从图5可以看出，随着发射端与接收端距离的增大，接收端获得的CSI有效值逐步减小，所拟合出来的曲线表示CSI有效值随着距离的增加而衰减的方程，即前面提出的传输模型——公式(10)。经拟合计算，σ值为120.5，n值为-1.123。

4.3 实验结果

利用拟合得到的测距模型测得每一个参考点距离3个AP的距离后，再通过三边定位法结合AP的位置坐标计算出每一个参考点的预测坐标。用参考点的预测坐标与实际坐标之间的欧氏距离表示实验误差，并计算不同误差的累积分布函数(CDF)，结果如图6～8所示。

图6中的两条线分别表示了在实验室环境下，本文(基于CSI)与基于RSSI的定位误差概率分布，可以看出，基于CSI的测距定位方法有90%的参考点定位误差在2 m以内，50%的参考点定位误差在1 m以内，而基于RSSI的测距定位方法只有50%的点误差在2 m以内，不到20%的点误差在1 m以内。因此，基于CSI的室内定位精度明显高于基于RSSI的定位方法。

图6 本文和基于RSSI的实验结果对比(实验室)Fig.6 Comparison of CSI and RSSI methods in laboratory

图7对比了在实验室环境下，本文与FILA系统的实验结果。从图7可以看出，本文的定位方法可以将90%的参考点误差控制在2 m以内，相比FILA系统提高了将近20%的概率，提高了定位精度。图8对比了在走廊环境下，本文与FILA系统的实验结果，可以看出，本文的定位方法可以将75%的参考点误差控制在2 m以内，相比FILA系统提高了将近15%的概率。对比图7和图8，两者在走廊环境下的定位精度都比在实验室环境下要低，这是因为走廊中两边较窄的墙壁对信号造成了较大的干扰，使更多的信号发生反射并产生多径效应，并影响到最后的定位结果。

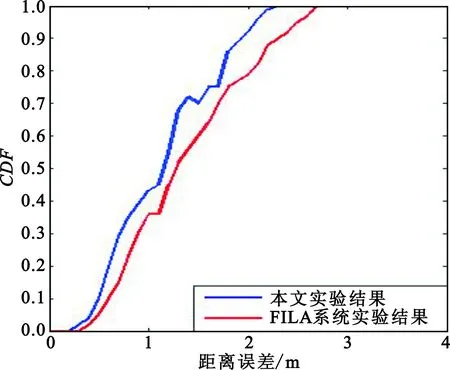
图7 本文与FILA的实验结果对比(实验室)Fig.7 Comparison between new method and FILA in laboratory

图8 本文与FILA的实验结果对比(走廊)Fig.8 Comparison between new method and FILA in corridor

图7和图8表明了在不同环境下新定位方法的定位精度都比FILA系统高，这里也印证了第3.3节中提出的距离传输模型(公式(10))的进步性，由于其是在适用于室内的对数距离路径损耗模型上改进得到的，相比由自由空间传输模型改进得到的FILA系统提高了定位精度。

5 结束语

基于RSSI的室内定位方法已被广泛研究，但是其容易受到多径效应的干扰而影响定位结果。为了克服这一问题，本文选取了更细粒度的CSI信息，其能区分不同路径，比RSSI更适用于室内定位。本文利用信号的CSI值对室内定位进行研究，在对数距离路径损耗模型的基础上改进提出适用于室内的传输模型，建立了CSI值与传输距离的关系，并利用目标位置测得的CSI值回归出其与AP的距离，并通过三边定位法预测出目标坐标。经实验评估，在实验室和走廊两种环境下，本文的定位方法能分别将90%和75%的参考点误差控制在2m以内，比起基于RSSI的室内定位方法以及FILA系统，分别提高了将近40%和20%的概率，所以有效提高了室内定位的精度，可以更好地实现定位。但目前的研究仅考虑了室内环境静止的情况，对于动态环境(如人走动)没有涉及，今后的工作会深入研究动态环境下利用CSI的高精度室内定位。