AAH不动点定理与二阶非线性方程的正解
徐厚生, 王 波
(1. 沈阳建筑大学 理学院, 沈阳 110168; 2. 东北大学 理学院, 沈阳 110819)
0 引 言
一些学者已经开始应用泛函形式的锥拉伸与压缩不动点定理研究非线性微分方程正解的存在性[1-15],文献[2]将Leggett-Williams不动点定理[5]进行推广, 得到如下结论。
引理1[2]设P是实Banach空间E上的锥,α是P上的非负连续凹泛函,β是P上的非负连续凸泛函,T:P→P是全连续算子。 若存在非负实数a,b,c,d使得
1) {x∈P|a<α(x),β(x) 2) 若x∈P, 有β(x)=b, 且α(x)≥a, 则β(Tx) 3) 若x∈P, 有β(x)=b, 且α(Tx) 4) {x∈P|c<α(x),β(x) 5) 若x∈P, 有α(x)=c, 且β(x)≤d, 则α(Tx)>c; 6) 若x∈P, 有α(x)=c, 且β(Tx)>d, 则α(Tx)>c; 且如果 a) 如果a b) 如果c Anderson等[2]应用引理1,讨论了二阶非线性边值问题 (1) 正解的存在性。本文分别在压缩条件和拉伸条件下, 通过引理1给出了二阶非线性边值问题 (2) 存在正解的充分条件。设G(t,s)是(2)相应齐次方程的Green函数, 即 (3) 引理2 由(3)表示的Green函数G(t,s)具有以下性质: G(t,s)在[0,1]×[0,1]上连续对称; G(t,s)≥0,G(t,s)≤G(s,s), ∀0≤t,s≤1; G(t,s)≥2tG(1/2,s),t∈[0,1/2],s∈[0,1]。 证明 前2个性质是显然的。至于第3个性质, 事实上, 从而 G(t,s)≥2tG(1/2,s),t∈[0,1/2],s∈[0,1] 定义P={x∈C[0,1]|x(t)≥0,x是对称的,x是凹的,t∈[0,1],x(t)≥2t‖x‖, t∈[0,1/2]}。易见P是C[0,1]中的锥。下面定义算子T为 易证P→7P。 设τ∈(0,1), 下面在P上定义凹泛函α为 凸泛函β为 由于x是凹的, 则 定理1 若b,c为正实数,3b≤c,f:[0,+∞)→[0,+∞)连续且满足 2)f(ω)在[0,bτ]是单调递减的, 在ω∈[bτ,b]有f(bτ)≥f(ω); 则方程(2)在P(β,α,b,c)中有一个正解x*。 ∀x∈P有 1) 若∀x∈P(α,c)={x∈P|α(x)≤c},则 则P(α,c)有界。 xM∈P(β,α,b,c) 事实上, 因此xM是凹的。 xM(t)=xM(2t·1/2)≥2t·xM(1/2)=2t‖xM‖ 故xM∈P。 则P(β,α,b,c)≠∅。 xL∈{x∈P|a<α(x),β(x) 事实上, 由xM∈P, 同理可知xL∈P, 则{x∈P|a<α(x),β(x) xJ∈{x∈P|c<α(x),β(x) 事实上, 由xM∈P, 同理可知xJ∈P, 则{x∈P|c<α(x),β(x) 3) 若x∈P,β(x)=b,α(x)≥a, 则β(Tx) 事实上, 由于x的对称性及连续性, 因此 从而 4) 若x∈P,β(x)=b,α(Tx) 事实上, 5) 若x∈P,α(x)=c,β(x)≤d, 则α(Tx)>c。 事实上, ∀s∈[τ,1-τ],α(x)≤x(s)≤β(x) 6) 若x∈P,α(x)=c,β(Tx)>d, 则α(Tx)>c。 事实上, 根据引理1, 则方程在P(β,α,b,c)中有一个正解x*。 例1 令b=1,c=3,τ=1/4。函数 满足条件: 根据定理1,方程(2)在P(β,α, 1, 3)中有一个正解。 定理2 若a,d为正实数,a≤τd,f:[0,+∞)→[0,+∞)连续且满足: 2)f(ω)在[0,a]是单调递减的, 在ω∈[a,b]有f(ω)≤f(a); 则方程(2)在P(α,β,a,d)中有一个正解x*。 ∀x∈P有 1) 若∀x∈P(β,d)={x∈P|β(x)≤d},则‖x‖=β(x)≤d,则P(β,d)有界。 若∀x∈P(α,a)={x∈P|α(x)≤a}, 则 从而P(α,a)⊂P(β,d)。 xM∈{x∈P|a<α(x),β(x) 事实上, 从而xM是凹的。 故xM∈P。 则{x∈P|a<α(x),β(x) xL∈{x∈P|a<α(x),β(x) 事实上,由xM∈P, 同理可知xL∈P, 则{x∈P|a<α(x),β(x) xJ∈{x∈P|c<α(x),β(x) 事实上, 同理xJ∈P, 则x∈Pc<α(x),β(x) 3) 若x∈P,β(x)=b,α(x)≥a, 则β(Tx) 事实上, 则a≤x(s)≤b。 由于x的对称性及连续性, 因此 从而 4) 若x∈P,β(x)=b,α(Tx) 事实上, 5) 若x∈P,α(x)=c,β(x)≤d, 则α(Tx)>c。 事实上, ∀s∈[τ,1-τ],α(x)≤x(s)≤β(x) 则c≤x(s)≤d。 6) 若x∈P,α(x)=c,β(Tx)>d, 则α(Tx)>c。 事实上, 则根据引理1,方程在P(α,β,a,d)中有一个正解x*。 例2 令a=1,d=4,τ=1/4。函数 满足条件: 2)f(ω)在[0,1]是单调递减的,在[1,16]上有f(1)≥f(ω); 根据定理2,方程(2)在P(α,β,1,4)中有一个正解。 本文应用建立在锥理论和不动点指数方法基础上的AAH不动点定理, 研究一类中与文献中不同类型的二阶非线性边值问题正解的存在性。当非线性项满足单调性和某些不等式条件时, 给出该类二阶非线性边值问题正解存在的锥拉伸与压缩型充分条件, 并且通过一些例子来说明结论的应用。




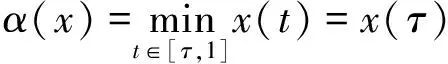
1 主要结论
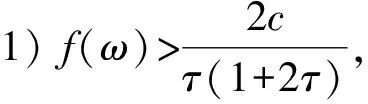


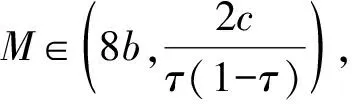

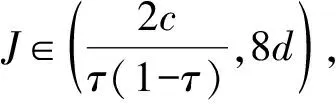




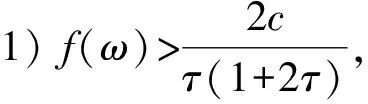
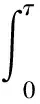


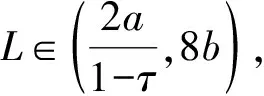


2 结 语