高温作业服装材料厚度的设计

李宁舟，郝欧亚，汪宪宏，吴宇航

（1.华北理工大学数学建模创新实验室，河北 唐山 063210；2.华北理工大学化学工程学院，河北 唐山 063210；3.华北理工大学电气工程学院，河北 唐山 063210；4.河北省数据科学与应用重点实验室，河北 唐山 063210；5.唐山市数据科学重点实验室，河北 唐山 063210）

0 引言

为设计高温作业专用服装，首先在外界温度为75℃的高温环境下进行实验，记录假人表面温度，利用热阻计算方法及傅里叶定律，根据专用服装材料的参数值，可求出导热方程中的相关系数；其次通过表示一维热传导方程[1-2]，利用泰勒级数展开可得到温度与x和t的偏导关系，选取适当的步矩，利用差分方程求解出各层温度的具体分布；最后利用二分法思想，以Ⅱ层的厚度为y轴，Ⅳ层的厚度为y轴建立直角坐标系，若满足约束条件，则在闭合区域内继续进行二分法的划分，若不满足约束条件，则在闭合区域外进行二分法的划分，最终可得到Ⅱ层及Ⅳ层的最优厚度。

1 计算高温作业服装温度分布

1.1 稳定温度分布

高温作业专用服装通常由三层织物材料构成，第Ⅲ层与人体皮肤之间的空隙可以称为第Ⅳ层，也就是说在外界环境与假人皮肤之间一共存在四层介质。当外界环境温度为75℃时，根据实验数据可以发现在稳定状态下假人皮肤外侧的温度为48.08℃。建立直角坐标系，沿x轴方向依次为Ⅰ层、Ⅱ层、Ⅲ层、Ⅳ层，各层的厚度分别为d1、d2、d3、d4。因专用服装中三层织物间无空隙，故设定五个温度分别为t0、t1、t2、t3、t4。

利用热阻计算方法和傅里叶定律[3]得到R=d/λ、ti=ti-1-qRi、q=ti-ti+1/Ri， 可 求 出 在 稳 定 状 态下这四层介质的稳定温度为：t3=61.89511℃，t4=48.08℃。得到稳定状态下这五个温度的变化趋势如图1所示。

图1 四层介质的稳定温度分布Fig. 1 Stable temperature distribution of four layers of medium

1.2 温度分布

将温度T(x,t)在(x0,t0)点沿x向前和向后泰勒级数展开Δx，有

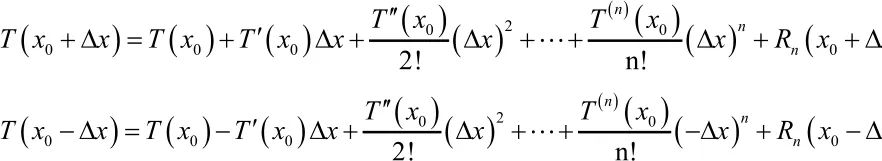
将T(x,t)在(x0,t0)点沿t向前泰勒级数展开Δt，有

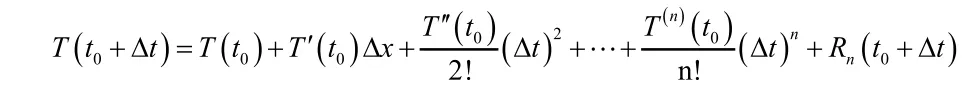
由上式可知每个位置各个时刻的温度可与之前一个时刻3个相邻位置点的温度获得，如图2所示，点(i, j)的温度受周围(i-1, j)、(i+1, j)、(i,j+1)三点温度的影响，步长Δt和Δx的取值越小，数值解精度越高。

图2 温度变化的影响Fig. 2 Influence of temperature change

根据该稳定条件λ2/cρ≤1/2，可得其中，初始条件为：T(0, t)=75，T(0, 6, t)=37，T(6, 6, t)=37，T(10, 2, t)=37，T(15, 2, t)=37(t≥0)；T(x, 0)=37(0＜0＜15.2)。当步长取 Δt=0.01s，Δx=0.1 mm时：

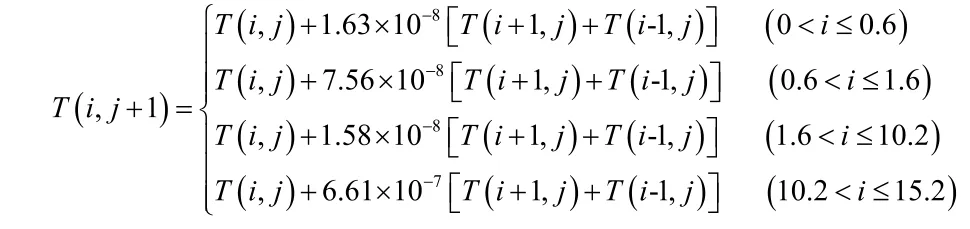
利用Excel来进行高精度一维热传导方程数值解。

2 设计高温作业服装材料厚度

二分法是指假设待查找序列和题目的要求之间的关系是单调递增的，先取区间中心，判断该处函数值和题目标准值的大小关系，如果函数值偏小，那么应该在中心右侧的区间继续查找；如果函数值偏大，那么应该在中心左侧区间继续查找，直到找到对应的值或者区间缩小到左右端点之间不再包含其他数据结束。选取步长Δt"=0.01s，Δx"=0.1mm来进行计算。

利用迭代计算功能[2]来进行数据处理时，可以用对专用服装表面温度分布进行计算；用差分方程对于服装内部温度分布进行计算。以Ⅱ层的厚度为x轴，Ⅳ层的厚度为y轴建立直角坐标系，如图3所示，0～x0代表Ⅱ层的厚度范围，0～x1代表Ⅳ层的厚度范围。x0、x1分别沿垂直x轴、y轴做直线交于一点形成闭合区域0x0Px1，取0x0的中点x2和0x1的中点x3，让x2、x3分别沿垂直x轴、y轴做直线交于一点形成闭合区域0x2P0x3。若P0点满足该约束条件，则在区域0x2P0x3内部继续进行二分法的划分，若P0点不满足该约束条件，则在区域0x2P0x3外部继续进行二分法的划分。以此类推，直至找到符合条件的最优解。

图 3 二分法设计方案Fig.3 Dichotomy design scheme

当外界环境温度为80℃，Ⅰ层厚度为0.6mm，Ⅲ层厚度为3.6mm。约束条件为在当前环境下工作30分钟，假人体皮肤外侧的温度不超过47℃，并且超过44℃的时间不超过5分钟。在该约束条件下，经过判断，P0点满足该约束条件，则在区域0x2P0x3内部继续进行二分法的划分，最终找到最优解，得到Ⅱ层的最优厚度为7.6mm，Ⅳ层的最优厚度为1.6mm。

当Ⅱ层的厚度为7.6mm，Ⅳ层的厚度为1.6mm时体表温度随时间变化情况如图4所示。

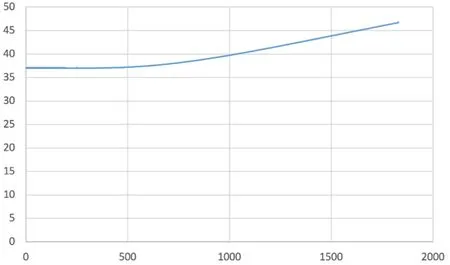
图4 最优情况下体表温度随时间变化Fig. 4 Variation of body surface temperature with time under optimal conditions