采摘机械臂结构参数对其工作空间的影响
伍辑军, 宋 欣, 杨 磊, 程祥云
(天津农学院工程技术学院,天津 300384)
在果蔬生产中,收获采摘作业约占整个作业量的35%~45%[1]。为保证果实的新鲜程度,须要在短时间内完成采摘作业,属于季节性强的劳动密集型作业。但是,随着我国城镇化进程的加快,农村劳动力老龄化和农业劳动力短缺的问题日趋严重,导致了劳动力成本的增加和采摘效率的降低。因此,大力发展和推广采摘机器人,用自动化和智能化的作业方式取代人工采摘,从而解放生产力、提高劳动生产效率和降低生产成本,具有广阔的需求空间和重要的实用价值、经济效益。
采摘机械臂是采摘机器人的重要执行部件,它的工作空间是评价机械臂工作性能的一个重要指标,描述了机械臂在结构约束下,末端参考点所能达到的空间点集合[2]。机器人工作空间求解通常采用图解法、解析法以及数值法。其中,图解法可以绘制出工作空间的剖截面,比较直观,但会受到关节数的限制[3]。解析法是通过多次包络来确定工作空间边界,并用方程表示出来,但直观性较差,计算繁琐,一般只适用于关节数少于3个的机器人[4]。数值法是以极值理论和优化方法为基础,计算机械臂工作空间边界曲面上的特征点,构成边界曲线进而再构成边界曲面[5]。这种方法的缺点是计算量太大,有些边界曲面可靠性得不到保证。在数值法中,以蒙特卡洛法[6]的使用最为普遍,适合于任何关节型机械臂工作空间求解。但是由于蒙特卡洛法是在约束条件内产生一系列随机点的云图,一方面,随机点的产生虽然符合均布分布,但仍旧随着随机性,体现为随机数目选取越多,所得到的工作空间越逼近机械臂实际工作域的近似工作域,且逼近程度取决于随机数的数量;另一方面,蒙特卡洛法没有完全考虑机械臂本身结构尺寸干涉而导致的工作空间区域减少。
因此,本研究提出采用Adams运动仿真和图解法相结合的方法来确定采摘机械臂的工作空间边界,能尽量真实且直观地表达出机械臂实际工作空间,有助于实现工作空间的精确计算。并且在采用凸包函数计算工作空间体积的基础上,开展机械臂结构参数对工作空间体积的影响分析。
1 采摘机械臂基本构型
本研究的采摘机械臂采用关节型开链结构形式,主要由基座、大臂、小臂、手腕和末端执行器组成。拥有6个自由度,分别为腰关节、肩关节、肘关节和3个腕关节(图1)。其中,机械臂的空间位置主要是由腰关节、肩关节和肘关节的参数来确定,机械臂的空间姿态是由腕关节参数来确定。

2 采摘机械臂工作空间的模拟及边界分析
本研究采用Adams运动仿真和图解法相结合的方法模拟采摘机械臂的工作空间。首先,利用Adams的运动仿真结果得到采摘机械臂在圆周范围内所能达到的极值点坐标,然后通过包络这些极值点来得到机械臂实际的工作空间。图2为机械臂在XOZ平面上的工作空间边界,其工作空间的外轮廓边界大致为x∈[-1 984.7,2 829.7] mm,y∈[-1 984,1 985] mm,z∈[-761.2,3 098.2]mm。工作空间内轮廓不规则,按照以腰关节为坐标系原点进行统计,其轮廓边界大致为x∈[-124,681] mm,y∈[-124,681] mm,z∈[0,1 065]mm,该区域内机械臂将受到结构参数限制或存在杆干涉而无法到达。
3 采摘机械臂结构参数对工作空间的影响分析
在采摘机械臂工作空间分析过程中发现,腕关节处的自由度仅对末端执行器的姿态有影响,而对于工作空间的大小不产生影响,因此在进行机械臂结构参数对工作空间的影响中可以忽略该处的自由度,得到机械臂简化示意图(图3)。

根据几何关系,采摘机械臂末端P点坐标可以表示为
x=[S+L1sinφ1+L2sin(φ2+α)]cosφ0;
y=[S+L1sinφ1+L2sin(φ2+α)]sinφ0;
z=H+L1cosφ1-L2cos(180°-α-φ1-φ2)。
(1)
3.1 采摘机械臂工作空间体积的计算方法
利用Matlab绘制出采摘机械臂工作空间的散点图,结果如图4所示。但由于散点图只提供了工作空间包络面的一个大致形态,如果须要进行工作空间大小计算的话,还要进一步对此空间生成一个较为精准的包络空间,用该包络空间的体积描述工作空间的大小。

空间中的包络面是一个一般封闭体的表面,即由所有边缘点构成的集合,生成包络面的关键在于确定全体坐标点的边缘面。为此,利用Matlab中的凸包函数convhull求出散点图的凸包点,并生成若干由三角形拼接而成的包络空间,结果如图5所示。在此基础上计算出其包络空间,即采摘机械臂的工作空间体积。
3.2 各杆件长度对工作空间体积的影响
在其他参数不变的情况下,分别计算肩高杆长S、基座高度H、大臂杆长L1、小臂轴线与肘关节距离Lv以及小臂轴线与机械臂末端距离Lh对工作空间的影响,结果如图6所示。
根据计算结果分析得到,除基座高度H外,其余4个因素皆对机械臂工作空间产生正相关影响,由拟合公式可知,杆长对工作空间的影响呈二次多项式关系。根据曲线斜率K可以分析得到,小臂轴线与肘关节距离Lv对工作空间的影响最小,其次是肩高杆长S,再次是小臂轴线与机械臂末端距离Lh,大臂杆长L1产生的影响最大。
在上述单一因素分析的基础上,采用正交试验方法,得到采摘机械臂工作空间与小臂轴线与肘关节距离Lv、肩高杆长S、小臂轴线与机械臂末端距离Lh,以及大臂杆长L1间的线性响应面回归模型:
W=-116.374 0+4.995 4×10-2S+6.157 5×10-2L1+5.35×10-3Lv+7.414 0×10-2Lh。
(2)
响应面回归模型的方差分析如表1所示,回归模型的F值为892.87,P<0.000 1,差异极为显著,证明试验是可靠的。模型确定系数R2=0.996 9,校正确定系数AdjR2=0.995 8,表明模型可以解释99.58%的响应变化,模型拟合度高,试验误差小,能够很好地描述各影响因子与响应值之间的关系。依据回归模型中的系数和方差分析可知,响应面试验范围内各影响因子的主效应关系为大臂杆长L1>肩高杆长S>小臂轴线与机械臂末端距离Lh>小臂轴线与肘关节距离Lv。
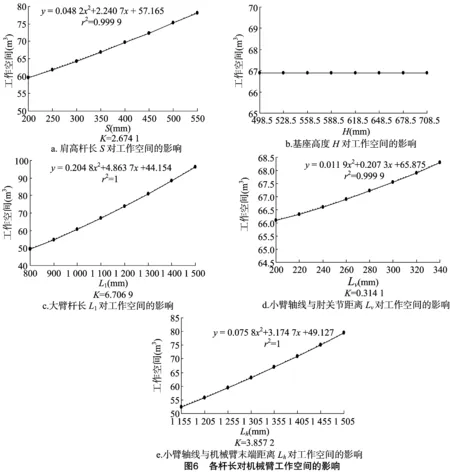
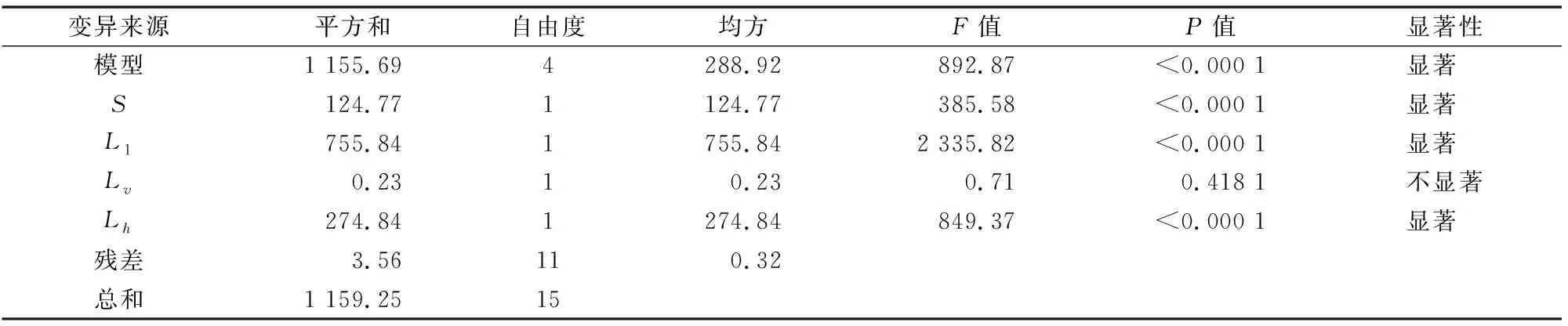
表1 回归模型的方差分析
利用20组试验数据对所建立的线性响应模型进行预测准确性验证,结果如表2所示。预测结果与试验结果的相对误差率在0.06%~0.96%之间,平均误差率为0.46%。由此可知,该线性响应回归模型具备一定的准确性,可以在设计中用于采摘机械臂工作空间的预测以及设计方案调整。
3.3 各关节转角对工作空间的影响
在其他参数不变的情况下,分别计算各关节转角对工作空间体积的影响,影响趋势如图7所示,关节转角对工作空间的影响程度如表3所示。
由分析结果可知,腰关节转角下限变动范围为-180°~-40°,上限变动范围为40°~180°,机械臂工作空间从 36.71 m3增长到71.57 m3,呈正相关趋势,即随着上限和下限范围的扩大,工作空间也会增加;图7-b中肩关节转角变化对工作空间影响的曲面呈锯齿状,其下限值变动范围为 -65°~-25°,上限值变动范围为60°~90°,机械臂工作空间从54.00 m3增长到70.95 m3,同样呈正相关趋势,其上限值对工作空间的外轮廓产生影响,而下限值是对内轮廓产生影响;图7-c中肘关节转角下限值变动范围为-80°~-10°,上限值变动范围为10°~85°,机械臂工作空间从47.02 m3增长到70.95 m3。肘关节转角下限值对工作空间的外轮廓产生正相关影响,且影响程度较大,而上限值是对内轮廓产生影响。从表3中的数据来看,腰关节对于工作空间的影响程度最大,肘关节其次,肩关节的影响最小。
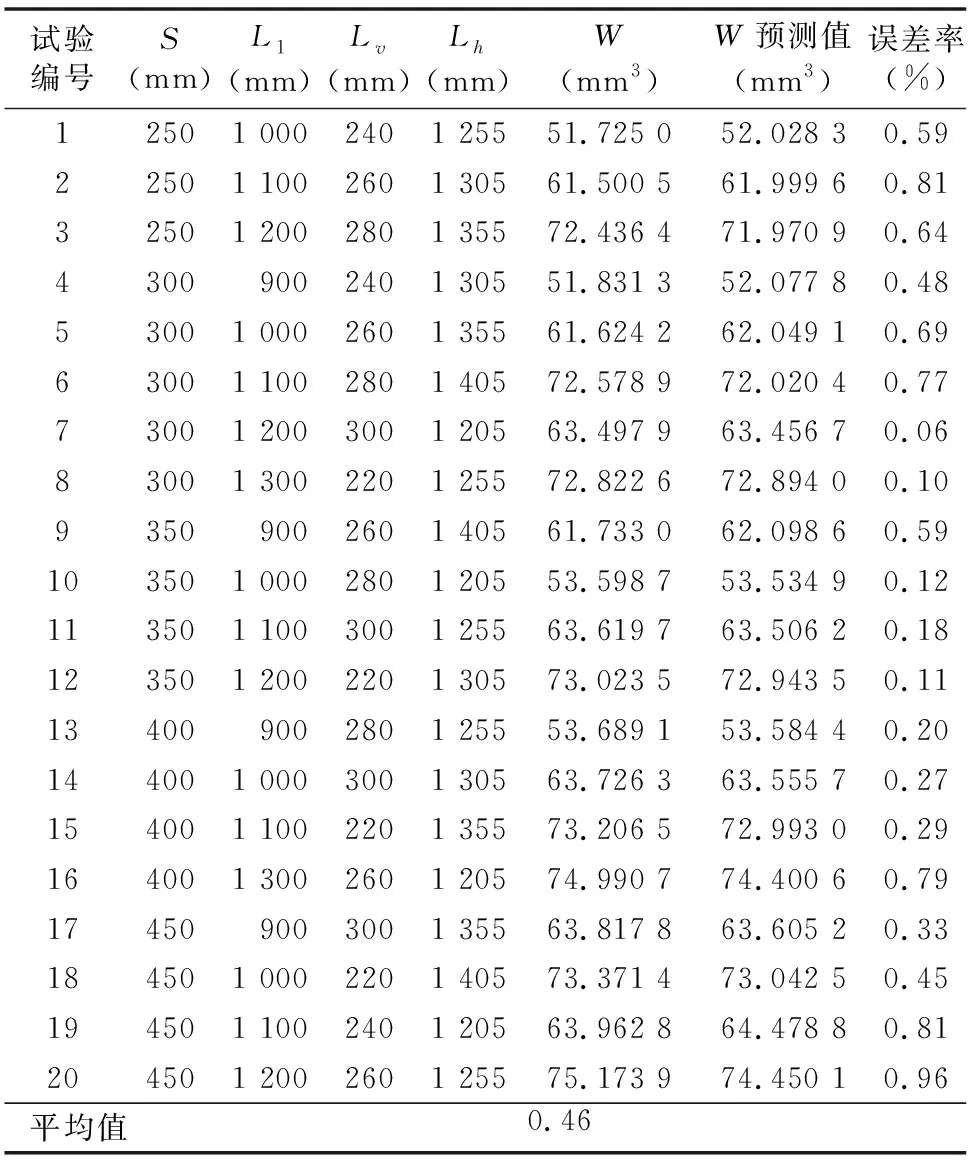
表2 回归模型预测准确性分析
4 结论
(1)采用Adams运动仿真和图解法相结合的方法模拟了采摘机械臂的工作空间,该方法相比于蒙特卡洛法更能准确地描述机械臂的可达区域。
(2)在利用Matlab绘制出采摘机械臂工作空间散点图的基础上,采用凸包函数进行处理,生成一个较为精准的包络空间来描述该工作空间的体积。
(3)通过对采摘机械臂结构参数对工作空间的影响分析,得到各杆长参数中,小臂轴线与肘关节距离对工作空间的影响最小,其次是肩高杆长,再次是小臂轴线与机械臂末端距离,大臂杆长产生的影响最大。关节转角参数中,腰关节对于工作空间的影响程度最大,肘关节其次,肩关节的影响最小。上述结论为机械臂的结构设计和优化提供了理论依据。
(4)建立了线性响应回归模型用于预测采摘机械臂工作空间以及设计方案调整,并通过试验数据验证了该模型的准确性。

表3关节转角对工作空间的影响程度
关节部位关节转角范围增长率(%)工作空间体积增长率(%)腰关节3594.96肩关节1631.39肘关节7050.89

