“十二五”时期中国碳排放全要素生产率及其影响因素研究

李小胜 胡正陶 张 娜 宋马林

一、引 言

我国政府在“十二五”时期提出单位 GDP能耗和二氧化碳排放在“十一五”时期的基础上分别再降低16%和17%以及主要污染物排放总量减少8%～10%的目标。从目前环境保护部和国家发展和改革委员会数据看，该目标已经顺利完成，这些任务的完成与国家命令控制型工具和经济激励措施的双重作用是分不开的。十八届五中全会我国政府又指出“十三五”时期经济要坚持绿色发展，积极推进生态文明建设，全面节约和高效利用资源，建立健全碳排放权初始分配制度，推动形成勤俭节约的社会风尚，这说明未来一段时间，节能减排仍然是政府关注的焦点。

“十二五”时期是我国节能减排的关键时期，我国节能减排效率如何？准确评价过去绿色发展和节能减排的工作成效，对于“十三五”时期绿色发展、控制碳排放和建立碳交易市场制度都具有重要的参考意义。国内很多文献对碳排放效率和碳排放全要素生产率指数进行研究，从最初的没有考虑非期望产出，到考虑非期望产出情况，得出了很多有益的结论。但由于处理的方法不同，不同的研究方法得出的结论差别很大，究其原因包括：是否考虑非期望产出；考虑非期望产出的模型，采用方向性向量时是否调整比例一致，很多研究采用考虑非期望产出的方向性距离函数方法，但是这种方法通常采用所有要素调整都按照同一个比例进行调整，这不是真正的碳排放效率；在采用方向性距离函数的方法时，很多研究都应用的是径向的调整，没有考虑到松弛的作用。这些问题的存在都表明以往的碳排放效率测算以及基于效率的碳排放全要素生产率指数计算仍然存在着改进的余地。

二、文献综述

虽然测算碳排放效率和碳排放全要素生产率指数的文献很多，但是很多文献没有考虑上述的三个问题以及个体的异质性问题。最近大量文献认为异质性问题比较突出，异质性表现在决策单元的地区不同、类型和所有制不同、规模大小不同等方面。如果不考虑异质性将所有决策单元放在一起进行效率评价会得到有偏的结果。考虑异质性的共同前沿分析思想来源于Hayami和Ruttan(1971)提出的“Meta-frontier”(共同前沿)概念，后来该思想被很多研究者广泛应用在制造业效率、能源效率和碳排放效率的测量中(O’Donnell等，2008)。由于传统的技术效率分析将不同的决策单元(DMU)生产技术看成是同质的，具有不可比性。共同前沿分析有效回避所有时期或所有决策单元采用相同的生产前沿，可以将决策单元划分为不同的组别，每个组别形成组别前沿(group frontier)，这样避免因缺乏统一的标准而无法找到效率缺失的存在。共同前沿的分析方法中，早期应用的都是参数模型，Battese和Rao(2002)、Battese等(2004)在异质性条件下采用参数共同前沿分析方法研究了技术效率和技术缺口问题。O’Donnell 等(2008)又提出了一种非参数的共同前沿分析方法研究技术效率，Oh(2010)采用考虑非期望产出情况下的非参数共同前沿模型对环境效率进行评价，Oh和Lee(2010)同时采用没有考虑非期望产出的非参数共同前沿模型分析58个国家1970—2010年的全要素生产率指数情况。Fei和Lin(2016)采用共同前沿的分析方法对中国各个地区的农业碳排放效率进行了详细的分析。

由于技术效率测量的是决策单元间静态的相对比较，为了动态分析效率的变化，很多文献计算了全要素生产率指数。采用共同前沿的分析方法得到效率后计算全要素生产率指数是较为稳健的方法。但是很多研究采用方向性距离函数进行全要素生产率指数计算时，对各个要素调整比例采用相同的比例假定，这制约了全要素生产率指数的准确性。例如，Oh(2010)、Oh和Lee(2010)、Zhang和Choi(2013)采用的都是所有要素调整按照相同比例的方式测算效率之后，再基于效率计算全要素生产率指数。Munisamy和Arabi(2015)首先注意到这个问题，他们采用各要素都调整1为度量单位，但调整比例不同的形式，对全要素生产率指数进行测量，发现意大利48个热电厂2003—2010年效率和全要素生产率指数增长的都较快。

同样国内学者也注意到采用共同前沿分析方法是测算全要素生产率指数较为稳健的方法。由于我国各地区经济发展的极度不平衡，并且能源消费和二氧化碳排放的区别较大，根据各个省份的不同情况进行分析，按照共同前沿分析的思想能够更细致准确地度量各地区二氧化碳排放的效率、全要素生产率指数的大小及其影响因素，有利于做出不同的切实可行的碳减排计划。Wang等(2015)认为中国各个地区的经济规模、产业结构、地理和资源环境的情况不同，生产技术的差异性存在，所以在评价效率的时候必须考虑异质性。李胜文等(2013)认为对不同省份的效率进行测量的前提是技术水平相当，而国内有些文献在采用数据包络分析和随机前沿分析构造共同前沿的时候忽视了这点，将全国看成一个整体，导致技术效率计算结果的不可比。在认识到技术效率差距的前提下，他们将中国各省区分为东、中、西部地区，应用共同前沿方法对技术效率和技术差距进行研究。王群伟等(2014)利用共同前沿和非径向DEA方法对58个国家和地区1995—2007 年二氧化碳排放绩效进行测量。沈能等(2013)充分考虑农业环境技术差距，将中国各地区分为东部地区、中部地区和西部地区，划分为三个技术异质性组群进行效率测量。

上述的研究中，国内和国外的学者已经采用共同前沿的方法对技术效率和全要素生产率指数进行测度，但是采用的是径向方法或者是方向性距离函数的方法，在利用方向性距离函数方法时，应用的都是所有投入和产出(包括非期望产出)，按照相同比例，依据自身数据的大小进行调整。但调整比例大小一样，得到碳排放效率不是真正意义上的碳排放效率。其次，碳排放效率测量的前提是所有决策单元都具有类似的技术水平，但中国各地区经济发展水平存在着较大的差距，技术水平也不一样。共同前沿的分析方法明显较传统的不考虑异质性的方法好。本文的目标就是在考虑各个要素调整比例不一致的情况下，运用共同前沿技术测量各个省份“十二五”时期的碳排放效率；在测算碳排放效率的基础上，采用共同前沿Malmquist-Luenberger生产率指数方法测量全要素生产率指数并进行分解；接着我们对影响全要素生产率指数的因素进行实证分析，分析各影响因素的作用大小；最后给出结论和具体的政策建议。

三、研究方法

（一）环境生产技术

我们将每个省份看成是一个决策单元，有K个省份，i=1,…,K，每个省份应用投入要素 x∈，生产出期望产出y∈和非期望产出 b∈，时期为t=1,…,T。环境生产技术可以表示为P={(x,y,b)x 能 够生产出(y,b )}。环境生产技术满足三条公理：(1)投入和期望产出是强可处置或可自由处置的，即如果(y,b )∈P(x)，且y'≤y，那么(x;y',b )∈P(x)；(2)非期望产出是弱可处置，即(y,b)∈P(x)时，0≤θ≤1会有(x;θy,θb)∈P(x)成立，这个条件表明期望产出和非期望产出具有联合弱可处置性，即减少污染是有成本的；(3)零结合性，当(x;y,b )∈P(x)时，并且有b=0，那么必有y=0，该性质称为零结合性，即没有非期望产出就没有期望产出。

实际的生产过程是追求期望产出最大化同时希望非期望产出最小化，这种思想直到Chung等(1997)提出方向性距离函数时才很好的解决，方向性距离函数可以对产出和投入按照不同的方向进行调整，使期望产出最大化，投入和非期望产出最小化。方向性向量的选择不同，方向性距离函数的结果也不一致，本文采用(gxnk, gymk, gblk)=(− xnk, ymk, − blk→)表示，即以自身数据的大小为方向性向量调整距离，那么方向性距离函数可以表示为其中投入向量x包括资本、劳动和能源消耗，期望产出变量y用地区生产总值表示，非期望产出b用地区的碳排放表示。方向性距离函数我们采用下面的Russell型线性规划模型得到。

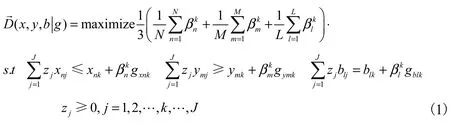
从规划模型(1)和方向性向量的选择可以看出，对于期望产出、投入和非期望产出的调整距离大小可以不一致，如果都为 0，那么说明该省份处在前沿面上，上面的距离结果越大，说明该决策单元的效率越低，离前沿面的距离越远。

上述的效率评价模型通常将所有的决策单元放在一起进行构造前沿面，通过测算各个体离前沿面的距离来分析效率的高低，通常被认为没有区分决策单元的异质性(group heterogeneities)。实际上，不同技术水平的地区前沿面是明显不同的，为了解决这个问题，Oh(2010)提出考虑非期望产出情况下的共同前沿模型，该模型在共同前沿的假定下结合传统的Malmquist-Luenberger生产率指数对效率和全要素生产率进行评价，结果相对合理和稳健。本文将利用上述的Russell型距离函数公式得到真正意义上的碳排放效率，然后再按照共同前沿方法测量中国各地区的技术效率和 Malmquist-Luenberger生产率指数。

（二）基于各要素调整比例不同的共同前沿Malmquist-Luenberger生产率指数

为了能够得到共同前沿模型中各地区的技术效率，需要对各个地区按照技术水平类似的原则进行分组，得到相应的三类环境生产技术：同期的环境生产技术、跨期的环境生产技术和全局的环境生产技术。假设总体决策单元一共有H组，h=1 ,2,…,H，对于具体的R组，同时期的环境生产技术可以表示为

h以同一个时期的该组所有决策单元构造的前沿面表示的技术。跨时期的环境生产技术可以表示为，表示该组不同时期的决策单元放在一起构造前沿面，再根据此前沿面计算得出各决策单元各时期的技术效率大小。全局环境生产技术可以表示为，表示所有决策单元的所有时期为参考前沿面，再计算各个地区不同时期的技术效率。

在以上三种共同前沿环境生产技术下，可以利用式(1)的方向性距离函数测量得到各个决策单元离前沿面的距离，即技术效率值。因此，可以根据Chung等(1997)的定义，计算得到同时期的Malmquist-Luenberger指数(ML)，该指数可以表示为：

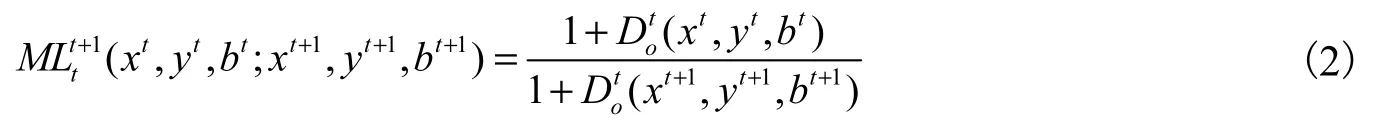
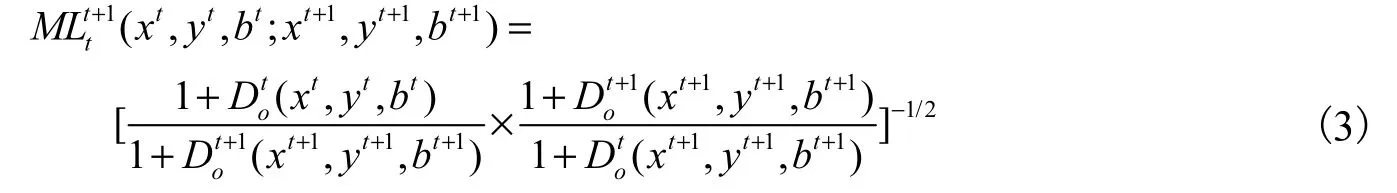
对于跨时期的共同前沿Malmquist-Luenberger全要素生产率指数(ML)的计算，可以用下面的公式表达：

对于跨时期共同前沿 Malmquist-Luenberger生产率指数我们可以对其进行分解，表示为技术效率变化(TE)和离最佳实践前沿面的缺口(BPG)的乘积：

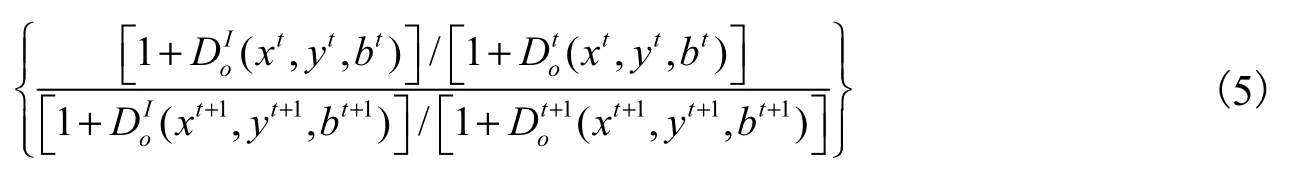
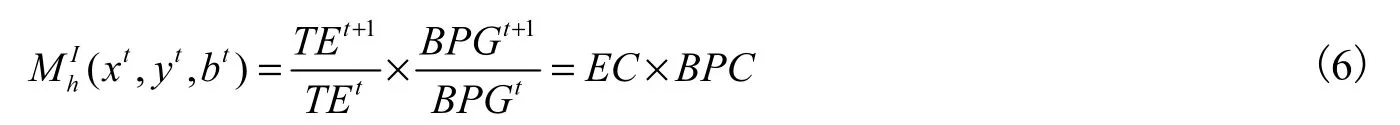
最后，基于不同要素调整比例的共同前沿全局Malmquist-Luenberger生产率指数，可以定义为式(7)：

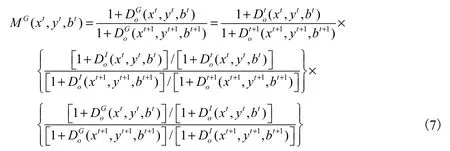
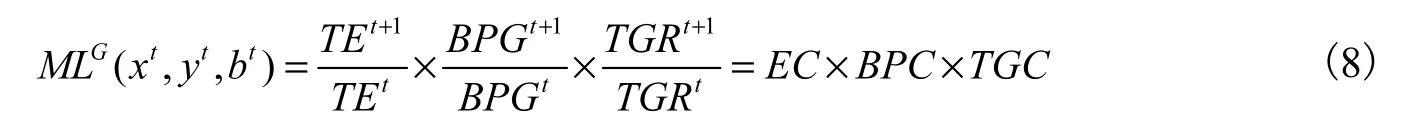
其中，TEt仍是技术效率，表示某个决策单元离第h组t时期构造的前沿面距离，越大技术效率越高，EC表示相邻两个时期的技术效率改变。BPGt表示第h组t时期构造的前沿面与所有时期构造的前沿面距离，越大表示t时期构造的前沿面离该组所有时期构造的前沿面距离越近，BPC表示最佳实践前沿面缺口的改变，反映创新效应或者技术进步的效应。TGRt表示第h组所有时期构造的前沿面与所有组所有时期数据构造的前沿面距离，越大表示该组与整体的距离越近，其中TGR表示技术缺口比率，TGC表示技术缺口比率的改变，即特定组技术与领先组之间的差别。与传统的 Malmquist-Luenberger指数一样，跨期和全局的全要素生产率指数的变化大于1表示全要素生产率指数上升，小于1表示全要素生产率指数下跌，等于1表示全要素生产率指数没有变化。如果我们以群组1为例，假设时期1和时期2的产出分别为a1和a2，o1和o2分别是生产的起点，且o1a1和o2a2的距离都为1，那么全局性全要素生产率指数可以表示为式(9)：

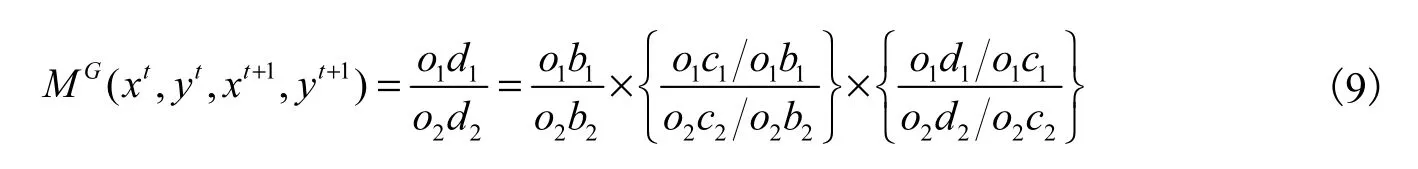
其中，式(9)中最后的等式第一项反映的是技术效率的改变，第二项反映的是离最佳实践前沿面距离的改变，最后一项反映的是技术缺口比率的改变，就是跨期的前沿面与全局的前沿面的距离。

（三）数据来源

本文以中国30个省、市、自治区“十二五”时期的资本、劳动和能源作为投入要素，以各地区 GDP和二氧化碳排放作为产出对碳排放效率和碳排放全要素生产率进行分析。各地区的生产总值数据来自中国统计年鉴，并对该指标按照国内生产总值指数进行不变价处理。能源消耗来自《中国能源统计年鉴》。劳动数据来自《中国统计年鉴》，采用年初和年末劳动力人数的平均表示，单位为万人。资本存量采用尹向飞和段文斌(2016)的处理方法，按照“永续盘存法”进行核算，并对后续数据扩充，并采用不变价进行表示，单位为亿元。二氧化碳数据国内外研究都从能源消耗的角度进行估计，本文按照李小胜和宋马林(2015)的文献对该指标进行估计，单位为吨。2013—2015年的数据参考Wang等(2013)观点，国内生产总值按照年均7.5%的增长速度推算得到，碳强度按照年均下降3.8%的速度外推得到，资本存量按照平均增长速度为14%得到，从业人员按照增长速度为0.622%计算得到，能源消耗强度按照16%的速度递减得到，由于西藏自治区数据不全，本文只研究了中国大陆30个省份的投入产出数据。

四、实证结果分析

（一）技术效率分析

采用共同前沿的分析方法研究碳排放效率和碳排放全要素生产率，首先需要对群组进行划分，按照国家统计局的地区进行分类，其中由于西藏数据不全，我们将其从西部地区中剔除。即东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南；中部地区包括山西、吉林、黑龙江、安徽、江西、河南、湖北、湖南；西部地区包括内蒙古、广西、重庆、四川、贵州、云南、陕西、甘肃、青海、宁夏、新疆。

1.各地区全局的技术非效率

全局的技术效率测量是指不同地区各时期与所有组群中的个体所有时期构造的前沿面相比距离是多大。在全局环境生产技术的约束下，按照公式(1)，我们计算得到2011—2015年各个地区的技术非效率值(如表1)。从表中的结果可以看出，按照全局的效率进行测量，除广东省外，各个地区都存在着非效率的情况，特别是一些不发达地区离前沿面的距离较远，相反，我们发现“十二五”时期发达地区的效率非常高，即非效率项的值小，广东省在 2011—2015年间每年都是处在效率的前沿面上，说明广东省的投入和产出组合得非常好，即使在全局效率测量下，前沿面组合结构比较复杂的情况下，仍然各期都是有效率的。2011—2015年东部公认的发达省份北京、上海、浙江和江苏的技术效率都在 80%以上，东部地区的辽宁、山东和河北效率较低，特别是辽宁各年份的非效率都在50%以上，其次是山东省非效率项在35%以上，这个结果与李小胜和宋马林(2015)的结论是一致的，山东省虽然经济总量很大，但是污染排放也较大，考虑所有的投入和产出组合后非效率项数值仍较高。2012年后广东、上海、北京、江苏、天津、浙江这6个发达省份始终处在前沿面的最前端。中部地区的各个省份非效率数值都在28%以上，效率均非常低，特别是山西省，在中部的8个省份中效率最低，非效率值在75%以上，这与多数文献的结论是一致的，山西省是一个资源型大省，能源消耗较大，导致碳排放效率低。其次中部效率较低的省份是吉林和河南两省，这两个省份的特征较为类似，经济总量在中部地区也偏大，但是能源消耗也大。西部11个省份与东部和中部相比效率更低，绝大多数省份的非效率项明显高于前两个地区，西部地区的宁夏在所有年份都是效率最低的地区，每年的非效率项都在88%以上，这表明按照全局性技术效率的测量，宁夏投入产出组合最无效。实际上这个结果与宁夏的碳排放强度是紧密相连的，宁夏的碳排放强度是全国所有省份中最高的，这也从某种意义上表明全局效率测量方法在碳排放效率计算中的合理性，共同前沿分析方法是未来碳排放效率测量中应该值得提倡的测量技术。

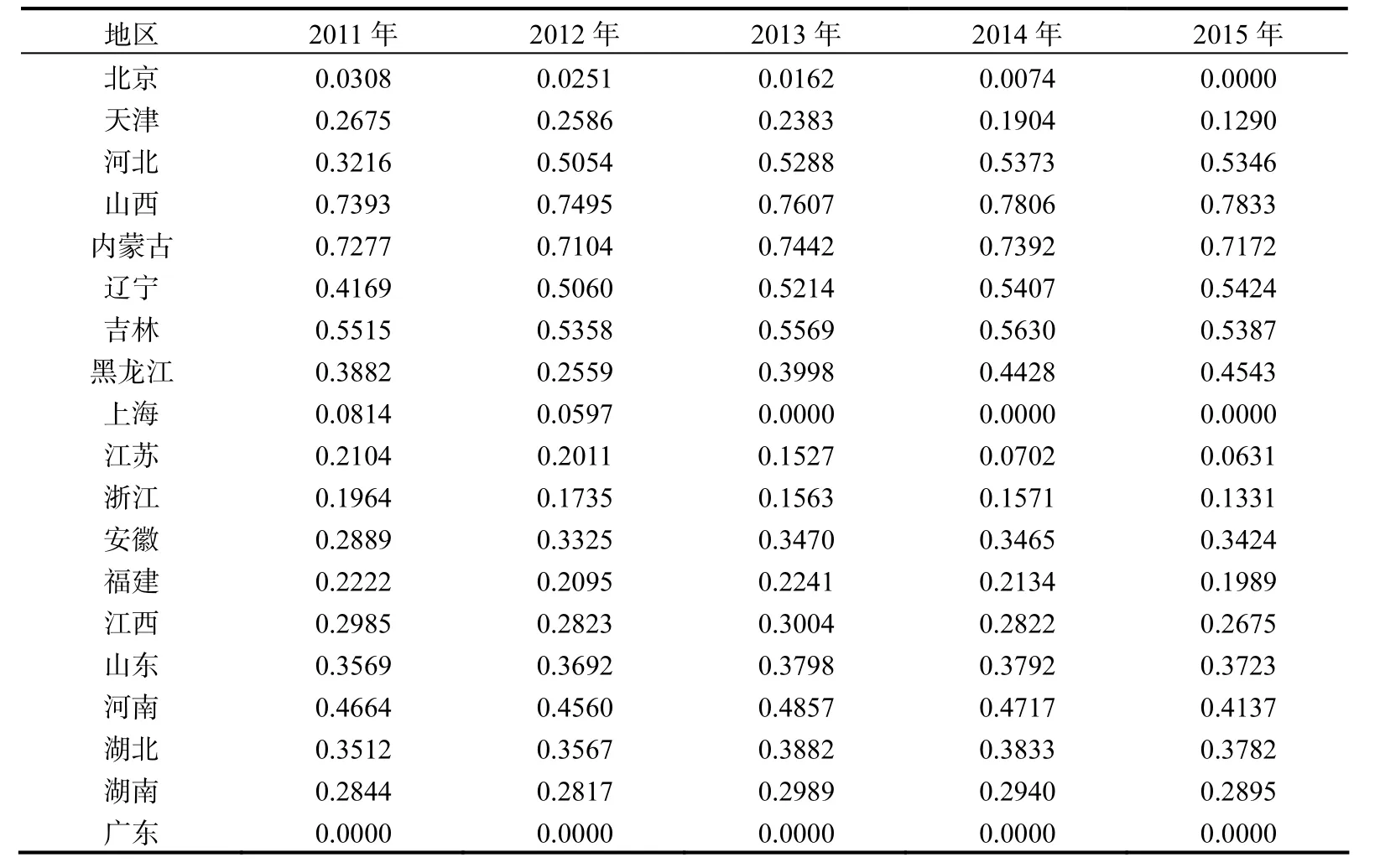
表1 各群组中的地区在全局技术下的非效率值

续表1

2.各地区跨期的技术非效率

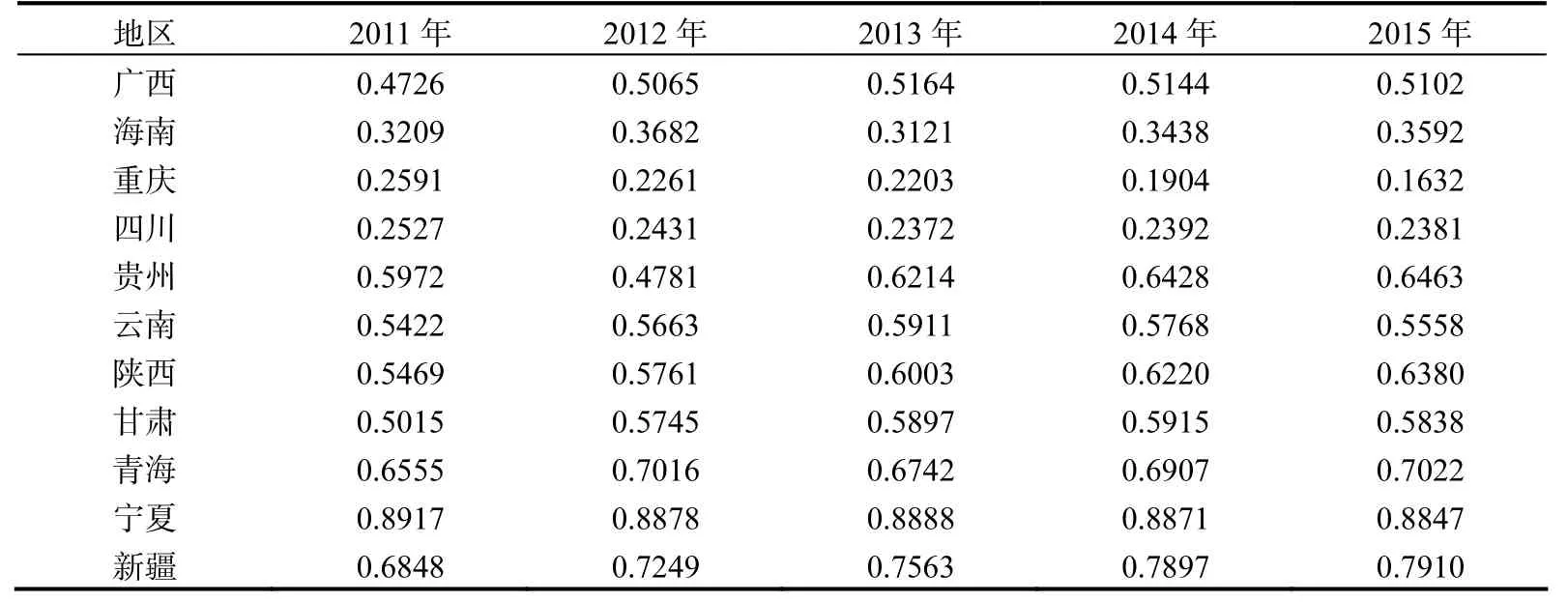
跨期的群组技术效率是指该群组中各地区离该群组所有地区所有时期构造的前沿面距离。跨期的群组环境技术可以用表示，在这种技术下，采用距离测量式(1)，我们可以得到各个地区的技术非效率值(如表2所示)。通过分析表2中的数据，我们发现一个非常有意思的现象，分组的情况下各个地区的非效率出现了较大的变化，中部地区除了吉林和湖北有非效率的情况外其他省份都没有非效率情况出现，而且各个省份之间的非效率相差非常得小。这从某种程度上可以看出，这些省份的投入和产出结构没有多大的差异，群组的划分还是比较正确的，也进一步表明该群组在以不同时期的数据构造前沿面时是合理的，跨期的技术效率测量结果离前沿面的距离比全局效率测量的值更小。其次，东部11个省份中，各年技术效率数值较高的依次是广东、北京和上海，同样河北、辽宁和山东的技术效率仍较低，其他几个省份的非效率数值在 0.2左右，离前沿面的距离不是很远。但是中部各个省份之间的差别比较大，很多省份虽然出现了非效率的状况，但是与全局的非效率测量来看，数值明显小于后者。同样西部地区的效率还是较低的地区，西部省份中仍然是宁夏和青海的技术效率最差，宁夏的技术非效率每年都达到 80%以上，西部效率较高的省份是内蒙古、四川和重庆，其他省份的技术非效率也是维持在 20%左右，但是这种划分省份测算的效率结果没有中部技术效率测算结果之间的差距小，说明这一组个体之间存在着一定的差异，群组的同质性没有中部地区好。

表2 各个群组中的地区在跨期技术下的非效率

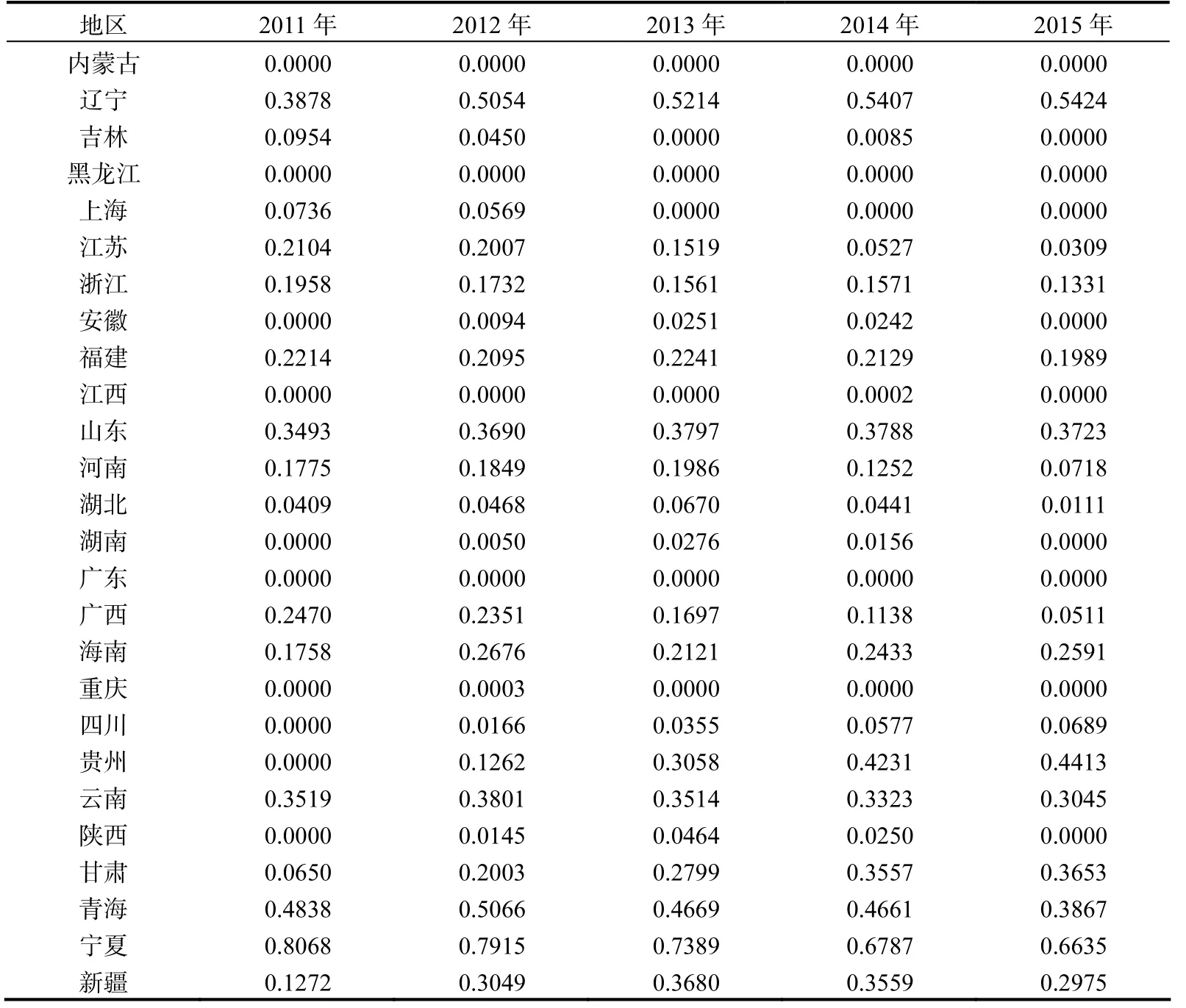
续表2

3.各地区同时期的技术非效率

同时期的技术效率测量与传统的效率测量是一样的，只不过对地区进行了划分，形成了各群组的共同前沿，时期上并无太大不同，用来反映各个省区在当期单个群组情况下的非效率结果。对于各个地区同时期的技术非效率我们采用式(1)在生产技术约束下得到的结果(表3)。同时期的生产技术参考前沿面比上述的两种技术效率测量都少，所以形成的效率明显高于上述两种结果。从表3中我们看到东部地区的广东、海南、上海和北京各年都是处在前沿面上，非效率项的数值为 0，是最有效率的地区，效率较低的省份仍然是辽宁、山东、福建和浙江，但是这些省份的效率数值明显高于前面两种技术下的效率值。中部地区除了河南和湖北存在着非效率现象，其他省份都不存在非效率状况，且全局的非效率项和跨期的非效率项数值大于当期的非效率状况。西部地区的宁夏、云南和青海的非效率状况持续最差，但是与前面两种碳排放测量技术相比还是低些，同样西部其他省份的非效率数值比较小，与实际经济表现相一致，从上面的三种效率测量的技术看，共同前沿效率分析模型是合适的：一方面能够区分出效率低的省份，另一方面通过群组的划分，可明显发现不同的环境生产技术下各种效率测量的大小差别。

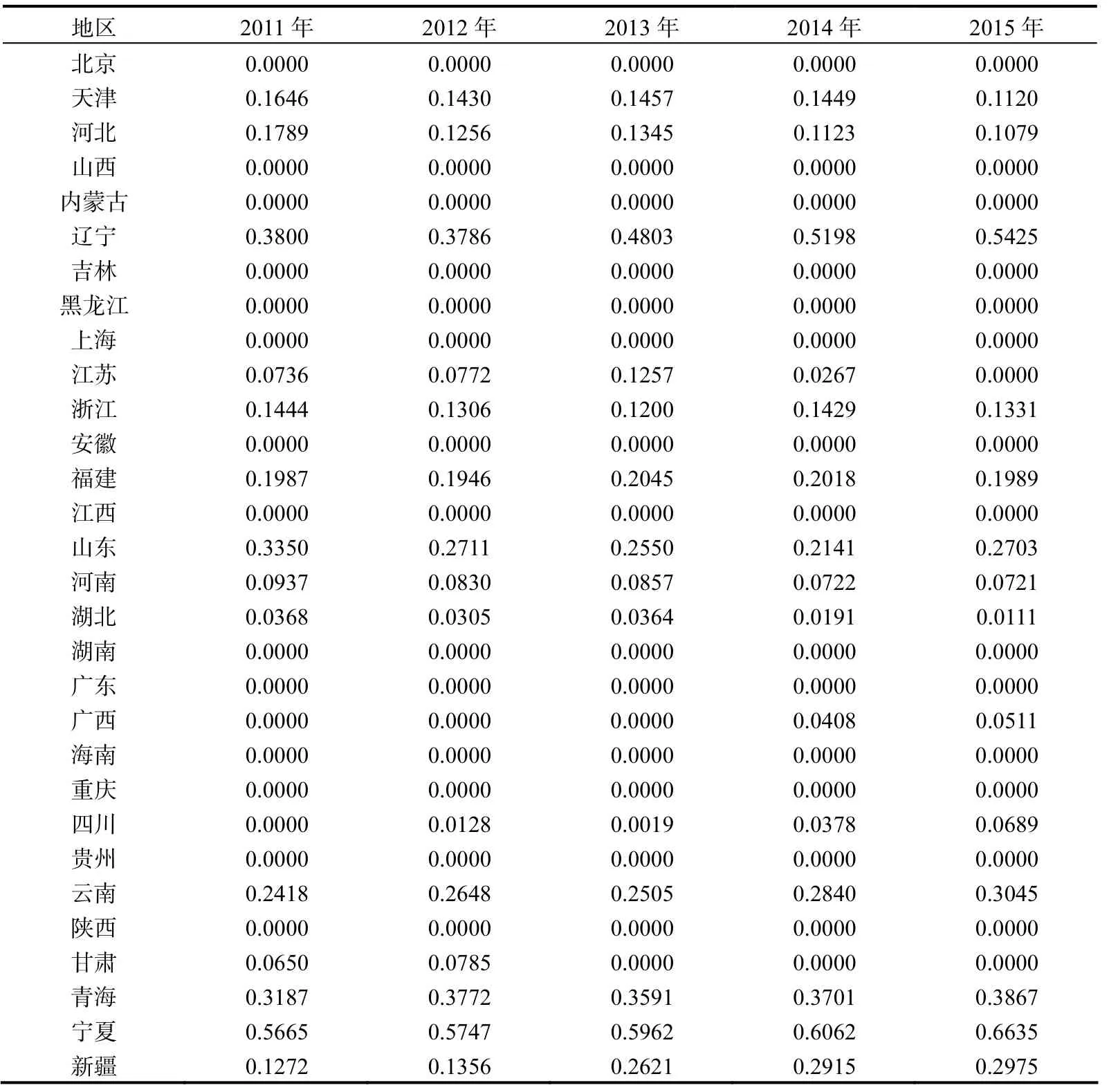
表3 各个群组中的地区在同时期技术下的非效率

综合上述的三种效率分析结果，我们可以看到，无论是采用全局的效率分析，还是跨期的效率分析和当期的效率分析，效率不高的地区通常是经济不发达的中、西部地区，也是资源生产和消耗较大的地区。我们从国家统计局收集到2005—2011年全国30个省份能源消耗强度指标，即万元国内生产总值的能源消耗数据，各年这几个省份的能源消耗强度始终是最高的，特别是宁夏自治区逐年的能源消耗强度都在每万元GDP能源消耗为 3吨标准煤以上，在全国是能源消耗强度最高的省份，贵州省在 2005—2007年这3年也是能源消耗为3吨标准煤/万元GDP左右。但是这些能源消耗强度高的省份能源消耗下降的速度和绝对量也是非常大的，宁夏自治区从2005年4.14吨标准煤/万元GDP下降到2011年的2.28吨标准煤/万元GDP，年均下降速度达到10%，即使是这样能源消耗强度还是远远高于其他发达省份。2011年能源消耗强度最低的省份是北京为0.46吨标准煤/万元GDP，宁夏是北京的能源消耗强度的5倍，可见能源消耗强度相差较大，这也佐证了宁夏等不发达省份效率非常低的原因。综合上述三种效率测量结果我们发现全局的非效率数值大于群组的非效率值，群组的非效率值大于当期的非效率，前沿面构造中的地区越多，各个地区与前沿面相比效率越低，共同前沿模型的规律较为明显。

（二）各要素调整比例不同的共同前沿全要素生产率指数分析

1.基于共同前沿的Malmquist-Luenberger全要素生产率指数

基于共同前沿模型的效率分析是从静态比较的角度对各个地区离前沿面的距离进行阐述，不能够反映效率的动态变化，为了动态研究效率的变化，我们需要计算全要素生产率指数，该指数从动态比较的角度对各地区的不同时期效率进行比较评价得到指数，比上述静态效率计算提供的信息更多，也更加全面和详细。根据上述的三种效率测量结果，利用式(7)我们就可以得到各个地区的全局Malmquist-Luenberger全要素生产率指数(表4)。从表中全要素生产率指数可以看出发达省份中的北京、天津、浙江、上海、海南、广东的全要素生产率指数都在100%以上，相反，宁夏、青海、甘肃各年的全要素生产率指数都在1以下，出现了全要素生产率指数的下降状态。其他省份的全要素生产率指数出现了交替的变化，但是大多数年份各个地区的全要素生产率指数都是上升的状态。

按照共同前沿全局Malmquist-Luenberger生产率指数的计算，2012年全要素生产率最高的是海南省为103.59%，青海省的全要素生产率指数为97.29%(最低的省区)，其他省区的全要素生产率指数都接近1，没有发生大的变化。2013年全要素生产率指数增长较多是上海市为105.97%，青海省的全要素生产率指数为98.16%(当年最低)，其他省份的全要素生产率指数都接近100%。2014年所有地区的全要素生产率指数都出现了上升情况，其中江苏省的全要素生产率指数上涨最多为107.71%，全要素生产率指数最低的省份是青海省为99.02%，天津、山东等发达地区的全要素生产率指数都处在增长较快的地区，2015年全要素生产率指数与2014年一样，多数省份的全要素生产率指数出现了上升并且接近1，全要素生产率指数最低的为宁夏自治区为99.02%，最高的省份为天津市(105.44%)。全要素生产率指数是逐年上升的，每年最低的省份全要素生产率指数数值也逐渐增大，从横截面个体看，各个个体的全要素生产率指数也是上升的，这表明“十二五”时期我国碳排放全要素生产率指数是上升的。

综合上述现象，我们还发现全要素生产率指数的测算结果与各个地区的三种效率高低是一致的，特别是发达地区各年的全要素生产率指数都是处在上升的状态，并且是持续的上升，与效率呈现上升是一致的，中、西部的一些不发达地区效率较低，有些年份效率还出现了下降，这样导致全要素生产率指数也出现了下降的状况。

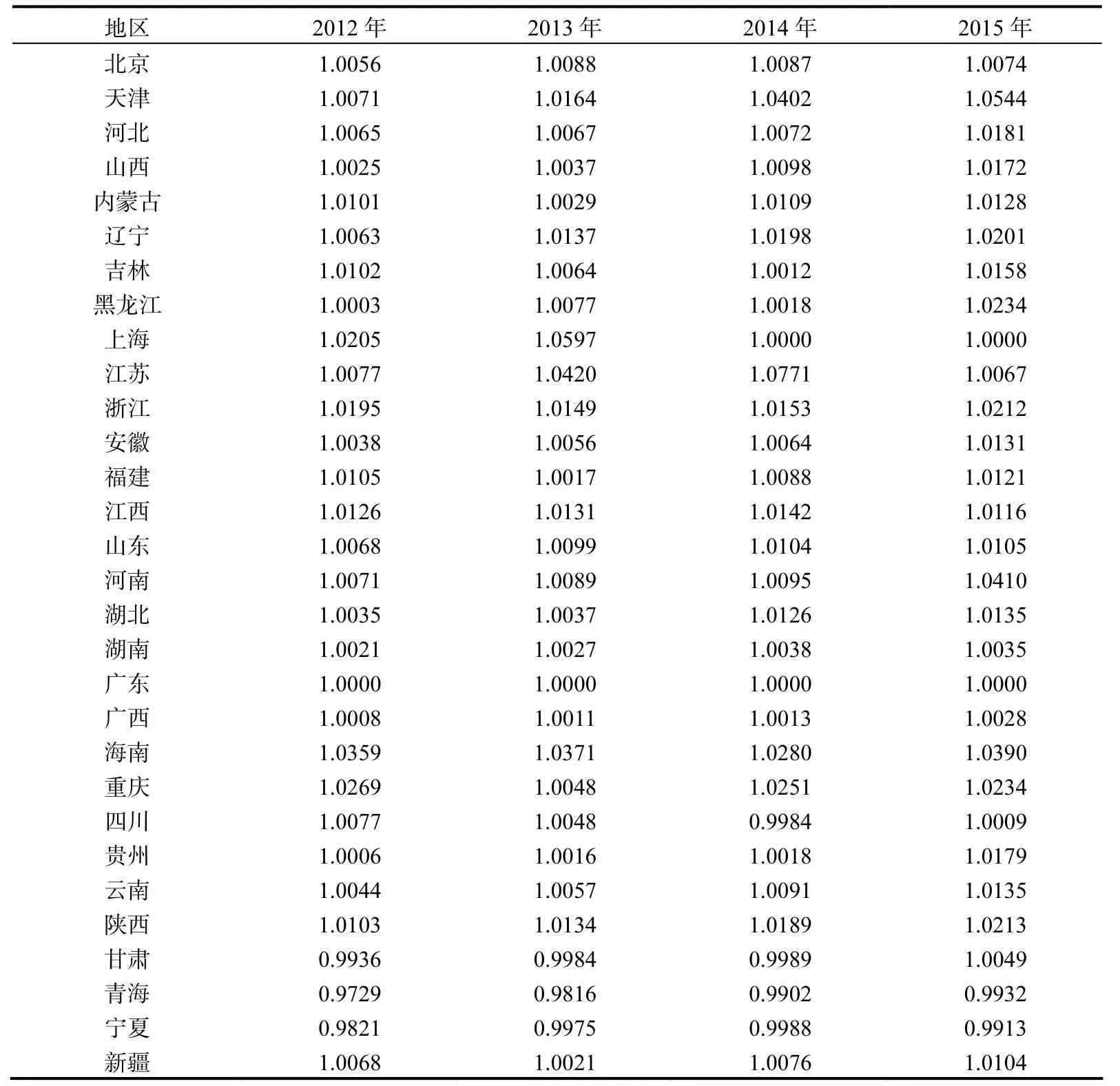
表4 2012—2015年各省份全局的全要素生产率

2.全局全要素生产率指数的分解

全局全要素生产率指数的分解，能够使我们看到全要素生产率指数中各个部分的贡献大小。根据全要素生产率指数的分解公式(8)我们可以得到全局 Malmquist-Luenberger全要素生产率指数分解项，包含技术效率改变项(EC)、离最佳实践缺口比率的改变项(BPC)、技术缺口比率改变项(TGC)数据。我们发现由于全要素生产率指数的变化较小，很多地区的全要素生产率指数接近1，所以分解导致这三个部分的大小变化不大。发达地区的技术效率始终都是超过1的，但是发达地区的离最佳实践缺口比率的改变项、技术缺口比率改变项会出现交替小于1的情况，表明发达地区的领导者地位会经常出现交替的变化，导致该发达地区离跨期的前沿面或者全局的前沿面距离发生变化，发达地区并不是所有时期数据都处在前沿面上，发达地区的各个省份处在前沿面地位是交替变换的，这也表明虽然各发达地区的效率是上升的，但是要想成为始终的领先地位还要继续努力。相反不发达地区的技术效率通常会小于1，这表明效率还有提升的空间，但是不发达地区的离最佳实践缺口比率的改变项、技术缺口比率改变项多数情况下是大于1的，这表明这些地区的效率虽低，但其追赶的速度是上升的，特别是西部地区的云南、陕西、甘肃、青海、宁夏、新疆，虽然效率小于1，但是其技术缺口的比率的缩小是明显的，这可能是由于发达地区的技术进步外溢，导致不发达地区的技术前沿也逐渐得到提高。技术效率表现的是管理经验、技术的使用状况，从上面的研究可以看出，不发达地区的技术效率提高得并非非常明显，所以今后不发达地区还是要努力提高技术效率，发挥效率这种第三生产率的作用，走节能减排的道路，最终提高生产率，为绿色发展贡献力量。

五、碳排放全要素生产率的影响因素分析

二氧化碳减排目标能否顺利实现，既有赖于国家宏观政策的制定，又依赖于相应的统计监测分析以及政策措施的实施。因此，从定性、定量角度研究影响我国二氧化碳排放的主要影响因素以及因素的贡献大小有着重要的意义。

本文将前面测算出来的全要素生产率指数采用计量回归分析的方法研究其影响因素，但是采用传统的方法时会出现一定的问题。Simar和Wilson(2007)认为采用基于数据包络分析得到的全要素生产率指数会存在着序列相关性，他们采用自助抽样法缓解这种相关性。Guan和 Lansink(2006)为了克服这种动态上的全要素生产率指数的前后相关性，对测量出的全要素生产率指数应用动态面板 GMM 估计方法进行影响因素分析。王兵和王丽(2010)同样采用动态面板数据模型对全要素生产率指数的影响因素进行分析。

考虑到全要素生产率指数的这种相关性特点，本文也采用该方法进行影响因素分析。首先，我们在模型中考虑了生产率指数的惯性，即包含了全要素生产率指数的滞后一期值，而动态面板数据能较好地处理这种滞后性问题。其次，实际上，人均产出高的地区全要素生产率指数也高，而动态面板数据模型能够较好地处理变量的内生性问题。在引入被解释变量的滞后一期值后，我们还需要其他影响因素的指标，例如，考虑了经济发展水平、外商直接投资等因素。我们在借鉴已有文献影响因素的基础上提出以下变量。

经济发展水平一般决定了一个地区的效率高低，经济发展水平高的地区通常对环境的要求高，环境控制得较为严格，我们采用不变价格的人均国内生产总值的对数(GDP)来表示，为了反映经济发展水平对产出的非线性影响，我们在影响因素中包含了经济发展水平的二次项(2GDP)。根据国际贸易理论外商直接投资会带来一个国家的环境效率变化，但是不同的实证研究的结论是不一致的，为此我们引入外商直接投资(FDI)这个变量。产业结构对环境的效率影响很大，工业产值比重过大，影响环境效率的提高，当然以工业中重工业或者高耗能行业增加值占国内生产总值的比重，来表示结构对效率的影响会更加明显，不过由于本文是宏观加总的数据，工业产值比重较高的省份也通常是重工业或者高耗能行业比较多的地区，因此我们将工业增加值占国内生产总值的比重表示产业结构(JG)。技术进步导致环境效率提升，技术进步我们用单位产出的能源消耗来表示(JSJB)，单位是吨标准煤/万元。最后一个变量是城镇化，城镇化对环境效率的影响是不确定的，我们用城镇人口占地区人口的比重来表示(CZH)。这些数据来自《中国统计年鉴》、《中国能源统计年鉴》各年。根据上述的指标我们建立的动态面板数据模型可以表示成式(10)：

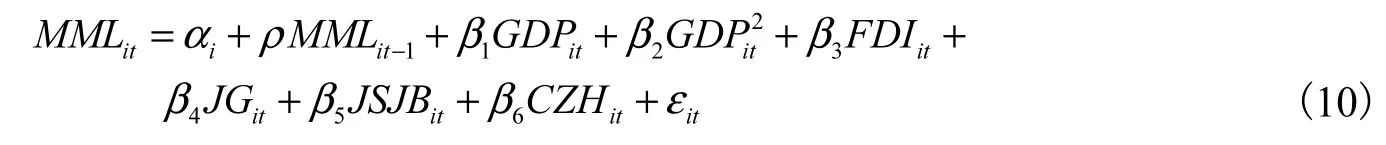
其中 MMLit表示各个省区各年的全要素生产率指数值，其他指标如上所述。由于模型右边有被解释变量的滞后一阶，应用普通的面板数据回归模型会导致有偏的结果，在实际中对动态面板数据常用的估计方法主要是广义矩(GMM)估计，其主要包含差分广义矩估计和系统广义矩估计。为了比较各种模型的结果差异，我们估计了6种模型，分别是 OLS估计、固定效应面板数据回归模型、一步和两步差分广义矩估计以及一步和两步系统广义矩估计，模型估计的结果见表5。

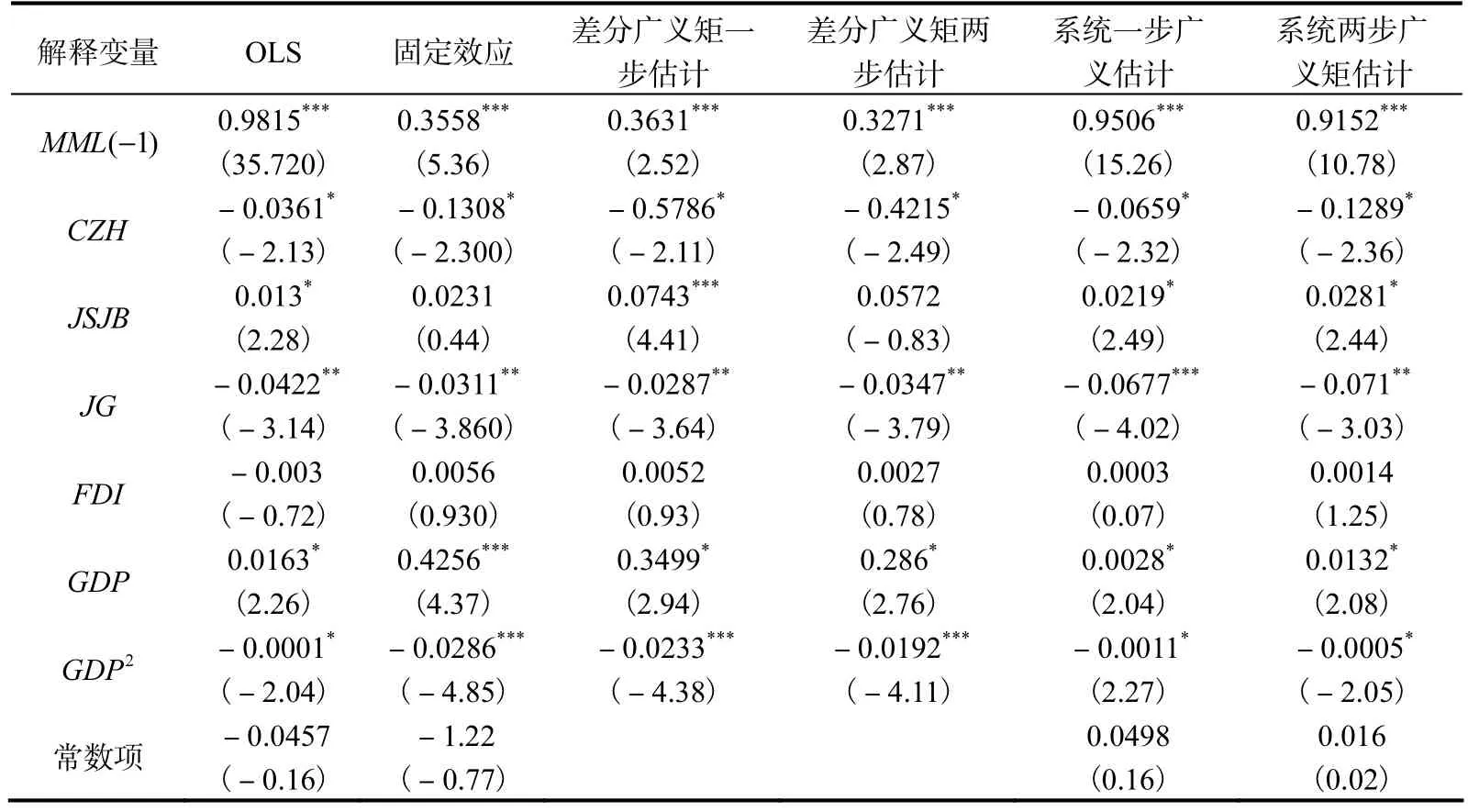
表5 全要素生产率指数影响因素的估计结果

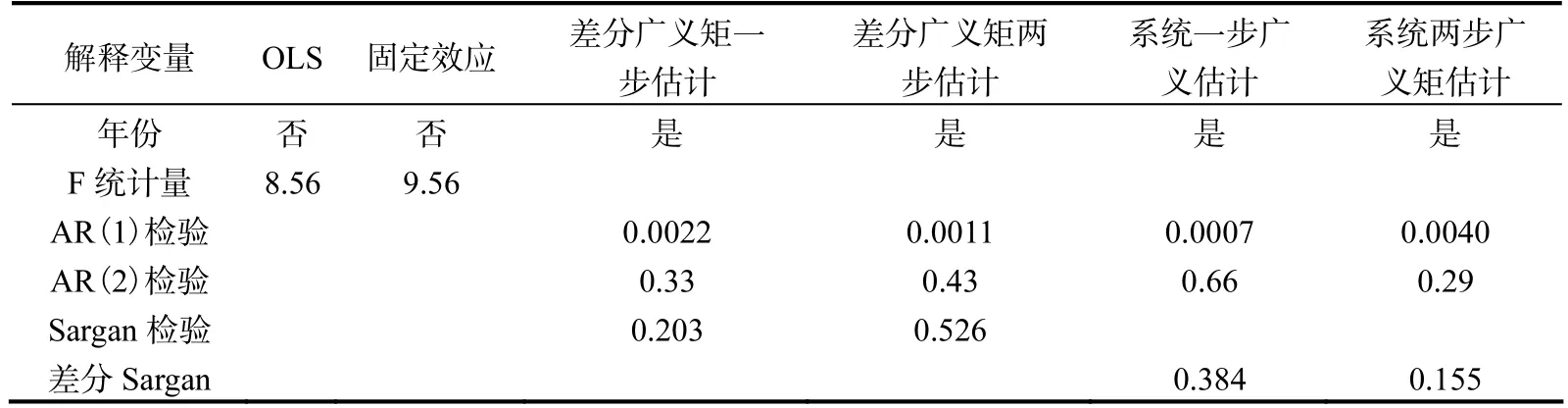
续表5

广义矩估计具有一致性的特点，但当样本容量较小或者使用较弱的工具变量时，动态面板广义矩估计容易产生很大的偏倚。Bond(2002)提出动态面板数据模型估计是否存在偏倚的方法，认为广义矩估计的结果应该在 OLS估计和固定效应估计的值之间，从我们模型估计的结果看，所有的广义矩估计结果均落在这两种估计值之间，估计的结果较好，没有存在较大的偏倚。

差分广义矩估计会导致一部分样本信息的损失，当解释变量在时间上具有持续性特点时，工具变量的有效性减弱，从而影响估计结果的渐进有效性，系统广义矩估计能够很好地解决上述问题，该方法同时利用了差分方程和水平方程的信息，水平方程中可以继续使用差分方程中用到的工具变量。检验工具变量是否有效的统计量是差分Sargan统计量，从检验的结果看，并不能拒绝新增工具变量是有效的假设，这表明系统广义矩估计是有效的。Sargan检验使用的前提是模型残差项εit符合一定的序列相关结构。从我们模型的估计结果看一阶不相关的假设被显著的拒绝，二阶不存在相关的假设不能被拒绝，说明残差项满足非序列相关的假定。差分广义矩估计和系统广义矩估计在方差结构复杂的情况下，两步估计优于一步估计，所以本文应用系统两步估计的结果进行分析。

从表5可以看出，环境全要素生产率指数的上期对下一期的影响比较大，上期环境全要素生产率指数的估计系数为0.9152，说明解释变量在时间上具有持续性特点，采用系统广义矩估计是合理的。城镇化对全要素生产率指数的影响在10%的显著性水平下显著，且系数是负的，表明城镇化不利于碳排放效率的提高，中国的城镇化会导致电力消耗和污染排放的增加，对全要素生产率指数起着下降的作用。技术进步在本文的研究中系数为正，技术进步导致排放的效率提高，全要素生产率指数的上升，未来应该继续加强节能减排技术的更新，降低单位产值的能源消耗，让技术成为提高全要素生产率指数的主要力量。经济结构变量对全要素生产率指数的作用为负，因为本文的结构变量用工业总产值占国内生产总值的比重表示，该指标上升表示经济结构逐渐重型化，这会导致碳排放全要素生产率指数的下降，且在1%的显著性水平下显著。经济发展水平对全要素生产率指数的贡献为正，这与多数文献的研究是一致的，一方面经济发展水平高，环境治理的技术也高；另一方面随着人们生活水平的提高，对环境的要求也越来越高，这两个因素共同作用导致效率的提升，同时本文还发现经济发展水平的二次方系数为负，且在10%的显著性水平下显著，这表明经济发展水平对提高效率的作用是非线性的，各省份的经济发展水平会影响到环境的效率，但是这种作用的效率是边际递减的。Grossman 和 Krueger(1995)认为外商直接投资对一个环境的改善存在着技术效应，在王兵和王丽(2010)的文献中验证了该结论，本文研究发现外商直接投资对全要素生产率指数影响为正但不显著。

六、结论和政策建议

本文通过基于改进的共同前沿模型，采用加权 Russell型距离函数，对各个地区的效率和全要素生产率指数进行计算，并对全要素生产率指数进行分解。通过计算我们发现，“十二五”时期的碳排放效率和全要素生产率呈现出全局效率、群组效率和同时期效率，在经济不发达地区和西部地区都较低，特别是宁夏自治区，其效率在各种测量方法下都是最低的，这与国家统计局公布的能源消耗强度的指标是吻合的。全局效率分析时绝大多数地区都存在非效率状况；跨期效率分析时，非效率的地区数量明显比全局效率分析中的地区少；同时期效率分析时存在非效率情况的地区更少，这主要是参考的前沿面地区越多时个体的效率变化越大，是共同前沿群组的异质性导致的。根据共同前沿模型的特点，我们还发现各地区存在着全局效率小于跨期效率，跨期效率小于同时期效率的现象，这进一步说明采用共同前沿模型分析效率是必要的。

根据上述的效率数据，本文又计算了共同前沿 Malmquist-Luenberger 全要素生产率指数，计算结果表明效率高的地区，全要素生产率指数也较高，但是全要素生产率指数的数值都较小；对全要素生产率指数进行分解，发现技术进步较为明显，表现在跨期的前沿面和全局的前沿面不断的缩小，技术效率有待提高。

最后，本文选取了影响全要素生产率指数的各种因素，应用动态面板数据对全要素生产率指数的影响因素进行分析，研究发现经济发展水平对全要素生产率指数有着积极的作用，但是这种作用的边际效应是递减的，经济结构重型化不利于技术效率和全要素生产率指数的提高，用能源消耗强度表示的技术进步始终对全要素生产率指数起着积极的作用，城镇化不利于全要素生产率指数的上升，城镇化导致能源消耗增加，从某种程度上对环境的影响比农村要大，上述指标对全要素生产率指数都有不同的影响，而且比较显著；但是本文发现外商直接投资对全要素生产率指数的作用为正，但不显著，这与有些文献认为有积极或者消极作用的结论明显不同。上述结论的出现可能与已有的研究有区别，一个方面取决于效率变化的范围大小，即数据的变化范围越大，影响因素分析的计量结果可能越合理；另一方面是数据的研究区间长短会影响计量结果，所以未来的研究方向应该是更加准确的原始数据和更长的研究时间。