基于改进掩膜EMD的光纤陀螺振动信号处理方法

王 威 陈熙源

(东南大学仪器科学与工程学院， 南京 210096)

光纤陀螺是一种基于Sagnac效应的角速度传感器[1].振动会引起光纤陀螺的非互易相移，是光纤陀螺的主要误差源之一[2]，这制约了陀螺的精度和应用，因此有必要对光纤陀螺的振动机理和信号处理进行研究.

陀螺的振动处理方法可分为硬件方法和软件方法.硬件处理方式旨在减少振动的干扰，主要有以下方法：① 通过在光纤陀螺内部增加减震装置，隔离或减小外界振动对于光纤和光学器件的影响[3]；② 通过对光纤陀螺内部的光纤环进行固胶处理或者优化光纤环的层数和安装方法，降低振动对于应变产生的影响，从而缓解振动对陀螺的影响[4]；③ 通过改进光纤陀螺的机械结构，降低外界振动对内部光纤环路和光器件的影响[5]；④ 通过对光纤环进行改进，如改造成多极对称绕法，使得振动对于光纤环产生的非互易相移互相抵消，从而间接地消除振动的影响[6].硬件方法会带来体积、成本、功耗增加和结构复杂等缺点，这与陀螺小型化和低功耗化的发展趋势相悖.相比硬件处理方法，软件处理方法灵活性高，不会增加硬件成本、质量和体积.常见的振动误差软件处理方法有：① 利用小波分解和重构滤波方法对车辆振动环境中的IMU(inertial measurement unit)输出信号进行滤波[7]，从而消除振动和噪声；② 在分析了振动对陀螺光路影响的前提下，采用最小均方滤波算法去除光路中特征频率的振动噪声等[8]；③ 采用经验模态分解EMD及其改进算法对振动信号进行分解或滤波，进而进行建模和补偿[9].上述文献仅对静基座或者振动信号较单一的情况进行了研究，但是SINS的使用环境非常复杂，单一的模型不能准确表征陀螺所处的振动环境.

本文基于改进的掩膜EMD[10]，提升陀螺振动信号的分解效果.分析得到掩膜的最佳频率后，通过粒子群算法(PSO)[11]对掩膜信号的幅值进行寻优，然后根据得到的频率和幅值构造掩膜信号.对分解后的多尺度振动信号和原信号之间求取相关系数，据此分离出噪声和振动信号.最后，将支持向量机(SVM)[12]作为建模算法，历史振动信号作为模型的参数，以预测的方式达到实时处理的目的.

1 光纤陀螺的振动分析

振动对于光纤陀螺输出的影响主要有2个方面:① 振动引起光纤长度和折射率的改变，进而影响陀螺的输出[13]; ②振动引起光路的光功率的变化.根据光弹效应可知，振动应力会引起光纤环的形状改变，进而造成光纤折射率和长度的变化.当光纤长度和折射率发生改变时，光经过振动点时的相位将发生改变，这种改变将导致光干涉强度的变化，进而影响光纤陀螺的输出.而光强的改变则直接影响干涉的效果，根据Sagnac原理可知，光纤陀螺的输出也随之而变.一般而言，振动以正弦波的形式在光路中传播，其引起的非互易相移可表示为[13]

φv=φ(f)cos(ωt+θ1)

(1)

式中，φv为振动引起的非互易相移；f为振动频率；φ(f)为非互易相移的幅度；ω为振动角频率；θ1为振动信号的初始相位.光纤陀螺的原理是通过检测顺时针和逆时针2束光之间的干涉强度，进而判断载体的转速.因此，振动引起的光路中光功率的变化不可忽视，它是引起陀螺输出误差的根本原因.振动引起的光功率变化可表示为

P=P0[1+ΔP(f)cos(ωt+θ2)]

(2)

式中，P为振动环境下的陀螺输出光功率；P0为光源的平均功率幅值；ΔP(f)为振动引起的附加光功率的幅度；θ2为附加光功率的初始相位.结合式(1)、(2)和Sagnac的检测原理，可得到振动环境下光纤陀螺输出的干涉信号表达式：

I=-4KP0[1+ΔP(f)cos(ωt+θ2)]·
sin[Δφ+φ(f)cos(ωt+θ1)]sinφ

(3)

式中，I为干涉信号；K为系统增益；Δφ为系统调制相移；φ为偏置调制相移；P0为光源的平均功率幅值.从光纤陀螺的输出形式来看，振动造成的光纤陀螺输出的改变以正弦波和余弦波为主.

2 改进的掩膜EMD

当2个混叠频率接近时(介于2倍频之间)，传统基于噪声辅助的EMD算法往往不能有效地分离出混叠信号，工程适用性受到限制.掩膜EMD[10]是一种基于正弦信号辅助的经验模态分解算法，能够较好地解决EMD类算法中存在的模态混叠问题.但传统掩膜EMD在使用时存在频率偏低和幅值无法确定的问题，分解效果不理想.传统EMD算法如下：

(4)

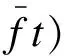
(5)

式中，a1(i)为Hilbert变换后的瞬时幅值；f1(i)为瞬时频率；k为信号长度.由式(5)可知，传统掩膜EMD的掩膜信号的频率是基于幅值的一种加权平均.当混叠信号的成分多于2个时，由式(5)所确定的掩膜频率要小于混叠信号的最高频率成分.在实际使用时，这样偏低的频率不能得到理想的分解效果.为了说明掩膜信号频率对分解的效果，考虑下面的混合信号：

(6)

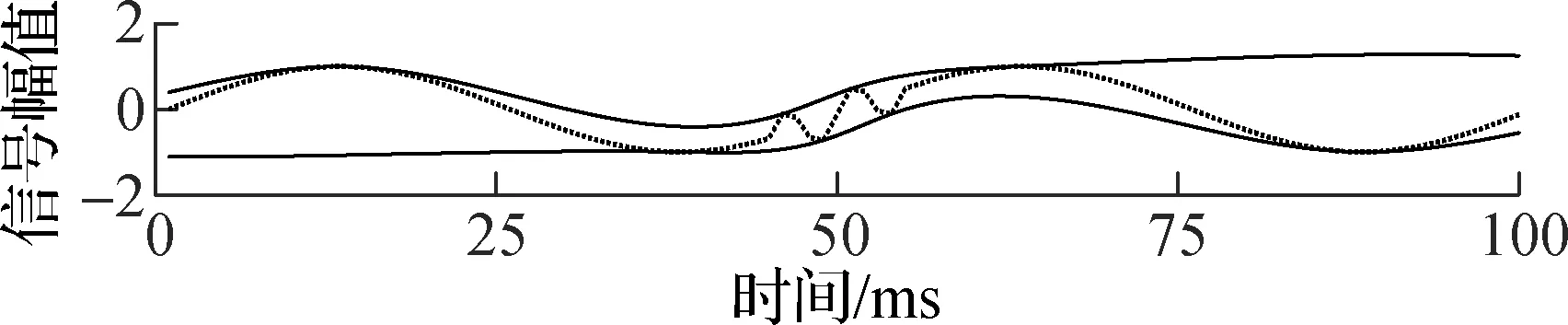
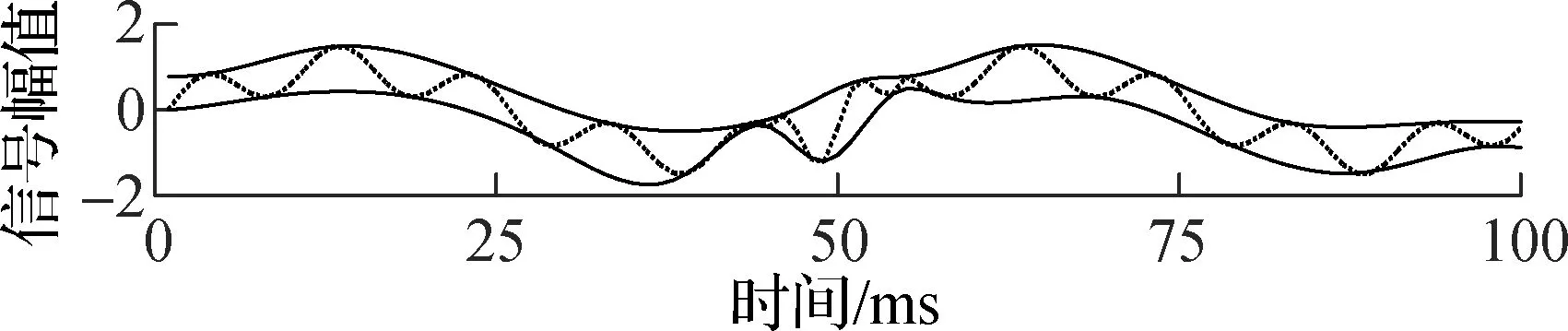
式中，f1=200 Hz,f2=20 Hz,0.060 s≤t1≤0.070 s， 0 s≤t2≤0.099 s. 正弦掩膜信号定义为asin(2πfmaskt2)，其中fmask为试验掩膜信号的频率，分别设置为100, 200, 400 Hz，a设置为0.5.把式(6)的信号和掩膜信号代入式(4)进行掩膜EMD分解，得到的包络图如图1所示.

(a) 原信号包络

(b) fmask=100 Hz包络

(c) fmask=200 Hz包络

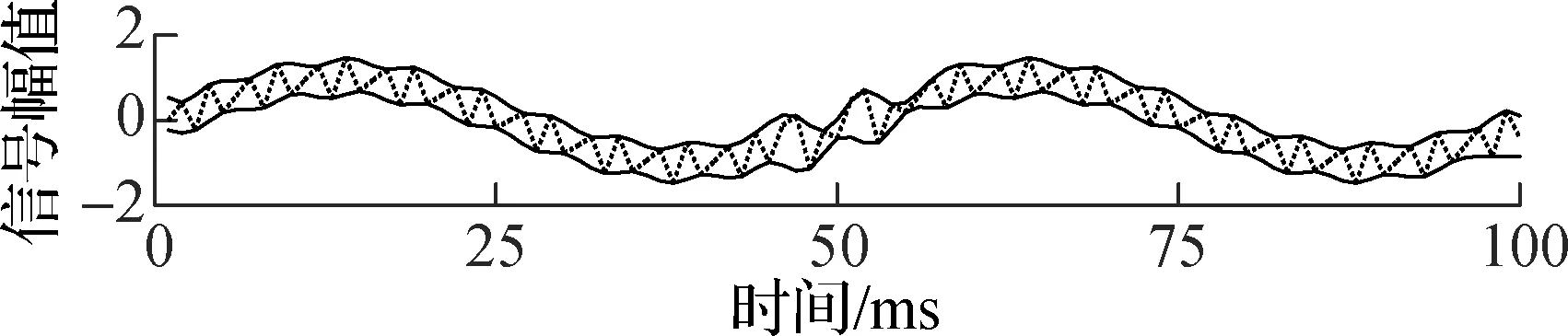
(d) fmask=400 Hz包络

由图1可见，原始信号的上下包络没有反映出混合信号的低频成分x2(t2)的形状，此时传统EMD分解不能将混合信号分离.当掩膜信号频率为100和400 Hz时，包络曲线存在局部缺陷，会影响到低频信号的提取，而频率为200 Hz时的包络则较好地反映了低频成分的信号形状.分别提取图1各个包络的中心线，并与低频信号x2(t2)进行对比，如图2所示.

(a) 原信号包络中心线

(b) fmask=100 Hz包络中心线

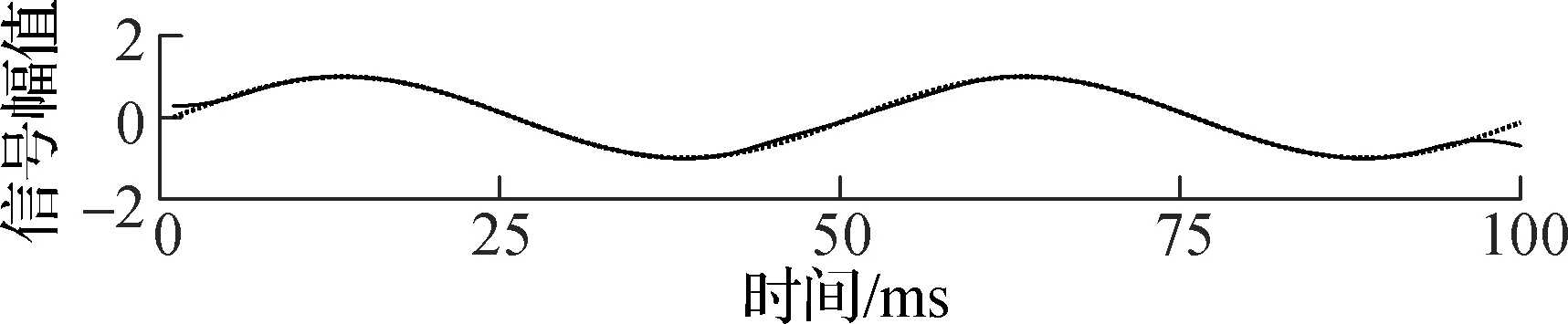
(c) fmask=200 Hz包络中心线

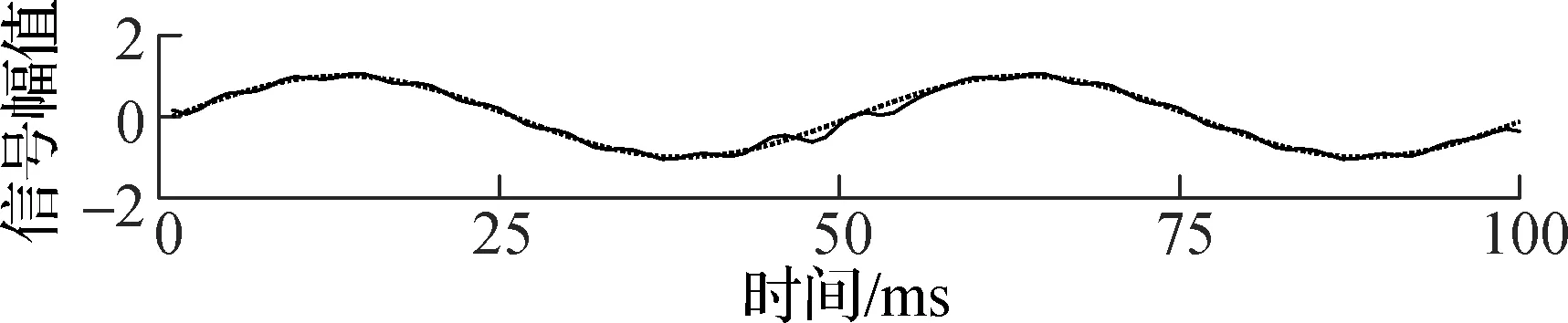
(d) fmask=400 Hz包络中心线

图2包络中心线与低频信号的比较

由图2可见，当掩膜频率等于200 Hz时分解的效果最好，而200 Hz正是混合信号中高频成分x1(t1)的频率.不失一般性，取间隔频率Δf=50 Hz，且简化频率信号为x2(t2)=0，分别取间隔频率的整数倍作为掩膜信号的频率进行分解，其中心线簇如图3所示.

图3 等间距掩膜频率下的中心线

(7)

Amask∈[0.01σ,σ]

(8)

式中，σ为待分解信号的标准差.具体选择掩膜信号幅值时，以0.01σ为步长，在式(8)的范围内采用粒子群进行寻优.改进的掩膜EMD主要步骤如下：

① 使用EMD循环对IMF1进行分解，直到分解模态分量的个数为1.

② 对最终的IMF1求取功率谱，通过功率均值阀值滤波，得到满足阀值的最高频率，以此作为掩膜信号的频率，如式(7)所示.

③ 在设定的幅值范围内，以0.01σ步长进行寻优.

④ 得到掩膜信号的频率和幅值后，构造掩膜信号

(9)

⑤ 把掩膜信号代入式(4)，得到各个IMF.

为了描述方便，将本文改进算法称为自适应掩膜EMD(AMEMD).为了验证算法的有效性，构造混合信号如下：

(10)

式中，f1=150 Hz,f2=90 Hz,0 s≤t≤0.499 s.分别采用集合经验模态分解(EEMD)算法、完备总体经验模态分解(CEEMD)算法和本文的改进AMEMD算法进行对比实验，分解结果如图4所示.

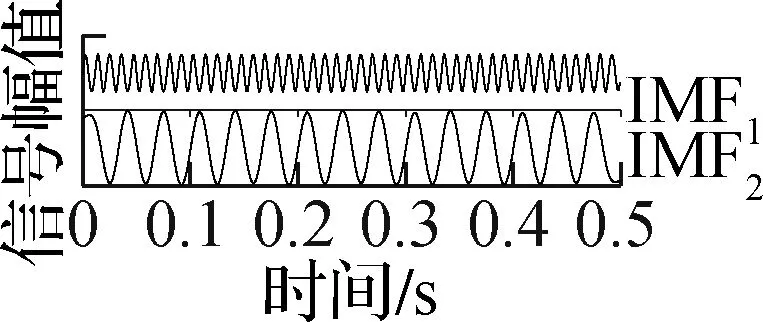
(a) AMEMD

(b) EEMD

由图4可见，AMEMD算法成功地把2个频率成分接近的混合信号分离开，而EEMD和CEEMD算法则发生了明显的混叠，并且产生了较多的虚假模态成分.

3 陀螺振动信号的实时处理方法

首先通过改进掩膜EMD算法从振动基座陀螺输出信号中提取出振动周期信号，然后通过支持向量机(SVM)对振动信号进行建模，利用历史振动信号对当前时刻振动信号进行预测，以此达到实时消除振动影响的目的.陀螺振动信号的处理算法如图5所示.

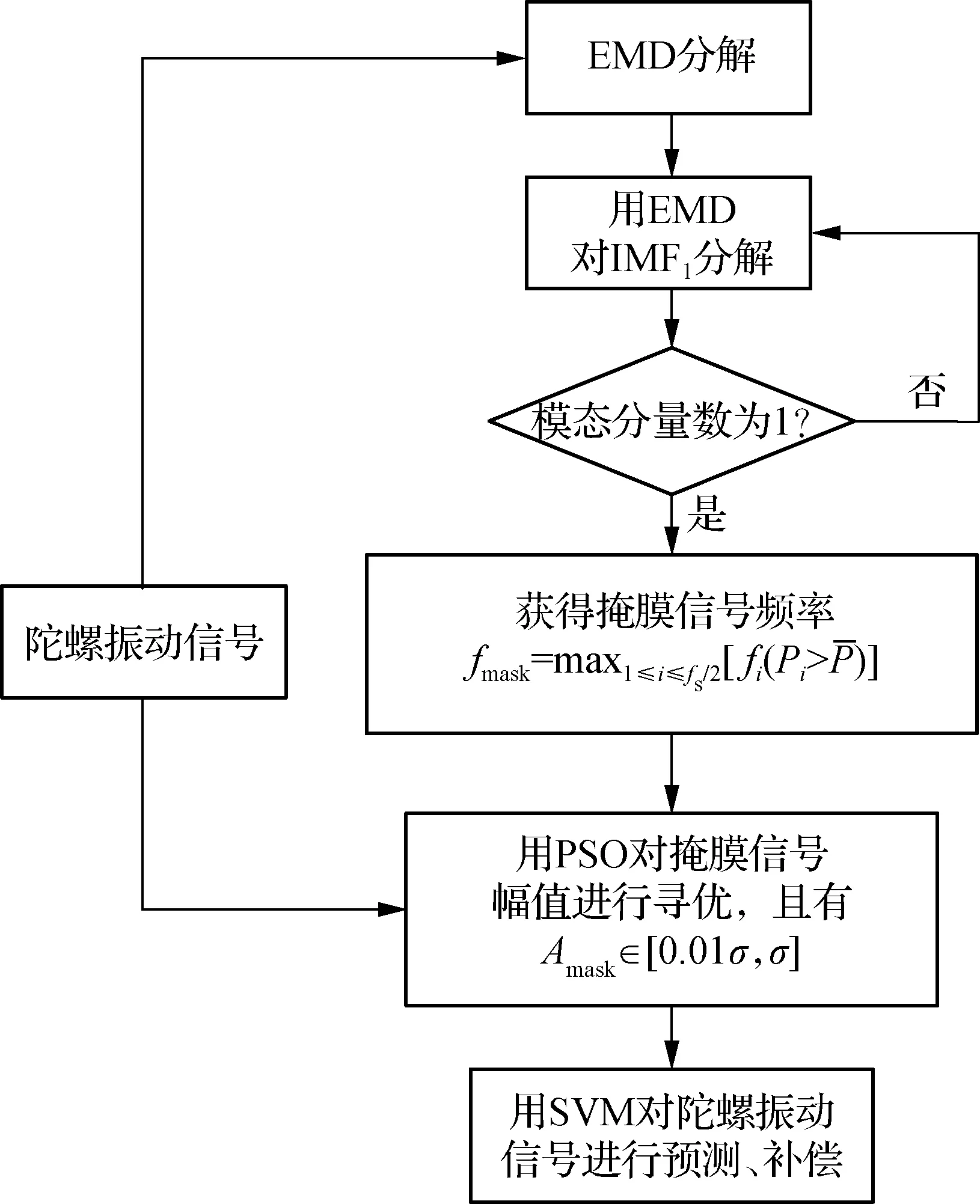
图5 陀螺振动信号实时处理流程图

4 结果和讨论

在实验室用振动台模拟对光纤陀螺的角振动，振动频率设置为2 Hz，采样频率设为1 kHz，实验用光纤陀螺的零偏精度为0.1°左右.由于采样数据有较多误差，按照工程中常用的均值滤波进行数据预处理，均值滤波窗口长度设置为70，原始数据和滤波后的数据如图6所示.

(a) 陀螺原始输出

(b) 陀螺滤波输出

分别采用EEMD算法、CEEMD算法和本文的改进AMEMD算法对图5中的角振动数据进行分解.分解结果如图7所示.

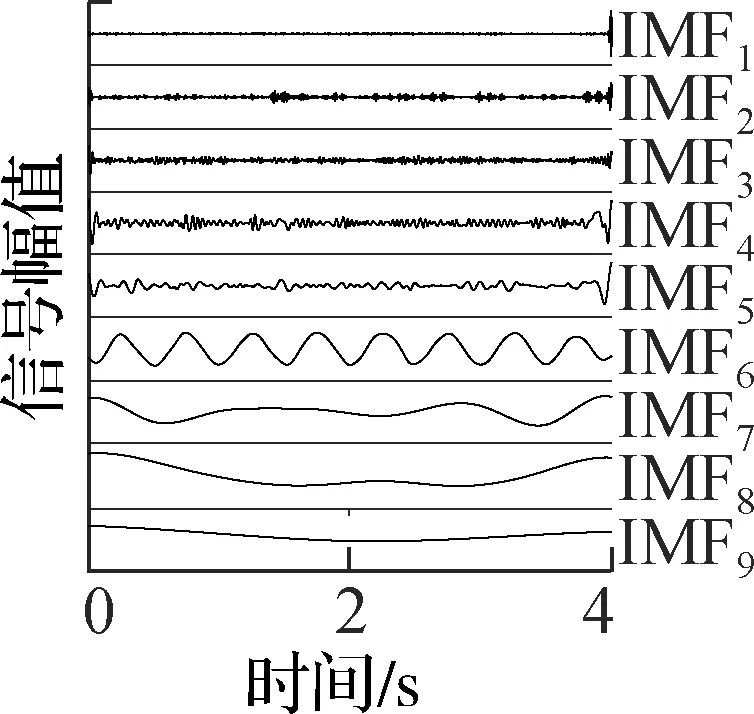
(a) AMEMD

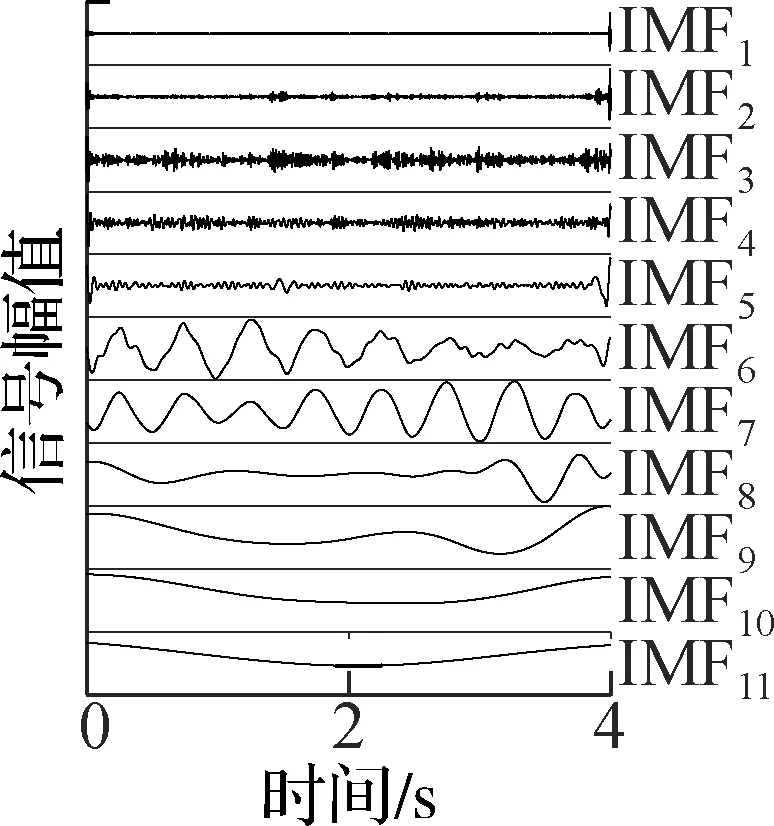
(b) EEMD

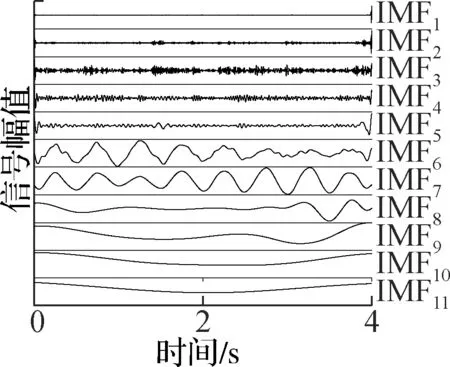
由图7可见，AMEMD算法分解出了单频的角振动信号，而EEMD和CEEMD算法则产生了明显的混叠.另外AMEMD算法分解的IMF最少，同频信号较为集中.为了详细比较各种算法分解的效果，分别对上述3种分解结果的IMF进行频谱分析，以此判断分解的效果.3种算法的频谱分别如图8～图10所示，为便于查看，把低频IMF带宽减小到20 Hz.

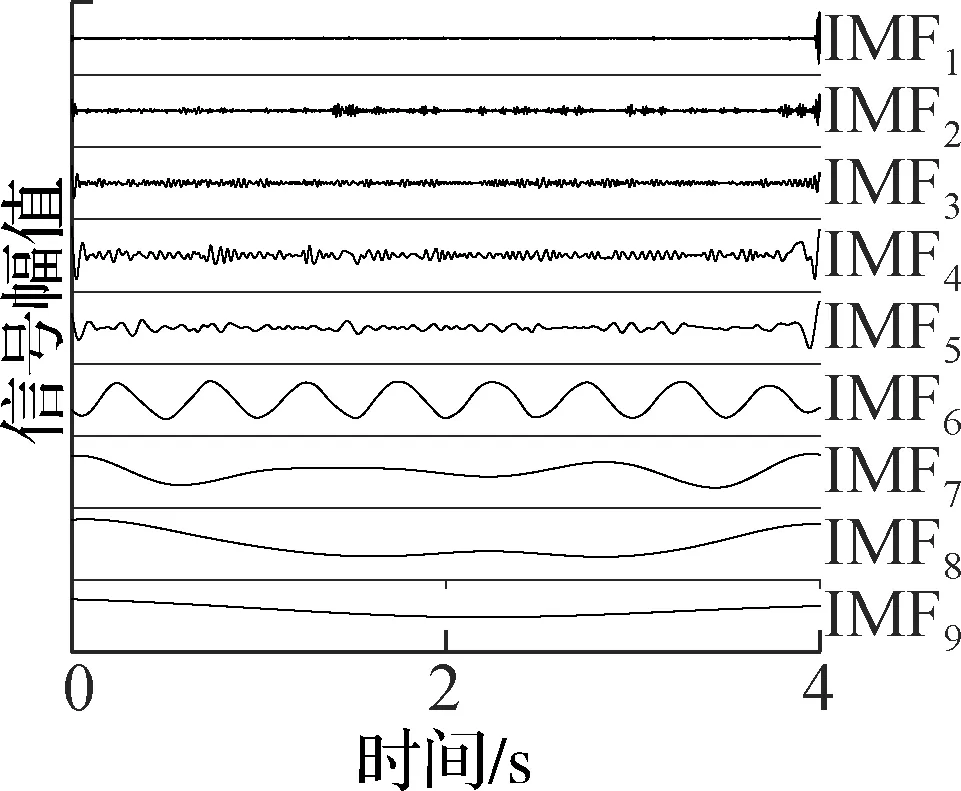
(a) 分解图

(a) 分解图

(a) 分解图

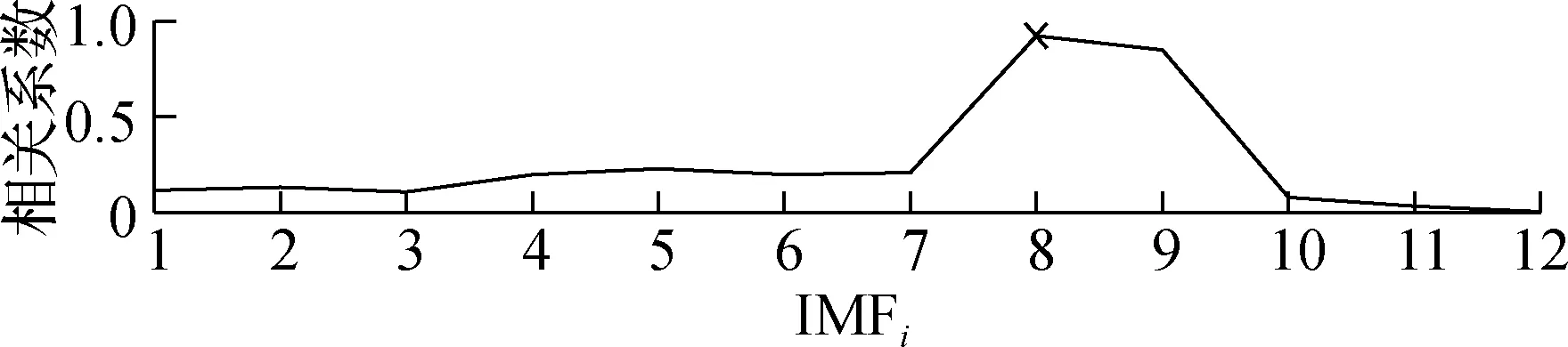
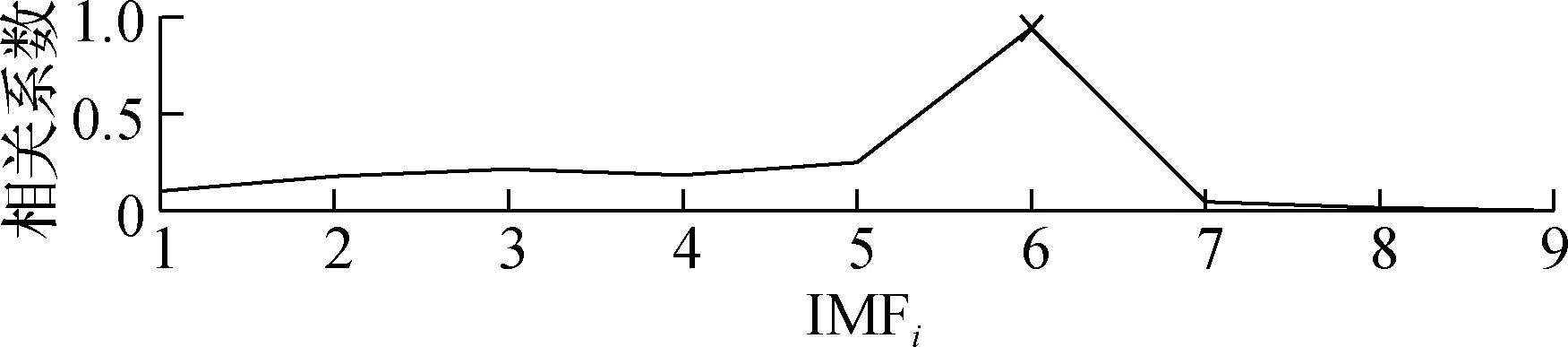
通过对比图8～图10的频谱图可知，AMEMD算法完整地分离出了2 Hz的角振动信号，和其他IMF并没有发生模态混叠.而EEMD算法的IMF6和IMF7之间发生了明显的模态混叠；CEEMD算法则在IMF8和IMF9之间发生了明显的模态混叠.为了提取出振动信号，分别对各个IMF和原始陀螺输出的均值滤波信号求取相关系数，为了保证有用信号不会被当作振动信号而提取、补偿掉，把相关系数最大的IMF作为振动信号，高频IMF作为噪声；而低频IMF作为陀螺振动补偿后的输出.分别对上述3种算法的IMF和图6(b)的信号间求相关系数，结果如图11所示.

图11中的叉号表示相关系数的最大值，相对应的IMF即为振动信号.由图可见,AMEMD算法只有1个峰值，而EEMD和CEEMD算法则有2个明显的峰值，这正是由模态混叠造成的.分别以相关系数峰值对应的IMF作为振动信号，其结果如图12所示.

(a) EEMD

(b) CEEMD

(c) AMEMD

(a) EEMD

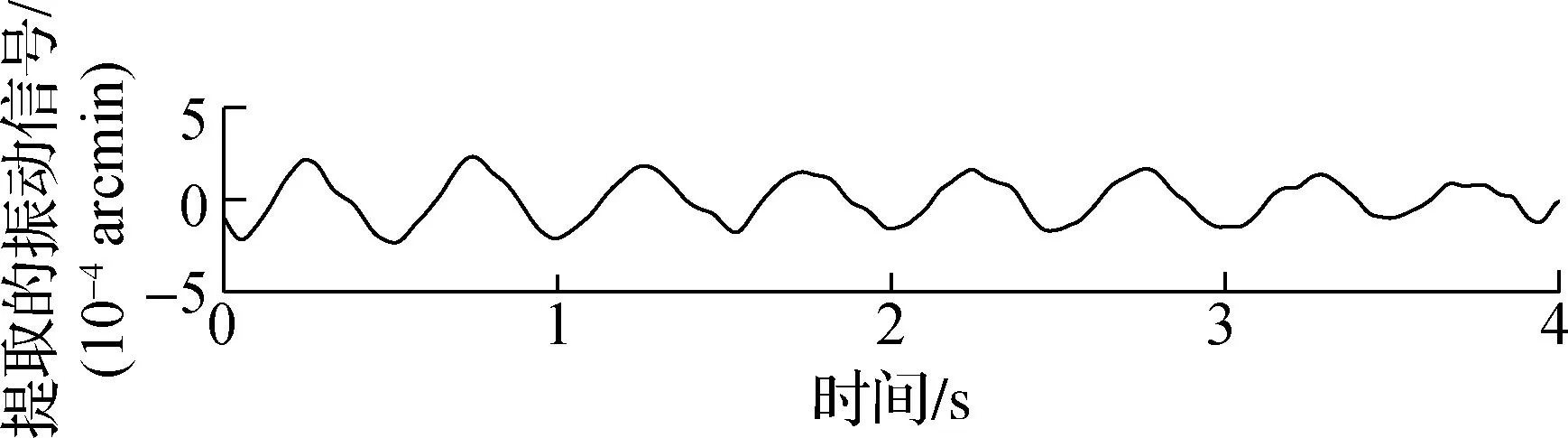
(b) CEEMD

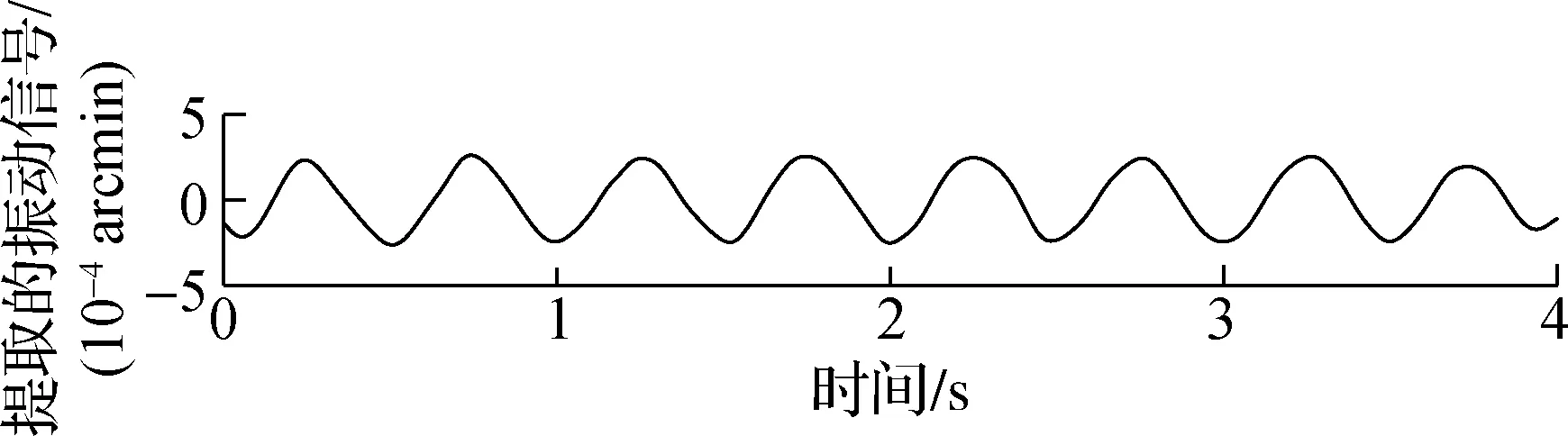
(c) AMEMD

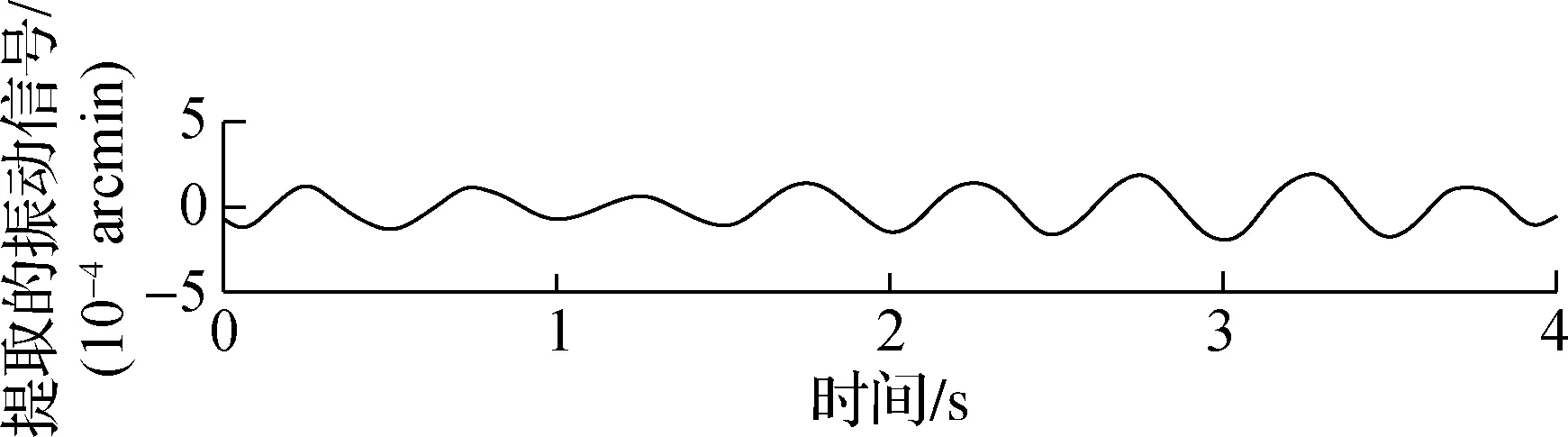
由图12可见，AMEMD算法得到的振动信号最完整，EEMD和CEEMD算法提取的振动信号则出现了不同程度的幅度波动.对以上提取信号分别和图6(b)的滤波后的振动信号求取相关系数，EEMD算法、CEEMD算法和AMEMD算法对应的相关系数分别为0.905 6，0.923 3和0.940 7，由此可见，AMEMD算法具有最好的分解结果，能够有效地提取出陀螺振动信号.

为了对振动信号进行补偿，需要对振动进行建模.陀螺振动是由载体动力部件或者结构谐振引起的，有着相对固定的振动频率，因此本文对图12(c)提取的振动信号按照时间序列进行建模.将支持向量机(SVM)作为建模算法，历史振动信号作为模型的参数，则第i个振动信号的预测模型为

(11)

式中，d(i)为第i时刻的振动预测结果；d(i-k)，d(i-k+1)，…，d(i-1)分别为第i-k，i-k+1，…，i-1时刻的历史振动数据，其中k为不小于1的正整数.为得到最好的预测效果，同时考虑到计算效率，取k≤20，并在此范围内寻优，并对预测的结果和图12(c)提取的振动信号求取标准差，其误差结果如图13所示.

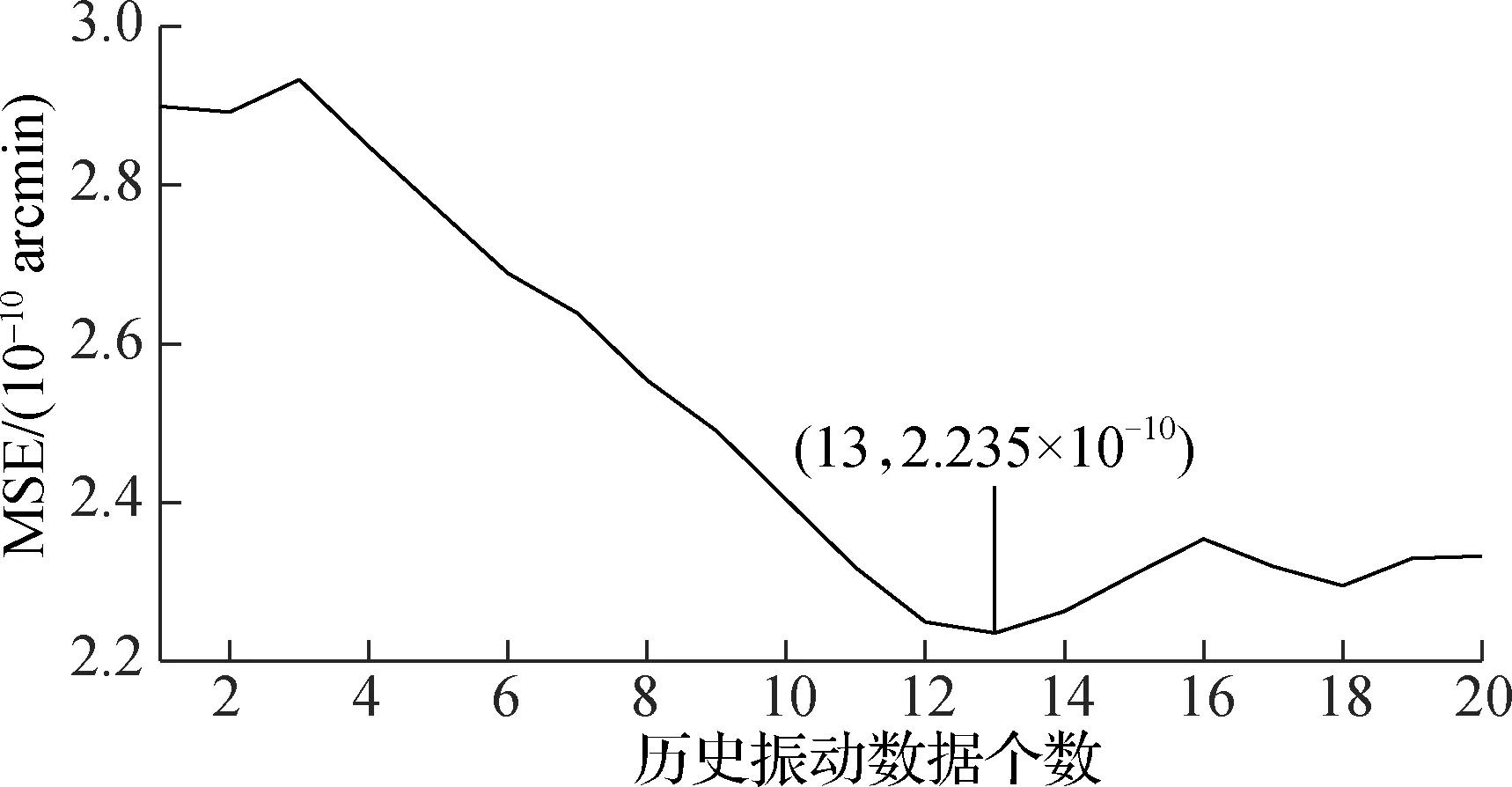
图13 陀螺预测误差图

由图13可见，当历史数据个数为13时，振动预测的误差最小.对陀螺原始信号与陀螺振动预测值作差，即可得到补偿后的陀螺输出信号.用Allan方差[14]分别分析原始信号和补偿后的陀螺输出信号，结果如表1所示，其中Q为量化噪声系数，N为角度随机游走系数，B为零偏不稳定性系数，R为速率斜坡系数，K为速率随机游走系数.

由表1可见，改进的AMEMD算法具有低的噪声系数，较原始信号的噪声在B，R和K等指标上有1个数量级以上的改进.该算法不但能够有效地提取振动信号，而且能够同时达到实时补偿的效果.

表1 陀螺输出的Allan方差分析

5 结论

1) 掩膜信号的频率值是影响掩膜EMD分解效果的主要因素，掩膜信号的最优频率值等于混合信号中高频分量的频率值.基于最优掩膜频率和幅值寻优策略的改进掩膜EMD算法能够有效地提取光纤陀螺振动信号.

2) 对于周期性的光纤陀螺振动信号，以历史振动信号作为模型建模参数，通过支持向量机对陀螺振动进行建模和预测，可以实现陀螺振动信号的实时补偿.

3) 为了建立精确的模型，需要对历史振动信号个数进行寻优.通过建立振动信号个数和模型误差之间的关系，进而确定模型参数的最优数量.