基于广义S变换能量值信息熵加权的DG电网故障判断研究

，，

(三峡大学电气与新能源学院,湖北 宜昌 443002)

1 引言

分布式发电技术的蓬勃发展，使得分布式电源(Distributed Generation，DG)的并网容量日益提高，而DG的并网运行不仅改变了传统电网络的结构，且因其自身结构及调节机理导致电网故障时暂态特征发生变化，因此对电网的运行的控制、保护的配置和故障的判断等产生了巨大影响[1-7]。

文献[8]提出在微电网孤岛运行条件下，发生故障时，根据PWM调制系数是否越线，将DG等效为恒压源或其与阻抗串联的模型，其阻抗大小为滤波器等值阻抗。文献[9]则提出将DG等效为恒压源和恒定阻抗串联，通过等值阻抗压降和系统电压求DG的等值电动势，但此方法会因DG并网方式和控制策略不同而存在一定的局限性。文献[10]将DG作为节点，根据配电网中各元件的及连接方式，建立配电网系统模型，采用迭代式补偿电流法求解配电网负荷模型的短路电流和短路电压，构造同伦方程，利用计算的短路电压值和电流值构建导纳矩阵，求解、更新导纳矩阵,得到收敛短路电流解，但此方法计算量太大，不利于大面积网络分析。文献[11]将DG看作不同类型的节点，提出了含分布式电源的三相不平衡配电网故障计算的改进前推回推算法，但未考虑DG的不同控制策略的影响。

文献[12]通过推导DG的等效正、负序突变量阻抗解析表达式，分析不同控制策略、故障条件和负荷电流下等效序突变量阻抗角的变化规律，进而揭示出DG对各类故障分量方向元件的影响机理。文献[13]通过比较同一母线上的故障线路与其余馈线的正序电流故障分量，分析了含DG网络中故障分量幅值和相位，得出了故障分量在含DG网络中同样适用的结论。以往的故障判断多采用工频量的序分量法和突变量法[14],其中突变量法具有动作速度快的优点，但其适用范围有限，易受保护装置安装位置和故障类别影响，可靠性不足。序分量法虽能填补突变量法的缺点，但此方法需要的故障信息量较多，通常要提取故障后全周波的数据，降低了判断速度。文献[15]利用稳定存在于故障行波中的行波固有频率成分并将其与原子分解算法结合，计算故障信号各频率成分的原子能量熵，最后利用最大能量熵值判断出故障类型。文献[16]利用故障后一段时间内故障电压和故障电流的S变换能量相对熵表征极性关系,进而根据线路两端S变换能量相对熵的比值来识别区内外故障。

基于此，本文提出通过比较信息熵加权的广义S变换能量值的方法来进行故障判断，不仅能利用故障后极短时间内对数据进行故障判别，而且不受故障角与过渡电阻的影响，大大提升了判断的可靠性,通过PSCAD建立DG并网模型仿真验证了该方法的可行性。

2 广义S变换原理

2.1 故障分量提取

故障分量是只有在系统发生故障时才出现的电气量，是故障信息在电气量上的具体体现。根据叠加原理，故障状态可由非故障状态与故障附加状态叠加而成。

根据叠加定理，以m端为例，有：

(1)

故障分量的提取

Δi(k)=i(k)-ipre(k)=i(k)-i(k-nN)

(2)

式中：N表示一个周波的采样点数；Δi(k)表示当前采样时刻的故障分量，i(k)表示当前采样电流；ipre(k)表示当前采样时的正常电流。由于系统频率的波动，n一般不能取过大。

2.2 广义S变换原理

S变换是由地球物理学家R.G.Stockwell于1996年提出的一种加时窗的时频可逆分析方法，可看成是短时傅里叶变换(STFT)演变得到，也可看成是小波变换(CWT)的相位修正，具有短时傅里叶变换的单频率独立分析与小波变换多分辨率分析的优点。

时间信号h(t)的S变换可定义为:

(3)

令p(t,f)=h(t)e-j2πft则有：

(4)

式中：t为时间；τ为控制高斯窗在时间轴位置的参数；f为频率。

故设h(t)的离散时间序列为h[kT](k=1,2,3…N-1)，T为时域采样间隔，则h[kT]的离散S变换为：

(5)

由上式可以看出该变换运用了频移，通过频谱H[(m+n)/NT]围绕着中心频谱n进行平移，使S变换的基函数具有正交性，并能表示该空间所有集合，即此基函数具有完备正交性。

若将高斯窗定义为:

(6)

(7)

由式(7)可知时间窗宽度的尺度因子σ是关于频率的函数，故具备了在时频平面上随f变化而自适应调节时窗的能力，增强的S变换的分辨率，称之为广义S变换。其表达式为：

(8)

可以看出S变换是广义S变换的特例。广义S变换后的结果是二维复数矩阵，可以得到幅值跟相位，其中行代表采样时间，列表示对应的离散频率。因此利用广义S变换分解出任一频率的行波随时间变化的分布。离散数据经广义S变换后的结果，将得到复时频矩阵S，此S矩阵某位置上元素的大小就是相应频率和时间处信号经广义S变换后的幅值，其列向量为某一时刻随频率变换的分布，行向量为某一频率随时间变化的分布，第一行对应信号直流分量，其余行相邻间的频率差为Δf=fs/N，其中fs为采样频率，N为采样点数。表达式为：

(9)

其中，m，n分别表示所对应的行与列，即特定是频率和时间。

2.3 故障过程暂态能量分析

对于电流信号h(t)，定义其信号总能量为在1Ω电阻上消耗的能量，即：

(10)

根据Parseval定理，一个信号所含有的能量恒等于此信号在完备正交函数集中各分量能量之和。信号能量即能在时域中求得，也可以从频域中求得。由上文可知S的基函数是完备正交的，因此满足Parseval定理。可得出能量在频域表达式为：

(11)

S矩阵中的数值表示广义S变换后在该频率和时间点下的幅值大小，根据Parseval定理，定义经S变换后的复矩阵的能量矩阵为E，其中E(m，n)=[S(m，n)]2。显然对矩阵E进行行积分可得到信号能量在频率分量中的分布，列积分得到信号能量在时间上的分布，因此可从E矩阵中得出特定频率与时间段中的能量，从而可定义故障后的S暂态能量为：

(12)

根据上式可得故障发生后短时间内特定频率的能量大小，从而可对故障后的一段时间内的故障信号进行评估。该信息不仅反应了电流频率空间内能量的分布信息，包含了暂态信号的特征，可作为故障选相分析的参考量。

2.4 信息熵的权值

熵是德国物理学家学家鲁道夫·克劳修斯于1850年提出的，并应用在热力学中，表示一种能量在空间中分布的均匀程度，能量分布得越均匀熵就越大。事物的不确定性可用信息熵表示，数据越有序，信息熵越低，反之，如果数据越混乱，信息熵则越高。

对于一个离散随机变量X，其定义空间为一个字符集E，相应的概率分布函数可用pi(x)表示，pi(x)=p(X=x)，(x∈E)，则各信息成员提供信息的概率计算式如下：

(13)

根据信息论，计算离散随机变量的熵Wi为：

(14)

则信息熵加权系数wi为:

(15)

信息熵加权系数可体现不同属性下所包含的信息量大小，对广义S变换能量进行加权计算可反映不同频率的能量值在其中的作用，同时能自适应调整各频率能量所占比重，可增加计算结果的可靠性。根据式(16)可知故障发生后短时间内特定频率的能量大小。

(16)

3 基于广义S变换故障选相及仿真验证分析

3.1 DG接入故障选相原理

由于故障分量法仍然适用于DG并入的电网，故可利用故障分量电流的广义S变换能量值来判别系统的故障类别，根据非故障相在故障后其故障分量电流始终很小，其值主要是由于电磁耦合的影响而产生的高频暂态信号，因此其S能量值远小于故障相。为了区分接地故障与相间故障，利用零序电流S能量值与三相故障电流分量S能量最大值的比值作为判据，即

(17)

式中：E0为零序电流S能量值，Ea、Eb、Ec三相故障电流分量S能量；ε为可靠系数，为了提高辨识度，可取0.001。满足式(17)则可判定为接地故障，不满足是则判定为相间故障或三相故障。由于在不同条件下，能量值的大小差异较大，为了更适合分析，取比值

(18)

其中φ=a，b，c对应A，B，C三相。对该比值进行分析，当系统发生不对称故障时，非故障相的值会很小近似为0，而发生三相短路时，由于其为三相对称短路，因此并不会出现比值为0的项，以此来判断出故障类型，达到选相目的。为了提高可靠性，判断不对称故障时将比值小于0.1的视为非故障相。具体的DG接入故障选相流程图如图1所示。

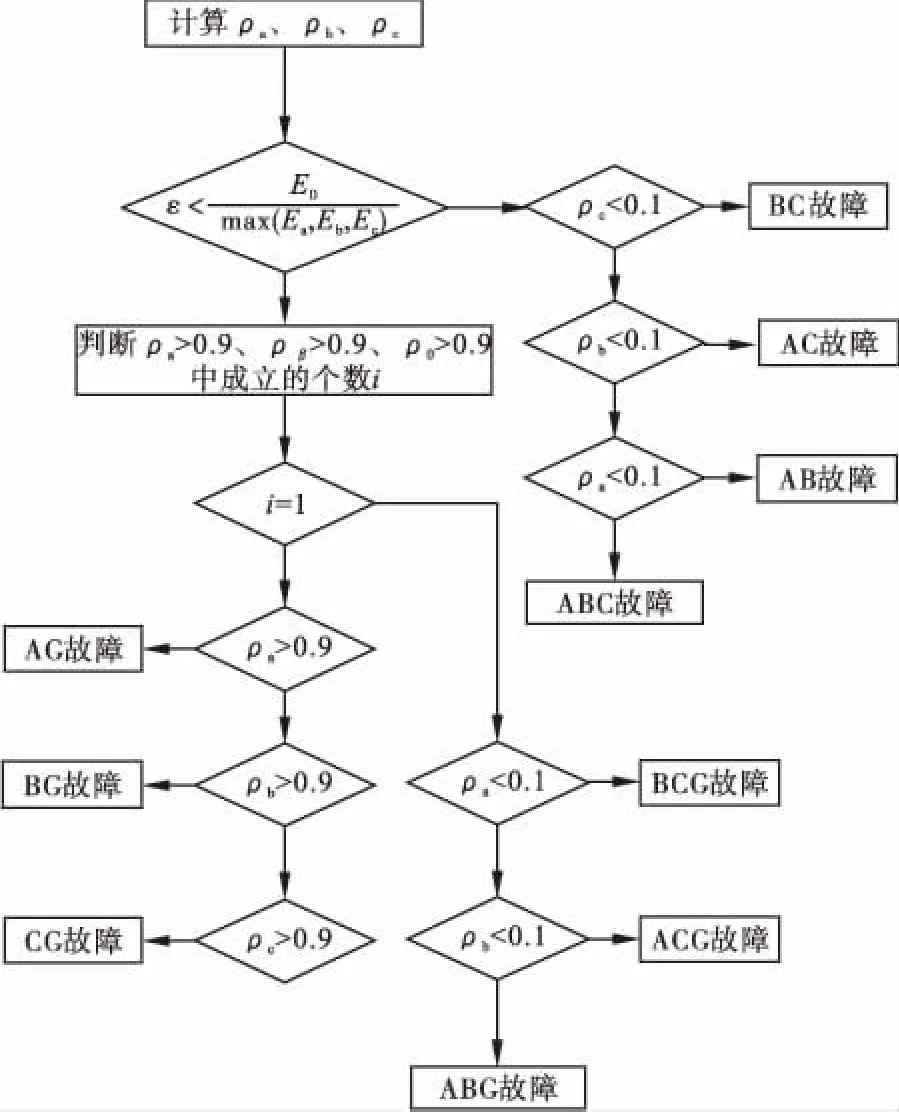
图1 故障判断及选相流程图

3.2 仿真验证

利用PSCAD/EMTDC仿真平台搭建一个含IIDG的电网模型，系统容量为S=100MVA，基准电压为10.5kV，有功功率P设置为20MW，无功功率Q设置为0，负荷采用恒阻抗型load1=20+j2.2MVA，负荷load1=25+j4MVA，Z=0.12+j0.16Ω/km，l1=l2=l3=1.5km。采样频率为20kHz，对故障前3/4周期与故障后1/4周期进行采样，采样点数为400。计算能量时提取300～320位置的时间点能量，即故障发生后的1ms内的数据，排除了广义S变换所带来的边缘效应，使结果更具可靠性。

本文通过设置不同位置、不同过渡电阻，不同类型故障等角度，验证该选相方法在不同故障条件下的适用性。由于仿真结果较多，选取具有代表性数据。

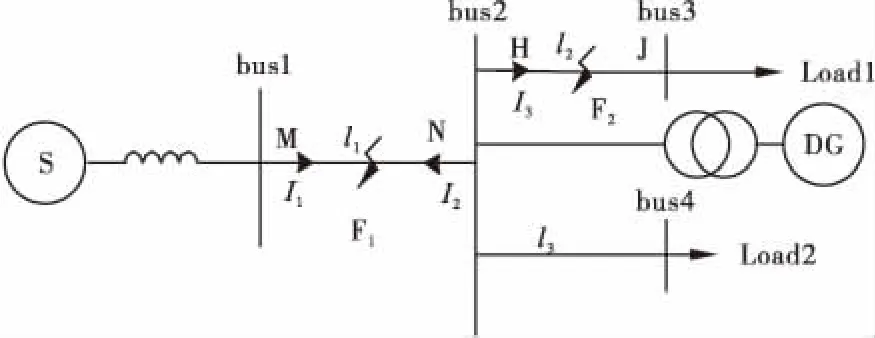
图2 含DG电网示意图

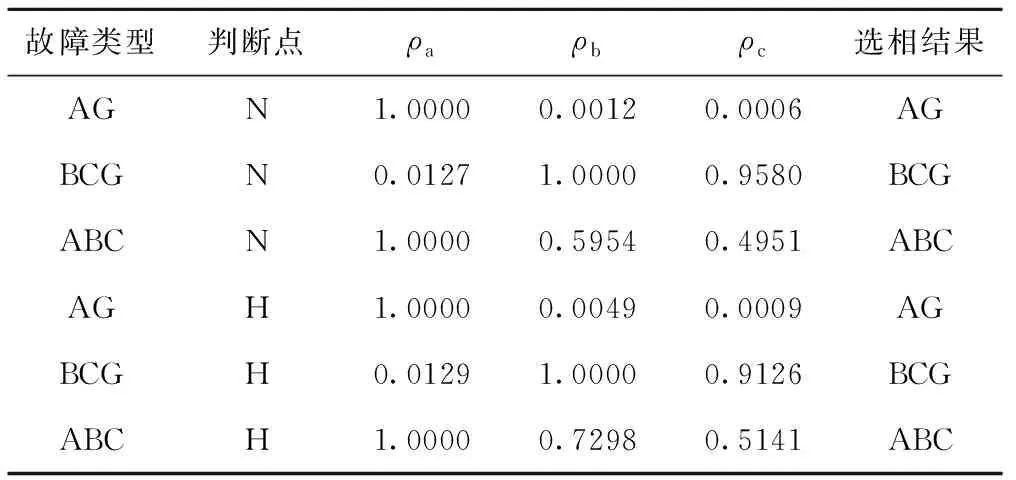
故障类型判断点ρaρbρc选相结果AGN1.00000.00120.0006AGBCGN0.01271.00000.9580BCGABCN1.00000.59540.4951ABCAGH1.00000.00490.0009AGBCGH0.01291.00000.9126BCGABCH1.00000.72980.5141ABC

表2 l2故障，过渡电阻为50Ω，故障角为0°， N、H处选相参数

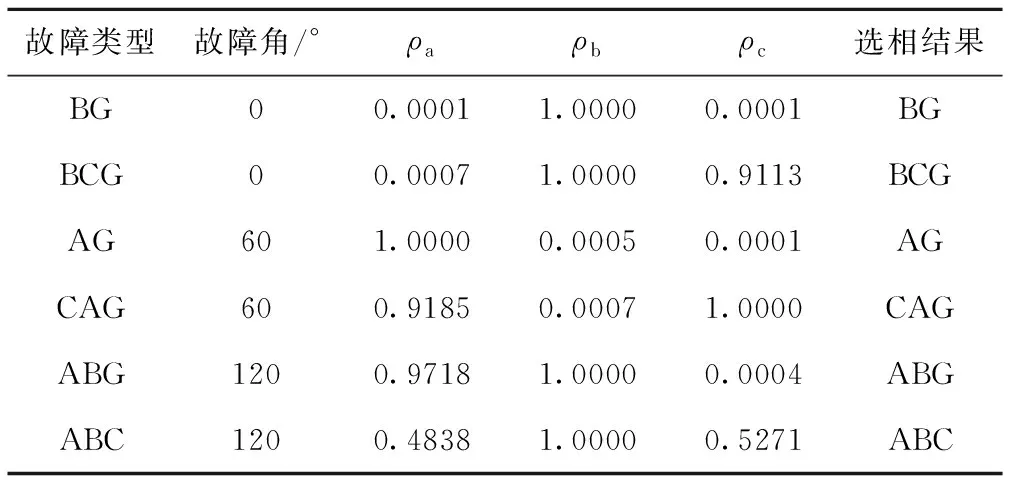
表3 l1故障，过渡电阻为0Ω，故障角为0°、 60°、120°时M处选相参数

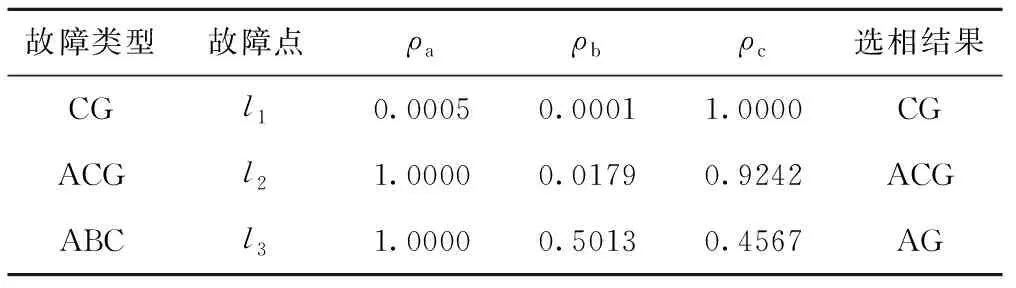
表4 l1、l2、l3故障，过渡电阻为0Ω，故障角为30°，N处选相参数

由上述的仿真结果可知：(1)故障相的电流分量能量远大于非故障相，非故障相能量可视为0，以此可区分故障相与非故障相。(2)在单相接地与两相接地短路时，存在着0模能量；相间短路与三相短路的0模能量为0，可以作为判据区分故障类型。(3)根据广义S变换能量值加权信息熵能有效的判断出含DG电网的故障类型及故障相。

4 结论

通过广义S变换能使信号特点同时反映在时域与频域中，据此特点能够精确有效提取出需要的时间段与离散频率处的广义S变换幅值，得到各离散频率的在该时段内的能量，进而进行故障判断。通过仿真结果可以看出，使用信息熵加权的广义S变换能量值的故障判断及选相方法，同样适用于DG接入并网运行的电网中，在故障发生后可以正确完成故障判断及选相的工作。