基于MCPO模型的变压器故障诊断方法

，，，

(东北电力大学电气工程学院，吉林 吉林 132012)

1 引言

电力变压器作为电力系统中的关键设备，其运行状况直接影响整个系统的安全稳定运行[1]。变压器内部结构复杂、故障类型众多，如何及时准确地辨识电力变压器的潜伏性故障，一直是输变电领域的研究热点[2]。目前，变压器油中溶解气体分析法(dissolved gas analysis，DGA)是电力变压器诊断内部故障性质的重要方法[3]。基于DGA的常用诊断方法为IEC的三比值法、改良电协研法等传统诊断方法[4]，上述方法在实际应用中存在编码不全、编码边界绝对化等缺点[5]。

近年来，国内外学者将人工神经网络(ANN)[6]、灰色理论[7]、专家系统[8]和支持向量机(SVM)[9]等人工智能算法引入到变压器故障诊断领域。其中，支持向量机因所需训练样本数据少、泛化能力强等优点广泛应用于变压器故障诊断中[9-12]。文献[10]利用PSO算法对LS-SVM诊断模型的参数进行优化，利用优化后的LS-SVM模型进行变压器故障判断。文献[11]利用SVM构建了变压器故障组合预测模型，并与多种预测方法进行比较，结果表明上述模型提高了诊断的精度。文献[12]利用多核学习向量机将模型分解为2个凸优问题进行求解，降低了计算复杂度。以上基于SVM的智能算法最终均是以故障类型作为诊断的结果，但是考虑到变压器结构复杂，故障现象与故障特征间存在着模糊性，其仍存在误诊断问题。

本文提出一种基于MCPO模型的变压器故障诊断方法，模型的输入为DGA数据和变压器故障类型，输出为发生每种类型故障的概率估计。实例分析表明，基于MCPO模型的诊断结果能够有效识别故障特征不显著的样本，为进一步开展合理的校正措施提供了一定的依据。

2 MCPO模型

2.1 支持向量机

支持向量机的本质是在训练样本数据中找出用于构造最优分类超平面的支持向量，在数学上可归结为求解一个二次优化问题[13]。

设一组样本(xi，yi)，xi为样本数据，yi为样本类别标志。最优分类超平面问题的求解可转化为求解带约束条件的优化问题：

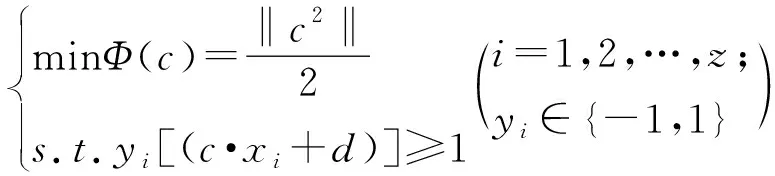
(1)

式中：z为训练样本总数;c为超平面法线;d为分类阈值。

对于线性不可分的样本，在约束条件中引入松弛变量γi来解决分类误差问题，由此可得到线性不可分时的最优分类面，其可表示为如式(2)所示的优化问题:

(2)

式中：C的作用是控制对错分样本的惩罚程度。

利用拉格朗日函数求解上述优化问题：

(3)

式中：ai为拉格朗日乘子。

对于非线性问题，SVM通过引入核函数实现某一非线性变换后的线性分类。本文采用RBF作为模型的核函数：

(4)

则SVM的分类决策函数为：

(5)

2.2 SVM概率输出

本文采用文献[14]的方法利用Sigmoid函数将f(x)映射在区间[0,1]，则概率输出表达式：

(6)

式中：A，B为Sigmoid函数的待定参数。

Sigmoid函数的参数A，B可通过最小化交叉熵误差函数获得，其求解模型可表示为：

(7)

其中：

(8)

式中：N是样本类型为yi=1的样本个数，N′是样本类型为yi=-1的样本个数。

式(8)可利用牛顿法获得最优解，即令F(a，b)的梯度矩阵等于0时的解为最优解。获得参数A，B后，则可利用Sigmoid函数将f(x)映射成概率输出形式。

对于一个二分类问题，利用式(6)可获得x属于某一类(k或l类)的概率估计gkl：

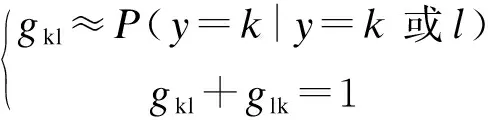
(9)

电力变压器的故障类型众多，其诊断的过程应属于多分类问题。一个q分类的问题应该综合考虑1/2q(q-1)个二分类SVM的结果，进而将其gkl综合为多分类的概率输出，则x为每一类的概率pk可表示为：

(10)

本文利用文献[15]给出的从二分类概率得到多分类概率的方法实现多分类的概率输出。考虑有：

(11)

即：

gkl/glk≈pk/pl

(12)

对上式进行变换并求和：

(13)

利用式(13)求解以下模型进而获得pk：

(14)

上述模型的求解可转化为求解一个凸二次规划问题：

(15)

当满足公式(15)时，其获得最优解。

(16)

式中：e=[1,1,…,1]T，pT=[p1,p2,…,pq]。

3 基于MCPO的变压器故障诊断方法

3.1 诊断模型输入

电力变压器正常运行时，变压器油中所含有的气体主要是氧气和氮气[3]。当变压器发生故障时，变压器油中含有一定量的故障特征气体。本文选取H2、CH4、C2H6、C2H4、C2H2这五种气体作为故障特征气体，则诊断模型的输入为(x，y)，其中x是故障特征气体含量；y为变压器故障类型，本文所考虑的故障类型见表1。

表1 变压器故障类型

考虑上述五种特征气体含量差异较大，为了减少计算误差，按式(17)对其进行归一化处理。

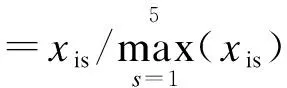
(17)

式中：xis为第i个样本第s类故障气体的含量。

3.2 诊断模型输出

MCPO模型的输出为发生每种类型故障的概率估计，记输出向量Y=(pT1，pT2，pT3，pPD，pD1，pD2)。pT1，pT2，pT3，pPD，pD1，pD2分别代表变压器的状态为T1，T2，T3，PD，D1，D2的概率。

3.3 选取模型参数

本文采用网格搜索的方法，对训练样本集进行交叉验证，并选择其中准确率最高的一组(C，σ)作为模型的参数，从而实现模型参数(C，σ)的最优选择，最优参数的计算过程如下所示。

(1)给定参数(C，σ)；

(2)将样本随机分成k个互不相交的子集，每次选择一个子集作为测试集，其他作为训练集；

(3)训练SVM，计算验证集fi；

(4)k个子集交叉验证形成Sigmoid函数的训练集(fi，yi)，训练Sigmoid函数的参数A，B；

(5)计算全部skl，得到多分类概率估计pk，若完成对所有子集的计算，则计算交叉验证的准确率。否则，返回到第二步。

3.4 诊断流程

(1)数据处理，归一化输入特征向量，形成训练、测试集样本；

(2)确定最优参数(C，σ)；

(3)利用最优参数训练SVM及Sigmoid函数的参数A、B，进而获得诊断模型；

(4)应用诊断模型对测试样本进行故障诊断。

4 算例分析

本文利用300组已确定故障类型的样本进行基于MCPO模型的故障诊断研究，训练集和测试集的分配情况见表2。

表2 样本分配表

模型参数(C，σ)分别在取值范围[2-15，2-14，…，214，215]，[2-7，2-6，…，26，27]内以指数增长方式获取。将训练样本分为5组进行交叉验证，得到的最优参数为(2-1，23)。表3列举了10组测试样本的DGA数据。表4给出了基于MCPO模型的变压器故障诊断结果。

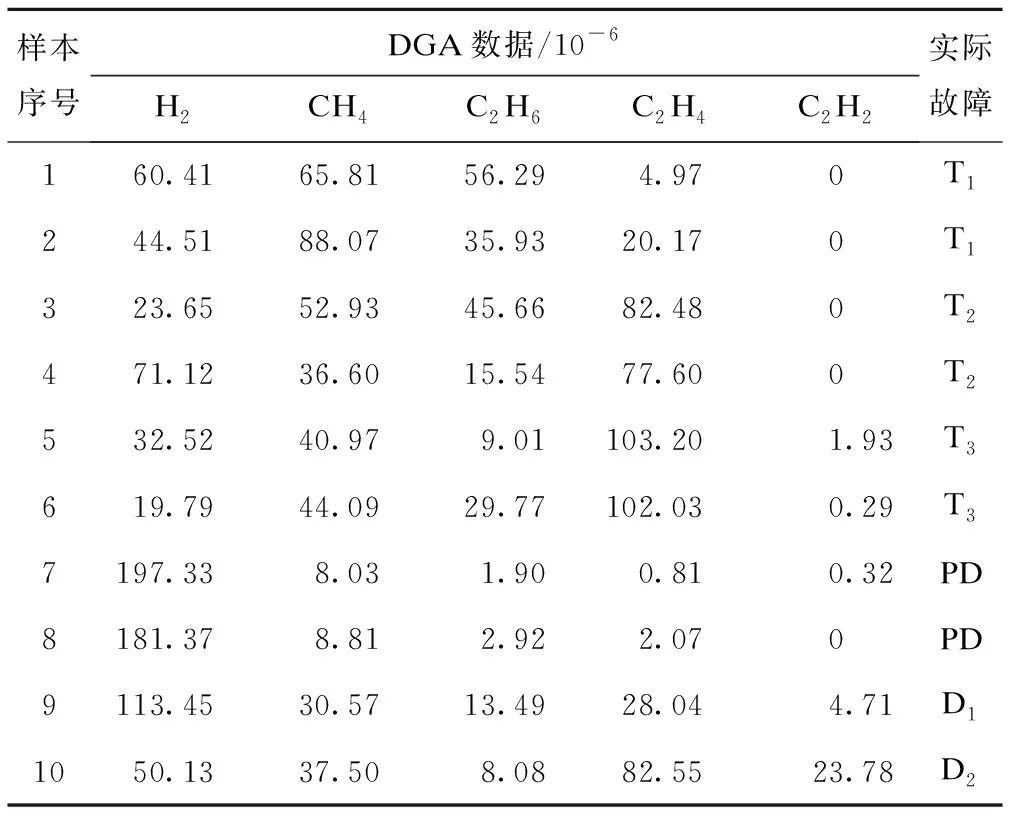
表3 部分测试集DGA数据

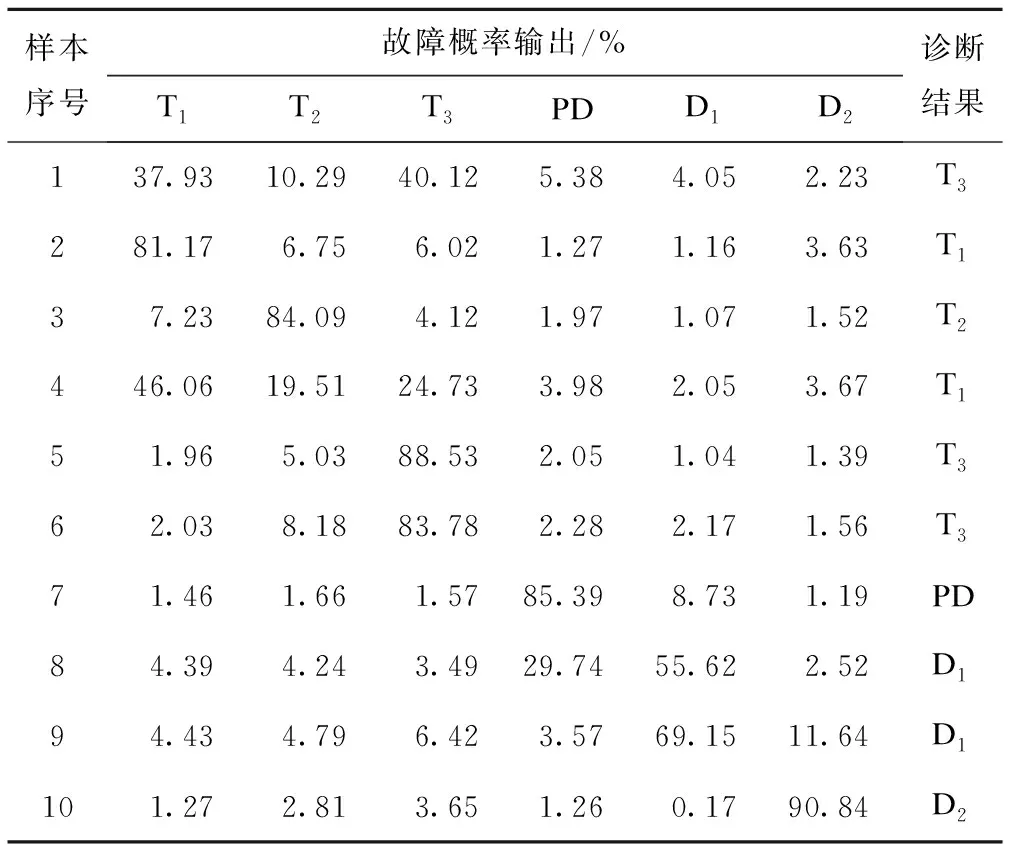
表4 MCPO模型诊断结果

由表3可知，MCPO模型的诊断结果是变压器状态为每类故障的概率。如果将概率最大作为判断故障类型的依据，基于MCPO模型的故障诊断正确率为90%。考虑到上述诊断方法在故障特征不明显的情况时存在一定的误判，本文给出以下两种故障诊断方法。

利用MCPO模型的故障诊断数据计算Pm和δ，其中，Pm=max{p1、p2、p3、p4、p5、p6}，δ为{p1、p2、p3、p4、p5、p6}的标准差。本文计算了所有测试集的Pm和δ，计算结果见图1。与表4对应的10组测试样本的计算结果见表5。

由表4可知，如果将概率最大作为判断故障类型的依据，样本1、4、8将会导致误判。由表5可知，上述三个样本的Pm分别为39.72、43.17、57.91；δ分别为0.16、0.16、0.20，Pm和δ取值相比较其他样本较小。结果表明，故障特征明显的样本，样本故障分类概率相差较大，Pm、δ取值较大；故障特征不明显的样本，样本故障分类概率较为接近，Pm、δ取值较小。由图1可知，对于故障特征不明确的样本集中分布在Pm<0.6和δ<0.25的区域中。因此，本文给出评价指标为Pm=0.6和δ=0.25，即Pm<0.6且δ<0.25的样本为故障特征不明确的样本。对于这类样本需要利用MCPO模型的诊断结果针对可能存在的故障做出相应的校正措施。

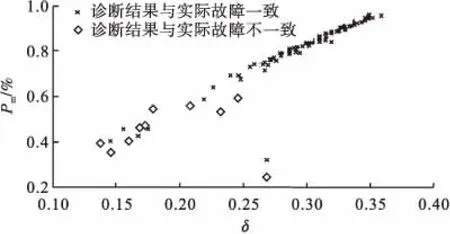
图1 Pm、δ计算结果

样本序号Pmδ140.120.16281.170.29384.090.32446.060.16588.530.32683.780.30785.390.31855.620.20969.150.241090.840.33

表6给出了采用SVM方法和MCPO方法对同样的样本进行故障诊断得到的结果。

表6 不同诊断方法的比较

由表6可知，故障特征显著的样本利用SVM方法和MCPO方法都能有效的辨别故障类型；而故障特征不显著的样本，利用SVM方法会导致误诊断。针对故障特征不明确的样本，MCPO方法可依据诊断结果参考概率较大的两三个故障类型进行相应的校正措施，进而有效弥补了传统SVM误诊断的不足。

5 结论

本文提出的基于MCPO模型的故障诊断方法能够应用于变压器故障诊断，具有较高的诊断精度，并能够提供概率信息。针对故障特征不显著的样本，基于诊断结果可参考概率较大的两三个故障类型进行相应的校正措施，进而减少了对变压器故障的误诊断。仿真分析结果验证了该方法能够有效的辨识故障特征不显著的样本，为进一步采取有效的校正措施提供一种参考。