微小水滴撞击深水液池空腔运动的数值模拟及机理研究∗

裴传康 魏炳乾

(西安理工大学,省部共建西北旱区生态水利国家重点实验室,西安 710048)

(2018年7月28日收到;2018年9月20日收到修改稿)

1 引 言

液滴下落冲击不同介质的运动过程在科技应用及自然现象中广泛存在.液滴冲击液体表面的研究在犯罪取证、开发不可浸润表面或完全可浸润表面、高精度活化或表面污染物转移等方面有诸多应用[1],液-液界面的部分聚结过程也是许多复杂物理现象的组成部分,与地球物理学与土力学等有诸多关联[2,3];对于海洋、湖泊等大面积水面,其广泛的自然掺气现象主要取决于水滴撞击所引发的气泡夹带[4];在水利工程中,高水头泄水建筑物的雾化、掺气、消能等问题也与此息息相关.因此,研究此类基本运动对于理解自然界气液流动的界面变形、改善液滴运动在工程中的应用具有重要的意义与作用.

1963年,Worthington[5]通过实验首次系统地描述了液滴和固体小球撞击液池的过程及其运动规律.随后的大量研究表明,当液滴以较低的撞击速度撞击液面时,液滴与液面发生完全聚结现象,并在液面下方生成涡环[6,7],在这种情况下,自由液面并不会出现飞溅射流,而是呈现出平坦的状态.随着液滴撞击速度的增加,自由液面开始飞溅,液面出现较大变形,产生一个空腔,并在四周形成皇冠状的射流[8],空腔塌陷后,液柱从撞击中心升起,速度较大时,由于Plateau-Rayleigh不稳定性的影响,会在液柱上方分离出一个或多个小液滴[9].一般情况下,液滴冲击液池的运动主要受重力、惯性力与表面张力的影响,因此对于弗劳德数(Fr)和韦伯数(We)十分敏感[10].

传统上对液滴运动的探索多是以高速摄像机为主要工具进行的实验研究,但由于液滴运动的复杂性,实验摄影方式较难捕捉细致的自由面边界,对诸如压力和速度等物理量的测定也十分不便.随着Hirt与Nicolas在1981年[11]提出利用流体体积法(VOF)分离两种流体构成的尖锐界面后,数值模拟在捕捉界面变形方面精度不断提升[12,13],逐渐成为了研究液滴撞击运动的有力工具.Yue等[14]对液滴撞击液面运动进行了基于相场法的数值模拟,并根据最大Oh数得到了部分融合发生的临界标准.Ray等[15]利用CLSVOF法对液滴撞击液面进行了更为具体的研究,结果表明惯性力和表面张力在很大程度上决定了液面的运动过程.Castillo-Orozco等[16]基于VOF法和表面张力模型(CSF),讨论了流体的物理化学性质和液滴冲击速度变化对二次液滴的断裂以及冠状射流的影响.戴剑锋等[17]应用CLSVOF法研究了液滴撞击倾斜表面液膜后液膜的形态演化及飞溅过程,研究表明,空气卷吸气泡数量随着冲击角的增大而减小.黄虎等[18]则建立了液滴撞击平面液膜的数学模型,采用格子Boltzmann方法探讨了相对液膜厚度和表面张力等物理参数对界面运动过程的影响.

以往对液滴撞击运动的研究多针对毫米级直径的液滴[19],驱动其空腔形成的要素主要为惯性力及重力[10],但在较小液滴尺度下,由于液滴质量及体积的减小,毛细波运动在驱动液-液界面变形及空腔形成过程中起到越发重要的作用.现有研究较少关注直径在微米层级的液滴运动及空腔形成过程以及决定微小液滴空腔运动的主要驱动力,因此,本文主要关注高速运动的微小水滴,运用基于四叉树结构自适应网格、VOF方法以及变密度不可压缩Navier-Stocks方程的开源多相流程序Gerris[20−22],研究一定物理参数范围下微小水滴撞击深水液池的液面变形及毛细波运动过程,并尝试揭示水滴撞击产生的空腔运动及形成机理.

2 计算区域及数值方法

2.1 控制方程

液滴撞击液池的运动过程可以使用带有表面张力项的变密度、不可压缩Navier-Stocks方程来描述,具体控制方程如下[20,21]:

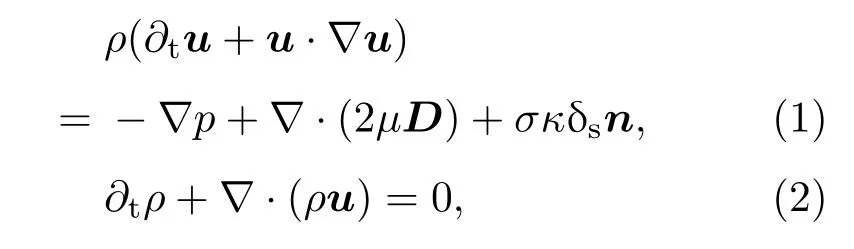
式中,ρ=ρ(x,t)为流体密度,u=(u,v,w)为流体速度,p为压力,µ=µ(x,t)是流体的动力黏度,变形张量D定义为Dij=(∂iuj+∂jui)/2,σ为表面张力系数,κ为界面曲率,狄拉克分布函数δs表示表面张力仅作用于两相界面处,n为两相界面的法向量.

Gerris采用经典的VOF方法追踪相界面,对于两相流动,引入计算网格中第一种流体的体积分数c(x,t),并定义混合流体的密度和黏度为:

式中,ρ1,ρ2,µ1,µ2分别是第一种流体和第二种流体的密度以及黏度;函数˜c由体积分数c平滑处理后得出,以便提高计算的稳定性.

密度对流方程可由等效的体积分数对流方程替换

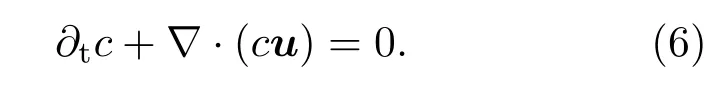
2.2 数值方法

本文数值模拟采用基于Linux的开源软件Gerris进行,该软件使用基于四叉树(二维)/八叉树(三维)的自适应空间离散方法,使用分步投影方法求解变密度不可压缩的Navier-Stocks方程,使用VOF方法跟踪相界面.高度函数和界面附近的自适应网格细化可以精确表示表面张力作用,对流项使用Godunov格式求解,并行计算采用MPI库进行.

如图1所示,水滴撞击深水液池的数值模拟在轴对称坐标系中进行,Y轴为计算区域的对称轴,D为初始水滴直径,R=D/2,正方形计算区域的长度H=20D,水滴距离液面的距离H1=0.1D,液池深度H2=12D以消除底部对液滴撞击运动的影响,水滴在重力g和撞击速度Vi的作用下撞击液池.采用雷诺数、韦伯数和弗劳德数来描述液滴撞击的运动特征,三者分别表征液体惯性力与黏滞力间的关系、液体惯性力与表面张力间的关系以及液体惯性力与重力间的关系.三个无量纲参数的表达式如(7)式所示,主要物理参数如表1所列.

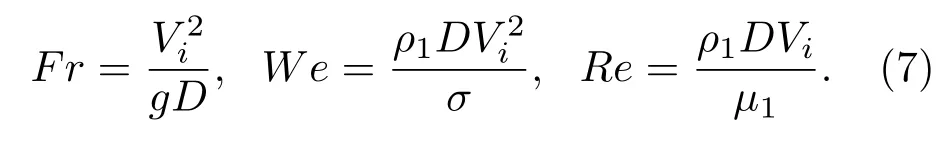
表1 主要物理参数Table 1.Main physical parameters.

图1 计算区域简图Fig.1.Schematic diagram of the computational domain.

2.3 自适应网格技术

采用数值方法对高速液滴的撞击运动进行准确的模拟极具挑战性,因为运动产生的微小界面变形、复杂的几何形状以及特征尺度的巨大差异需要足够的网格分辨率来捕捉,从而大幅地增加了计算量与计算时间.目前针对该问题的一个有效解决方法是采用自适应网格(adaptive mesh refinement,AMR)技术.根据流动特征对网格进行局部细化或粗化使得AMR技术可以将计算效率集中在最需要的区域,从而以最小的计算成本获取精确的结果.

本文采用Gerris进行数值模拟,Gerris使用有限体积法(FVM)来求解控制方程,并根据四叉树网格自适应规则和条件将计算域离散为不同等级的计算网格.水滴撞击深水液池数值模拟的关键位置在于液-液界面的交接处以及相界面附近,本文依此设计如下网格自适应规则,每一步更新一次计算网格,其中最大网格加密层数为11层,即在一个计算区域(box,Lbox=10)内的最大网格数量为211.图2为计算区域初始状态自适应网格的空间离散示意.

1)计算初始加密水滴与液池接触区域,即水滴与液池相界面处正负0.15内的网格至11层.

2)自动加密相界面附近体积分数在0—1之间、梯度变化剧烈区域的网格,最大加密到11层,最小加密到6层,以最小化界面重建产生的误差.

3)自动加密涡量变化区域的网格,根据其变化剧烈程度最大加密到11层,最小加密到4层.

4)根据U,V速度分量的变化自动加密网格,最大加密到11层.

5)限制2)—4)条规则最小加密层数的加密区间为:Y向液滴中心上方2R至水面下方4R;x向对称轴左右4R内的矩形内,以提高计算效率.

图2 计算初始状态的空间离散Fig.2.The spatial discretization of the initial simulation.

2.4 模型验证与率定

为了保证数值模拟结果的准确性,本文选择Morton的实验数据[23]对数值模型进行验证,实验使用直径为2.9 mm的液滴撞击液池,弗劳德数及韦伯数分别为Fr=220,We=248.如图3所示,照片为高速摄影机摄得的实验过程,白色线条表示相同时间节点下的数值模拟结果,t为物理时间乘以Vi/D后的无量纲时间.液滴下落后冲击液池并产生了一个空腔,腔体在t=7.9时达到最大化.空腔塌陷后毛细波向中心处传递,并坍缩形成中心射流,使其高度不断增大,在射流顶端断裂生成二次液滴.由于实验环境的复杂性,模拟条件与实验条件无法完全一致,且本文采用轴对称模型假定进行模拟,无法捕捉非对称运动,因此模拟值与实验值存在一定差异.但数值模拟在界面变形、空腔的形成与成长、毛细波在空腔底部的传播等方面与实验值取得了良好的一致性,且在空腔形成过程中给出了较实验更加详尽的毛细波运动细节,中心射流最大高度以及空腔最大深度的误差分别为1.7%,2.6%,表明数值模拟能够较好地描述液滴撞击液池的运动.

图3 数值模拟与实验结果对比Fig.3.Comparison of the numerical and experimental results.

3 计算结果与分析

3.1 基本撞击过程

水滴撞击深水液池后相界面的变化可以直观反映出水滴撞击的运动特性、水滴与池水的混掺过程以及撞击所夹带的气泡大小.因此,使用经过验证的数值方法研究直径为290µm的水滴以2.5—6.5 m/s的速度撞击深水液池的运动过程.

图4 不同工况下自由液面随时间的运动过程 (a)Fr=117.2,Re=725,We=25.2,Vi=2.5 m/s;(b)Fr=229.7,Re=1015,We=49.3,Vi=3.5 m/s;(c)Fr=379.7,Re=1305,We=81.6,Vi=4.5 m/s;(d)Fr=567.1,Re=1595,We=121.8,Vi=5.5 m/s;(e)Fr=792.1,Re=1885,We=170.2,Vi=6.5 m/sFig.4.Free surface profiles simulated at selected times:(a)Fr=117.2,Re=725,We=25.2,Vi=2.5 m/s;(b)Fr=229.7,Re=1015,We=49.3,Vi=3.5 m/s;(c)Fr=379.7,Re=1305,We=81.6,Vi=4.5 m/s;(d)Fr=567.1,Re=1595,We=121.8,Vi=5.5 m/s;(e)Fr=792.1,Re=1885,We=170.2,Vi=6.5 m/s.

水滴以五种不同撞击速度进入水池后自由表面的模拟轮廓以及水滴分布如图4所示.蓝色为气相,红色为水池部分液相,天蓝色为水滴部分液相,从工况(a)—(e),水滴的撞击速度不断增大.在图4(a)中,Fr=117.2,We=25.2,Re=725,水滴以较低速度撞击深水液池,发生完全聚结现象,并在水池中形成底部夹带一个气泡的空腔,水滴入水后基本附着在自由液面之下.随着时间增加,空腔开始向内坍缩,同时毛细波向空腔底部传递,使得水滴部分的水体向中心聚合并产生两个对称的涡,最终在空腔塌陷后对池水产生穿刺效应,池水在惯性力的作用下逐渐平复.在图4(b)—(d)中,撞击产生的空腔随着水滴撞击时动能的增加越来越大,空腔底部夹带的气泡不断变小,随着撞击速度的增大,在空腔塌陷后,一个短而粗的射流在撞击中心产生,且射流最大高度不断增加.由于毛细波的传递速度加快,水滴入水后附着自由液面的面积也逐渐变大,产生的涡距离撞击中心越来越远.在图4(e)中,Fr=792.1,Re=1885,We=170.2,水滴撞击后首先产生一个U形空腔,最大深度再次增加,随后由于毛细波的快速传播推动空腔底部部分侧壁收缩闭合,截留形成一个较大的气泡,并在闭合处产生极细的射流,射流由于竖向剪应力较大,引起Plateau-Rayleigh不稳定性,在尖端断裂生成多个二次滴,自由液面变化更为剧烈.

上述水滴撞击水池的过程可以归纳为三个基本阶段,第一阶段为空腔的形成与膨胀;第二阶段为毛细波传播导致的空腔收缩;第三阶段为空腔的回复.液滴撞击深水液池时的运动分为完全聚结与部分聚结现象[24],在水滴与深水液池完全聚结时,水滴入水时由于水滴底部发生凹陷变形产生的气泡夹带随着撞击速度的增加而减小,而在部分聚结发生时气泡的夹带与截留行为则更为复杂.

3.2 空腔运动的基本特性

为了深入探究微米级水滴撞击深水液池后空腔运动的基本特性,对本文五个模拟工况进行定量研究.描述空腔几何特征的基本参数如图5所示,以初始静水状态下深水液池的液面高度为基准线,hw为基准线至波浪顶端的波浪隆起高度,h为基准线至空腔最低点的空腔深度,r为空腔基准线上轴对称点处至空腔侧壁的空腔宽度.下文涉及的所有长度单位均为实际长度除以初始水滴直径D后的无量纲长度,时间t为实际时间乘以Vi/D后的无量纲时间.

图6为不同工况下空腔深度h随时间的变化过程.由图6可以看出,液滴撞击深水液池后,由于动能、空腔侧壁隆起部分重力势能以及表面张力能的驱动,空腔深度先以较快速度增长,其后增势逐渐放缓,在到达最大空腔深度后快速回弹,至接近原自由液面后回弹速度逐渐放缓,近乎趋于直线.弗劳德数的增加对空腔深度变化影响显著,在工况(a)中,弗劳德数仅为117.2,空腔能量耗散时程较短,回复较为迅速,随着弗劳德数的增大,撞击动能增大,回复时程也逐渐增加.值得注意的是,在工况(e)中,由于空腔形状由U形转变为近似梯形,空腔在t=1.5—2.6时先缓慢上升,随后毛细波向空腔底部传递,促使其底部变为圆柱形,且深度继续增加,最后空腔底部侧壁坍塌形成射流,因此在t=2.6后空腔回复速度较其他工况更为迅速.将数值结果运用最小二乘法拟合,得到的拟合曲线表达式如(8)式所示,该式能够在忽略毛细波运动的前提下,在空腔深度为h=D至达到最大深度的范围内较好地描述了空腔深度随时间的成长关系,Liow等[8]与Ray等[24]对液滴撞击运动中时间与空腔深度的关系进行了建模,得出与本文相似的结论:

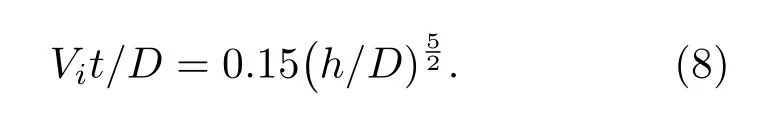
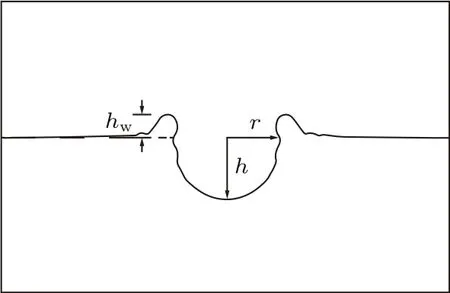
图5 空腔的几何特征示意Fig.5.Geometric characteristics of the cavity.

图6 不同工况下空腔深度随时间的变化Fig.6.Cavity depth with time under different conditions.

图7及图8分别为不同工况下波浪隆起高度hw和空腔宽度r随时间的变化过程.由图7易得,水滴撞击水池后波浪高度的变化过程也经历了从快速增长到逐渐回落,最终在惯性力的作用下自主运动,趋于稳定的过程.随着弗劳德数的增大,更大的垂向速度在创造更深空腔的同时激发了更高的最大波浪隆起高度.从图8可以看出,空腔宽度的增长与波浪的运动息息相关,在撞击产生的动能与波浪自身重力势能基本耗散后,空腔运动主要由毛细波及其干扰驱动,最后在惯性下线性增长.毛细波现象在图8工况(e)的t=0.8时非常显著,其周期在图6的t=1.5—2.5中也有体现.

图7 不同工况下波浪隆起高度随时间的变化Fig.7.Wave height with time under different conditions.

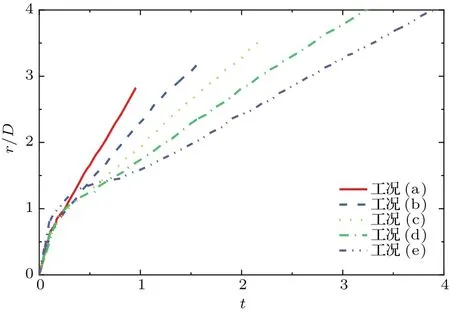
图8 不同工况下空腔宽度随时间的变化Fig.8.Cavity width with time under different conditions.

3.3 空腔形成以及毛细波传播机理

选取水滴完全聚结的工况(d)与水滴部分聚结的工况(e)对空腔形成以及毛细波传播的机理进行深入研究.图9为不同时间节点下工况(d)及工况(e)水滴撞击深水液池空腔运动的等值线图,其中左侧为涡量场等值线图,右侧为压力场等值线图,黑色线条表示相界面.由图9(a)可得,水滴撞击液池后,空腔形状由U形向V形转变,最终腔底首先上升,形成没有气泡截留的射流.

Berberovic等[25]的研究表明,毛细波的传播路径与低压区的形成息息相关.在图9(a)压力场等值线图中可以看出,低压区首先在空腔侧壁与底部的交界处产生,随后向空腔底部传播,并形成一个相对尖锐的点,在空腔底部上升后,毛细波开始向下方传递,并逐渐趋于平缓.

在发生部分聚结现象的图9(b)中,低压区首先在波浪底部与侧壁上交界处产生,并已经在相界面上形成了一个尖锐的折点,此时空腔形状为半球形,随后毛细波向空腔底部传播,在底部中心空腔转变为圆柱状,低压区附着在圆柱下方与底面交点,毛细波在空腔坍塌前并没有到达空腔底部中心,而后空腔侧壁坍塌形成气泡截留,并在中心产生了快速射流液柱.

涡量定义为流体速度矢量的旋度,描述液体流动的剪切运动.在工况(d)中,如图9(a)涡量场所示,流体涡量一直跟随毛细波位置,当空腔坍塌产生慢速射流时,涡量在靠近液面区域以及空腔底部靠近对称轴的区域各产生一个较大的涡环,而在工况(e)中,涡环的生成被抑制,流体仅在t=1.906时表现出一个靠近空腔底部的小涡环,而后涡环迅速消失.由涡量场与压力场对比可得,涡量较大的区域并不总是处于低压区内,撞击运动初始自由液面的压力差可能是涡量产生的诱因,但其后低压区的运动与涡量之间并无较强的相关性.

4 结 论

本文采用基于自适应网格和VOF方法的开源程序Gerris对微小水滴撞击深水液池后的流动过程以及空腔生长进行了数值模拟,研究了不同Fr数对撞击后空腔毛细波运动以及气泡截留的影响,主要得到以下结论.

1)在恰当的自适应条件下,Gerris程序能够在节约计算资源的同时较为准确地预测水滴撞击深水液池的运动,数值模拟所得的界面变形、空腔成长、毛细波的传播以及中心射流过程与实验结果符合良好.

图9 不同时间节点下水滴撞击深水液池空腔运动的涡量场和压力场等值线图 (a)Fr=567.1,Re=1595,We=121.8;(b)Fr=792.1,Re=1885,We=170.2Fig.9.Vorticity and pressure contours at selected time:(a)Fr=567.1,Re=1595,We=121.8;(b)Fr=792.1,Re=1885,We=170.2.

2)液滴下落撞击深水液池后,液面扩张形成一个空腔,其后随着毛细波运动逐渐回缩.液滴完全聚合时,空腔形状往往由U形向V形转变;在液滴部分聚合生成细长中心射流并产生气泡截留时,空腔初始形状则近似一个半球形,其后在底部变形为圆柱形.

3)液滴撞击深水液池后,空腔深度先以较快速度增长,在到达最大空腔深度后快速回弹,至接近原自由液面后速度逐渐放缓.在忽略毛细波作用、空腔深度为h=D至h=hmax范围内的前提下,空腔深度随时间的成长关系可由(Vit)/D=0.15(h/D)5/2来描述,但最终空腔底部的形成是由毛细波运动决定的;空腔宽度的增长主要由毛细波运动及其干扰驱动,最后在惯性力作用下线性增长.

4)毛细波运动可由压力场中低压区的位置示踪,在撞击速度较低,液滴完全聚结时(Fr=567.1,Re=1595,We=121.8),低压区首先在空腔侧壁与底部交界处产生,随后向空腔底部传播,在靠近液面以及空腔底部靠近中心区域各产生一个较大的涡环;在发生部分聚结现象,产生细长射流时(Fr=792.1,Re=1885,We=170.2),涡环的生成被抑制,低压区首先在波浪底部与侧壁上交界处产生,空腔底部变为圆柱状后,毛细波在空腔坍塌前并没有到达空腔底部中心,导致空腔侧壁首先坍塌形成气泡截留.

感谢西安理工大学水力学研究所的李林博、杨泓、薛博升和杨琰青在论文完成过程中的帮助与讨论.