平面向量奔驰定理与三角形四心的应用
2018-12-18 05:41:34
新教育时代电子杂志(学生版) 2018年18期
(四川省德阳中学校 四川德阳 618000)
奔驰定理:
已知O 是 ∆ABC内的一点, ∆BOC , ∆AOC,∆AOB 的面积分别为

图1

图2
如图2延长OA与BC边相交于点D则


有此定理可得三角形四心向量式

三角形“四心”的相关向量问题与“重心”有关的向量问题
A.重点 B.外心 C.内心 D.垂心
2.知△ABC 中,G是重心,三内角A,B,C的对边分别为a,b,c,
解:由奔驰定理可知:
5 6a = 4 0b =3 5c, 不妨设a=5k ,b =7k,c =8k,由余弦定理可得:B=6 0o
●与“垂心”有关的向量问题
3.已知O是平面上一定点,A,BC是平面上不共线的三个点,动点P 满足:

则动点P 的轨迹一定通过△ABC的( )
A.重点 B.外心 C.内心 D.垂心

●与“内心”有关的向量问题
4.已知O 是平面上一定点,A,BC是平面上不共线的三个点,动点P 满足
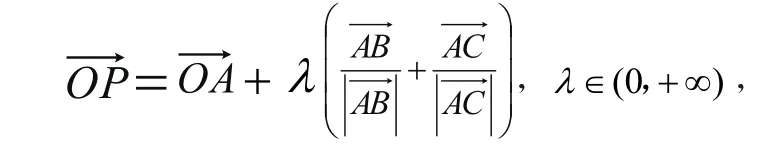
则动点P 的轨迹一定通过△ABC的( ).
A.重点 B.外心 C.内心 D.垂心
●与“外心”有关的向量问题
5.已知O是平面上的一定点,A,B,C是平面上不共线的三个点,动点P满足:

则动点P的轨迹一定通过△ABC的( )。
A.重点 B.外心 C.内心 D.垂心

●四心的相互关系
1.设△ABC 的外心为O,则点H为△ABC 的垂心的充要条件是
2.设△ABC 的外心为O,则点G为△ABC的重心的充要条件是
3.设△ABC的外心、重心、垂心分别为O、G、H,则O、G、H三点共线(O、G、H三点连线称为欧拉线),
猜你喜欢
中学生数理化·高一版(2023年2期)2023-03-23 02:17:06
中学生数理化·高一版(2023年2期)2023-03-23 02:17:02
新高考·高一数学(2022年3期)2022-04-28 07:02:46
学校教育研究(2022年7期)2022-04-24 16:35:10
中学生数理化·高一版(2022年2期)2022-04-05 13:48:54
中等数学(2021年6期)2021-08-14 02:35:48
中等数学(2021年4期)2021-08-14 02:34:40
数学学习与研究(2017年13期)2017-07-21 13:12:12
新闻前哨(2016年11期)2016-12-07 11:41:34
新教育时代·教师版(2016年27期)2016-12-06 18:19:56

