巧解选填之神出鬼没的特例法
(黑龙江省密山市第一中学 黑龙江密山 158100)
特例法具有简化运算和推理的功效,此法是用特殊值(或特殊函数、特殊位置、特殊数列等)代替题设普遍条件,得出特殊结论,此种考虑不失一般性,然后对各个选项进行检验,从而做出正确的选择。
选择题和填空题是高考中的重要题型,在新课标二卷中,选择题题12道,60分,填空题4道,20分,选填共80分,占全卷分数比重的53.3%。如何才能在考试中快速且准确的完成选择题和填空题,并未后续的大题赢得时间的?本文着重围绕解决选填的常用方法中的一种展开----特例法。
特殊值法,解题中由于选择题的答案是唯一确定的,所以可以通过设题中某个未知量为特殊值,一般选择的是较小、较规整的数,从而通过简单的运算,得出最终答案的一种方法。

综上可知:m<0。本题考查函数的奇偶性、单调性及应用,函数与不等式的关系。
解法二:(特殊值法)当m=0时,得f ( 0 ) + f(1) = 2 > 0,显然成立。可排除A、B;
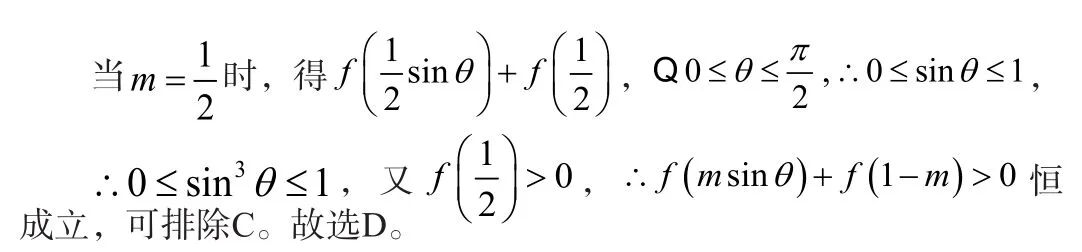
特殊函数法,解题中对于大部分的抽象函数问题,通过设题中某些已知条件,选取特殊的函数解析式,首选常函数,然后是一次函数,二次函数,三次函数,指数函数等,从而通过简单的运算,得出最终答案的一种方法。

解法二:(特殊函数法)本题为抽象函数问题,符合条件的函数有很多,本题可选取函数f( x)=2,则不等式可转换为ex⋅2 > ex+1,即ex>1,得x>0。故选A。
例4.已知函数f(x)(x ∈ R),满足f ( − x ) = 2−f(x ),

[答案]B
解法一:(直接法)略
解法二:(特殊函数法)本题可取符合条件的函数f(x ) = x+1联立方程组,可解得交点坐标为(− 1 ,0 ) 、(1 , 2),由题意知m 为交点x个 数,
故选B。
特殊数列法,一般情况下,确定一个等差或者等比数列需要两个条件。解题时题干中对数列的控制条件少,不足以限定数列的通项公式时可选择符合条件的特殊数列解题,从而通过简单的运算,得出最终答案的一种方法。
[答案]15
解法一:(直接法)略
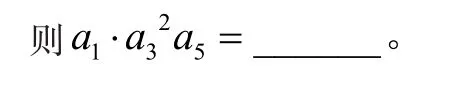
解法一:(直接法)略
解法二:(特殊数列法)本题可取符合条件的数列--常数列,甚至根本不需要知道该常数列具体是多少,因为已知条件是两项相乘的所求是四项相乘,可快速得到答案
特殊图形法,在一些考题中常常给出的是一些“模糊”的条件,比如在三角形中,在平行四边形中,并没有给出具体的长度、角度等可以限定图形形状的条件,这时可以选择特殊图形进行解题。选择的特殊图形往往是等腰直角三角形、等边三角形、矩形、正方形等,从而通过简单的运算,得出最终答案的一种方法。

解法一:(直接法)略
解法二:(特殊图形法)从题意来看,本题与三角形的形状无关,所以可选择等腰直角三角形,然后建立坐标系来解决。因为有两个向量都是以A为起点,所以以A为坐标原点,本题可设腰长为3。


例8.如图所示,已知∆AOB,点C是点B关于点A的对称点,CD和OA交于的值为_______。
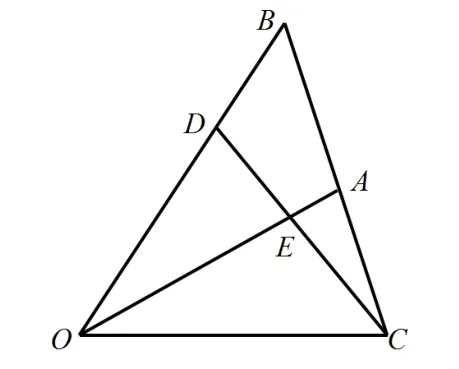

解法一:(直接法)略
解法二:(特殊图形法)本题虽然给定了图像,但仍然可采用的是图形来解决,重新

常用的特例法还有特殊角、特殊位置、特殊方程、特殊点等,本文不再举例叙述。在解决问题时,以上方法要注意灵活运用,很多情况下都是需要穿插一些其他方法综合运用,不可拘泥于一法。另外,本文选用的有选择题也有填空题,意在说明很多的方法也同样适用于填空题。总之,要力求“快”、“准”、“稳”的解决选择和填空题,小题就要小作,不能小题大做。

