车辆动态目标位置跟踪的自适应预测控制研究

莫舒玥

（广西交通职业技术学院 汽车工程系，广西 南宁 530022）

1 引言

随着公路交通的智能化，车辆智能控制技术越来越重要，其中智能车辆自主导航技术受到广泛关注[1-2]。横向控制是车辆自主导航的关键技术，其表示车辆在不同的车速、荷载、路况以及风阻等条件下自动跟踪行车路线，并保证一定的舒适性和平稳性，即车辆的转向控制。

车辆的数学模型包括动力学模型和运动学模型两种建模方式。动力学模型的构建受车载、路况、车体运动状态、环境变化等因素影响，且部分影响因素难以测量和确定，而运动学模型则从车辆运动学状态角度出发，只需要通过位置、速度或加速度等信息即可描述车辆与行车路线之间的关系，且这些描述变量都具有实时可测量性，可避免动力学模型的缺陷[3-7]，因此采用运动学模型来对被控车辆进行建模。

随着工业自动化的快速发展，控制过程变得更加复杂化，实际控制要求也变得更加严格，基于模型的控制方法依赖被控对象的精确数学模型描述，才能获得较佳的控制效果，从而导致传统模型控制方法在复杂的工业控制领域上，无法满足实际生产的控制需求。基于数据驱动的控制方法以不依赖精确数学模型的特点而逐渐受到广泛关注。其中，无模型自适应控制方法应用较广，主要是因为其控制过程仅需要被控对象的I/O数据，不需要系统的任何其他信息，即可实现控制系统的设计，且实现简单，计算负担小，正受到越来越多学者的青睐。此外，将预测控制方法与无模型自适应控制方法相结合，不仅融合了两种控制方法的优越特性，还能够进一步提高无模式自适应控制方法的泛化能力和控制效果，因此，将无模型自适应预测控制方法应用于车辆智能控制技术的研究中更具有优越性和重要意义[8-10]。

以车辆运动过程为研究对象，通过构建车辆动态目标位置的运动学模型，在无模型自适应控制方法的基础上，结合预测控制方法，研究车辆在弯道保持过程中跟踪动态目标位置的实现问题。

2 车辆动态目标位置跟踪

2.1 运动学模型

车辆的动态目标位置是指被控车辆在运动过程中，随着车辆运动位置的变化而改变的预期到达位置与状态。它可由向量T=［xt，yt，θt］来表示，xt和 yt分别表示动态目标位置在 t时刻的横向和纵向位置，θt为动态目标位置的车头方向与X坐标轴正方向的夹角，θt为车头转角，θ为动态目标位置方向角。

四轮车辆的前轮转向运动学模型可由式（1）的形式表达：

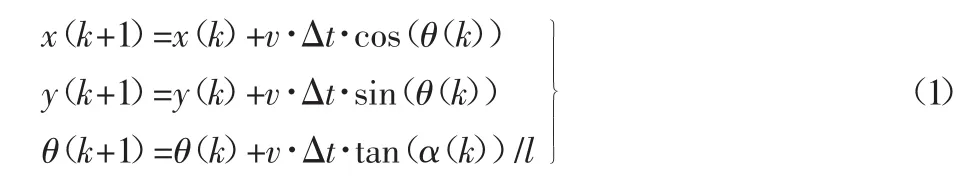
式中：v—车辆纵向轴方向的速度；Δt—采样时间间隔；θ—车辆纵向轴方向与x轴方向的夹角；α—车辆前轮参考本身纵向轴方向的转向角度；l—车辆轴距；k—仿真步数。四轮车辆的运动学模型，如图1所示。

图1 车辆运动学模型Fig.1 Kinematic Model of Vehicle

2.2 动态坐标

动态目标位置作为模拟驾驶员根据当前周围环境状况决策下一时刻的要到达的安全目标位置，通常目标位置是多个存在的，这种多目标决策过程是非常复杂的。为简化问题，只考虑单个目标的情形。

针对动态目标位置的跟踪控制，需建立车辆的绝对位置和动态位置之间的坐标变换关系，即将车辆的绝对坐标位置转化为以车辆后轴中心为原点，以其车头方向为x轴正向的动态坐标位置，如图1所示。图中，受控车辆与目标位置在全局坐标系下的坐标分别为（X0，Y0）和（X1，Y1）。

由几何关系可知，其动态坐标值的转换关系可由式（2）表示：

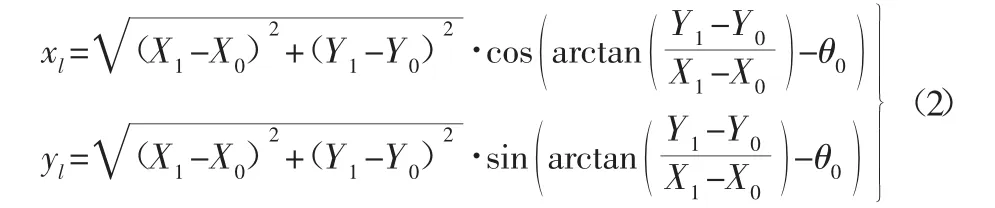
在动态坐标系中，动态目标位置方向角与受控车辆车头方向角之差 θ1可表示为

式中：θ0—绝对坐标系中车辆的实时车头方向与x轴方向的夹角；θ—动态坐标系中动态目标位置的方向与x轴方向的夹角。

3 无模型自适应预测控制器设计

3.1 无模型自适应控制算法

基于紧格式动态线性化的传统无模型自适应控制算法，其线性化模型为：

式中：Δu（k）＝u（k）-u（k-1），φc（k）—伪偏导数，为一个有界的数。

3.1.1 估计如下偏导数

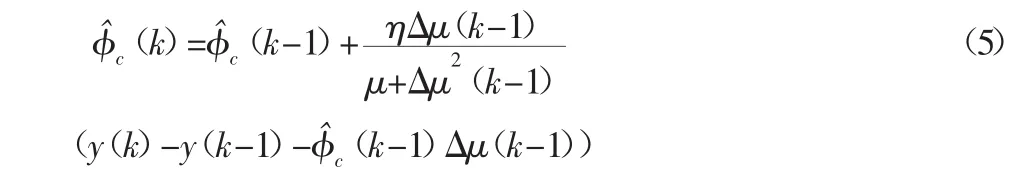
式中：μ＞0—伪偏导数权重因子；φˆc（k-1）—伪偏导数上一时刻估计值；η∈（0，1］—伪偏导数步长因子。

3.1.2 计算控制输入

式中：y*（k+1）—期望输出信号；λ＞0—u（k）的权重因子；ρ∈（0，1］—输入步长因子。

3.2 无模型自适应预测控制器设计

将预测控制与无模型自适应控制相结合的控制方法进一步改善传统无模型自适应控制方法对精确模型的依赖。在传统无模型自适应控制的基础上引入预测控制理论，通过两者结合，既可以充分发挥传统无模型自适应控制方法的优点，又能借助预测控制的优点弥补其不足，从而提高控制模型的效率、精度和可行性。基于无模型自适应控制和预测控制的控制器设计过程以下步骤所示：

3.2.1 控制算法计算过程

利用式（4）的线性化模型，其N步向前预测方程为：

式中：Nu—控制时域常数，则式（7）表示为：

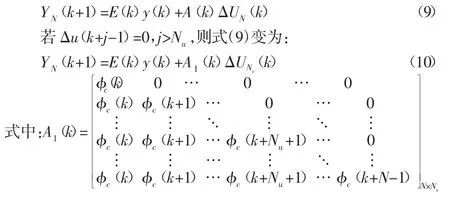
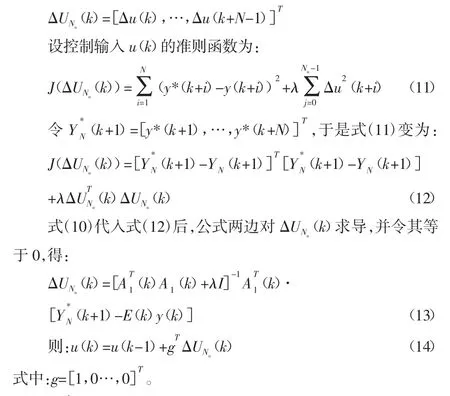
表2 PID控制器参数Tab.2 Parameters of PID Controller

3.2.2 参数估计与预报

控制算法计算过程完成后，下一步需要对A1（k）中的伪偏倒参数进行估计与预报。选择多层递阶预报方法，其计算公式为：

式中：j=1，2，…，Nu-1，θi，i=1，2，…，np—系数，通常取 np=2～7，θi的计算公式为：

根据以上计算过程可知，基于自适应预测控制方法的车辆动态目标位置跟踪系统控制器设计过程为：

Step4：计算式（13）和式（14）。

式中：ε、M—正的常数；Aˆ1（k）、φˆc（k+j）—A1（k）、φc（k+j）的估计值。

4 仿真结果对比分析

设计的车辆动态目标位置跟踪仿真工况为：车辆首先沿x轴方向直线行驶50m，再进入转弯半径为200m的左弯道上行驶90°，最后沿y轴方向直线行驶50m。车辆行驶速度为10m/s，采样时间间隔为0.1s，车辆的轴距设为1.5m。动态目标位置坐标值在仿真的每一步中根据受控车所在位置结合道路线形选取道路中心线的坐标值进行更新，动态目标位置方向则取道路中心线该点处与车辆行驶方向一致的切线方向。

为了进一步验证所提方法的有效性和优越性，结合传统PID控制方法进行对比论证。通过对比两种方法所构建的模型的仿真分析结果，证明基于无模型自适应控制方法和预测控制方法的控制器设计能够改善控制器的性能和效率。基于MATLAB分别对传统PID模型和无模型自适应预测控制模型进行仿真建模。采用MFAPC控制方法对车辆动态目标位置跟踪系统进行控制时所整定的控制器参数，如表1所示。采用PID控制方法对车辆动态目标位置跟踪系统进行控制时所整定的控制器参数，如表2所示。

表1 MFAPC控制器参数Tab.1 Parameters of MFAPC Controller

图2 MFAPC控制跟踪目标轨迹性能Fig.2 Target Tracking Performance of MFAPC Controller

图3 PID控制跟踪目标轨迹性能Fig.3 Target Tracking Performance of PID Controller

图4 MFAPC控制跟踪目标方向性能Fig.4 Target Orientation Performance of MFAPC Controller

对车辆动态目标位置跟踪系统进行控制过程中，MFAPC控制器跟踪动态目标位置的跟踪性能，如图2所示。PID控制器跟踪动态目标位置的跟踪性能，如图3所示。MFAPC控制器跟踪动态目标方向的跟踪性能，如图4所示。PID控制器跟踪动态目标方向的跟踪性能，如图5所示。MFAPC控制器控制车辆运动过程中X轴方向的偏差量，如图6所示。PID控制器沿X轴方向的偏差量，如图7所示。

图5 PID控制跟踪目标方向性能Fig.5 Target Orientation Performance of PID Controller

图6 MFAPC控制车辆X轴向偏移量Fig.6 X-Axis Direction Bias of MFAPC Controller

图7 PID控制车辆X轴向偏移量Fig.7 X-Axis Direction Bias of PID Controller

图8 MFAPC控制车辆Y轴向偏移量Fig.8 Y-Axis Direction Bias of MFAPC Controller

通过模型构建及仿真分析结果，可以得知：从图2和图3的结果可知，分别采用MFAPC和PID控制方法对车辆动态目标位置跟踪系统进行仿真，两种方法在车辆动态目标位置跟踪控制过程中都可以体现很好的控制效果，表明MFAPC方法具备PID控制的相关优势和控制效果，如图6～图9所示。MFAPC控制方法虽然在X轴和Y轴方向产生的绝对最大偏移量相比PID控制方法要大一些，但两者相差程度最大不超过0.2m，而MFAPC在整个控制过程中产生的误差波动性却比PID明显要小很多。图4和图5则说明，MFAPC控制方法在车辆从直线轨迹进入弯道轨迹，再由弯道轨道进入直线轨迹的过程中，都能够很平稳地跟踪目标轨迹，而PID方法在道路转变过程中存在波动现象。

图9 PID控制车辆Y轴向偏移量Fig.9 Y-Axis Direction Bias of PID Controller

5 结论

针对基于模型的控制方法难以解决车辆弯道保持系统中的动态目标位置跟踪问题，通过构建车辆动态目标位置的运动学模型，基于MFAPC方法实现了车辆动态目标位置跟踪系统的控制器设计，并应用MFAPC和PID方法对车辆动态目标位置跟踪系统进行了仿真结果对比分析，仿真结果表明，MFAPC控制方法相比传统PID控制方法，在车辆动态目标位置跟踪应用中具有更高的控制精度和平稳性，从而体现所提方法的有效性和优越性，为车辆的动态目标位置跟踪技术研究提供新方法和新思路。