Logistic和Generalized-Arc-Tangent产量递减方程理论推导
蔡喜东,高文君,宋红霞
(中国石油 吐哈油田分公司 勘探开发研究院,新疆 哈密 839009)
文献[1]和文献[2]分别建立Logistic产量递减方程和Generalized-Arc-Tangent产量递减方程时,均采用拟相渗关系式,这与文献[3]中Arps产量递减方程建立过程中采用拟相渗关系式而引起的不足和缺陷属同一类问题[4]。文献[5]就此类问题,对Arps产量递减方程的渗流理论进行完善,因此,为了使Logistic产量递减方程和Generalized-Arc-Tangent产量递减方程的渗流理论基础也更加完善,本次沿用文献[5]的研究思路,对Logistic产量递减方程和Generalized-Arc-Tangent产量递减方程的渗流理论进行了推导与完善。
1 基础理论方程
注水保持地层压力的情况下,油藏物质平衡微分方程可表示为[6]

油井开井数保持不变时,油田总产量由下式计算[7]:
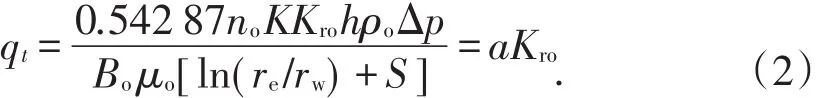
将(1)式代入(2)式,得

油井见水以后,平均含水饱和度Sˉw由Welge方程得到[8]:
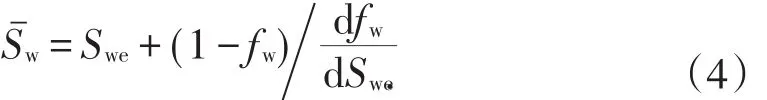
在不考虑毛细管力、重力的影响时,由Darcy式可得到分流量方程[9]:
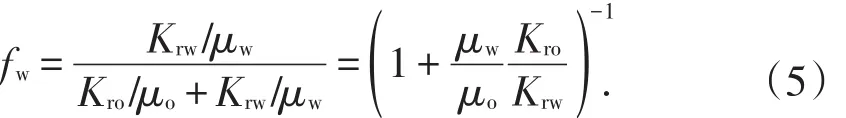
2 Logistic和Generalized-Arc-Tangent产量递减方程的理论推导
艾富罗斯实验结果表明,平均含水饱和度与出口端含水饱和度一般符合线性关系[8]:
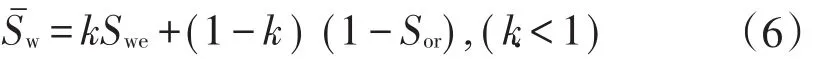
对上式两边微分,得

2.1 Logistic产量递减方程
2007年,文献[10]曾提出油相相对渗透率较符合下式:
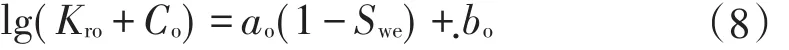
令 Ko(Swi)=exp[bolg(e)+(1-Swi)aolg(e)]-Co,m=(1-Swi-Sor)aolg(e),则(8)式可写成归一化含水饱和度关系式:

式中 Swd=(Swe-Swi)/(1-Swi-Sor).
将(7)式和(9)式代入(3)式,取初始条件递减时间t=0时,Swe=Swi,定积分,得
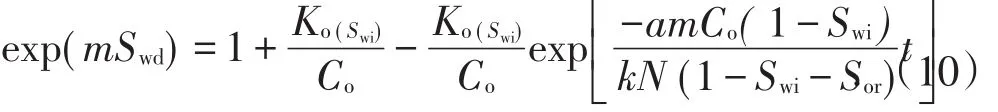
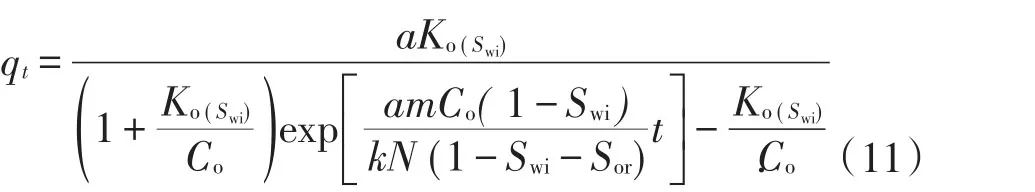
将(10)式代入(2)式,整理,得
令t=0,得

那么,(11)式可改写为
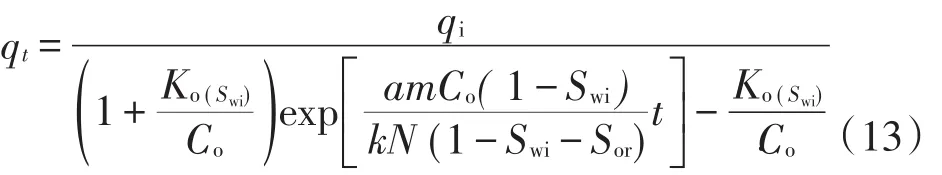
按递减率定义式可知

将(13)式代入(14)式,整理得
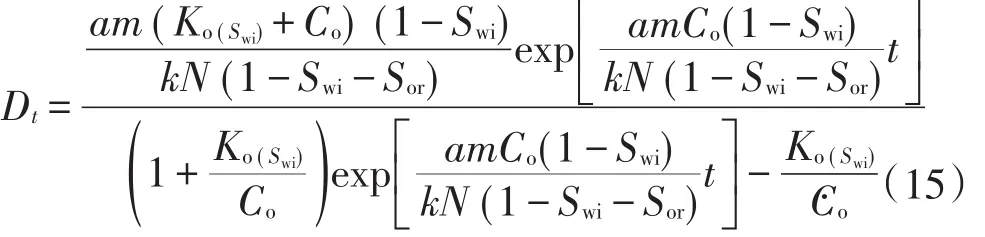

将(16)式代入(13)式,并令 b=-Ko(Swi)/(Ko(Swi)+Co),即可得到标准Logistic产量递减方程:
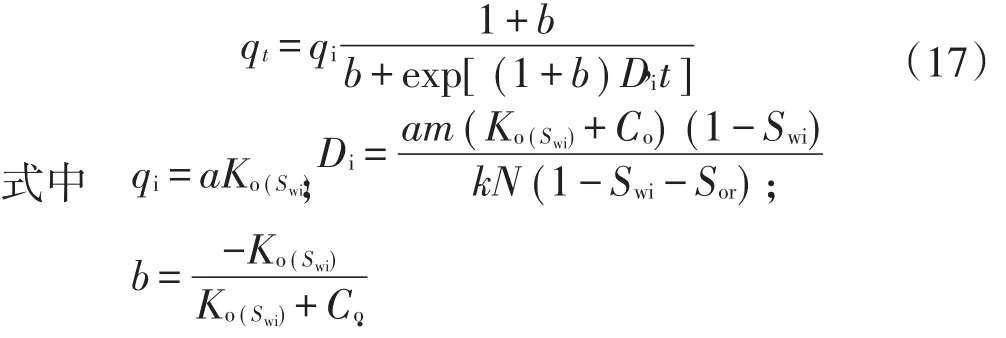
2.2 Generalized-Arc-Tangent产量递减方程
若将文献[2]拟油相相渗关系式中的Swd用Swd替代,则转化为标准的油相相渗关系式:
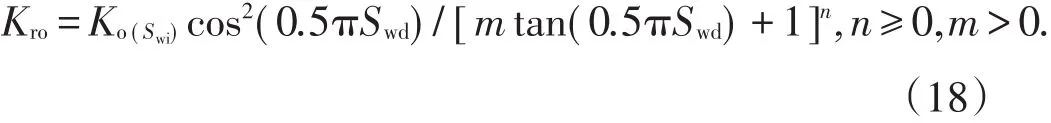
将(7)式和(18)式代入(3)式,取初始条件递减时间t=0时,Swe=Swi,定积分,得
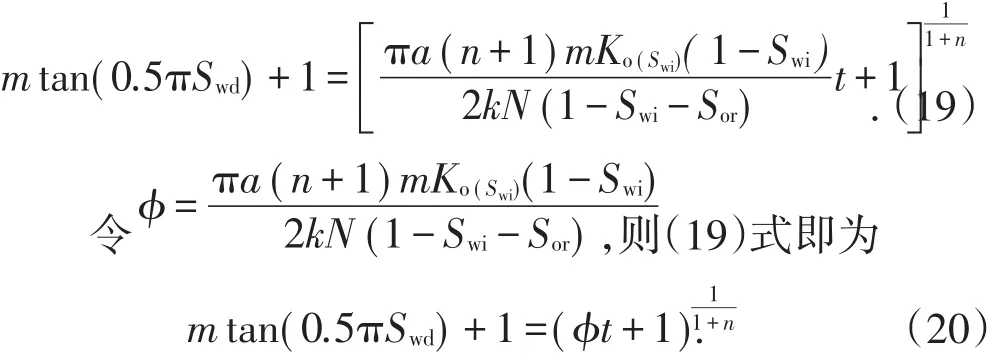
将(20)式代入(18)式,得
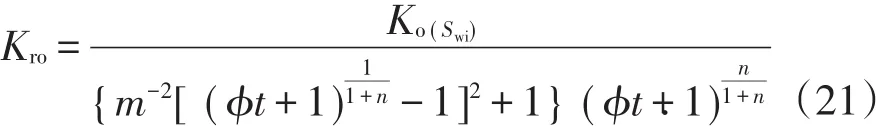
将(21)式代入(2)式,可得Generalized-Arc-Tanent产量递减方程:
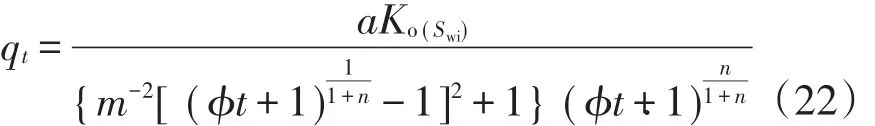
当t=0时,由(22)式可得初始产量:

将(23)式代入(22)式,得

令t=0,由(25)式,得
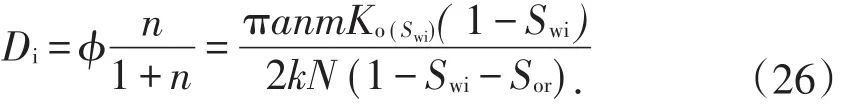
令b=1/n+1,将(26)式代入(24)式,且n>0时,即可得到Generalized-Arc-Tangent产量递减方程标准方程式:
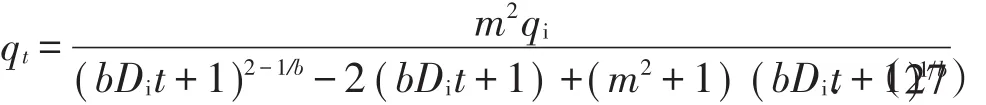
上式中,当t=0时,qt=qi;当t→∞时,qt→0.这些特点,正是描述油气田产量递减函数必须满足的条件,因此,表明上式为一递减函数,可以用于产量递减的分析和预测。由于该函数关系式过于复杂,求解比较特殊,具体求解过程如下。

将实际数据代入(30)式,利用单变量求解方法,可确定出β,z0,z1和z2,进一步利用下式可确定出n,m,φ和qi的值:

虽然Generalized-Arc-Tangent产量递减方程求解方法比较特殊,但该方程既解决一般产量单调递减问题,也能解决产量递减初期曲线向右微凸问题;同时,该方程在一定条件下,可以转化为Arps递减方程、Logistic递减方程和Arc-Tangent递减方程(反正切微分分布产量递减方程)[11]。如:n=0时,令λ=φ/m,那么,(24)式即为反正切微分分布产量递减方程[12]:

按递减率定义式,Arc-Tangent产量递减方程的递减率方程为

令t=0,由(36)式得Di=0.这表明Arc-Tangent产量递减方程是初始递减率为0的一种特殊产量递减方程,其油相相对渗透关系式Kro=Ko(Swi)cos2(0.5πSwd)也很特殊。进一步分析λ的变化对递减率影响来看,随λ的增大,递减率变化歪“几”字形越明显(图1),即递减率初期由0快速增大到某一极值,然后随时间开始缓慢下降,这种特点与Arps递减方程所表现出来的递减率单调下降有着明显的区别[13]。
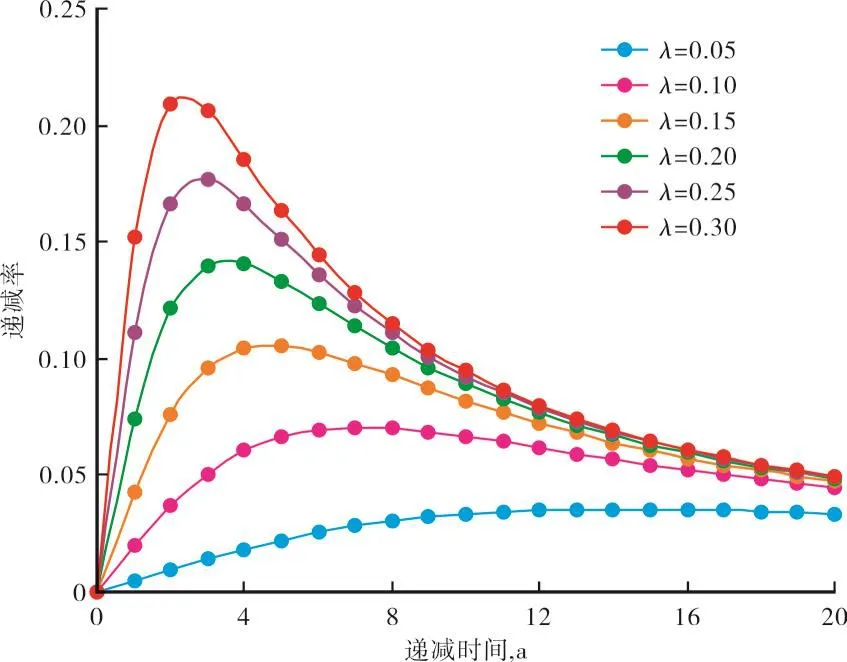
图1 不同λ值下产量递减率变化曲线
3 水相相渗关系式的确定
将(6)式代入(4)式,取初始条件Swe=Swi时,fw=0,定积分得到:

将(37)式代入(5)式,则
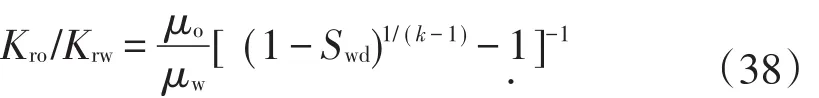
将Logistic和Generalized-Arc-Tangent产量递减方程对应的油相相渗关系式依次代入(38)式,得
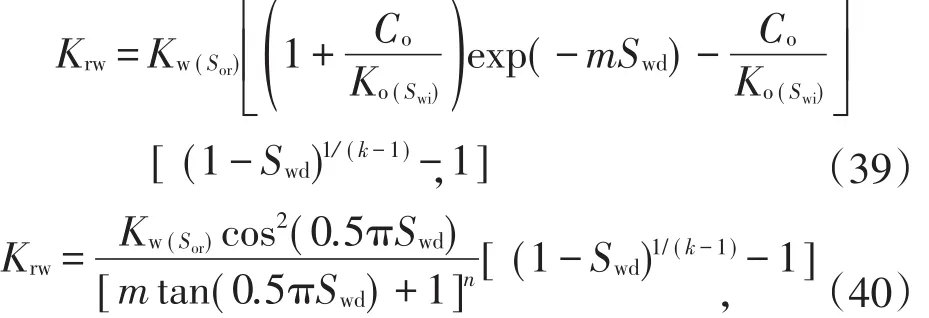
式中 Kw(Sor)=Ko(Swi)μw/μo.
综上所述,对于水驱油田,Logistic和Generalized-Arc-Tangent产量递减方程具有各自特殊的油、水两相相渗关系式[14-18]。
4 实例应用
4.1 丘陵油田陵2北区
1998年以来,丘陵油田陵2北区产量进入连续递减阶段(图2),其单井平均动用地质储量19.2×104t,直接利用Logistic产量递减方程,回归得到该区单井产量递减关系式为

相关系数R=0.996 73;初始递减率Di=0.391 33 a-1;b=-1.223 23.
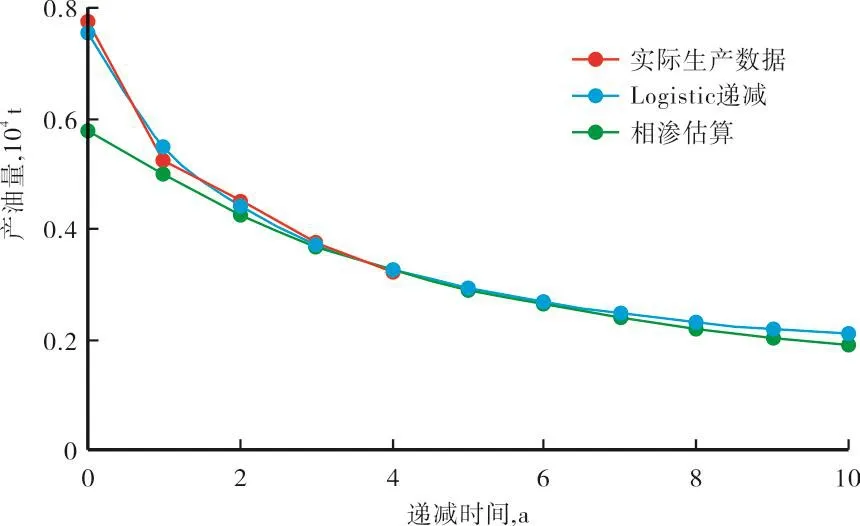
图2 丘陵油田陵2北区产量递减曲线
按文中Logistic产量递减方程对应油相相渗进行拟合(图3)。
Kro=1.025 82exp(-4.559 18Swd)-0.010 74,
(相关系数R=0.999 65),
其中 Ko(Swi)=1.025 82,m=4.559 18,Co=0.010 74.
取初始试采产量为0.584 0×104t,k=0.95,得到初始递减率Di=0.241 50 a-1,b=-0.989 53,这与实际生产数据直接拟合结果一致(图2)。
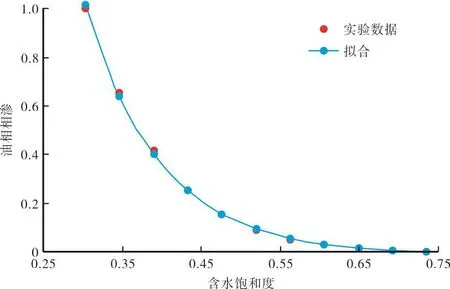
图3 丘陵油田油相相渗曲线
4.2 温五区块
1997年以来,温五区块产量进入连续递减阶段(图4),其单井平均动用地质储量12×104t,直接利用Generalized-Arc-Tangent产量递减方程回归得到温五区块单井产量递减关系式为
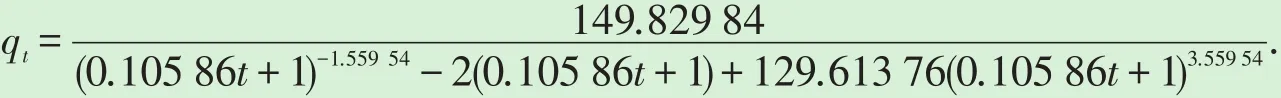
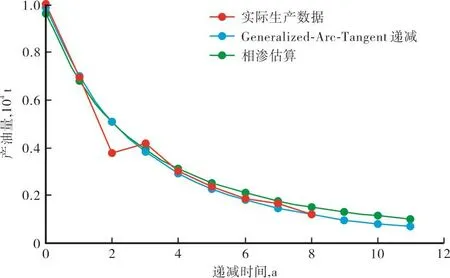
图4 温五区块单井产量递减曲线
拟合相关系数为0.981 82;qi=1.164 96,Di=0.376 81 a-1,m=-11.340 80,n=-1.390 70.
按文中Generalized-Arc-Tangent产量递减方程对应油相相渗进行拟合(图5)。
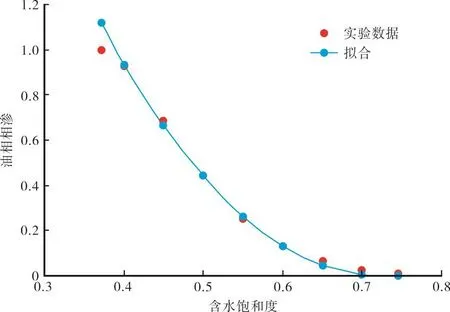
图5 温五区块油水相渗变化曲线
Kro=1.120 90cos2(0.5πSwd)/[2.040 77tan(0.5πSwd)+1]0.76569,
(相关系数R=0.996 55),
其中 Ko(Swi)=1.120 90,m=2.040 77,n=0.765 69.
取初始试采产量为0.912 5×104t,k=0.75,得到初始递减率Di=0.469 24,qi=1.022 82,这与实际生产数据直接拟合结果基本一致(图4)。
上述2个实例应用表明,利用油水相渗确定的递减参数与实际生产数据直接得到的递减参数一致。因此,在油田开发初期或油田开发指标设计时,在生产数据不足的情况下,可利用油井试采资料和油水相渗数据,对产量递减变化趋势进行有效地预估,如利用油相相渗关系式拟合确定出鄯善油田产量递减符合双曲递减、马西深层油藏产量递减符合调和递减、红岗萨尔图油藏产量递减符合指数递减[5],以及本文给出的丘陵油田符合Logistic递减和温五区块符合Generalized-Arc-Tangent递减等。
5 结论
(1)本文完善了Logistic和Generalized-Arc-Tangent产量递减方程的渗流理论。
(2)水驱油田产量递减方程主要受油水两相渗流特征共同决定。
(3)经典的油水两相相渗关系式还无法有效建立Logistic和Generalized-Arc-Tangent产量递减方程。
(4)在生产数据不足的情况下,可利用试采和油水相渗数据对产量递减变化趋势进行有效地预估。
符号注释
a,a0,b,b0,k,m,n,φ,λ,β——待定系数;
Bo——地层压力为p时原油体积系数,m3/m3;
Co——油相相渗修正常数;
Di——初始递减率,a-1或 mon-1;
Dt——t时刻递减率,a-1或 mon-1;
fw——含水率;
h——油层生产厚度,m;
K——油层渗透率,mD;
Ko(Swi)——束缚水饱和度下油相渗透率,mD;
Kro——油相相对渗透率,无量纲;
Krw——水相相对渗透率,无量纲;
Kw(Sor)——残余油饱和度下水相渗透率,mD;
no——开井数,口;
N——地质储量,104t;
Npd——递减期累计产油量,104t;
Δp——生产压差,MPa;
qi——初始递减产油量,t/d;
qt——t时刻产油量,t/d;
re——泄油半径,m;
rw——井筒半径,m;
S——表皮系数;
Swd——归一化含水饱和度;
Swe——出口端含水饱和度;
Swi——束缚水饱和度;
Sˉw——平均含水饱和度;
Sor——残余油饱和度;
t——递减时间,a或mon;
ρo——原油密度,g/cm3;
μo——地层原油黏度,mPa·s;
μw——地层水黏度,mPa·s.

