基于连续小波的地层品质因子计算方法
蒋立,毛海波,刘宏杰,王晓涛,肖艳玲
(中国石油 新疆油田分公司 勘探开发研究院 地球物理研究所,乌鲁木齐 830013)
地震波在传播过程中会发生衰减,高频衰减快,低频衰减慢,其衰减程度与地层品质因子(Q)有关。文献[1]给出了地层品质因子实验室模型;文献[2]首次提出了谱比法,谱比法中频谱比的斜率是地层品质因子的函数;文献[3]提出了从垂直地震剖面(VSP)资料中估计地震波吸收衰减的质心频率偏移法,推导出了地层品质因子和质心频率之间的关系。在地层品质因子计算方法研究上,中国起步较晚,文献[4]使用地震波的频率振幅谱来计算地层品质因子;文献[5]提出了用相邻层地震子波相似系数的相关性来计算地层品质因子的方法;文献[6]提出了用保罗峰值处瞬时频率提取VSP资料的地层品质因子。
地层品质因子的计算方法有谱比法、上升时间法、频移法、振幅衰减法等[7],方法虽多,却不能满足实际应用需求,主要原因如下:①地层品质因子计算同时需要准确的时间和频率信息,而现有的傅里叶变换的频率分析方法需要一定长度的数据,因此很难同时兼顾频率和时间的准确性;②地层品质因子计算需要计算振幅衰减程度,而振幅的衰减是指数级别的,尤其是高频数据,衰减很快,有效振幅的变化范围很大,很小的噪声就会影响地层品质因子计算的准确性。
连续小波变换在时频域具有良好局部化特性和冗余特性[8],可同时准确提取数据的时频信息。使用线性回归分析方法,在不同频率尺度数据中提取振幅指数衰减因子和振幅衰减因子随频率变化的斜率,也可降低噪声对地层品质因子计算的影响。
本文基于连续小波准确提取时频信息,从而提高地层品质因子计算的精度,线性回归分析提高了算法的稳定性,降低了噪声对地层品质因子计算的影响。
1 方法原理
地震波在层状介质中传播时,其振幅呈指数衰减[9],可以用下式表示:
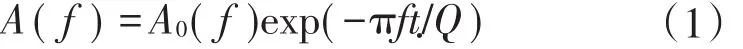
从(1)式可以看出,地震波振幅的指数衰减因子y满足下式:

不同频率的振幅衰减程度不同,高频衰减快,低频衰减慢,因此高频的衰减指数要大于低频的衰减指数。对地震数据做连续小波变换,将地震数据分解到时间-尺度域:
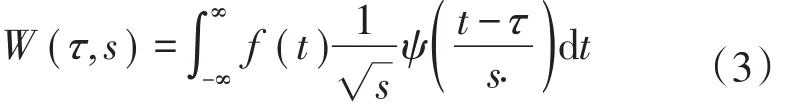
方法测试时选择Morlet小波:

当ω≥5时,ψ(t)在频率域和时间域都有很好的集中性,可以较好地提取时频信息。
为了消除(2)式中时间对地层品质因子计算的影响,针对不同时间-尺度域数据的时间变量t和振幅的指数衰减变量x,用直线x=at+b进行线性回归分析[10]。
为确定回归系数a和b,采用最小二乘法:

E达到最小时,根据极值原理,a与b应满足下列方程:
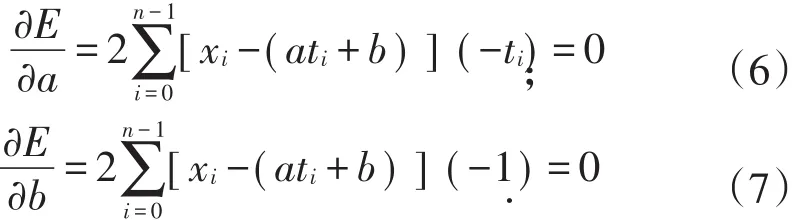
解(6)式和(7)式得:

计算得到的回归系数a就是消除了时间影响的指数衰减因子:

为了消除频率对地层品质因子计算的影响,针对不同时间-尺度域数据的指数衰减因子a和每个时间-尺度域数据的中心频率f,用直线a=kf+c再次进行一元线性回归,可以计算出指数衰减因子随频率变化的斜率k.
计算得到的k就是消除了频率影响的指数衰减因子:

(13)式可变换为

由(14)式可知,地层品质因子可通过指数衰减因子随频率变化的斜率直接计算出来。
总之,地震波的衰减与地震数据的频率、传播时间和地层品质因子相关。通过连续小波时频分析方法对数据进行分频处理,针对各分频数据进行回归分析,得到振幅随时间变化的衰减指数,再对各分频数据的衰减指数进行回归分析,得到最终消除了时间和频率影响的地层品质因子。
2 模型测试
为了检验本文方法的精确度,设计了一个井深为6 000 m的垂直地震剖面下行直达波模型(图1),每隔1 000 m地层品质因子发生一次变化,1 000 m,2 000 m,3 000 m,4 000 m,5 000 m和6 000 m井深对应的地层品质因子分别为80,300,150,60,200和400.由于该模型主要用于检验地层品质因子的计算精度,与地层速度无关,故各地层的速度设为常速2 000 m/s.

图1 经过6层地层品质因子衰减的垂直地震剖面直达波模型
分别利用连续小波地层品质因子计算方法、频移法和谱比法对该模型进行计算,计算出的地层品质因子与模型地层品质因子见图2.从图2可以看出,在0~1 000 m时,3种方法计算出的地层品质因子都比较准确;随着深度增加,地震波衰减程度越来越高,频率变低,频移法计算出的地层品质因子误差变大,出现震荡,谱比法计算出的地层品质因子比较准确;但到5 000~6 000 m时,误差大于连续小波地层品质因子计算方法,利用连续小波地层品质因子计算方法计算出的地层品质因子与模型地层品质因子的误差小于10%.总之,连续小波地层品质因子计算方法的准确性和稳定性高于谱比法和频移法。
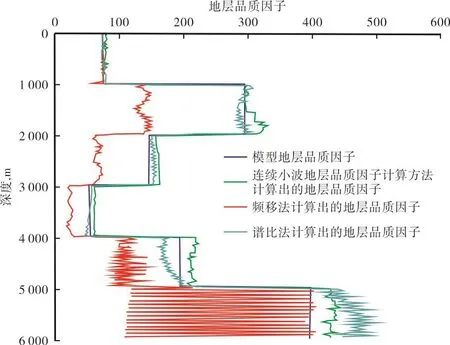
图2 模型地层品质因子与3种方法计算出的地层品质因子对比
3 实际应用
选择准噶尔盆地石南地区的石306井零偏垂直地震剖面资料(图3)进行地层品质因子的计算。石南地区白垩系岩性油气藏[11]对地震资料分辨率要求较高,因此在该地区研究地层品质因子提取技术比较有意义。

图3 准噶尔盆地石南地区石306井零偏垂直地震剖面资料Z分量数据
在利用垂直地震剖面资料进行地层品质因子计算的过程中,首先准确拾取下行初至波时间,然后利用连续小波变换将数据分解为不同频率的时间-尺度域,分别计算各尺度域数据振幅对数随初至时间变化的指数衰减因子,然后再计算指数衰减因子随频率变化的斜率,最终求取地层品质因子。
在地层品质因子求取过程中,使用了分段多点回归方法计算不同时间段的地层品质因子,同时,根据数据的质心频率,合理减少小波变换的尺度个数,降低振幅变化的动态范围,提高了地层品质因子计算的精度。与频移法和谱比法进行比较(图4a),连续小波地层品质因子计算方法计算出的地层品质因子稳定性更高,与垂直地震剖面层速度曲线(图4b)相比,变化总趋势基本一致,随着深度的增加,由低到高,但也有不一致的地方,如1 600 m附近有个突变点,而层速度曲线上没有。
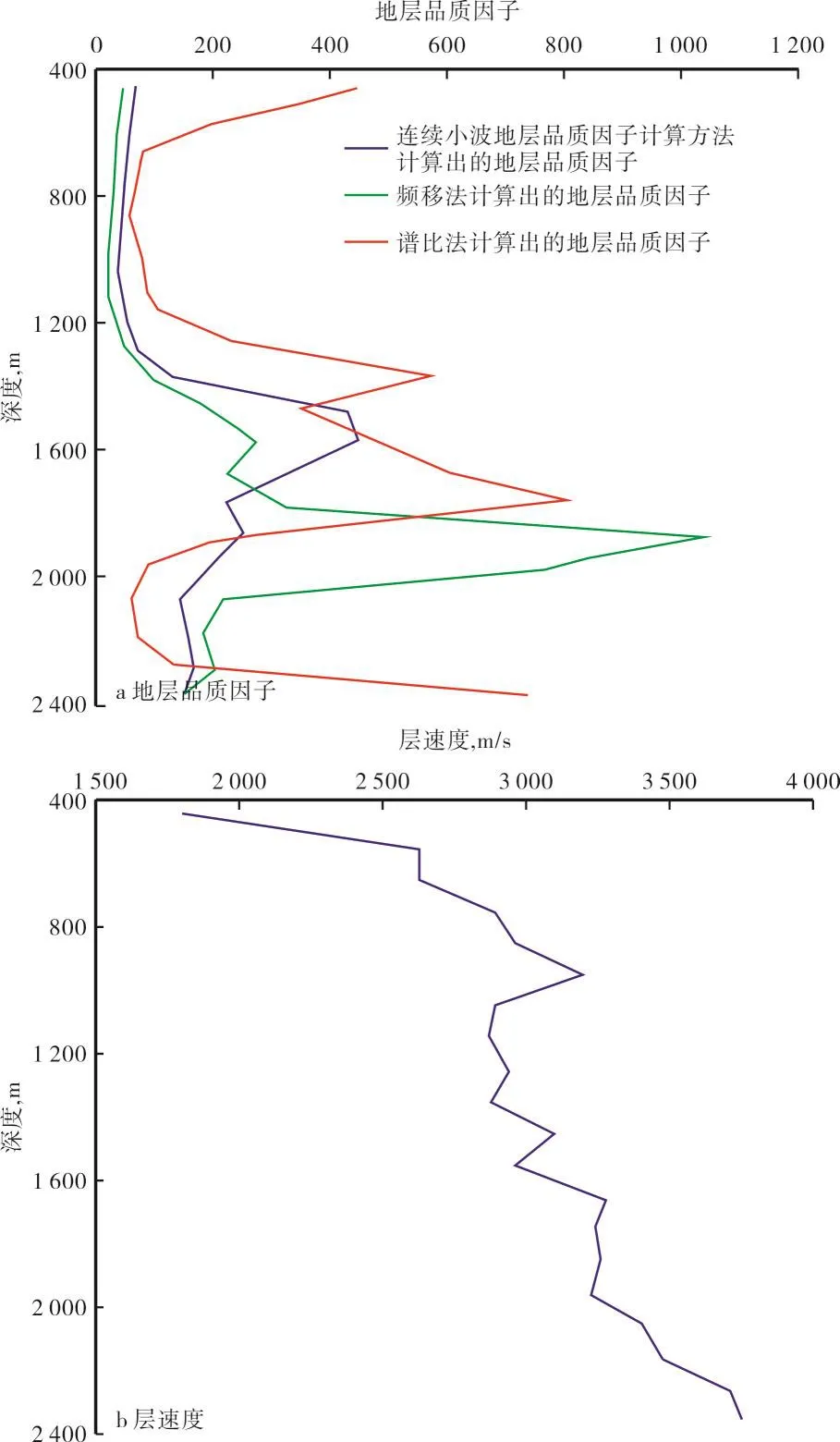
图4 准噶尔盆地石南地区石306井垂直地震剖面资料计算的地层品质因子随深度的变化曲线以及垂直地震剖面层速度曲线
目前,近地表地层品质因子主要使用微测井方法来测量,在准噶尔盆地玛湖地区野外采集了一口微测井数据(图5),激发点井深为39.0 m,地表摆设了18个检波器,与井的距离为1.5~47.5 m.
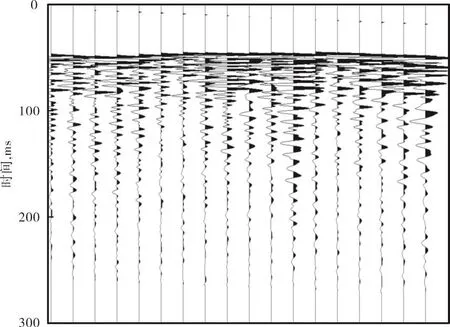
图5 准噶尔盆地玛湖地区微测井数据
微测井数据的地层品质因子计算过程与垂直地震剖面类似,也需要拾取初至波时间,计算初至时间与振幅的指数衰减因子,然后计算出最终地层品质因子(图6)。
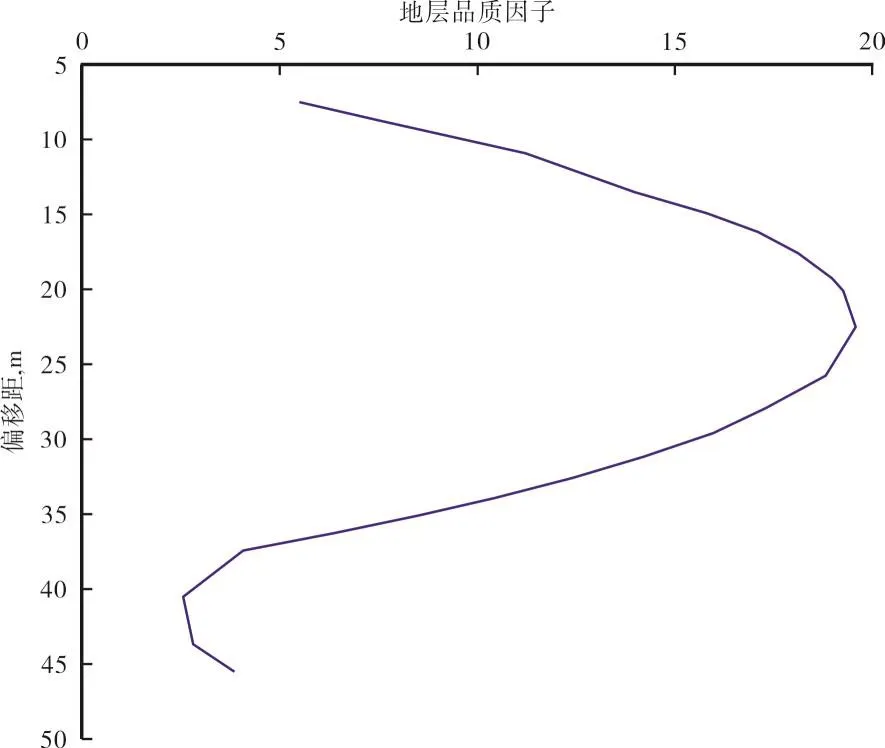
图6 准噶尔盆地玛湖地区微测井数据计算的地层品质因子
采集微测井数据点的近地表为双层结构,1.0~5.0 m为低速层,5.0~38.0 m为降速层。离井7.5 m处计算出的地层品质因子为6.7,反映的是低速层和降速层的等效地层品质因子,因为地震波分别在低速层和降速层传播。离井22.5 m的地层品质因子为24.4,反映了降速层的地层品质因子,因为此处大部分地震波在降速层中传播。离井45.5 m的地层品质因子为4.9,反映了低速层的地层品质因子,因为此时大部分地震波在低速层中传播。
地震数据的地层品质因子计算方法与垂直地震剖面和微测井有所不同,在选择振幅和时间时主要选择峰值处的振幅和时间,这样用回归方法计算地层品质因子时,需要选择较大的时窗才能满足回归方法所需的计算点数,对于低频的尺度域数据,所需的时窗长度就要更大。因此,计算出的地层品质因子时间间隔较大,如果要计算每个样点的地层品质因子,则需要使用插值方法。
另外,由于地震数据含有一定的噪声,会影响地层品质因子的计算精度,为了减少噪声的影响,使用中值滤波方法沿空间方向对计算出的地层品质因子值进行平滑处理,得到最终的地层品质因子(图7)。
4 结论
(1)连续小波变换在时频域具有良好的局部化特性和冗余特性,可同时准确提取数据的时频信息。因此计算出的地层品质因子准确性更高。
(2)在地层品质因子计算过程中,使用回归分析方法降低了地震数据中噪声对地层品质因子计算的影响。
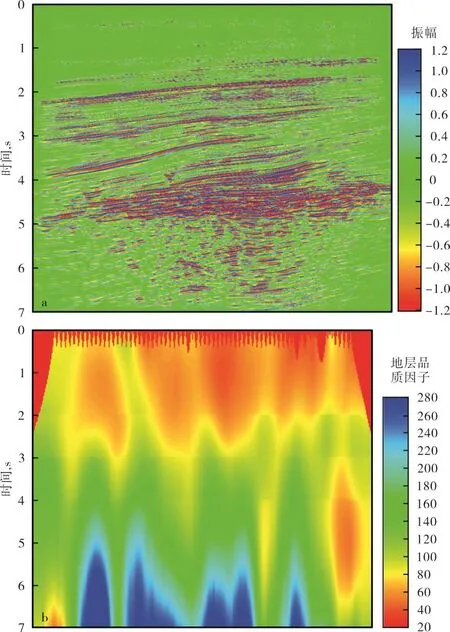
图7 准噶尔盆地玛湖地区地震剖面(a)和地震数据计算出的地层品质因子剖面(b)
(3)连续小波地层品质因子计算方法具有较高的灵活性,可应用于垂直地震剖面、微测井和地震数据的地层品质因子计算。同时在地层品质因子计算时也可应用中值滤波降低噪声的影响,还可以通过计算质心频率减少连续小波变换的尺度个数,从而减小地震波振幅的范围来提高地层品质因子计算的精度。
(4)连续小波地层品质因子计算方法利用分频处理方法,分频的频带宽度采用倍频程方式,高频段的频率间隔较大,从而会降低地层品质因子计算的精度。
符号注释
a,b,c——回归系数;
A(f)——衰减后振幅谱;
A0(f)——衰减前振幅谱;
E——能量误差;
f——频率,Hz;
f(t)——地震信号;
i——离散点序号;
k——消除了频率影响的指数衰减因子;
n——离散点个数;
Q——地层品质因子;
s——尺度因子;
t——地震波传播时间,s;
W(τ,s)——地震信号的小波变换系数;
τ——小波域时间变量;
ψ(t)——小波函数;
ω——常数。

