某农用车车架的模态分析与优化

陈 棕 ，李尚平 ，郑海腾 ，李 冰

（1.广西科技大学 机械工程学院，广西 柳州 545000；2.广西民族大学 化学化工学院，广西 南宁 530006；3.钦州学院 机械与船舶海洋工程学院，广西 钦州 535000）

1 引言

车架是发动机、底盘和车身中各主要总成的安装基体，车架在农用车辆可靠性方面起着举重若轻的作用，车架承受这些总成的质量及其传给它的各种力和力矩。车架设计的合理性直接影响到农用车在使用过程中的可靠性和安全性。由于农用车的工况十分的恶劣，再加上经常超载等不规范使用，导致车架在使用过程中容易产生裂纹甚至断裂的情况，这也给买车的人们带来了极大的安全隐患。

目前解决此类问题最有效的措施是将有限元方法、实验科学技术和优化设计相结合起来对车架进行频率、位移、应力等性能分析和局部优化。结合常见车架断裂的因素，这里利用有限软软件分析的自由模态结果，再结合模态实验获取的模态参数进行对比分析，找到车架断裂的原因，在根据分析结果采取合适的优化方法和正对性的结构改进，最终从根本上解决此类问题。

2 车架有限元模型的建立

2.1 有限元模态分析理论

自由模态分析是研究物体在不受外界载荷和约束的条件下求解其有限个自由度的运动矢量。由振动学理论转化为数学模型为：

式中：M、u¨、C、u˙、K、u—质量矩阵 、加速度向量、阻尼矩阵、速度向量、刚度矩阵、位移向量。

对于处于无阻尼自由振动系统，其相关运动微分方程为：

式中：ω2—特征值（固有频率的平方）；μ—特征向量（即振型）。

模态分析的目的是为了获取物体的相关模态参数，这就需要求解方程（2）中的特征根

ωi（i＝1，2，…，n），然后得到物体的自由模态和振型。其中无阻尼自由振动的特征方程表示为：

2.2 有限元模型的建立

现在以某型号的低速运载农用车车架为研究对象，车架主体由左右分开的2根纵梁和与之相连的9根横梁组成，纵大梁断面采用凹槽等截面设计。组成车架的零件可以看做是外形规则的薄板构建，所以在导入车架的三维模型后，先对车架进行中面的抽取，以减少模型的计算容量。为了让有限元软件划分的网格能更好的满足分析的需求，首先对车架的三维模型做如下处理：

（1）删除直径小于16mm的定位孔和工艺孔，保留部分螺栓连接孔；

（2）去除8 mm以下的圆角；

（3）删除一些对于模态分析影响较小的零部件，例如局部的小孔、板簧吊耳、储气筒和蓄电池支架等。

模型网格的划分是整个模态分析最为重要的一个环节，网格的质量将会直接影响到最后的计算结果，一般网格划分的越细，单元网格的数量越多，网格的质量会越高，这里结合计算机的运算水平和车架的实际尺寸，选取单元大小为（5～15）mm以内，对局部结构复杂的地方采取手动划分来提高网格质量。车架模型完成划分网格后的单元总数74474个，节点总数为77288个，板壳结构的材料相关属性为：弹性模量E=2.07e5MPa、泊松比μ=0.3、密度ρ=7.83e-9t/mm3。车架完成网格划分后的模型，如图1所示。

图1 划分网格后的有限元模型Fig.1 Mesh Finite Element Model

3 车架的理论模态与试验模态

3.1 车架的自由模态分析

对车架采取无边界约束的自由模态分析，通过有限元软件Hyperworks中自带的Radioss求解器求得车架在无边界约束情况下的固有频率和振型。由于前六阶为车架的刚体模态，频率值接近于0Hz，故从第七阶开始算起作为车架的第一阶频率，得到车架模型的前四阶模态和振型，如表1所示。

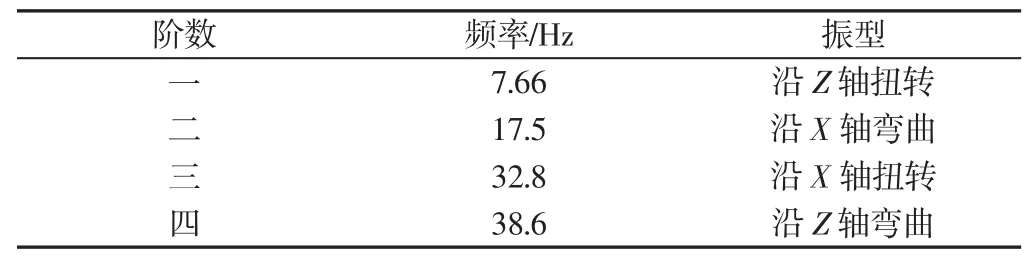
表1 车架的前四阶模态分析Tab.1 Modal Analysis of the Front of the Vehicle Frame

图2 车架前四阶振型图Fig.2 The First Four Order Modes of the Frame

3.2 车架的模态实验

模态实验是通过LMS采集前端采集信号，得到车架在受到冲击力的情况下输入与输出函数，通过曲线拟合方法识别出结构中的模态参数。通常情况下，理论模态与试验模态之间是一定会存在误差的，所以在得到两组模态数据之后，需要将两组数据进行数据分析，若分析结果表明误差较小，则可以证明所采取的模态算法和有限元模型均符合实际情况，则所得到的数据将能直接被用于以后的结构优化中去，不需要每次对产品结构做出改动都要进行相关的试验分析，这也大大节约了成本、缩短了产品开发周期，同时也使得优化设计变得更加简单。车架的模态实验图，如图3所示。

图3 车架模态实验图Fig.3 Experimental Model of Frame

3.3 理论模态与试验模态的对比

通过模态实验获取的车架前四阶阵型图（第二阶模态丢失），如图4所示。

有限元软件的计算结果与实验所得到结果对比，如表2所示。通过表2可以很直观的看到两组数据的值，它们的误差在10%左右，考虑到实验受到环境，设备等因素的影响，10%左右的误差基本符合实验误差，故本次实验所得到的数据比较有参考价值。

表2 理论模态与试验模态的对比Tab.2 Comparison of the Oretical and Experimental Modes

3.4 模态结果分析

4 车架的优化设计

根据上面的分析结果，我们可以采取提升发动机悬置节点的动刚度或改变车架局部结构来避开发动机在怠速状态下的频率范围，这里依据拓扑优化结果改变车架的结构来提升车架的第二阶模态频率。

4.1 拓扑优化原理

随着有限元技术的不断发展，拓扑优化作为一种新突起的结构设计方法，主要被用来研究不受形状（或大小）改变影响的固态物体或几何模型。通过这种技术，我们能使物体的力学性能、质量、形貌等获得提升。拓扑优化的三要素分别是设计变量、约束函数和目标函数，优化设计的目标就是要求运用所选的设计变量使目标函数达到实际范围内的最佳值。用数学模型可以简化表示为：

对于结构的优化设计，常见的有离散结构的拓扑优化和连续体结构的拓扑优化，这里采用的优化方法为连续体结构拓扑优化中应用比较精确的变密度法，同时变密度法也是一种利用普遍的拓扑优化方法，属于材料（物理）分析方法。变密度法以连续变量的密度函数来研究单元的相对密度和材料弹性模量之间的相互作用，这种研究方式以各向同性材料为基础，人为的假设相对密度与材料弹性模量的某种对应关系，极大的减少了均匀化和增加微观结构的过程，使程序中整体结构变得简略并且易于计算。目前重要应用在变密度法中经常使用的插值模子类型有：Solidisotropic Microstructures with Penalization（简称为SMP）和Rational Approximation of Material Properties简称为RAMP）。这两种方法都是采取对中间变量的约束，使中间密度值向（0～1）两端收缩，使拓扑优化模型由连续变量朝（0～1）单元密度的离散变量逼近，此时与中间密度单元相对应的弹性模量则变得非常小，几乎对结构的刚度矩阵不产生变化[8]。

4.2 车架的拓扑优化

拓扑优化概括来讲就是在满足所给约束的条件下，设计出适当的结构尺寸和合理的结构形式，在设计区域内产生优化的形状和材料分布，根据优化后的形状和材料的分布确定出物体的最优几何结构，基本思想就是以单元密度为媒介，把结构优化问题转化成了寻求最优材料分布问题。拓扑优化在不需要人为的设置优化参数的前提条件下自动的将材料分布作为优化的参数。在进行拓扑优化分析前，根据所建立的有限元模型施加相应的边界条件和载荷，确定优化目标，定义约束函数，最后根据单元密度分布图有针对性的进行结构设计和改进。

这里采用Hperworks中自带的模块Optistruct对车架进行拓扑分析。根据有限元的模态分析结果我们可以得出车架的应力主要集中在中部和两端，车架的零件也主要分布在这些区域，而车架的其它位置则十分的空旷，这给车架进行结构改进提供了可靠的设计区域，所以首先在有限元软件中对车架空旷的地方进行填补，填补后的图形，如图5所示。定义填补区域料分布为优化设计变量，以提高车架第二阶频率为目标函数，车架结构体积分数作为约束条件进行拓扑优化。

图5 拓扑优化模型Fig.5 Topology Optimization Model

4.3 对车架优拓扑结果的分析与结构改进

将体积比设置为0.35，即消减材料65%以上，对车架进行拓扑分析，拓扑优化结果显示的单位密度分布图，如图6所示。

图6 优化结果单位密度分布图Fig.6 Unit Density Distribution Optimization Results

通过对拓扑优化结果的分析，我们在对车架结构进行改进时需要考虑以下两点：

（1）根据图6的单元密度云图我们可以清晰地看出车架密度为1的地方主要集中在中部和两端的地方，也就是说，这些地方对强度的要求很高，所以再改进车架结构的时候需要重点考虑这些地方。

（2）优化关心的目标是车架的第二阶模态频率，从车架的阵型图可以看出车架的第二阶阵型弯曲的部分主要集中在车架的中间位置，这与单元密度云图中应力集中的地方相一致，故对中间位置的结构改进将是提高第二阶频率的关键。

将上面的车架拓扑优化结果分析作为参考，再结合车架设计的相关准则和实际生产加工等因素，在车架的设计区域增加了3根横梁，其宽度与原有车架梁宽度保持一致，改进后的车架形状，如图7所示。

图7 结构改进后的车架图Fig.7 Frame Diagram of Improved Structure

4.4 对优化方案的验证

按照之前计算车架自由模态的方法和流程，重新对优化后的模型进行计算，经过对比发现车架的前四阶模态均有不同程度的提高，尤其是最关注的第二阶模态，在优化后得到的频率为20.0Hz，相比优化前的频率提高了14.29%，成功的避开了车架发动机在怠速状态时的频率范围，取得了比较理想的结果。新模型的振型以及频率对比，如图8所示。

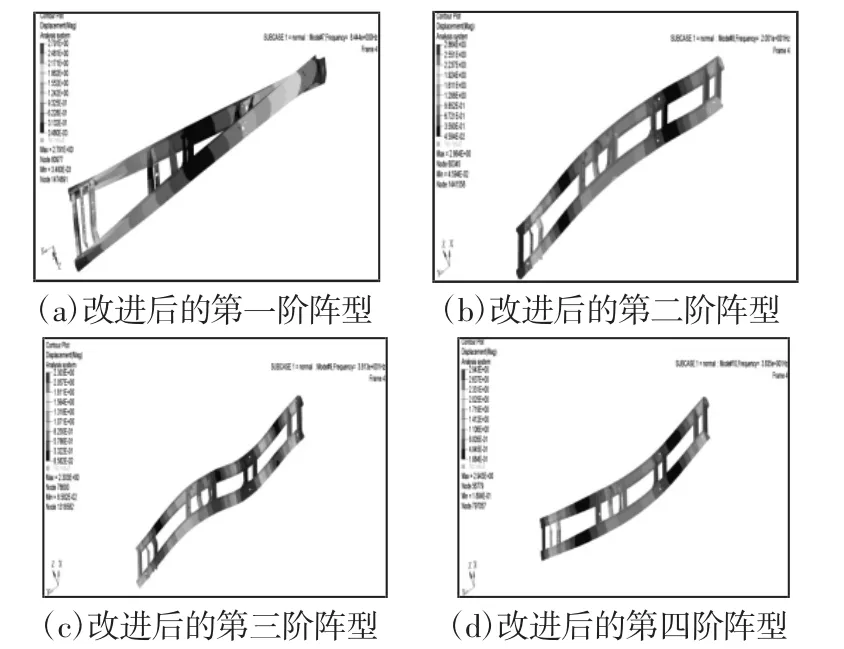
图8 优化后车架的前四阶振型Fig.8 Optimization of the First Four Order Modes of the Rear Frame

对优化结果的分析，如表3所示。

表3 对车架优化结果的分析Tab.3 Analysis of the Optimization Results of Frame

5 结论

以某型号的低速载货的农用车车架作为研究对象，对车架的自由模态采取了理论分析和试验分析。分析结果显示车架断裂的主要原因在于车架二阶频率与发动机怠速状态时的频率值十分接近。故对车架采取提高二阶频率为目的的拓扑优化，最后根据优化结果对车架进行结构上的改变。在整个过程中，我们可以得到的结论有：

（1）通过对比车架的理论模态和试验模态，两者相差10%左右，考虑到环境因素，10%的误差在可以接受的误差范围以内。结果充分验证了车架有限元模型的正确性，同时本次实验所获得数据也有着非常高的参考价值。

（2）参照拓扑优化的结果，对车架进行针对性的改改良以后。又对新的模型进行验证，验证结果表明与发动机怠速频率最为接近的第二阶频率也有了很大的提升，故优化的结果达到了之前的预想。同时本次研究所采用的方法和流程将会给今后汽车行业解决此类问题作出相应的参考。