非对称钝尾缘翼型气动噪声数值研究
詹枞州, 叶 舟,2, 张俊伟, 宋建业
(1. 上海理工大学 能源与动力工程学院, 上海 200093;2. 上海市动力工程多相流动与传热重点实验室, 上海 200093)
近年来,化石燃料燃烧和温室气体排放导致全球变暖,促使各国积极探寻清洁高效的可替代能源[1-2]。风能作为一种可再生能源,因其储量丰富、温室气体零排放等优势逐渐得到广泛关注和政策支持[3-4]。随着风电产业的不断发展,越来越多的风力发电机组建在风力资源充沛的地区,但风力机运行过程中产生的噪声污染极大[5]。Mohamed[6]对133个风电场附近居民进行调研,发现20%的风电场不同程度地影响附近居民生活。Nii等[7]研究发现噪声已成为风电场选址建厂时必须关注的主要问题之一。风电机组的噪声主要包括机械噪声和气动噪声[8]。机械噪声主要是由于机械设备运转时不同部件之间摩擦力或非平衡力导致无规律振动引起的[9];气动噪声主要是叶片与塔架的干涉和流体湍流脉动等引起的[10]。其中,机械噪声随材料的发展大幅度降低,气动噪声成为风力机噪声的主要声源[11]。翼型自噪声是风力机气动噪声的主要来源,包括湍流边界层尾缘噪声和钝尾缘噪声等5种,而尾缘噪声占翼型自噪声的主导地位[12]。因此,研究尾缘噪声对风电的应用和普及意义重大。
国内外学者针对尾缘噪声进行了大量的实验和数值模拟。Singer等[13]利用混合法对NACA翼型进行数值模拟,发现翼型尾缘边界层与翼型尾缘相互作用引起的尾缘脱落是产生噪声的主要原因。刘雄等[14]研究了不同厚度的风力机翼型尾缘对翼型气动性能的影响,发现适当增加翼型尾缘厚度会提高气动性能,但未对气动噪声进行深入研究。Ewert等[15]利用大涡模拟和声学扰动方程联合求解的方法对风力机尾缘噪声进行数值模拟,计算结果与实验值比较符合,但缺乏针对尾缘涡脱落问题的研究。Ikeda等[16]对不同弦长下的翼型尾缘噪声进行了数值模拟。Lummer等[17]研究了对称翼型在0°攻角下的气动噪声,发现尾缘脱落涡会对声学信号产生影响。Jones等[18]对对称翼型不同攻角下的自噪声进行了数值模拟,发现翼型自噪声与尾缘脱落涡的剪切作用密切相关,尾缘脱落涡越明显,产生的气动噪声越大。
笔者基于分离涡模拟方法(DES)和声学类比方程建立了噪声预测方法。针对非对称翼型S809进行样条函数参数化处理,研究不同尾缘厚度及其分配比对风力机翼型气动性能和气动噪声的影响。
1 模型方程
1.1 湍流模型
DES方法是Spalart等[19]提出的混合模拟法,即在近壁面采用雷诺平均N-S方程(RANS)方法模拟,在远离壁面的主流区域采用大涡模拟(LES)方法模拟。
Spalart-Allmaras方程模型的积分形式为:
(1)
(2)
(3)
(4)
基于Spalart-Allmaras方程模型的DES方法是将长度尺度d替换为:
(5)
式中:Δ为流场中x、y和z方向的网格最大值,Δ=max(Δx,Δy,Δz);CDES为常数,CDES=0.65;dw为网格中心到壁面的距离。
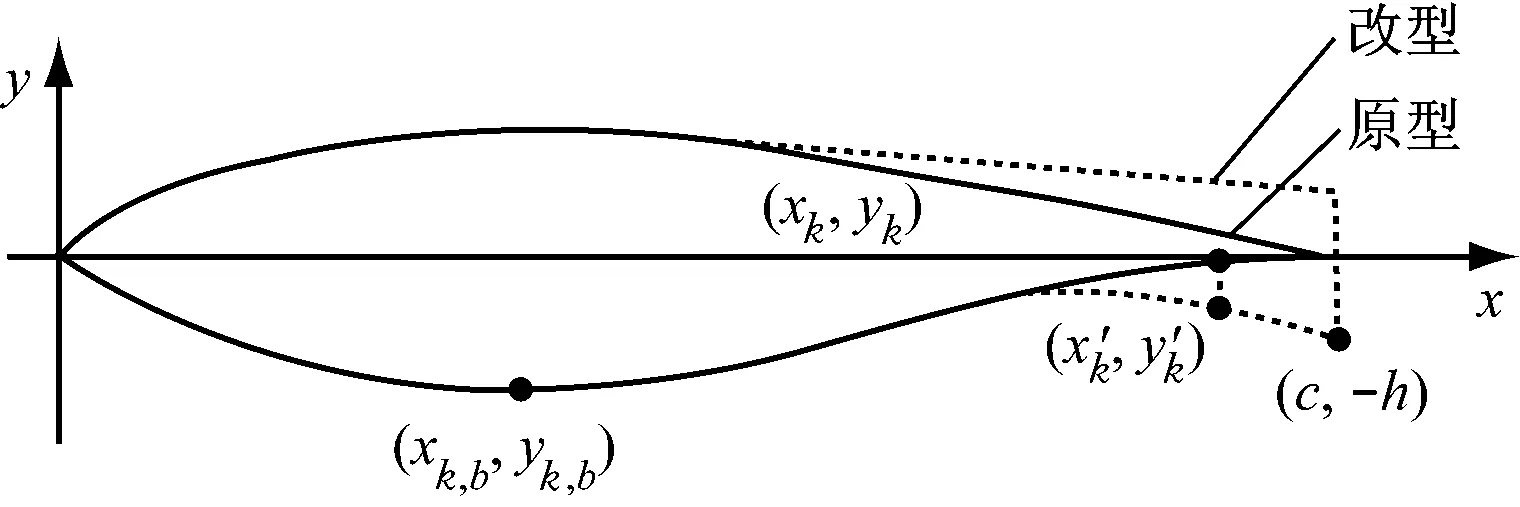
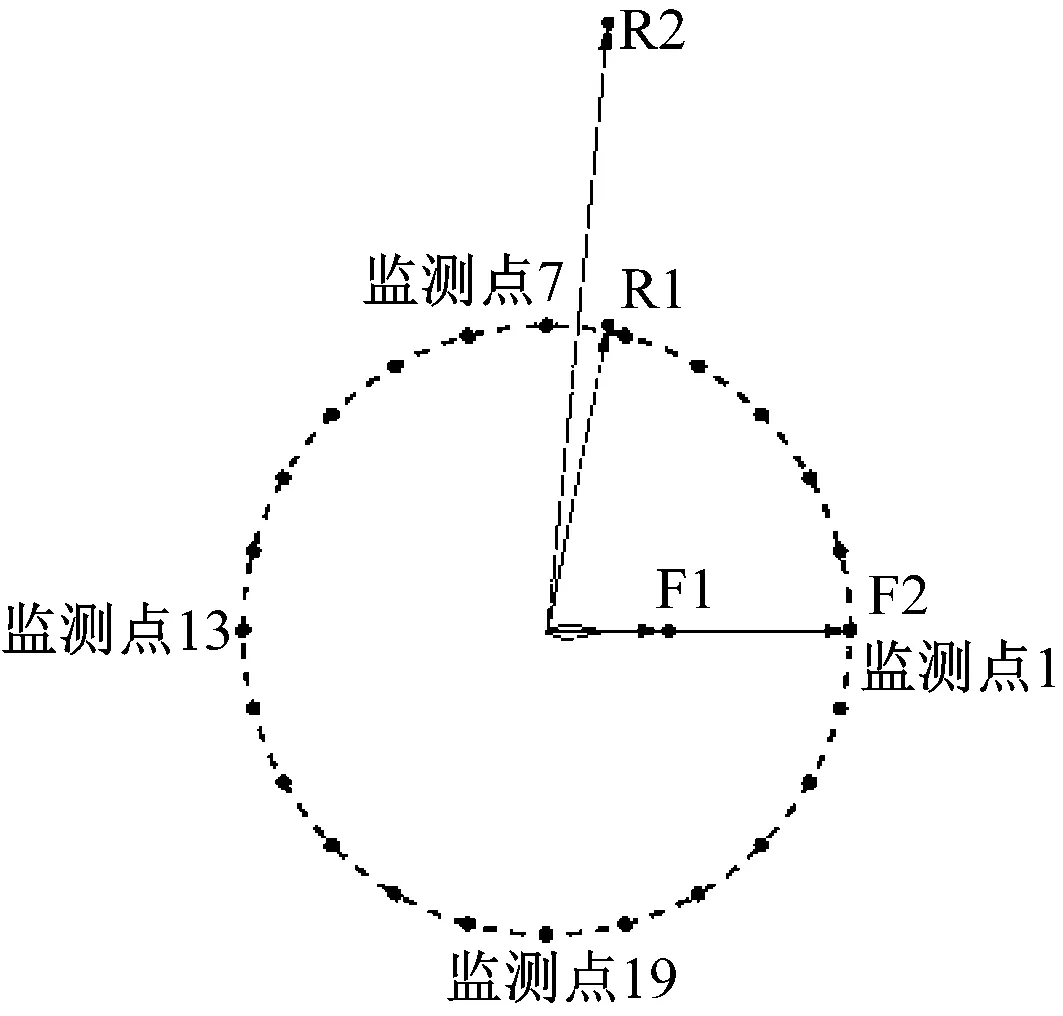
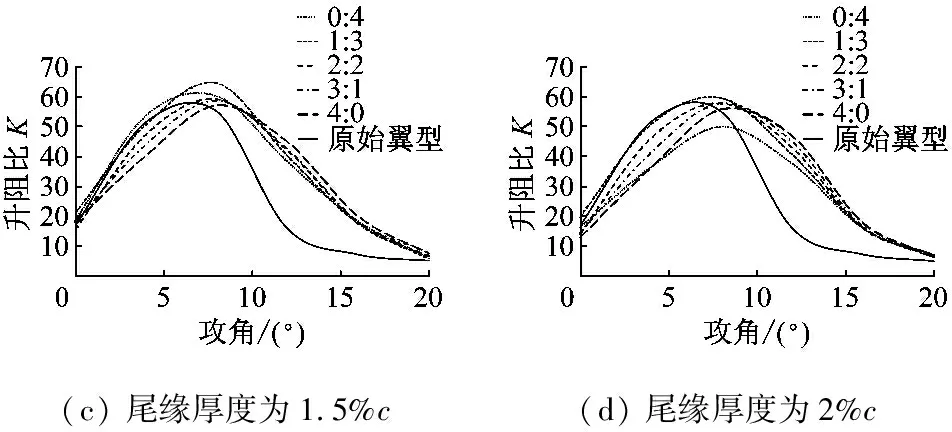
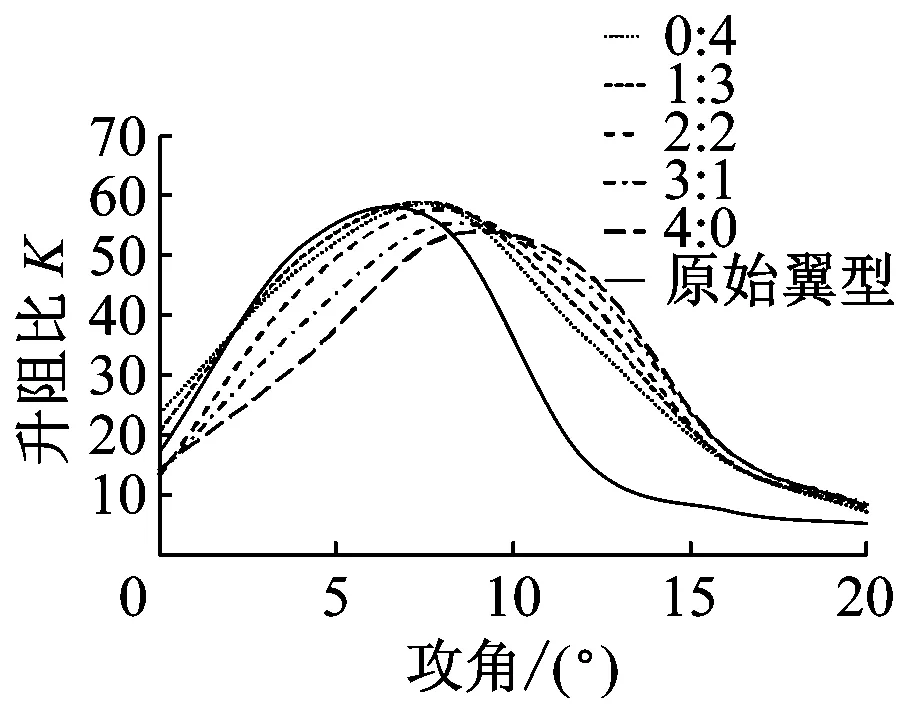
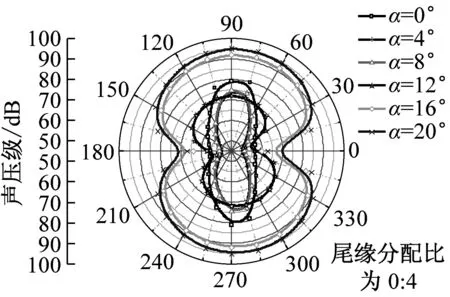
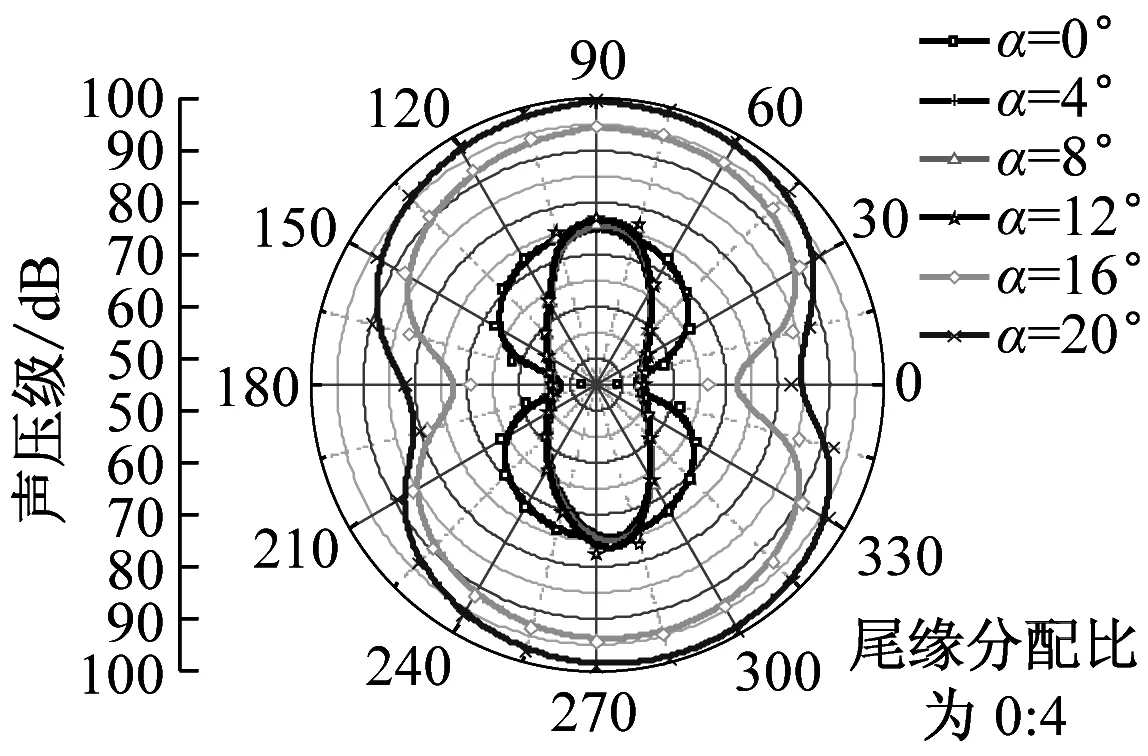
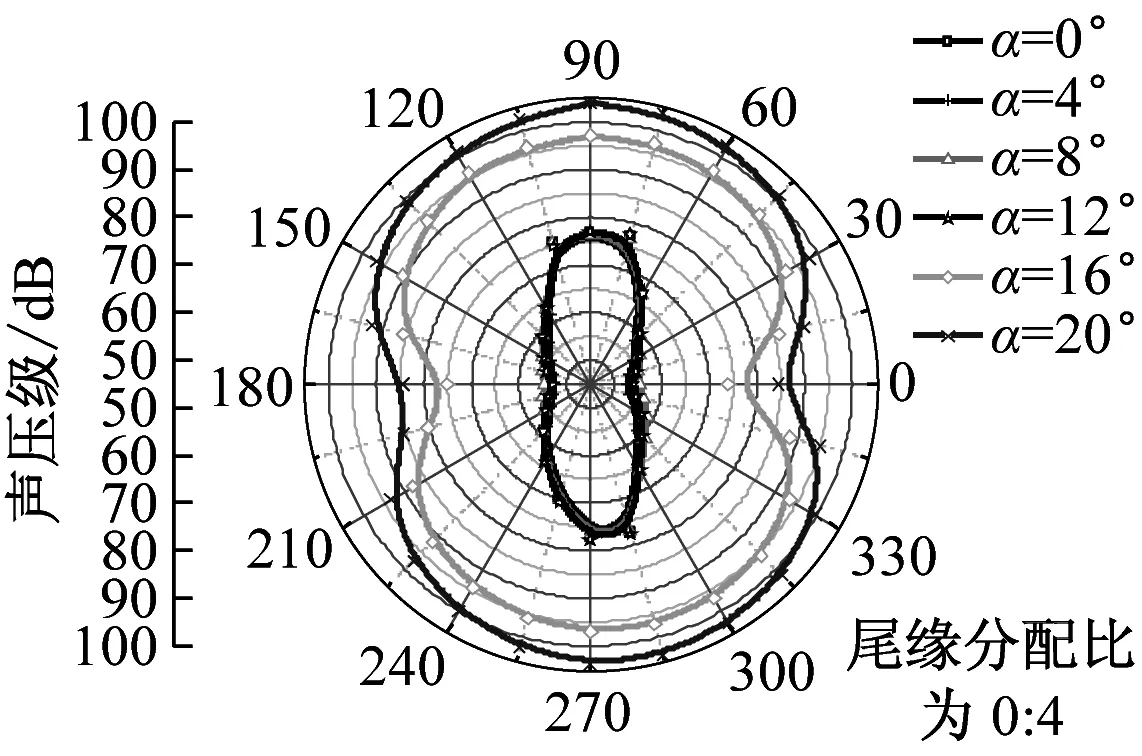
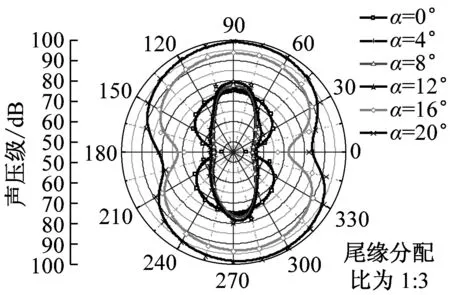
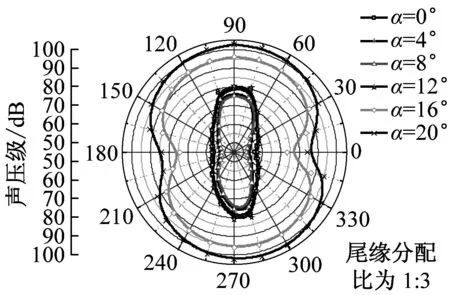
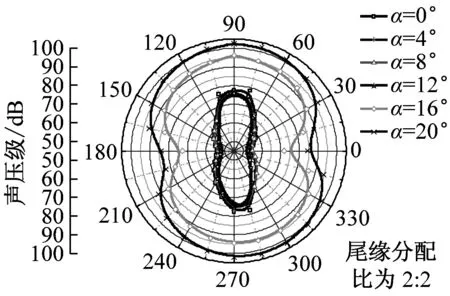
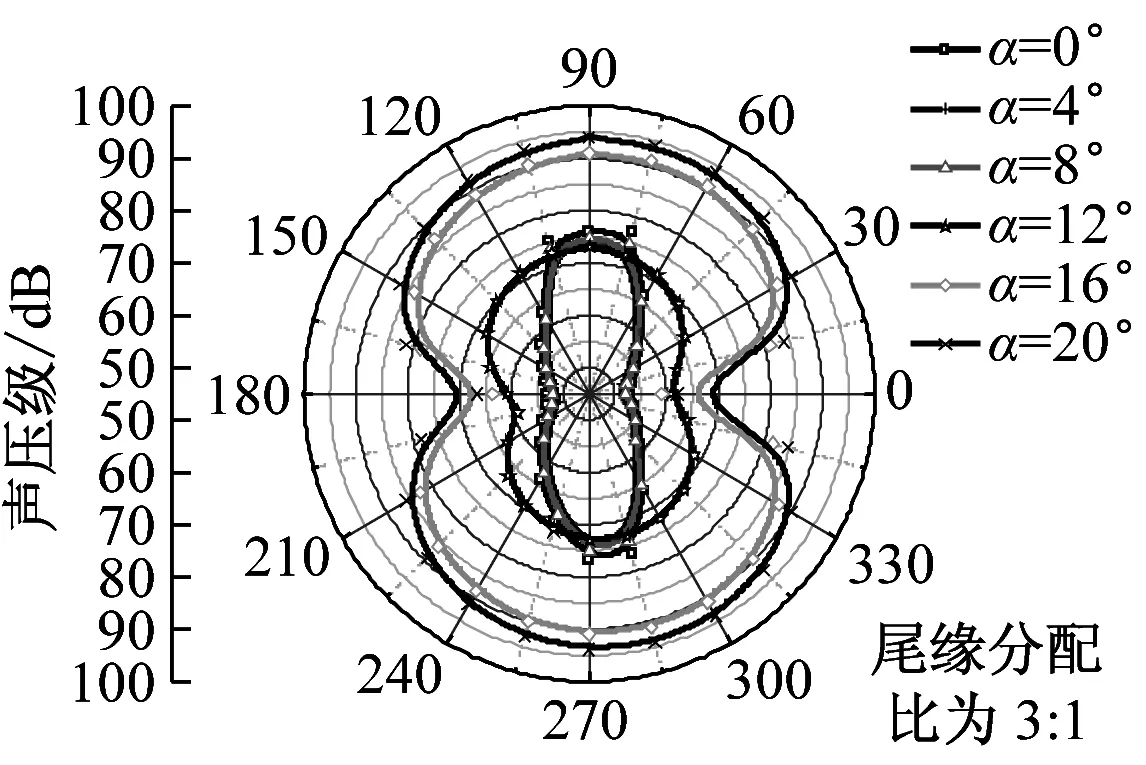
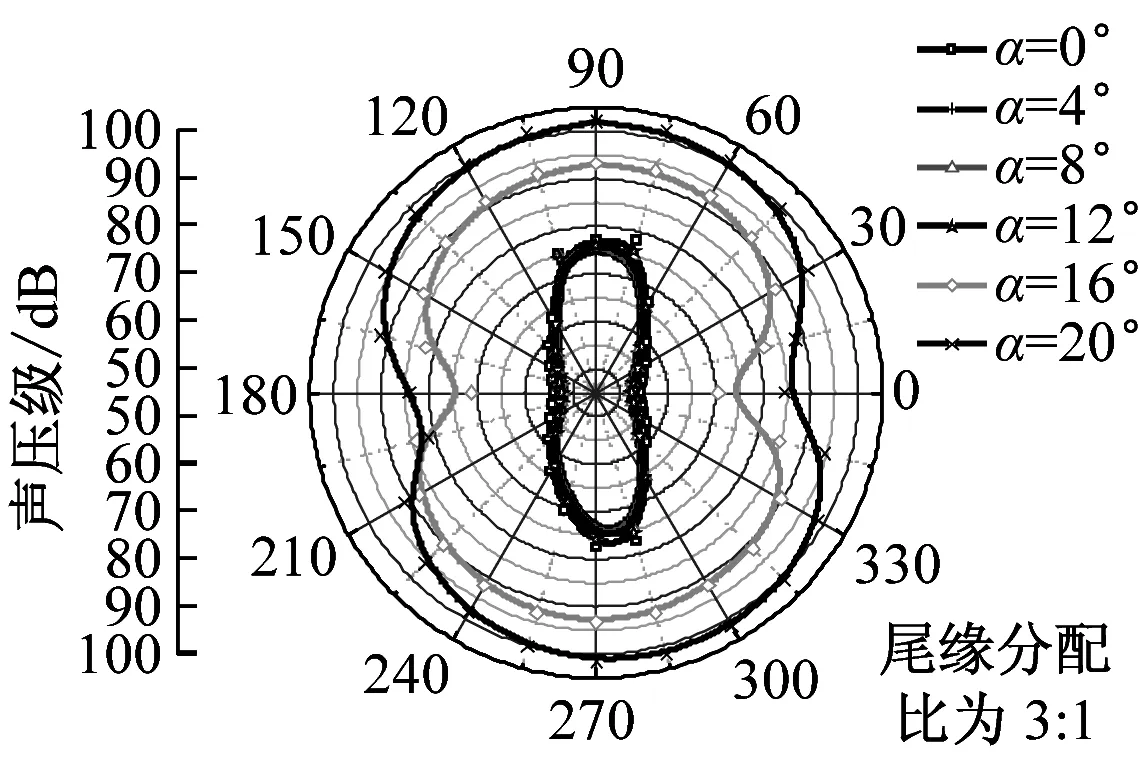
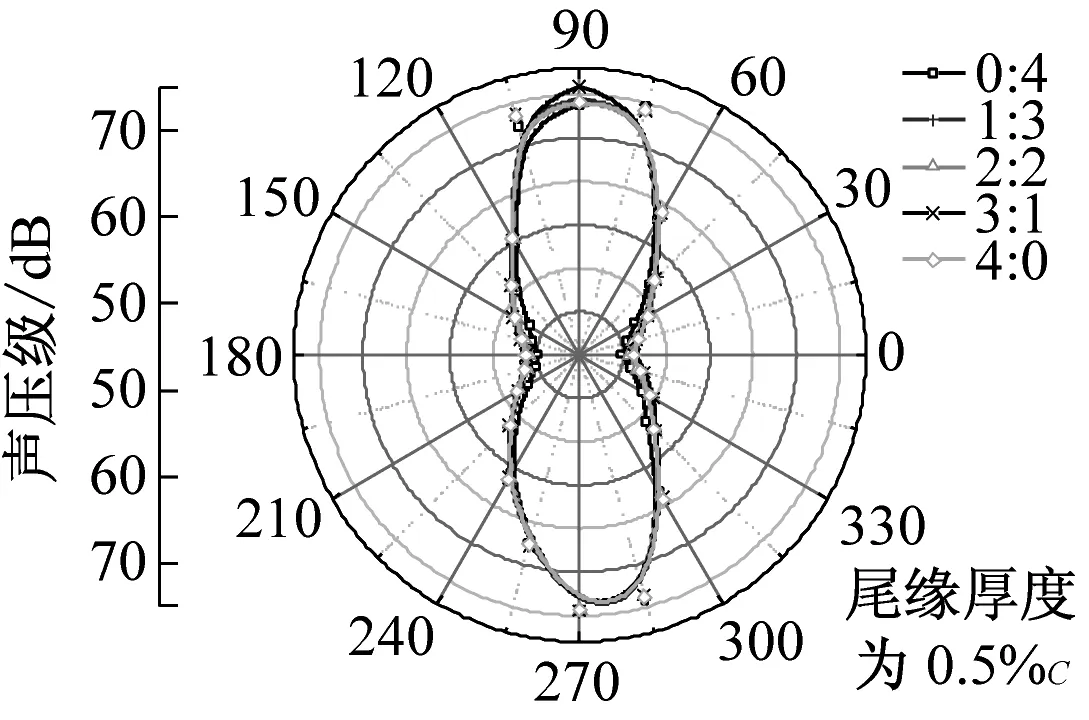
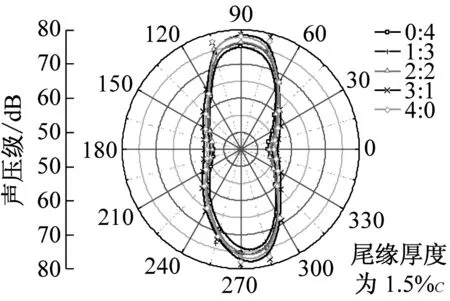
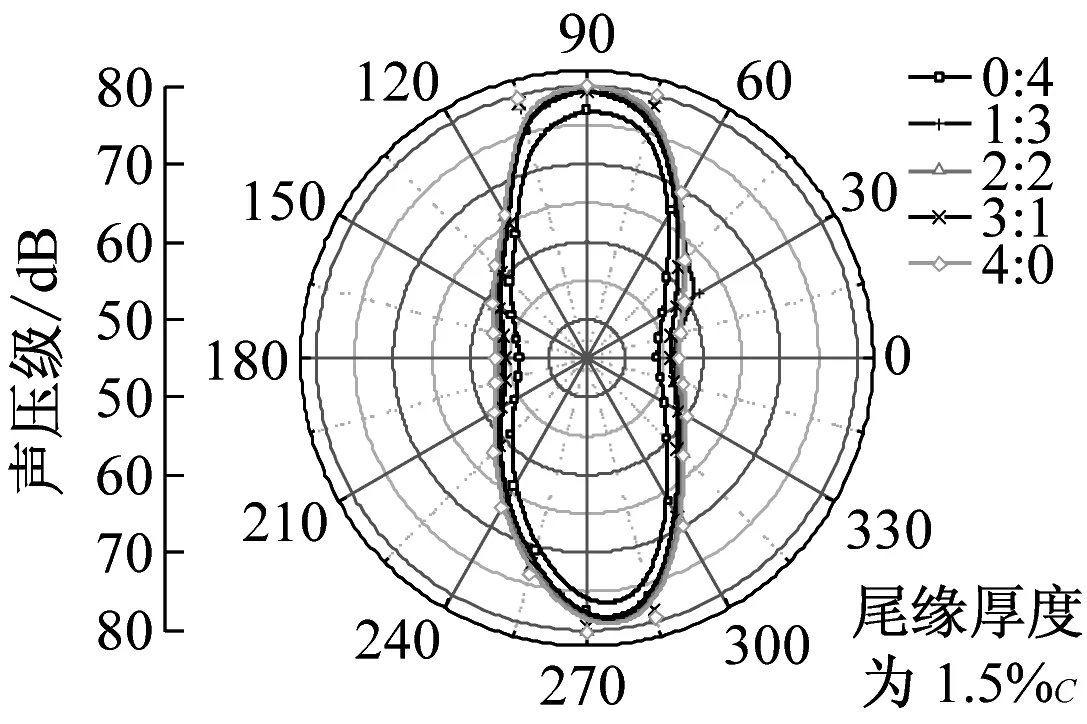
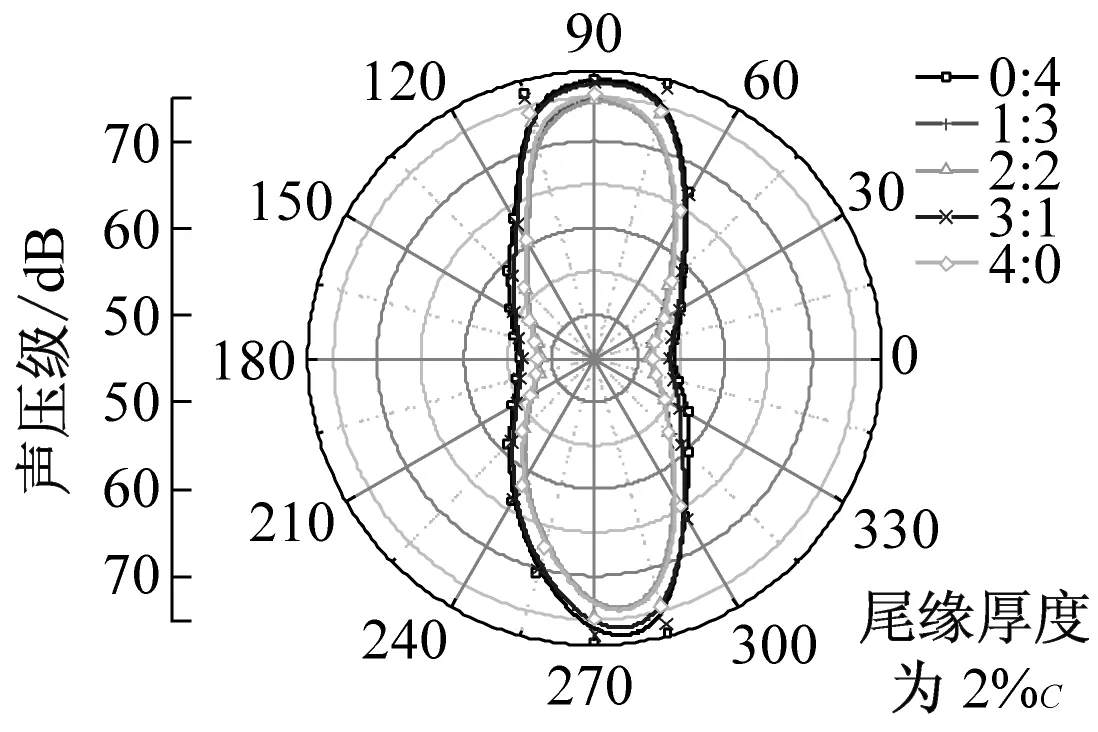
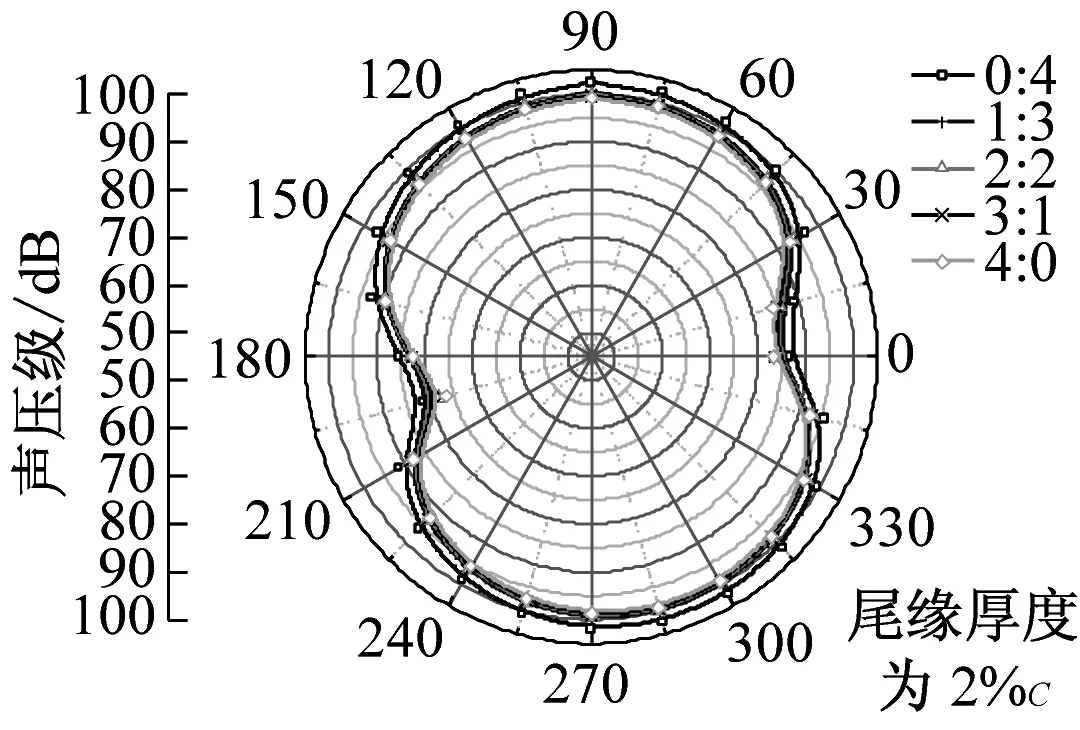
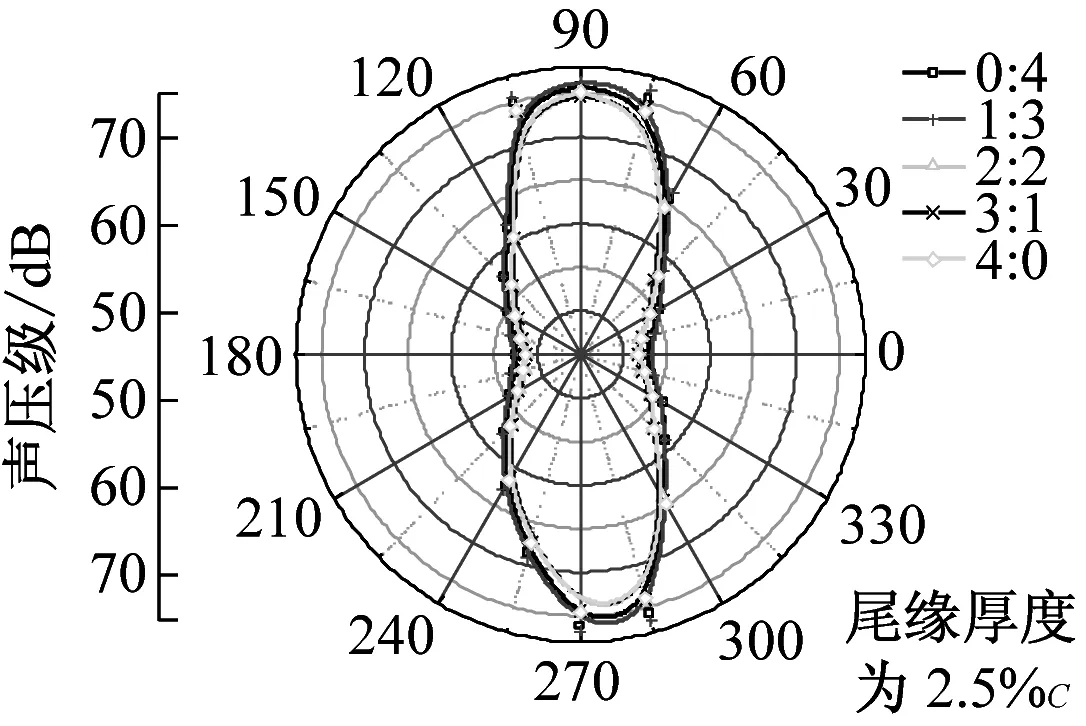
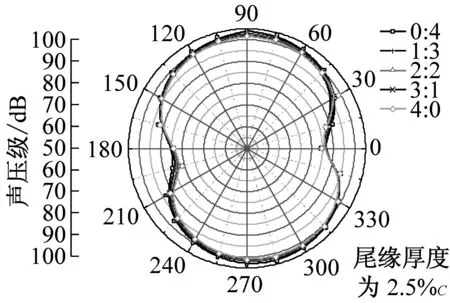
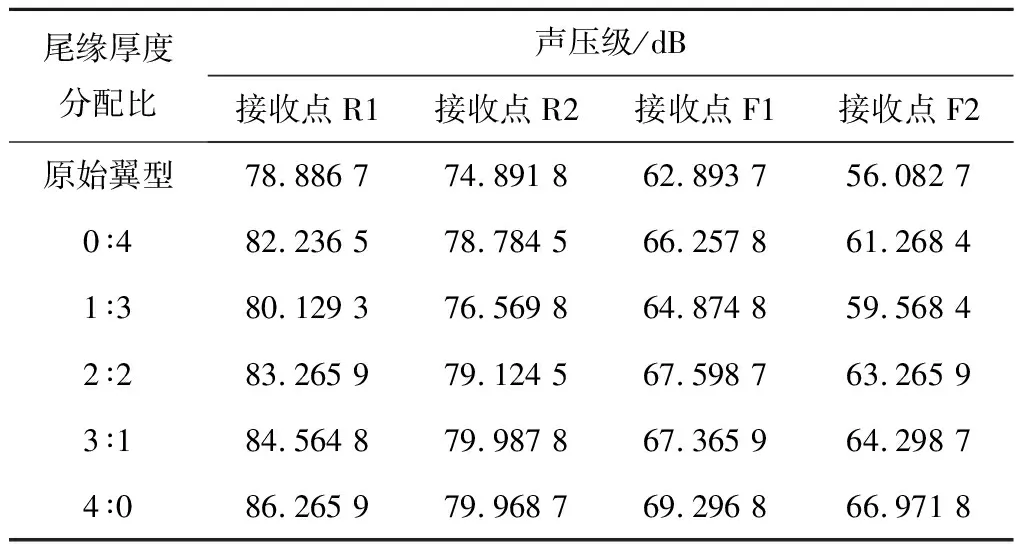
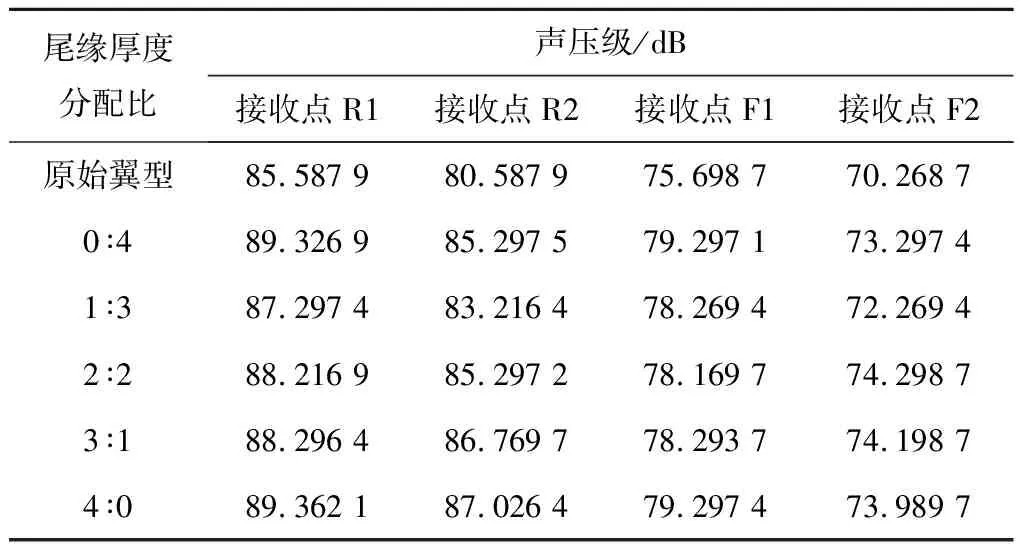
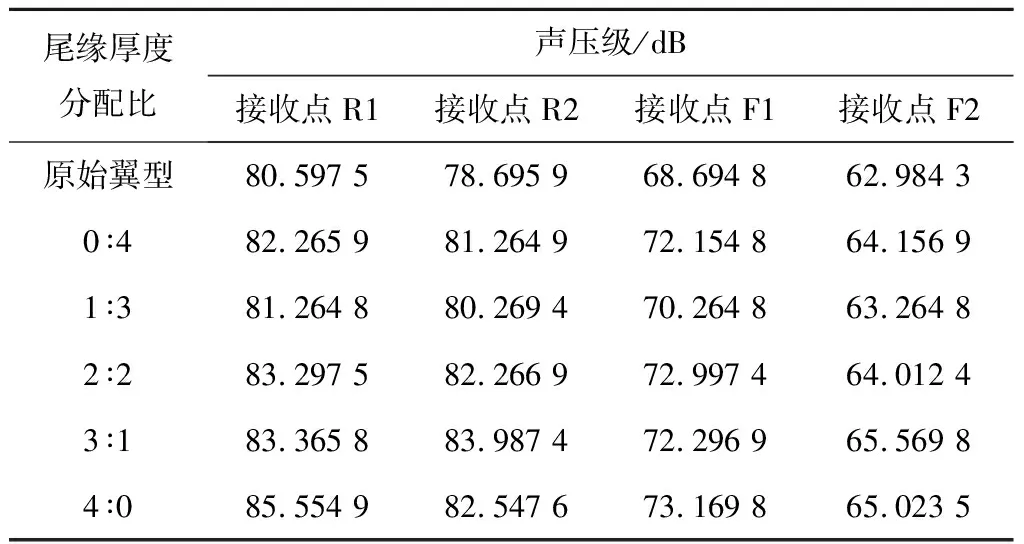
在dw Williams等[20]在Curle方程的基础上引入赫维赛德Heaviside广义函数,推导出FW-H声波波动方程。 Heaviside广义函数为: (6) f(x,t)=0时为控制面方程。引入Heaviside广义函数的流动参量,推导出FW-H方程: (7) 利用Xfoil和Matlab软件,以非对称翼型S809[21]作为原始翼型,在翼型最大厚度0.2 m处进行翼型尾缘改型处理。在原始翼型的基础上,保证最初翼型的弯度和弦长c、最大相对厚度b及其在翼型的位置点不变,最大厚度位置到尾缘点之间的不同表面光滑曲线对翼型气动性能的影响很小[22]。将翼型尾缘改为0.5%c、1%c、1.5%c、2%c和2.5%c这5种不同的尾缘厚度,在每个厚度下按尾缘厚度分配比i/n(0∶4、1∶3、2∶2、3∶1和4∶0)分为5种钝尾缘翼型。基于样条函数参数化、尾缘厚度和尾缘厚度分配比对原始翼型进行改型,如图1所示。 图1 翼型改型示意图 (8) 式中:h为尾缘厚度,m;c为弦长,m;(xk,b,yk,b)为翼型面上最大厚度位置的坐标,i=0,1,…,n。 当尾缘厚度分别为0.5%c、1%c、1.5%c、2%c和2.5%c时,尾缘厚度分配比分别取0∶4、1∶3、2∶2、3∶1和4∶0,翼型S809钝尾缘取为最大厚度点后的改型型线,如图2所示。 (a) i/n=0∶4(b) i/n=1∶3(c) i/n=2∶2 (d) i/n=3∶1(e) i/n=4∶0 图2 改型翼型 Fig.2 Modified airfoils 采用S809翼型,其弦长c=1 m,计算域由上游来流区和下游尾迹区组成,如图3所示。其中,上游来流区为15c半圆形区域,下游尾流区为20c×30c的长方形区域。为分析翼型噪声,在翼型周围设置4个检测点,分别位于尾缘上部和后部,如图4所示。其中,R1和R2分别位于翼型尾缘上方5c和10c位置处,F1和F2分别位于尾缘后部2c和5c位置处。以前缘点为圆心、半径为5c的圆周上间隔15°设置25个监测点,得到远场声压级的指向性特征。 图3 流场计算域示意图 图4 声场监测点布置 图5为计算域网格分布。在翼型前缘、尾缘、压力面和吸力面进行了网格局部加密处理,如图5(b)所示。翼型表面第1层网格尺寸为1.23×10-5m,网格增长率为1.05,计算域网格总数为58 696。尾缘网格质量良好,将外边界设置为压力远场,翼型为无滑移壁面。 (a) 全局网格(b) 局部网格 图5 计算域网格划分 Fig.5 Meshing of the calculation domain 设置边界条件:工质为理想气体,采用速度进口,v=30 m/s,基于弦长的雷诺数为2×106;采用压力出口,定义出口压力相对大气压力为0 Pa;采用二阶迎风的离散格式进行求解,设置二阶隐式时间推进法来提高计算精度。在计算域内利用Transition SST四方程湍流模型进行稳态计算,以初始化流场,再进行非稳态计算,采用DES模型进行非稳态计算,DES模型中近壁面的附面层采用RANS方法中的SST-ω模型。源相关参考长度均取5倍弦长,基于宽频带噪声的特性,当翼型升阻力系数达到稳定时开始采集流场数据和声源数据。采用SIMPLEC算法,时间步长为5×10-5s,共计算8 000步,结束时间为0.2 s。 3.1.1 有效性验证 为验证所选模型的有效性,对翼型的气动性能进行计算,并将计算值与实验值进行对比,实验数据来自文献[23]。图6给出翼型升力系数CL和阻力系数CD的计算值与实验值。由图6可知,攻角α小于12°时,在附着流域升力系数计算值与实验值非常吻合,在失速域升力系数计算值大于实验值,最大偏差均不超过4%;在附着流域阻力系数计算值与实验值吻合较好,在失速域阻力系数计算值略小于实验值。综上,升力系数和阻力系数的计算值与实验值基本吻合,说明建立的模型、网格质量和边界条件合理,计算结果准确有效。 3.1.2 尾缘改型对翼型气动性能的影响 图7给出改型翼型在不同攻角和尾缘厚度下的 图6 升力系数和阻力系数计算值与实验值的对比 Fig.6 Comparison of lift coefficient and drag coefficient between calculated results and experimental data (a) 尾缘厚度为0.5%c(b) 尾缘厚度为1%c (c) 尾缘厚度为1.5%c(d) 尾缘厚度为2%c (e) 尾缘厚度为2.5%c Fig.7 Lift and drag coefficient of modified airfoil with different trailing edge thicknesses 升力系数和阻力系数。由图7可知,在较小尾缘厚度(0.5%c和1%c)下,攻角小于8°时改型翼型的升力系数与原始翼型相差不大;攻角大于8°时,改型翼型的升力系数大于原始翼型。在较大尾缘厚度(1.5%c、2%c和2.5%c)下,攻角小于8°时改型翼型的升力系数与原始翼型相差较大;攻角大于8°时,改型翼型的升力系数随尾缘厚度的增大而增大,且均大于原始翼型。攻角小于8°时,各翼型阻力系数随尾缘厚度的增大而增大,且均大于原始翼型;攻角大于8°时,各翼型阻力系数反而略有减小,且均小于原始翼型,尾缘厚度相同时,在0°~ 8°攻角范围内升力系数随尾缘厚度分配比的增大呈递减趋势,且尾缘厚度越大,递减趋势越明显。攻角达到16°后,改型翼型和原始翼型的升力系数随攻角的增大均呈减小趋势。相比原始翼型和其他改型翼型,尾缘厚度分配比为0∶4时,大攻角下改型翼型的升力系数减幅较大。 图8给出了原始翼型和改型翼型升阻比的变化趋势。由图8可知,随着尾缘厚度的增大,各升阻比曲线均呈先升高后降低的趋势。尾缘厚度小于2%c时,改型翼型的升阻比大于原始翼型;尾缘厚度大于2%c时,改型翼型的升阻比逐渐小于原始翼型。这表明尾缘厚度过大会影响翼型的气动性能。 (a) 尾缘厚度为0.5%c(b) 尾缘厚度为1%c (c) 尾缘厚度为1.5%c(d) 尾缘厚度为2%c (e) 尾缘厚度为2.5%c 升阻比随尾缘厚度分配比的增大呈先增大后减小的趋势,且当尾缘厚度超过2%c后,趋势更明显。当尾缘厚度为1.5%c时,其升阻比大于其他尾缘厚度下改型翼型的升阻比,其中尾缘厚度分配比为1∶3的非对称改型翼型的升阻比最大。 选取不同尾缘厚度(0.5%c、1.5%c和2.5%c)计算不同攻角下的噪声,如图9所示。根据翼型自噪声理论,翼型自噪声为偶极子[24]。由图9可知,在不同攻角和尾缘厚度分配比下翼型噪声明显呈偶极子形状,与理论相符。噪声的指向性分布基本沿上下轴对称分布,但沿左右轴为不对称分布,且翼型下游噪声大于前缘噪声,这是因为钝尾缘翼型噪声主要集中在尾缘处,与翼型尾缘脱落涡及分离漩涡有关。 在小攻角范围内声压级沿上下轴基本对称分布,但在16°~20°攻角下不沿上下轴对称,此时声压级在圆周方向上的分布偏转了一定角度,其规律不随尾缘厚度的变化而变化。在大攻角下随着攻角的增大,声压级变化不大。由图9(a)可知,当尾缘厚度为0.5%c时,在较小攻角(0°、4°和8°)下翼型声压级大小相近,在较大攻角(12°、16°和20°)下声压级强度随着攻角的增大呈递增趋势,且其偶极子特性明显。由图9(b)和图9(c)可知,当尾缘厚度为1.5%c和2.5%c时,在各攻角(0°、4°、8°和12°)下翼型声压级大小相近,这说明在钝尾缘翼型噪声中尾缘脱落涡的噪声占主导地位。当尾缘厚度分配比一定时,翼型声压级随尾缘厚度的增大而增大。对于同一翼型,在小攻角下翼型处于流动附着区,翼型周围噪声声压级无明显变化,之后攻角逐渐增大至失速边缘,流体流动分离加剧,翼型尾缘在尾缘脱落的涡街和分离漩涡的双重作用下,翼型周围噪声声压级随着攻角的增大而增大,且随着尾缘相对厚度的增加而逐渐增大。 图10为翼型在不同尾缘厚度情况下噪声指向性分布规律,分别取4°、12°和20°攻角对不同尾缘厚度的翼型噪声指向性进行分析。从图10可知,翼型噪声声压级随着攻角的增加而增大,同时在大攻角状态下偶极子特性更加明显。当尾缘厚度增加时各个点的声压级呈递增趋势,与攻角大小无关,与翼型自噪声理论相符;尾缘厚度越大,噪声的声压级越大。由图10(a)可知,在小攻角情况下,随着尾缘厚度的增加,翼型噪声的声压级变化较不明显,且在不同的尾缘分配比下其变化亦不明显。由图10(b)可知,在失速区情况下,翼型噪声声压级的大小与不同尾缘分配比的关系不明显,由于翼型吸力面近尾缘处出现明显流动分离,导致流动状态不稳定。由图10(c)可知,在大攻角下,翼型噪声声压级分布符合偶极子特性,且当吸力面越厚时声压级越小。尾缘厚度越大其沿左右轴的偏转越大。当尾缘厚度分配比为4∶0时,各个尾缘厚度下其噪声声压级最小。 (a) 尾缘厚度0.5%c (b) 尾缘厚度1.5%c (c) 尾缘厚度2.5%c 在流场中设置多个观测点,以翼型前缘点为原点,弦长方向为x轴,垂直弦长方向为y轴,在流场中取4个观测点,分别为R1(1,5)、R2(1,10)、F1(2,0)和F2(5,0)。其中,R1和R2点主要观测翼型后缘上方的气动噪声,F1和F2点主要观测翼型尾流中的气动噪声。为对比钝尾缘对气动噪声的影响,仅在0°攻角下选取钝尾缘厚度为1.5%c的改型翼型与原始翼型进行对比。 由图11(a)和图11(b)可知,在低频区原始翼型或改型翼型的声压级分布存在峰值,明显是低频特性。钝尾缘改型翼型的声压级明显大于原始翼型,这是因为钝尾缘尾缘厚度较大,尾缘厚度分配比对涡街强度影响较小,尾缘噪声始终在噪声源中占比较重,声压级分布呈低频特性,频谱图在低频处均呈先上升后下降的趋势,在高频处趋于小幅震荡状态。由图11(c)和图11(d)可知,2处的接收点处呈较明显的低频特性,且分布初显宽频特性,钝尾缘翼型声压级大于原始翼型,不同尾缘厚度分配比仍有一定的差异。小攻角时,同时存在湍流边界层尾缘噪声和层流边界层脱落涡噪声等,两者相互作用,使得翼型不同方向上声压级分布规律有所差别。 (a) 攻角为4° (b) 攻角为12° (c) 攻角为20° (a) 接收点R1(b) 接收点R2(c) 接收点F1(d) 接收点F2 图11 声压级分布 Fig.11 Distribution of sound pressure level 随着尾缘厚度的增大,离散噪声增强,在高频段声压级也逐渐增大。攻角不变时,漩涡主要是由翼型尾缘厚度引起的,尾缘处的漩涡结构会伴随着更复杂的分离流动,这是引起尾缘噪声的主要原因。当尾缘厚度分配比为1∶3时,R1点低频段的峰值为80.129 3 dB,均小于其他尾缘厚度分配比下的峰值,大于原始翼型下的峰值(78.866 7 dB)。在F2点处尾缘厚度分配比为1∶3时低频段的峰值也较小。R2和F1点情况相同。 表1给出了在0°攻角下,尾缘厚度为1.5%c的钝尾缘翼型各接收点的声压级。由表1可知,各钝尾缘翼型噪声均大于原始翼型。在尾缘上方,气动噪声随吸力面厚度的增大而增大,与其他尾缘厚度分配比相比,尾缘厚度分配比为1∶3时声压级较小。接收点F1点和F2点处,随着尾缘厚度分配比的增大,气动噪声也增大。 表1 0°攻角下钝尾缘翼型各观测点声压级 由表2和表3可知,在各攻角下钝尾缘翼型声压级始终大于原始翼型,与翼型自噪声理论相符。随着攻角的增大,翼型平均总声压级呈增大趋势。由于F1和F2点处于下翼面远尾流区,涡脱落不再集中于翼型的尾缘,导致流场状况复杂。 表2 8°攻角下钝尾缘翼型各观测点声压级 表3 16°攻角下钝尾缘翼型各观测点声压级 (1) 通过样条函数参数化处理改型后的钝尾缘翼型,与原始翼型相比,在一定尾缘厚度及其尾缘厚度分配比范围内,气动性能得到明显改善。 (2) 通过验证原始翼型的气动性能和声压频谱,证明以分离涡模拟方法和声学类比方程建立的噪声预测方法的可靠性。 (3) 钝尾缘翼型会导致气动噪声增大,但尾缘厚度为1.5%c、尾缘厚度分配比为1∶3的钝尾缘翼型的气动噪声增幅较小。1.2 FW-H声波波动方程

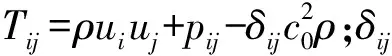
2 数值计算
2.1 非对称钝尾缘翼型改型
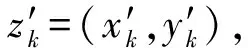
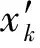

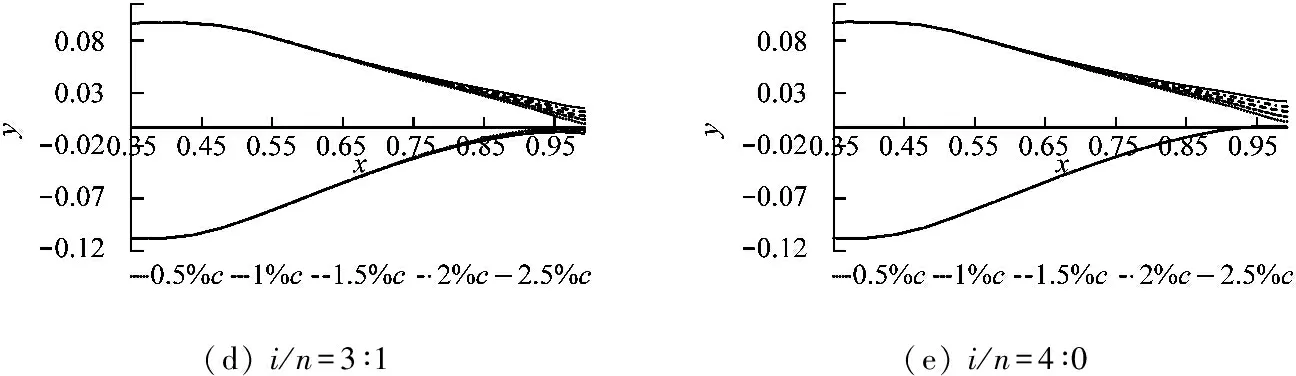
2.2 计算设置及监测点分布


3 结果与分析
3.1 气动性能
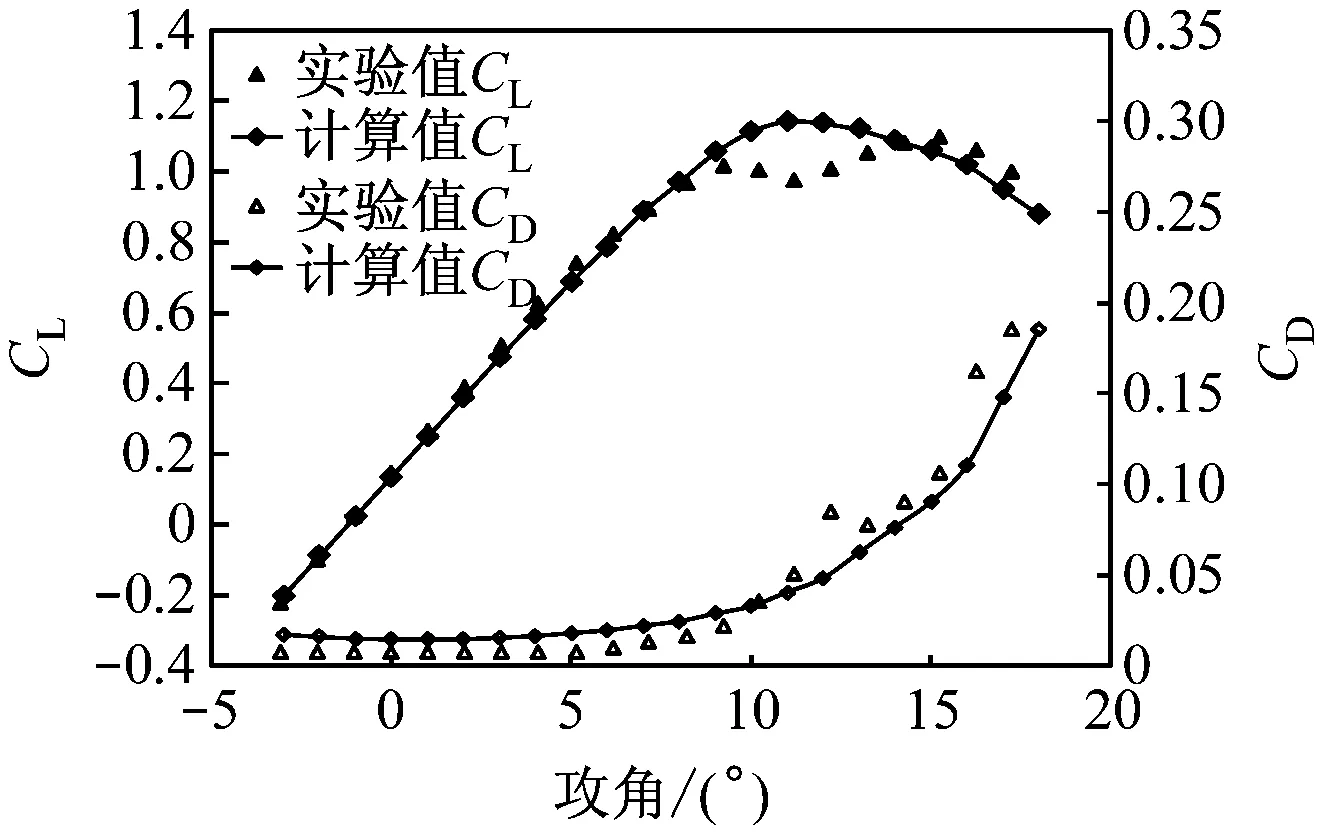
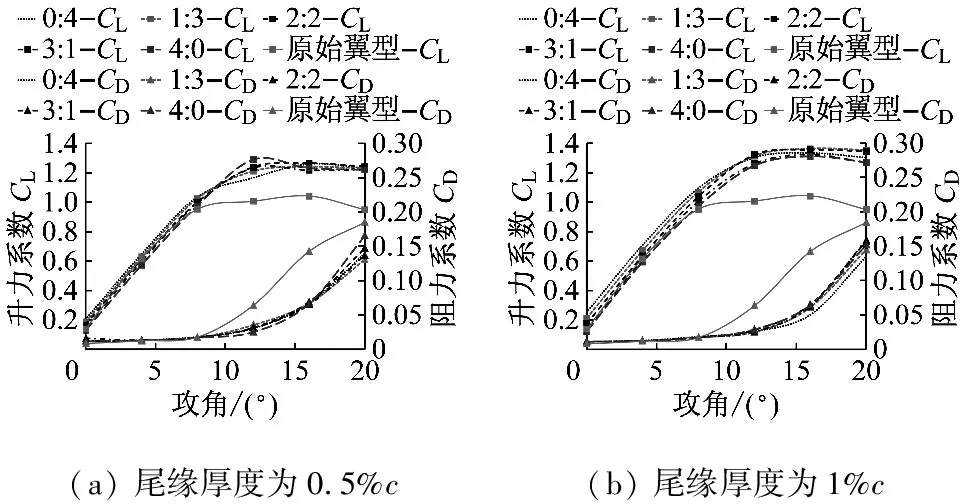
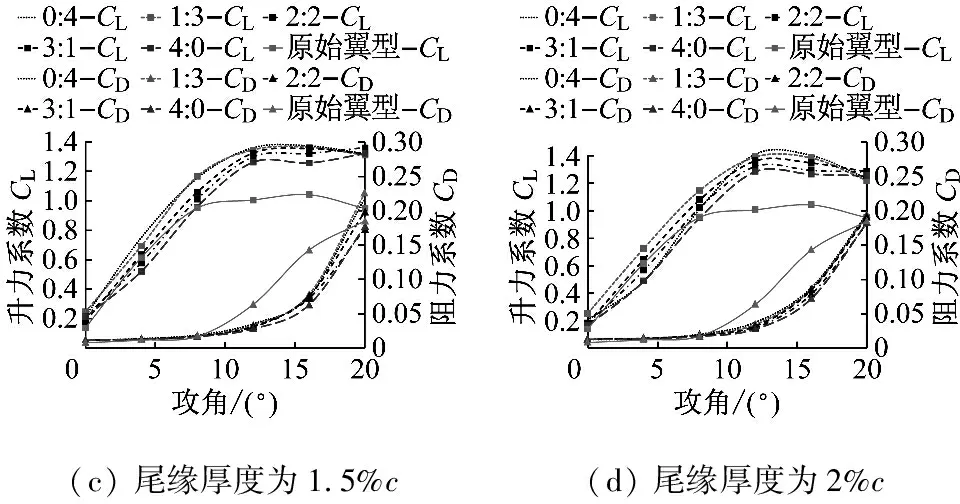
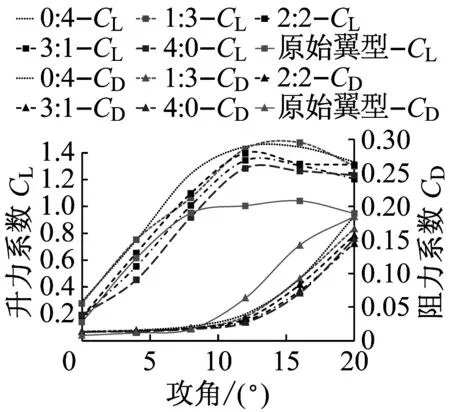
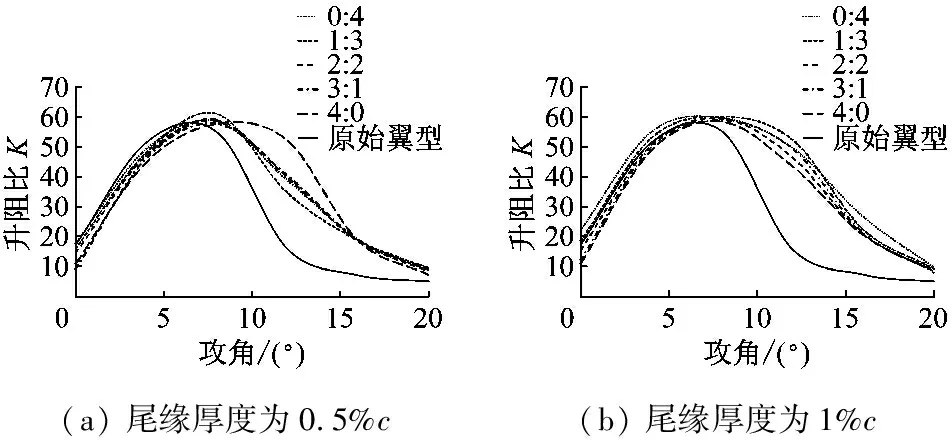
3.2 噪声特性分析












4 结 论

