核电安全壳中分离式热管蒸发段流动沸腾模拟
孙海彤, 虞 斌, 涂善东
(1.南京工业大学 机械与动力工程学院,南京 211800;2.华东理工大学 机械与动力工程学院,上海 200237)
2011年福岛核电事故再次给核电安全敲响了警钟,对提高核电站安全壳固有安全性的研究引发了更为广泛的关注。在正常工作情况下,安全壳中压力接近大气压,温度低于50 ℃。然而,当冷却剂丧失事故(LOCA)或者主蒸汽管道破裂(MSLB)等事故发生后,反应堆回路中高温高压水泄漏进入安全壳中,高温高压水在低压环境中迅速蒸发并产生大量水蒸气,促使安全壳中压力和温度迅速升高,严重威胁安全壳的安全性和完整性[1-2]。分离式热管具有无需电力驱动和换热效率高的优点,采用外部水池作为热阱,可以非能动地导出安全壳中的余热,保障事故发生时安全壳的完整性。许多学者对传统的分离式热管蒸发段进行了实验和模拟研究[3-5]。考虑到安全壳的尺寸较大,拟采用大型的分离式热管来冷却安全壳。大尺度分离式热管的流体动力学性能和热性能与传统的热管有很大区别,不一定适用于传统热管实验得到的经验公式。因此,笔者采用计算流体力学(CFD)模型来模拟大型热管的基础流动特性,为核电安全壳分离式热管非能动冷却系统的开发提供参考。
1 系统简介
核电安全壳分离式热管非能动冷却系统如图1所示,分离式热管蒸发段布置在安全壳内部,冷凝段布置在安全壳外的冷却水池中,当安全壳中热量超过给定值时,分离式热管将开始工作,并源源不断地将安全壳中的热量带到安全壳外的冷却水池中。整个过程不需要外力驱动,属于完全的非能动冷却。主要设计参数总结在表1中,蒸发段采用外径89 mm、壁厚4.5 mm、长6 m的不锈钢管1 680根,分成12等份,每份由2个70根不锈钢管组成的蒸发器组成,均匀分布在安全壳中。冷凝段采用外径89 mm、壁厚4.5 mm、长4 m的不锈钢管2 160根,分为12等份,每份由2个90根不锈钢管组成的蒸发器组成,均匀分布在安全壳中。
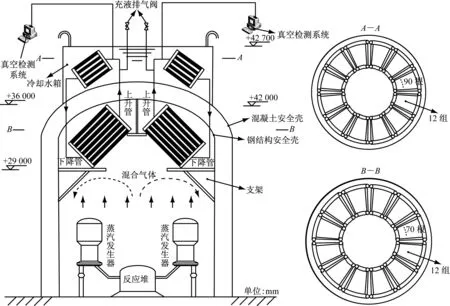
图1 采用分离式热管的安全壳示意图
2 数值模型及计算方法
2.1 数值模型
热管蒸发段采用垂直或倾斜布置,模型长度为6 m,内径为80 mm。如图2所示,冷凝段产生的冷凝水从蒸发段的底部进入蒸发段,通过壁面加热变成蒸汽后从蒸发段的顶部流出到绝热段。冷凝水流量和出口压力均为定值。
2.2 控制方程
所研究的分离式热管蒸发段的气液两相流流动沸腾是多相流动问题。在 Fluent 软件中,基于经典的连续介质力学方法有欧拉-拉格朗日方法和欧拉-欧拉方法。其中,欧拉-欧拉方法更常用,流体体积函数(VOF)模型、Mixture模型和Eulerian模型均属于欧拉-欧拉类型,其特点是不同的相被视为相互连通的连续介质。由于相与相之间的体积是相互隔离的,彼此都不能被占有,因此提出了相体积率的概念。它是时间和空间的连续函数,各相的体积率之和为1[6]。在此次模拟中,气液两相的蒸发与冷凝模拟是重点。它具有分层、自由面流动和泡状流的综合特征,适合采用VOF模型模拟流动沸腾现象[7-10]。

表1 热管非能动冷却系统的主要参数

图2 蒸发段示意图
因为管子中的流动沸腾只有两相参与,VOF的控制方程如下:
连续性方程:
(1)

(2)
动量方程:

(3)
能量方程:
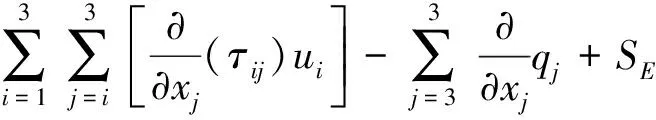
(4)
式中:SM为质量源相,kg/m3;SF为动量源相,N/m3;SE为能量源相,W/m3;ui和uj分别为xi轴和xj轴的速度分量,m/s;δij为克罗内克函数;E为流体微团的总能,J/kg;τij为黏性应力分量,Pa;qj为j方向的导热热流密度,J/(m2·s);ρ为流体的密度,kg/m3;ρl为饱和液体密度,kg/m3;ρv为饱和蒸汽密度,kg/m3;μ为动力黏度,Pa·s;ρ、μ的值取决于各项的体积分数φ。
ρ、μ的计算公式为:
ρ=φ1ρ1+φ2ρ2
(5)
μ=φ1μ1+φ2μ2
(6)
采用连续表面力模型(CSF)计算表面张力[11]:
(7)
式中:σ为气液相间的表面张力;k为界面的曲率。
(8)
对于蒸发冷凝过程,Lee提出的模型应用最为广泛[12-13],笔者采用Lee提出的方程计算源相,如表2所示[14],表中β为蒸发冷凝系数,取β=0.1[12-14];Tl为液相温度,K;Tv为气相温度,K;Tsat为饱和温度,K;ΔH为蒸发焓,J/kg。

表2 质量及能量转移源项
2.3 模拟计算方法
使用Fluent软件对热管蒸发段内沸腾传热传质流动过程进行数值模拟。管壁采用第三类边界条件来加热工作流体。采用VOF模型模拟管内的流动变化现象和热性能,采用可实现k-ε湍流模型模拟两相流流动[6],压力差值采用body force weight格式,采用二维非稳态求解器,控制方程的离散采用有限单元体积法,采用SIMPLE速度-压力耦合,动量和能量方程采用二阶迎风算法,湍动能分量和耗散率采用一阶迎风算法,采用连续表面力模型,工质相变采用蒸发冷凝模型。
3 计算验证
在现有文献中,有关大直径管道中工质流动沸腾的实验研究很少。笔者通过将模拟结果与以往研究结果进行比较,验证了上述数值模型的合理性。对内径为80 mm的换热管模型进行了网格独立性验证。在模拟中,进行足够长时间的计算,以确保蒸发管达到热平衡状态。另外,为了进一步验证数值模型的合理性,对模拟结果与实验所得的Rohsenow经验关联式的计算结果进行比较。
3.1 网格独立性验证
为了验证数值计算的准确性,在质量流量90 kg/h、对流传热系数600 W/(m2·K)、饱和温度373 K和外部流体温度395 K的工况下,选取4组不同的网格对数值模型进行模拟,计算不同网格数下分离式热管的努塞尔数,结果如表3所示。由表3可知,对于7 500、14 000、30 000和120 000个网格的模拟,误差均低于4%。因此,上述数值模型可以在单根热管中模拟流动沸腾过程的一些基本机制。考虑到计算时间和计算准确性,使用14 000个网格的模拟结果。
表3不同网格数下热管传热系数的变化
Tab.3Variationofheatpipeheattransfercoefficientunderdifferentgridnumbers
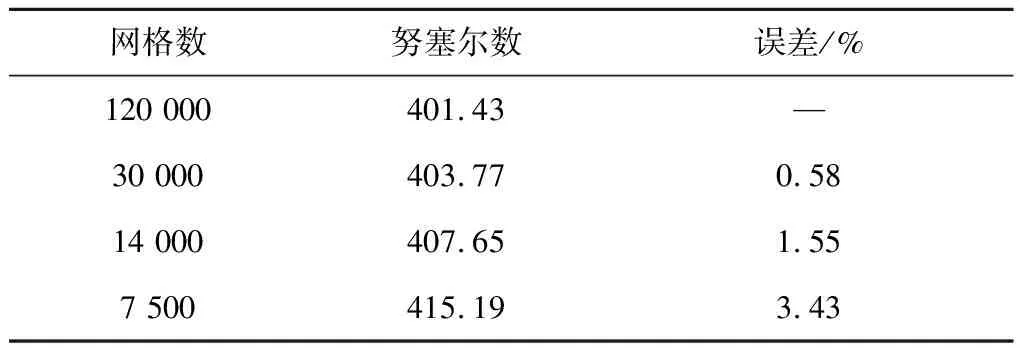
网格数努塞尔数误差/%120 000401.43—30 000403.770.5814 000407.65 1.557 500415.193.43
3.2 模型验证
在分离式热管循环回路中,管内工质的流动是由液相之间的位压差和汽液相之间的密度差决定的,而且汽相与液相的流动方向一致,蒸发段中流动和沸腾传热同时进行并相互影响,因而可将分离式热管蒸发段中的传热过程归结为管内汽液两相流动沸腾传热的过程[15]。
根据以往的研究[16-17],管道中的饱和沸腾受2种主要因素控制,即核态沸腾和强制对流沸腾。Rohsenow根据实验数据整理了核态沸腾的无量纲关系式[18]:
(9)
式中:cp,l为饱和液体比热容,J/(kg·K);Δt为壁面过热度,K;r为汽化潜热,J/kg;Prl为饱和液体普朗特数;s为经验指数,对于水s=1;Cwl为经验常数,取决于加热表面和液体,本文管内介质为水,换热管材料选取不锈钢,取Cwl=0.013 0[19];q为热流密度,J/(m2·s);μl为饱和液体动力黏度,Pa·s;g为重力加速度,m/s2。
选取内径为80 mm的垂直管在质量流量90~180 kg/h、外部对流传热系数400~800 W/(m2·K)、管外流体温度385~395 K和饱和温度373 K的工况下进行数值模拟,为了保证算法的正确性,将数值模拟结果与Rohsenow无量纲关系式的计算结果进行了对比。
壁面过热度Δt由下式计算:
Δt=Twall-Tsat
(10)
热流密度q由下式计算:
q=hout(Tout-Twall)
(11)
式中:Tout为管外流体温度;Twall为壁面温度;hout为外部对流传热系数。
数值模拟结果与实验关系式计算结果的对比如图3所示。由图3可以看出,数值模拟结果与实验关系式的计算结果相差不大。已知q计算Δt时,数值模拟结果与实验关系式计算结果的偏差在20%左右,与文献中结果相符[20]。

图3 本文数值模拟结果与实验关系式计算结果的比较
4 数值模拟结果及讨论
4.1 蒸发段管内流动特性
4.1.1 垂直管两相流流型
分离式热管蒸发段换热管内,由于外部热量传入,液相被加热,壁面与液相工质接触处会产生汽泡,汽泡受热长大并上升至液面,最终破散到汽相中。汽泡作为热管中传质传热的主要媒介,其流动形态与合并过程对热管内工质的传质传热有很大影响,所以对热管中两相流的研究非常必要。
图4给出了在质量流量90 kg/h、对流传热系数600 W/(m2·K)、饱和温度373 K、外部流体温度395 K工况下,垂直布置时分离式热管蒸发段单管中汽液两相的分布情况,管道中间为汽泡,管道四周为液态水。
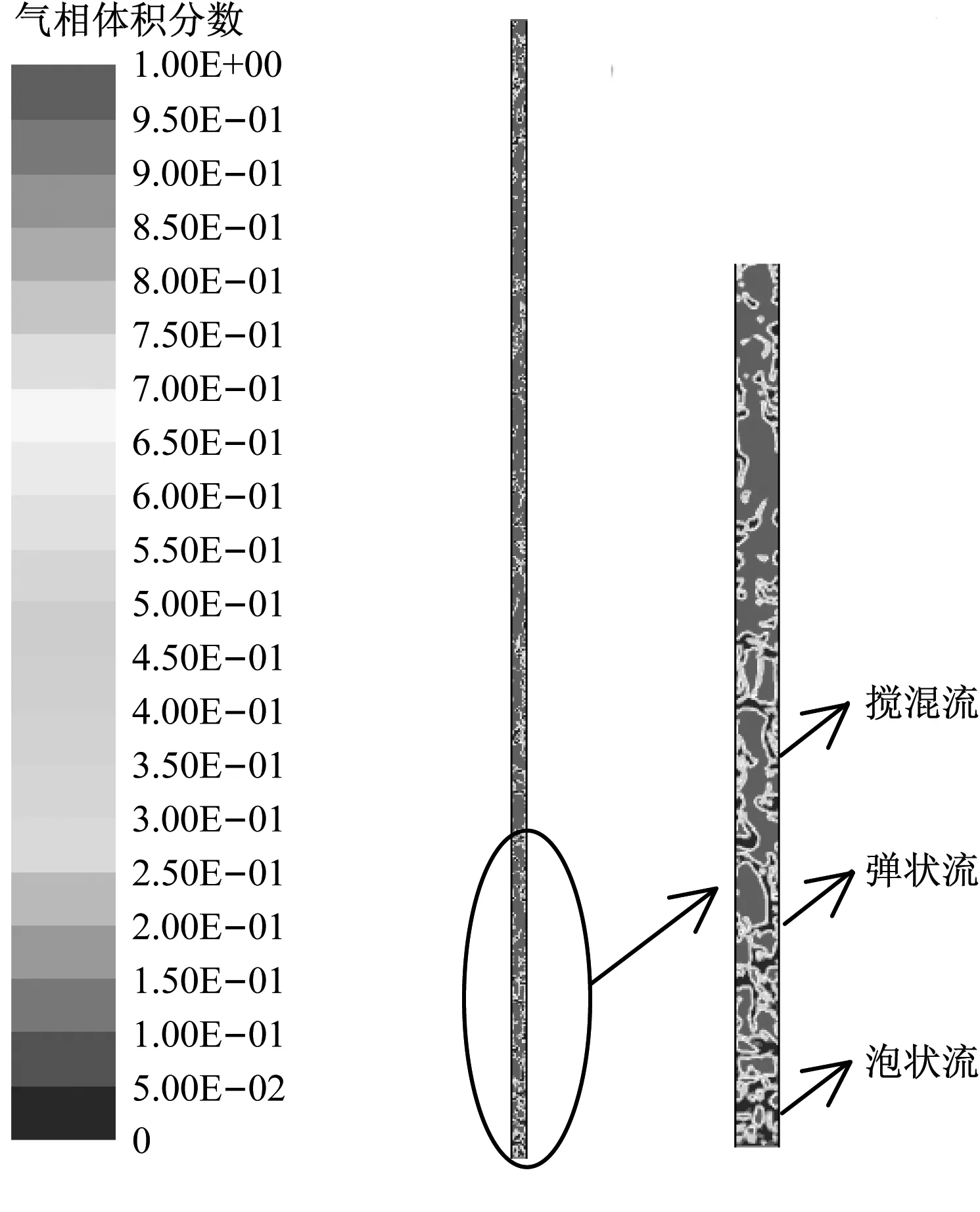
图4 垂直蒸发段管内气液相分布图
Fig.4 Distribution of vapor/liquid phase in the pipe of vertical evaporator
由图4可以看出,工质在进入管子后,被管壁加热升温,随着工质温度的升高,达到饱和温度后开始相变,壁面处开始出现体积不断长大的汽泡,形成泡状流;随着流动的进一步发展和汽相工质的增多,流型逐渐发展为弹状流和搅混流。
管道内工质的流动沸腾过程依次经历了泡状流、弹状流和搅混流。由于进口处液相体积分数为1,在蒸发段换热管的进口附近液相所占比例较大,流型为泡状流。在泡状流区域,工质由全液相转为汽液两相存在于通道中,汽泡呈较为规则的球形,在汽化点处形成、长大,并沿管壁流动。而后随着汽泡的合并和增长,流型逐渐演变为弹状流。在弹状流区域,汽泡呈子弹状,前端为椭球状,中段为平滑柱体,尾端呈扁平状,弹状气泡被小段液柱间隔开,弹状流存在范围较小。弹状流汽泡继续长大,并迅速转为搅混流。在搅混流区域,搅混流是因大气泡破裂形成的,气泡形状很不规则,且有许多小气泡掺杂在液流中,搅混流大量存在于管中。
内径为80 mm管中的两相流动行为与文献中管内汽液两相流动沸腾传热的过程吻合良好[21]。可见上述数值模型可以有效地模拟管内流体的流动方式和传热性能。
4.1.2 倾斜管两相流流型
为考察倾斜角度(下文均简称倾角)对两相流流型的影响,在质量流量90 kg/h、对流传热系数600 W/(m2·K)、饱和温度373 K、外部流体温度395 K工况下,选取50°和10°倾角布置时分离式热管蒸发段换热管中汽液两相的分布情况进行研究,结果见图5和图6。由图5和图6可以看出,受倾角影响,换热管内工质呈现出不同的流动形态。如图5所示,在换热管倾角减小到50°时,管内工质的两相流型呈现出明显的不对称特点,且在上管壁处出现间歇性的局部干涸。如图6所示,在换热管倾角减小到10°时,汽液界面呈波浪状,上管壁处不能维持湿润状态,存在较大范围的干涸区,对换热产生了不好的影响。

图5 50°倾角蒸发段管内气液相分布图
Fig.5 Distribution of vapor/liquid phase in the pipe of evaporator at an inclined angle of 50°
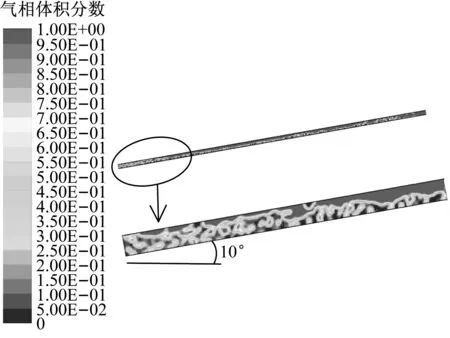
图6 10°倾角蒸发段管内气液相分布图
Fig.6 Distribution of vapor/liquid phase in the pipe of evaporator at an inclined angle of 10°
4.1.3 蒸发段管内流场
图7为垂直蒸发段管内工质流体速度分布矢量图。图中流型为弹状流和搅混流,由图7可以看出,汽相工质带动液相工质向上流动,部分液相工质回流并冲刷壁面。受气泡的影响,管内工质流体产生了不同方向的速度并形成了一个个漩涡。图8为50°倾角布置的蒸发段管内工质流体速度分布矢量图,图中流型为搅混流,与垂直蒸发段不同的是,工质呈现出沿上管壁向上流动,沿下管壁回流的现象。图9为10°倾角布置的蒸发段管内工质流体速度分布矢量图,图中流型呈波浪状,汽相工质沿管壁方向向上流动,液相工质沿管壁向下流动,汽相工质对液相工质流动状态干扰较小。

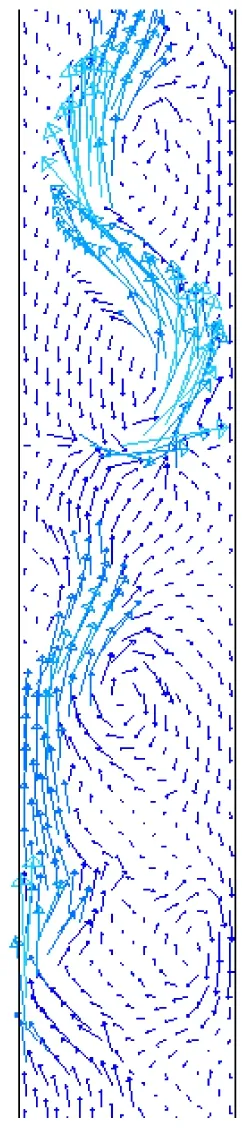

图7 垂直蒸发段管速度分布矢量图
Fig.7 Distribution of velocity vector in the pipe of vertical evaporator
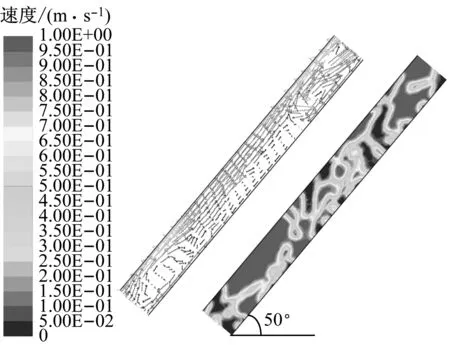
图8 50°倾角蒸发段管速度分布矢量图
Fig.8 Distribution of velocity vector in the pipe of evaporator at an inclined angle of 50°

图9 10°倾角蒸发段管速度分布矢量图
Fig.9 Distribution of velocity vector in the pipe of evaporator at an inclined angle of 10°
4.2 换热管传热的影响因素
4.2.1 倾角对传热的影响
在事故发生时安全壳中温度瞬间升高到100 °C以上,需要通过分离式热管散热来保证安全壳中的热量在设计值(148.89 °C)以下[1]。为了研究热管蒸发段的倾角对传热性能的影响,在质量流量90 kg/h、外部对流传热系数600 W/(m2·K)、外部流体温度395 K的工况下,计算了10°、20°、30°、40°、50°、60°、70°、80、90° 9种不同倾角下的传热系数。质量流量和工作温度根据分离式热管的设计来假设。由于热管安装在安全壳中,因而采用第三类边界条件。笔者采用无量纲努塞尔数来评估不同工况下的换热强度,众所周知,努塞尔数的物理意义是表示对流换热强烈程度的一个准数,又表示流体层流底层的导热阻力与对流传热阻力的比。
图10给出了不同倾角下努塞尔数的变化。由图10 可以看出,倾角在10°~90°时,努塞尔数随着倾角的增大呈增大趋势,但增大的速度逐渐减缓,在倾角为60° 时换热效果最好。考虑到分离式热管蒸发段布置在安全壳上部,蒸汽产生于安全壳下方,为了使蒸汽与换热管充分接触,达到较好的换热效果,分离式热管宜采取倾斜布置,结合本模拟,推荐分离式热管的蒸发段采取50°~80° 的倾角布置。
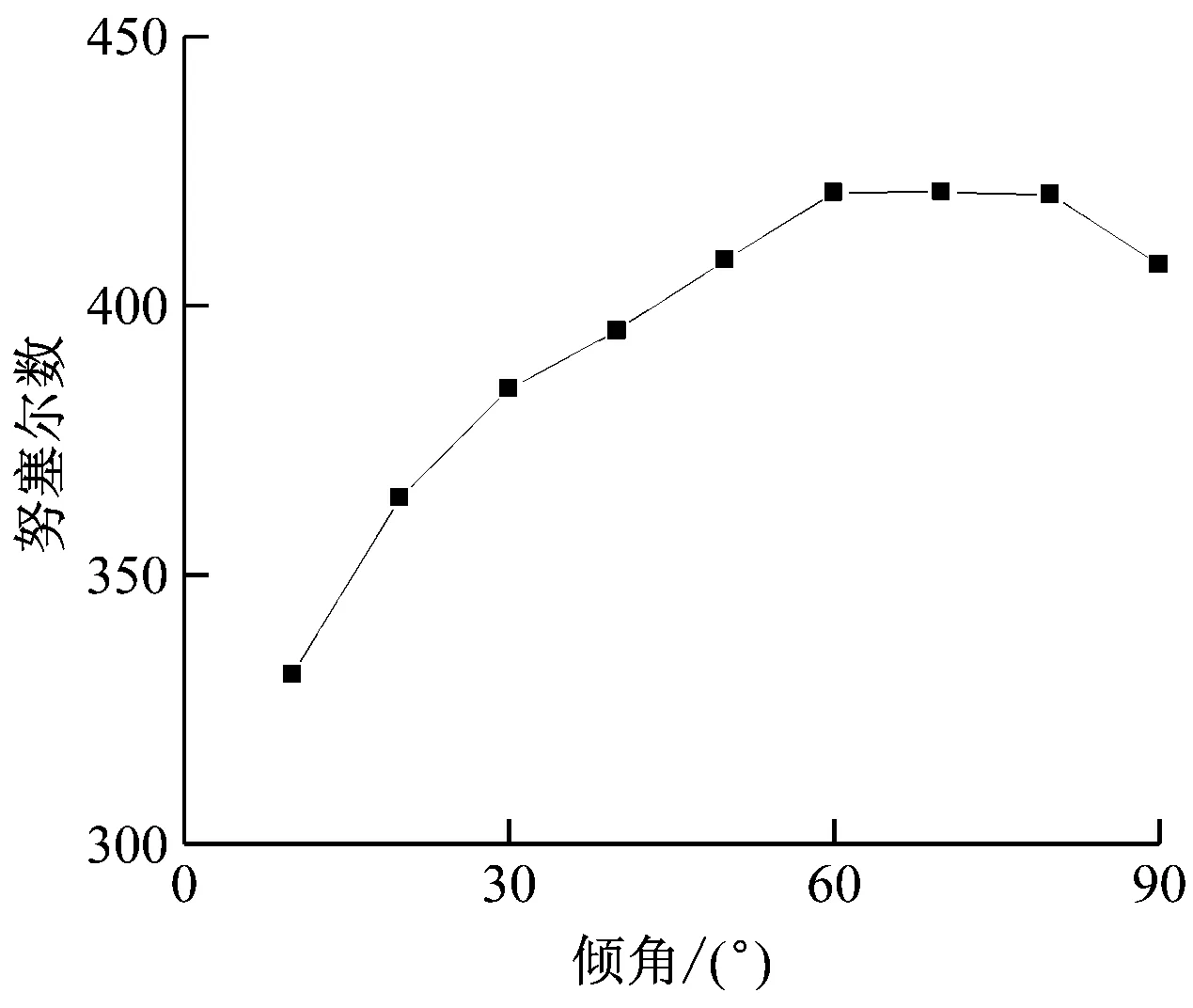
图10 不同倾角下努塞尔数的变化
4.2.2 其他因素对传热的影响
为了研究其他因素对热管蒸发段传热性能的影响,在换热管采用70°倾角布置的情况下,改变进口质量流量、外部对流传热系数及管外流体温度,选取5组不同工况进行了数值计算,其相应的工作条件见表4。质量流量和工作温度根据分离式热管的设计假设。
管道中的饱和沸腾受2种主要因素控制,即核态沸腾和强制对流沸腾。在强制对流沸腾主导的区域中,传热系数较大,有效地降低了壁面处液体的过热度,并且在壁面上不能维持成核。由于蒸发的热阻非常小,该区域的传热主要是加热壁面上液膜的对流传热,因此传热的强弱主要取决于工作流体的质量流量和蒸汽质量。在核态沸腾主导区域中,壁面处的液体过热以维持成核和汽泡生长。
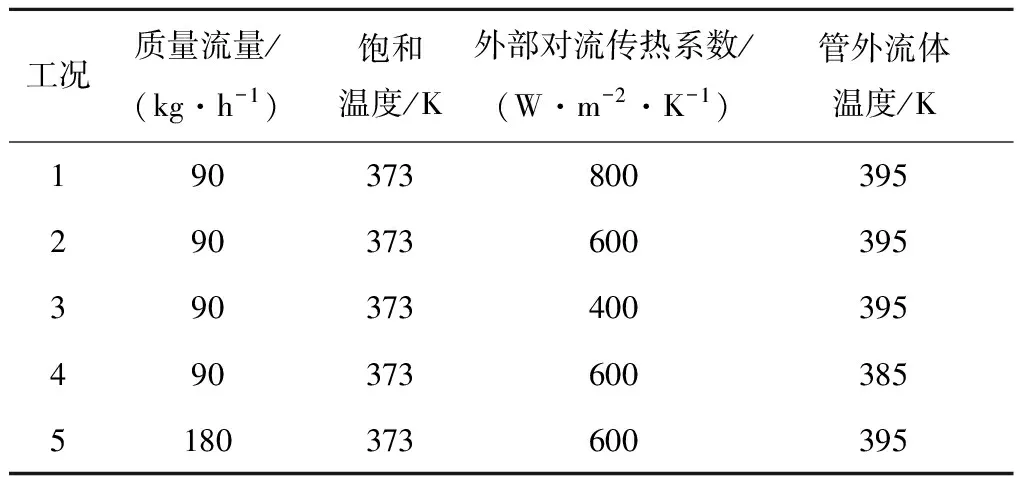
表4 蒸发段流动传热模拟参数
如图11所示,表面努塞尔数在热管启动后迅速增大,之后便趋于稳定。由工况1、工况2和工况3可以看出,较高的外部对流传热系数导致较高的表面努塞尔数。由工况2与工况4的比较可以看出,当管外流体温度由395 K下降到385 K时,表面努塞尔数明显减小,说明管外流体温度的变化对换热强度的影响较大。由工况2与工况5的比较可知,当工质质量流量从90 kg/h增加到180 kg/h时,对传热强度的影响并不大,所以说质量流量对传热的影响不大,即强制对流沸腾对传热的影响不大。
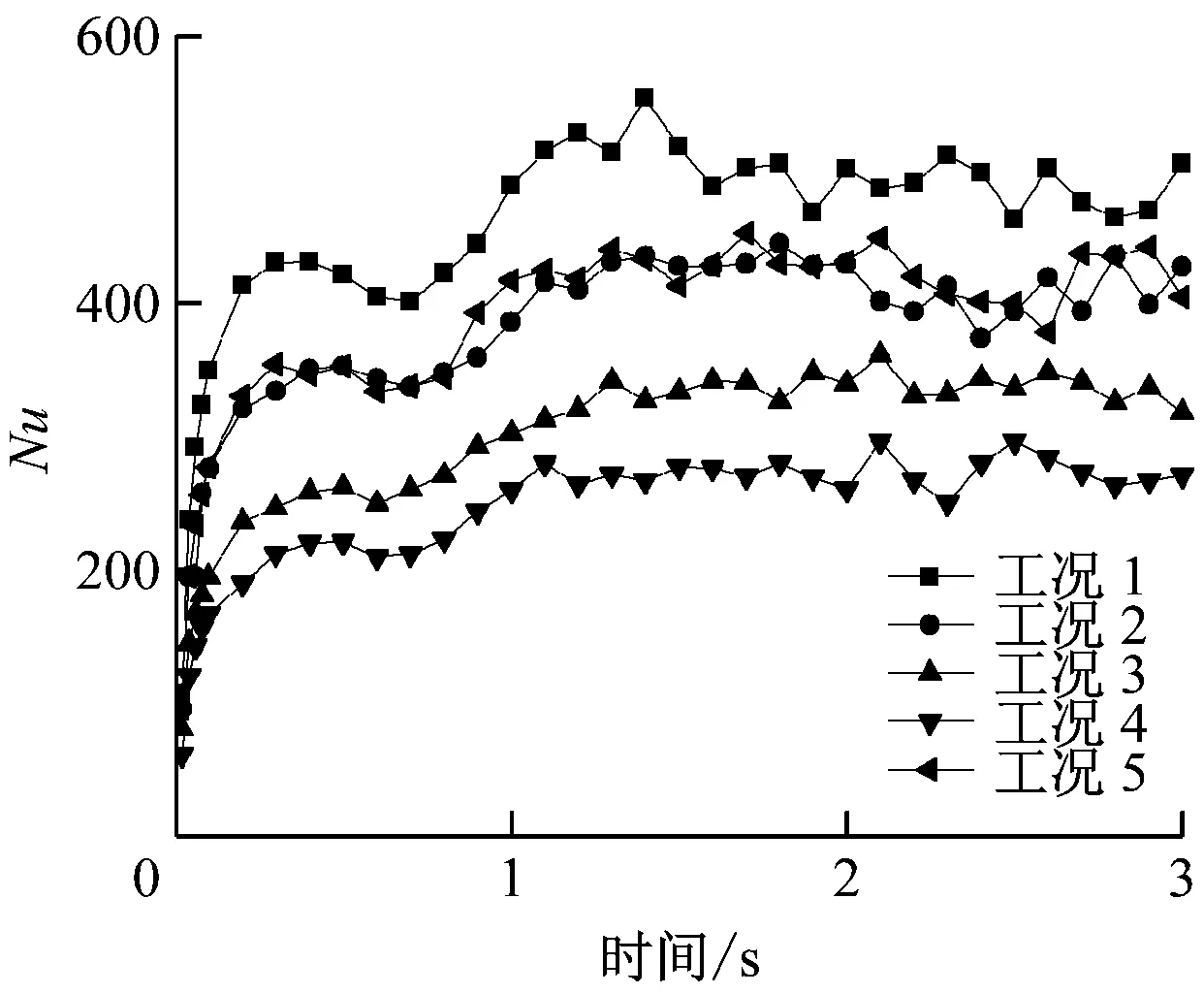
图11 不同工作条件下热管的传热系数
根据上述事实可知,在具有搅拌流和弹状流的加热管中,核态沸腾是给定操作条件下影响传热的主要机理。然而,这并不表明在大型管道中不存在强制对流沸腾。根据流型的分析可知,不稳定的弹状气泡存在于大型管道的顶部区域,形成薄的液膜。当弹状气泡存在时,相变主要发生在液膜表面。然而,弹状气泡并不稳定,很容易分解成搅混流。大气泡和壁面之间的小气泡部分来自弹状气泡的分解,部分来自加热壁面上的核态沸腾。
在分离式热管中,循环的总质量流量取决于重力压差。因此,工质的质量流量不能太大。在本计算中,从工作条件获得的质量流量区间为90~180 kg/h。在低质量流量和低热流密度的情况下,内径80 mm管道中的主要传热机制为核态沸腾,管外流体温度对传热强度影响较大,质量流量对传热强度的影响很小。
5 结 论
(1)在大型垂直管内工质流动和变化过程中观察到泡状流、弹状流和搅混流。弹状流和搅混流产生于加热管中气泡的生长和随后的聚集过程中。
(2)倾角对流型及传热的影响很大,随着倾角的减小,流动出现越来越明显的不对称特点。在倾角减小到60°后,相同的换热工况下,换热效果随着倾角的减小而越来越差。推荐分离式热管的蒸发段采取50°~80° 的倾角布置方式。
(3)在低质量流量和低热流密度的情况下,蒸发段管内主要传热机制为核态沸腾,管外对流传热系数和管外流体温度对传热强度影响较大,质量流量对传热强度影响很小。

