基于电子式互感器的基波相位同步算法研究
牟涛,樊占峰,杨智德,赵应兵,安永帅
(许继集团有限公司,河南 许昌 461000)
0 引 言
电子式互感器是智能变电站建设中重要的设备之一。目前电子式互感器主要分为采集一次电流信息的电流互感器和采集一次电压信息的电压互感器。电流互感器的一次传感头主要是罗氏线圈。电压互感器的种类比较多,依据其传感头的原理不同主要分为电容分压,阻容分压,电阻分压等类型。不同原理的传感头之间因为原理的不同,其等效电子回路的幅频特性和相频特性存在很大差别。其中罗氏线圈和阻容分压原理输出的是微分信号,需要后级对其模拟信号进行积分。通常电子式互感器测量精度要求普遍是0.2级,部分场合要求达到0.2 S级[1-2]。即使相同原理的传感头由于工艺及参数的离散性分布原因,也存在很大的误差。同时在模拟电子回路及AD采集,模数转换,数据处理的过程中同样会引入各种误差。如何消除这些误差,满足电子式互感器基波相位和副值的精度要求是我们要重点研究的问题[3]。
目前普遍的方案是在电子互感器的采集单元中采用模拟回路,对传感头输出的小信号进行相位和幅值的校正,并通过模拟积分回路对传感头的微分信号进行还原[4]。但是模拟回路的参数一般是固定的,不方便根据实际偏差进行调整,而且模拟回路容易受温度,电磁干扰等因素的影响,存在很大弊端[5-7]。在数字信号处理中,幅值的校正一般可以通过乘系数的方式消除,不存在难点。本文重点研究采用数字信号处理的方法对基波相位同步校正。目前应用最广泛的基波相位同步的处理方法是拉格朗日插值定理,常用的抛物线3点插值公式表示如下:
(1)
通过插值公式可以得出结论,采用拉格朗日插值定理进行基波相位同步,运算量较大,通过一般的嵌入式CPU来实现会非常占用资源。因此研究其他效率更高精度更好的相位同步的方法具有非常重要的意义[8]。
1 基于两点插值的相位同步算法
两点插值算法就是一种较简单的基波相位同步方法。其特性是利用数字滤波器的相频特性,对基波信号的相位进行调节,实现模拟工频信号的相位精度校正及同步。其传递函数如下:
(2)
转换为离散域的表达式如下:
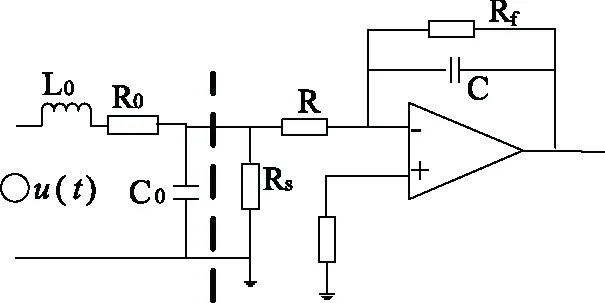
Y(n)=a×X(n)+(1-a)×X(n-1) ,(0 我们对系统进行仿真得出其幅频和相频特性如图1所示。 图1 两点插值的幅频和相频特性曲线Fig.1 Characteristic curve of two-point interpolation 通过仿真波形,我们可以看出,两点插值算法相频特性符合FIR滤波器相位线性度好的特点。因此采用两点插值算法来实现电子式互感器模拟量的相位校正是一个不错的选择。 图2是实际应用中,可调系数a在其调节范围0 图2 两点插值的幅值相位曲线Fig.2 Amplitude and phase curve of two-point interpolation 通过仿真可以看到两点插值的优势是算法简单,相位调节线性度好。但是缺点同样比较明显,那就是幅值偏差较大,而且可调范围比较窄,可调范围小于一个采样周期Ts。在实际应用中,两点插值算法在电子式互感器信号处理中,可用于相位的微调,但需要在相位同步的过程中对幅值进行补偿,以消除算法中的幅值误差。 针对两点插值法存在的幅值偏差大,可调范围较小的不足,我们研究了一种新的相位同步算法,其原型是一种经典的模拟运算放大器构成的相位校正电路。我们通过对电子回路进行一系列离散化变换得到一种新的相位同步算法[9]。 整个算法的模拟电路原型如图3所示,其参数R1=R3,R2采用可调电阻,其阻值和系统相位呈函数关系,其中0 (3) 式中Y1=R2×R3×C;Y3=R1×R2×C;Y2=Y4=R1。 通过双线性变换法,将其转换为离散域的传递函数,具体方法是将整个频率轴上的频率范围压缩到±π/T之间,再用z=esT转换到z平面上。 (4) 其离散域的传递函数为: (5) 为了提升算法的性能,同时克服算法相频曲线非线性的缺点,实现电子式互感器传感头和采集回路系数独立调节,我们将两级传递函数进行级联。设传感头系数为A,采集回路系数为B。经过卷积运算,原来的一阶系统转换为二阶系统其传递函数如下: (6) 通过分别调节系数A和B值,可以实现传感头和采集回路相位的精度校正。在实际应用中,通过两级系数的方法可以实现电子式互感器传感头和采集单元之间的免调试互换,提高电子互感器现场维护效率。 图3 移相滤波器模拟电路原型Fig. 3 The circuit of phase shift filter 通过Matlab仿真软件我们对系统的幅频特性和相频特性进行仿真,其仿真波形如图4所示,我们可以看出其幅频特性曲线为一条直线,相频曲线的过渡也非常平滑。 我们将传递函数转换为离散域的表达式为: Y(n)=A×B×[x(n)-y(n-2)]+(A×B)×[x(n-1)-y(n-1)]+x(n-2) (7) 通过Matlab对系数 -1 图5是系数A在整个可调范围内的幅值和相位特性曲线,A值对应横轴。我们可以看出在-0.5 图4 算法的幅频和相频特性曲线Fig.4 Amplitude-frequency and phase-frequency characteristic curve of the algorithm 图5 算法的幅值和相位特性曲线Fig.5 Amplitude and phase characteristic curve of the algorithm 本节所研究的算法相比较第一部分的两点插值法,在调节范围和幅值精度上有较大的优势,其不足是线性度没有两点插值算法理想,我们在应用中,设置两个系数A和B,分别用于传感头和采集器的相位补偿系数,可以弥补线性度的不足[10]。 电子式互感器的罗氏线圈及积分回路等效电路如图6所示,我们可以了解到,传感头的微分电路比较复杂,其中包括线圈的电感L0,杂散电容C0,负载电阻RS等参数,不同的传感头其参数存在着很大的区别。 图6 Rogowski线圈及积分回路等效电路Fig.6 Rogowski coil and integral loop equivalent circuit 虚线前端的罗氏线圈等效电路经过拉普拉斯变换得到的传递函数为[11]: (8) 由于不同的传感头存在着参数上的差异,因此采用固定参数的模拟积分回路或者数字积分算法很难满足要求,主要表现为对电子式互感器施加衰减直流分量,采集单元的输出难以完全还原真实的波形。另一方面无论是模拟积分,还是数字积分,因为存在饱和的问题,都不可能对微分信号实现90°的相位还原。因此积分后的基波信号往往存在几度的相位偏差,需要在积分算法中进行补偿。 我们首先计算出积分回路连续域的传递函数: (9) 将其通过变换转换为离散域传递函数如下[12]: (10) y(n)=A×{a×[x(n-2)-x(n)]+x(n-1)+ x(n)}-B×y(n-1),(0 (11) 式中参数A,B的值由一次传感头的参数决定,具体值需要根据传感头的模型来决定。参数a用于积分回路相位补偿,可调范围为TS,分辨率为1′。我们将220 kV罗氏线圈的参数代入传感头的传递函数,其中M=10.25 μH,R0=32.4 kΩ,C0=0.032 μF ,RS=288 Ω。计算出传递函数的实际值: (12) 经过参数匹配得到积分算法参数A= 0.041 654 ,B= 0.999 38 ,a= 0.02。将传感头和积分算法组成的模型通过MATLAB内部Simulink工具,对系统输入90°的衰减直流分量,其输入输出波形如图7所示,为了便于分析,我们特意把输出幅值加大1.1倍,可以看到输入输出波形暂态特性一致,算法能很好的满足电子互感器暂态特性的要求。 图7 积分算法对暂态波形的响应Fig.7 Response of the integral algorithm for transient waveform 重点讨论了两种数字信号处理方法在电子式互感器精度校正,特别是基波相位同步上的应用,提出了两种便于实现且性能可靠的相位同步算法。两种算法运算量小,相比较常用的拉格朗日插值定理实现相位同步的算法,能节省80%的运算量,方便嵌入式CPU和FPGA的实现。同时研究了数字积分算法针对不同的传感头进行相位补偿和参数匹配的问题。解决了电子式互感器由于数字积分参数与传感头参数不匹配导致的叠加衰减直流分量等暂态特性差及相位不同步的问题。研究采用数字方法实现对电子式互感器的基波相位同步,能够解决电子式互感器研发中存在的可靠性和精度校正方面的不足,对于电子式互感器未来的发展具有非常重要的意义。

2 基于模拟调相电路离散化的相位同步算法
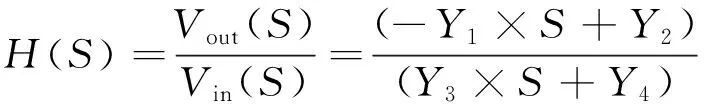

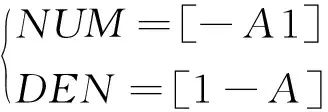




3 带相位同步补偿的数字积分算法

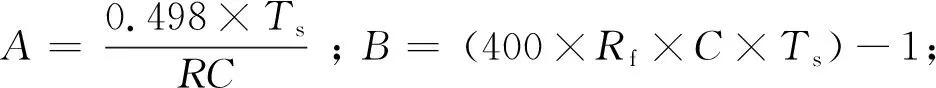


4 结束语

