基于动-静态混合算法的配电网绝缘子交直流污闪模型

，

(云南电网有限责任公司 电力科学研究院，昆明 650217)

0 引言

绝缘子污秽闪络是电网故障的主要原因之一，污闪通常是由积污绝缘子表面泄漏电流不断加剧造成的。污层的分布主要取决于环境因素、电场、绝缘子的污秽捕获位置以及绝缘子的材料[1-6]。积污严重程度主要取决于自然因素、积污来源(自然污秽、工业污秽、混合污秽)、污秽电导率以及降雨密度[7-8]。

目前对于泄漏电流的起始过程及其加剧发展为绝缘子闪络的过程已经有了较为详细的研究和了解，并基于闪络过程建立了各种闪络模型。问题在于目前针对绝缘子污闪过程的模型主要以静态或者动态电弧模型为主。静态模型虽然能从解析的角度求解临界闪络时的各种数值解，但不能模拟局部电弧发展的动态过程。静态模型同时忽略了注入污层的电气能量，但实际上大部分(60%～87%)的电源能量是用于加热污层以及水分的蒸发，使得传统污闪模型的应用受到一定限制[9-10]。针对该问题，本文的主要工作是利用等效电路的方法对染污绝缘子表面电弧产生以及发展直至闪络的过程建模分析，设计了一个计算电路元件参数的基本算法来建立静态模型描述电弧发展过程中的稳态过程，当满足电弧闪络的临界条件后，启用动态算法建立暂态模型来描述闪络过程。该模型能够描述影响绝缘子闪络的主要参数，例如电流、长度、半径、发展速度、线性电阻、温度。其中线性电阻本文使用解析方程计算以代替经验以及半经验方程。最后笔者就模型计算的结果和试验结果进行了比较，试验研究结果表明，该闪络模型计算结果与试验结果符合度较好。

1 等效电路参数的确定

本文采用的等效电路受Obenaus等效电路模型的启发。该等效电路由等效电阻Rd(轴向长度为Xd的圆柱形放电模型)和电容Cp与电阻Rp并联表示的污染层串联组成，见图1。图中泄漏长度(电极间隙)为L。

图1 污层串联放电模型Fig.1 Model of discharge in series with the non-crossed width of pollution layer

该模型包括3部分：第一部分可用来确定等效电路参数。该方法通过控制同一放电电流、电压及其相位角，对不同放电长度进行试验。再利用经验和半经验公式确定不同放电长度的放电电阻值以及污层电阻、电容值。当闪络发生时，污层的等效阻抗将为0。将上述计算方法得到的参数值在MATLAB软件中进行差值计算。本文建立如下2个方程：一是关于污层等效电阻的方程，二是关于污层等效电容的方程。总泄漏长度按照放电长度分为不同部分，并且本文针对每一部分从不同阶数的有理多项式、高斯公式、对数公式、幂公式中选择适当的公式，再结合放电电流值，最终确定放电电阻值。

由文献[11-13]的研究结果可知，电极处的电压降落可忽略不计。

从而，等效电路阻抗Zeq可表示为

(1)

式中：U表示施加电压值；Id表示放电电流。

(2)

或者

(3)

上式可写成以下形式：

Zeq=Zp+jZq

(4)

(5)

(6)

式中，Zp和Zq分别表示电路等效阻抗的实部和虚部，与施加电压与放电电流的相角有关。

式(6)与式(5)相除可得，

(7)

式中：

(8)

再将式(8)代入式(5)，可得

(9)

式中，

(10)

放电电阻Rd可由式(11)通过放电电流和长度Xd得出[10]。

(11)

式中，A和n为闪络常量。

综上所述，放电通道的半径可认为是常数，并可用Mayer方程来计算放电电阻。而在实际情况中，放电通道半径随电流的增大而增大。笔者认为放电通道半径为常数。图2展示了计算步骤流程图。

图2 等效电路参数识别算法框图Fig.2 Chart of the equivalent electric circuit parameters identification algorithm

2 闪络的静态模型

闪络过程的第一阶段处于稳态模式。在这一阶段中，电压的增加将引起放电长度的增加。下面将介绍闪络静态模型中用于确定放电参数的各方程。

在交流高压闪络后发生放电重燃时，有[14-15]

kXd=UIdn

(12)

式中，k是放电起始常数，可由式(12)代入式(1)得到：

(13)

或者

(14)

按照上文计算方法，等效阻抗Zeq取决于放电长度。在此，本文定义了与给定电压值相关的变量。

在直流情况下，不考虑电容的影响。从而，系统两端的电压可表示为

U=(Rd+Rp)Id

(15)

式中：

(16)

(17)

式中，ρp和ρd分别代表污层及放电通道的电阻率。从而污层的线性电阻rp和放电通道的线性电阻rd可表示为

(18)

(19)

放电扩散的临界情况可表述为

(20)

或者

rp=rd

(21)

从式(16)、(17)及(20)可推导出：

(22)

将式(22)代入式(15)可得，

(23)

再结合式(11)，放电电压可表示为

(24)

由式(22)和(24)可推导出：

(25)

式中

(26)

因而，电流Id可表示为

(27)

再将Id代入式(23)，结合式(22)和(27)可得：

(28)

即

(29)

利用第一种计算方法，确定了污层电阻与放电长度的关系。对于不同电压取值的情况，见式(29)。

为计算放电半径，可用以下关系：

(30)

为计算放电温度，有学者认为，总放电能量通过放电通道的热传导耗散。根据傅里叶热力学定律，单位长度的能量P为

(31)

式中，Ed、Id、Q、λth、Aiso、un和Td分别代表放电电压梯度、放电电流、热量、热传导系数、放电过程的等温面元、放电过程温度梯度的方向分量和热离子化所需的轴向温度。

本文的研究基于以下假设：1)放电通道的等温面为半球状且温度扩散方程为单维度；2)放电处于局部热力学平衡(即系统的不同部分间不存在温度梯度或压力梯度且不存在化学成分的变化)中，能量平衡可表述为

P=EdId=πλthTd

(32)

根据欧姆定律：

(33)

式中：σd、Sd、ρd和Jd分别代表放电电导率、放电截面、放电电阻率和电流密度。

结合式(19)、(32)、(33)，可得：

(34)

其中放电线性电阻rd可由式(35)得出：

(35)

将式(35)代入式(34)，可得：

(36)

一般来说，大部分学者利用Mayer方程来表述放电线性电阻的动态变化过程：

(37)

上述方程不适应于静态情况。Mayer方程还假定放电半径为恒定值，而与符合实际情况的式(30)相反。

从另一方面来说，由(3)式可知，系统的等效阻抗可表述为

(38)

将式(1)和式(38)代入式(34)可知，放电线性电阻rd等于放电电阻Rd除以长度Xd：

(39)

或

(40)

其中

a=1+ω2Cp2Rp2

(41)

最终可得二次多项式方程，其中放电电阻Rd未知：

(42)

该方程的判别式Δ为

(43)

方程的两个解为

(44)

(45)

当闪络发生时，有

Xd=LU=UcRp=0

(46)

Uc代表闪络电压。

此时，有

Rd1=0 Ω/m

(47)

(48)

从而相应的线性电阻可表示为

rd1=0 Ω/m

(49)

(50)

对于第一种情况(rdl=0)，电流和温度将趋于无穷，与实际不符。对于第二种情况(rd2≠0)，将其代入式(39)可得

(51)

由Rd=rdL以及Id=Uc/Rd

可得

(52)

该关系式与前文得出的等式(34)一致。故选择Rd2作为方程(42)的解。因而下文所用的放电线性电阻rd=rd2。

(53)

在直流情况下，等式可简化为

(54)

上述关系式由理论分析得出，与文献中基于经验及半经验得出的方程相反。图3的流程图描述了上述静态模型。

图3 静态模型流程图Fig.3 Chart of static model

3 闪络的动态模型

一旦达到闪络的临界条件，放电将进入不稳定阶段，将最终导致跳变以及整个泄漏长度的交叠。上述情况将由动态模型描述。描述前一阶段的静态模型的最终值作为该动态模型的初始值。

为计算放电扩散速度，运用Beroual方程：

(55)

式中：β是注入系统并用于放电的电能(功率Pt)的比率，取值范围为0.05～0.10；ρ是密度；ad是放电半径。

考虑到放电长度，利用动态模型计算方法进行dt的迭代计算。在每次迭代过程中，新的放电长度Xd(i+1)将等于前一放电长度Xd(i)与vd(t)·dt。

Xd(i+1)=Xd(i)+vd(t)dt

(56)

式中，i表示迭代次数。

图4给出了动态模型的流程图。

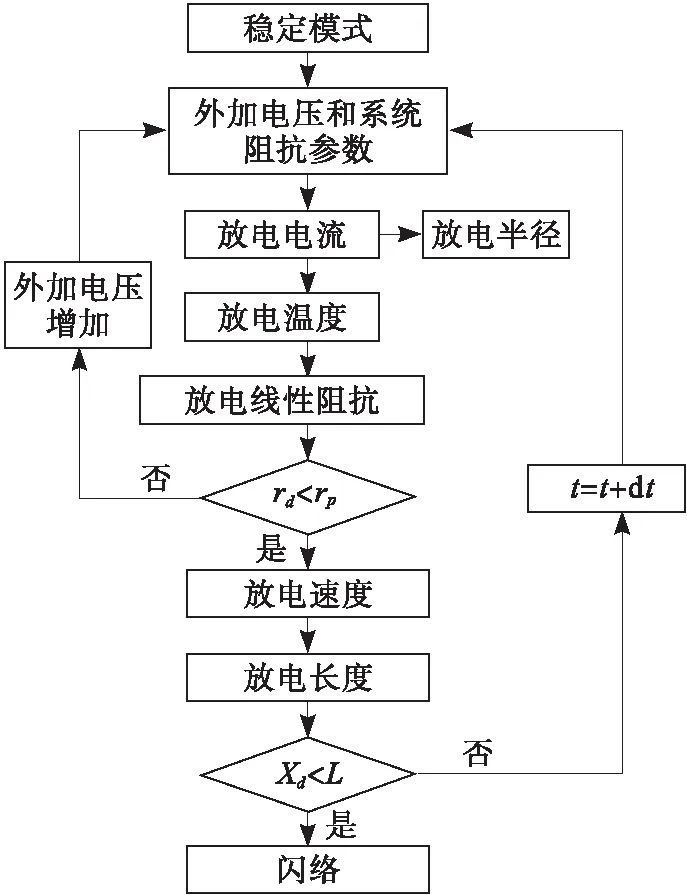
图4 动态模型流程图Fig.4 Chart of dynamic model

4 模型的试验验证

为验证前节提出的模型，需比较放电长度试验结果与施加特定的交流电压下的计算结果，即放电长度和放电电流的比较。

试验设备包括：试验变压器(500 V/300 kV，50 kVA，50 Hz)、拍摄闪络过程的可视化相机(SONY DCR-SR)、与计算机相连的数字示波器以测得电压和泄漏电流参数与波形。

试验样品是覆有潮湿沙子的玻璃制平面(500 mm×500 mm×5 mm)。电极由两个铝片(500 mm×3 mm×0.003 mm)制成，一个电极与试验变压器相连，另一电极与地线相连。泄漏长度(即电极间距)为292 mm。试验平台示意图见图5。

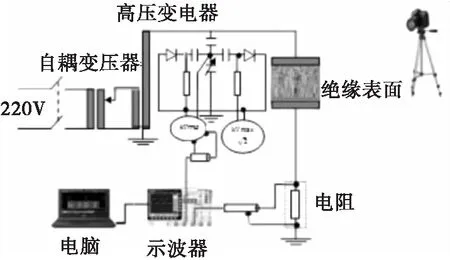
图5 试验平台示意图Fig.5 General view of experimental device

试验污层所用的沙子样品取自我国西北沙漠地区。其一是粒样品一号，0.0308 g/cm2单位灰密沙子其表层电导率为30 nS；其二是沙粒样品二号，0.020 5 g/cm2单位灰密沙子其表层电导率为23 nS。沙层还需15 ml蒸馏水进行喷雾处理。

图6和图7绘制出试验得到的施加电压及电流和放电长度的关系曲线，并与本文仿真结果进行对比。仿真结果通过Matlab 2015a得到。经对比分析可得，试验结果与仿真结果表现出较好的一致性。从而，笔者建立的模型能够较好地描述污闪模型。随后，笔者将改变特征参数进一步研究污闪放电问题。

5 仿真及结果

5.1 放电长度

在稳态阶段，针对不同污层施加不同的高压。对于沙粒样品一号砂层，施加在绝缘子上的电压从10 kV升至90 kV；而对于沙粒样品二号砂层，施加在绝缘子上的电压从10 kV到98 kV。显然，放电逐渐发展直到临界长度为12.3 cm(90 kV，沙粒样品一号砂层)和15.9 cm(98 kV，沙粒样品二号砂层)，见图8。以上两种情况的放电长度及施加电压临界值的差异是由于沙子化学成分不同引起的，其中沙粒样品一号砂层电导率更高。当满足临界条件时，放电将进入不稳定阶段，直至放电长度等于总泄漏长度，见图9。

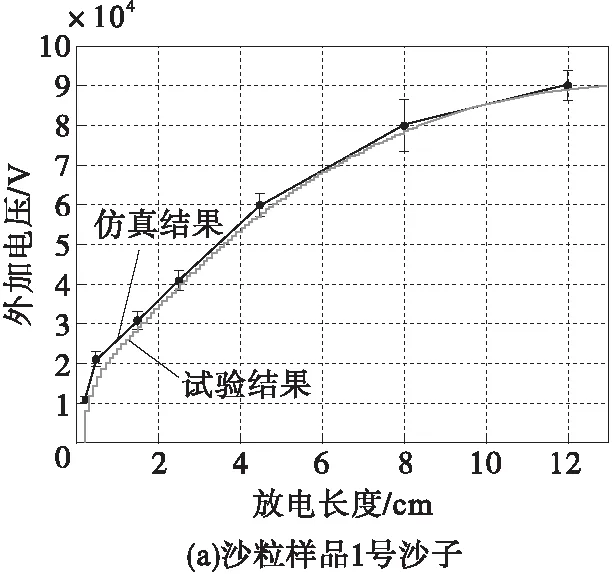
图6 施加电压及电流与放电长度的关系Fig.6 Applied voltage and current verses discharge length for bechar sand

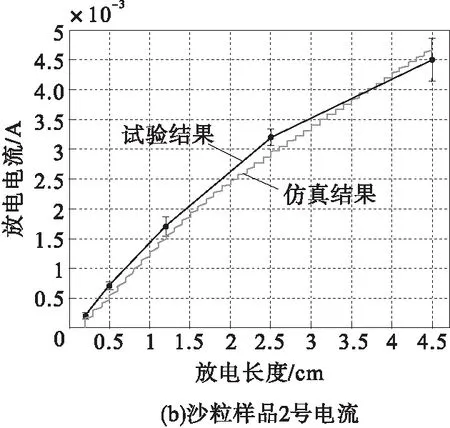
图7 沙粒样品2号电压(a)与电流(b)和放电长度的关系Fig.7 Voltage(a) and current(b) verses discharge length for Boussaada sand

图8 稳态模式下施加电压与放电长度的关系Fig.8 Applied voltage verses discharge length during the stable mode

图9 非稳态模式下放电长度随时间的变化Fig.9 Temporal evolution of the discharge length during the unstable mode

5.2 放电电流

电流与放电长度的关系曲线见图10。可明显看出，当放电长度达到2/3总泄漏长度之前，电流逐渐增加；放电长度最终增至等于总泄漏长度的过程中，放电处于不稳定阶段，电流急剧增加直至发生闪络。当放电扩散时，污层阻抗与放电电阻均增加。在放电长度超过1/2总泄漏长度后，沙粒样品一号砂层表面的放电电流大于沙粒样品二号砂层表面。

放电电流特性取决于施加电压以及污层的电导率。从而，发生污闪期间流过两砂层试品的放电电流不同。

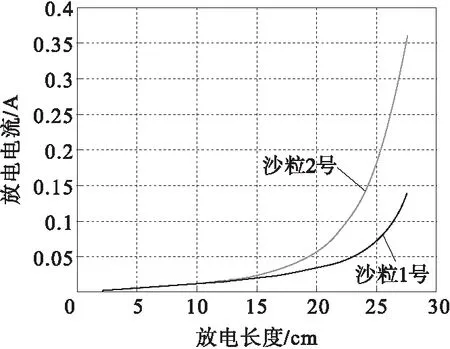
图10 放电电流与放电长度的关系Fig.10 Discharge current verses discharge length;

5.3 放电半径

由式(30)可知，放电半径与放电电流有关。对于两砂层试品，均出现当放电长度增至2/3泄漏长度时，放电半径逐渐增加，而到放电长度最终等于总泄泄漏长度时，放电半径急剧增加，见图11。此外，沙粒样品一号砂层的放电半径较高。

图11 放电半径与放电长度的关系Fig.11 Discharge radius verses discharge length

5.4 放电温度

由图12可知，放电电流的增加将导致放电通道及其附近区域温度的升高。仿真得出的放电温度与文献[15-16]的放电温度范围相同。

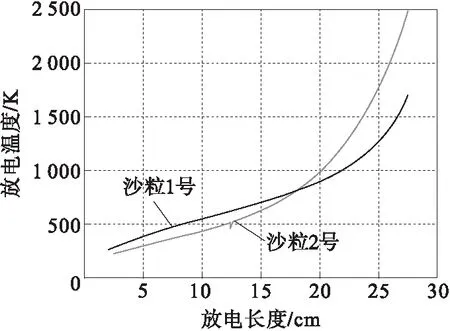
图12 放电温度与放电长度的关系Fig.12 Discharge temperature verses discharge length

5.5 放电线性电阻

当放电开始扩散时，其线性电阻rd急剧减小，见图13。当放电长度从2 cm增加到10 cm时，沙粒样品一号砂层的线性电阻减小了其初始值的95%。随后，线性电阻值的减小取决于闪络过程。线性电阻的减小遵循于Dhahbi等人提出的扩散准则以及Fridman等人提出的等式。

5.6 放电扩散速度

图14给出了放电扩散速度与放电长度的关系。易知，在稳态阶段(对于沙粒样品一号砂层来说，放电长度在12.3 cm之前；对于沙粒样品二号砂层来说，放电长度在15.9 cm之前)，放电过程稳定。随后，放电进入不稳定阶段，并且放电扩散速度急剧增加至数百米/秒。

图13 放电线性电阻与放电长度的关系Fig.13 Discharge linear resistance verses discharge length

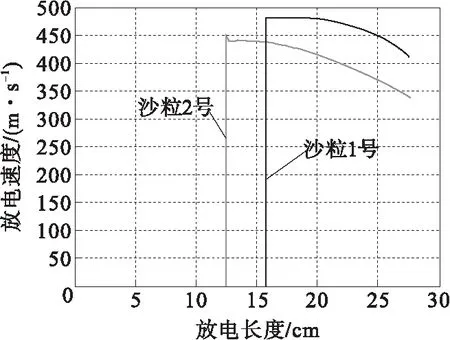
图14 放电扩散速率与放电长度的关系Fig.14 Discharge propagation velocity verses discharge length

6 结论

提出的模型可较好地描述直流和交流情况下染污绝缘子表面放电直至闪络的各个阶段。该模型基于放电等效电路以及经验分析、半经验公式，可计算放电过程中的主要特征参数，并可分析出特征参数随试验条件改变的变化过程。此外本文还建立了放电线性电阻与放电温度、施加电压、放电长度和污染参数的关系，尽管迄今为止相关研究均是基于经验和半经验公式得出的。研究表明，污层类型将影响电流，还可加快放电半径、线性电阻及放电通道温度的变化。