基于改进TOPSIS法的水资源确权分配模型及应用研究

，，

(1. 江苏省连云港市赣榆区城头镇水利管理服务站，江苏 连云港 222100；2. 江苏省连云港市赣榆区水利局，江苏 连云港 222100；3. 江苏省连云港市赣榆区机电排灌管理站，江苏 连云港 222100)

水资源短缺是制约着我国社会经济发展的重要矛盾，其最根本、最有效的解决措施是建立节水型社会，节水型社会是以建立水权制度为管理基础，水市场的发展与水体系的完善必须进行水资源确权，水资源确权即是水权分配的合理界定，也是水资源优化配置和水资源统一调度管理的重要前提[1]。

水权分配就是一个水资源量的分配，水量代表的是水权多少的虚量，而不是以水量为载体的份额，同时又具有多复杂、多系统、多目标的决策问题。目前，相关的研究成果主要是以水权概念、制度、指标体系和管理措施等方面的宏观上的定性描述，在定量分析方面的研究尚未完善，定量分析常用的传统方法主要有层次分析法、模糊综合分析法、主成分分析法、常规TOPSIS法的等，由于存在人为主观性，因此，在传统研究方法的基础上运用高维空间、非线性、多目标决策系统进行精确度的提高，如CRITIC法、投影寻踪法、可拓物元法等[2-5]。这些方法中层次分析法易受到经验专家的人为影响，模糊综合分析和可拓物元法受到数学函数和模式化局限性，投影寻踪法模型构造复杂，计算量较大，因此，本文在常规TOPSIS法的基础上进行改进，避免“欧式距离”带来的一些缺陷，并采用综合均衡的权重值，建立改进的TOPSIS法水权分配模型，为城市的水资源统一规划与管理奠定了基础。

1 改进的TOPSIS法

1.1 垂直距离的改进计算

TOPSIS法是运用在水资源分析与评价中常用的多目标决策方法。其中正交投影法就是运用垂直距离作为贴进度计算的基础，以确定作为方案的依据，弥补了常规TOPSIS法的缺陷。垂直距离是指理想解与负理想解连线作为法向量，分别垂直法向量做两解的平面，即理想解与负理想解平面之间的距离[6]。在所有评价指标中 ,与理想解距离最近同时与负理想解距离最远的指标，即为最佳指标，反之为最差指标。

1.2 评价指标权重的综合集成

确定评价指标的权重也是改进的TOPSIS法关键步骤，本文将主观方法与客观方法相集成与融合，即采用层次分析法[7]与变异系数法[8]相结合，最终得到一个综合均衡的权重值。

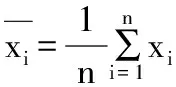
(1)

根据变异系数法公式计算评价指标变异系数：

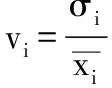
(2)

评价指标变异系数权重计算公式：

(3)

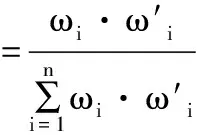
(4)

其中，ωi′为层次分析法求得权重值，ωi*为综合均衡权重值。

1.3 改进的TOPSIS法计算步骤

结合正交投影法和层次分析法与变异系数法相结合的综合均衡权重的改进TOPSIS法的构建模型步骤如下[9-10]：

1.3.1 构造原始决策矩阵

假设有n个评价对象，m个评价指标，组成评价方案集合A=(A1，A2，L，An)，指标集合B=(B1，B2，L，Bm)，指标集合在评价方案集A下构造原始决策矩阵X：

1.3.2 原始决策矩阵数据标准化

评价指标具有越大越优型和越小越优型，各个评价指标由于量纲不同，为了消除各指标间的量纲，采取对原始数据进行归一化标准处理，形成标准化矩阵Eij，具体如下：

(5)

(6)

其中，e(i，j)为归一化标准，xmax(j)为第j个指标的最大值，xmin(j)为第j个指标的最小值。

1.3.3 构造加权矩阵

1.3.4 求得理想解Y+和负理想解Y-

通过构造的加权矩阵，确定理想解和负理想解，其中包括效益型指标集和成本型指标集，具体公式如下：

(7)

(8)

1.3.5 计算垂直距离

理想解与负理想解平面之间的距离对所有评价对象都是相同的，代表是一种范数，因为各评价对象与理想解之间的距离按下式计算：

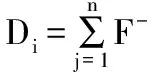
(9)

Di值的大小代表着理想解的程度，Di越小，评价对象越优，反之，Di越大，评价对象越差。运用到水权确定当中，代表着供需水量的程度，Di越小，需要分配的水量就越大，设以Di最小值为标准，进行多样本比较得到相应的分水比例，再与总水量的乘积得到各部分的分水量。

2 实例应用

2.1 实例概况[11-12]

连云港位于江苏省东北部，地处北纬33°59′～35°07′、东经118°24′～119°48′，由于处于暖温带南部，四季分明，冬季寒冷干燥，夏季高温多雨，常年平均气温14℃。连云港市地处淮河流域的沂沭河下游，辖区分属沂河水系、沭河水系和滨海诸小河水系，年降水量814.1 mm，径流深138.9 mm，全市水资源总量16.30亿 m3，其中，地表水资源量10.58亿 m3，地下水资源量5.72亿 m3，平均产水系数为0.26，水资源利用率达40%，全市入镜水量与出境水量比为1:1.45。全市总用水量26.40亿 m3，其中，生产用水占总用水量的91.9%，生活用水占总用水量的7.5%，生态环境用水占总用水量的0.6%，生产用水中最多的是农业用水，占总用水量78.8%，亩均农田灌溉用水量412.1 m3，灌溉水利用系数0.59。

随着连云港市社会经济的快发发展，经济的发展带动着对水量需求的增加，由于水环境恶化的矛盾日益突出，进行需要进行初始水权分配对城市水资源合理配置、生态环境保护等方面具有重要的意义。以2016年为基准年，对连云港市在不同频率下的来水进行水权分配，根据总水量的标准，确定的分水总量为23.76亿 m3。

2.2 评价指标体系构建

水资源水权分配主要是依据评价指标进行确定分水权重，评价指标体系的建立综合反应了连云港市在水资源优化配置与高效利用的基本情况和发展规模，同时也说明了评价指标之间具有一定的相互联系和相互独立。通过分析连云港市水资源供需态势，参照全国水资源供需分析体系，充分考虑不同区域水资源自然条件及开发利用方式的差异，从不同体系、不同层面选取具有科学性、代表性强、操作性、易于量化和对比性的指标准确的反应系统动态变化[13]。本文通过相关的研究成果并根据评价指标的选取原则[14]，综合考虑水资源开发用、社会效益、经济效益、生态环境效益等方面，以市区、东海县、灌云县、灌南县为评价对象，选取12个具有代表性的评价指标，建立评价指标体系，见表1。

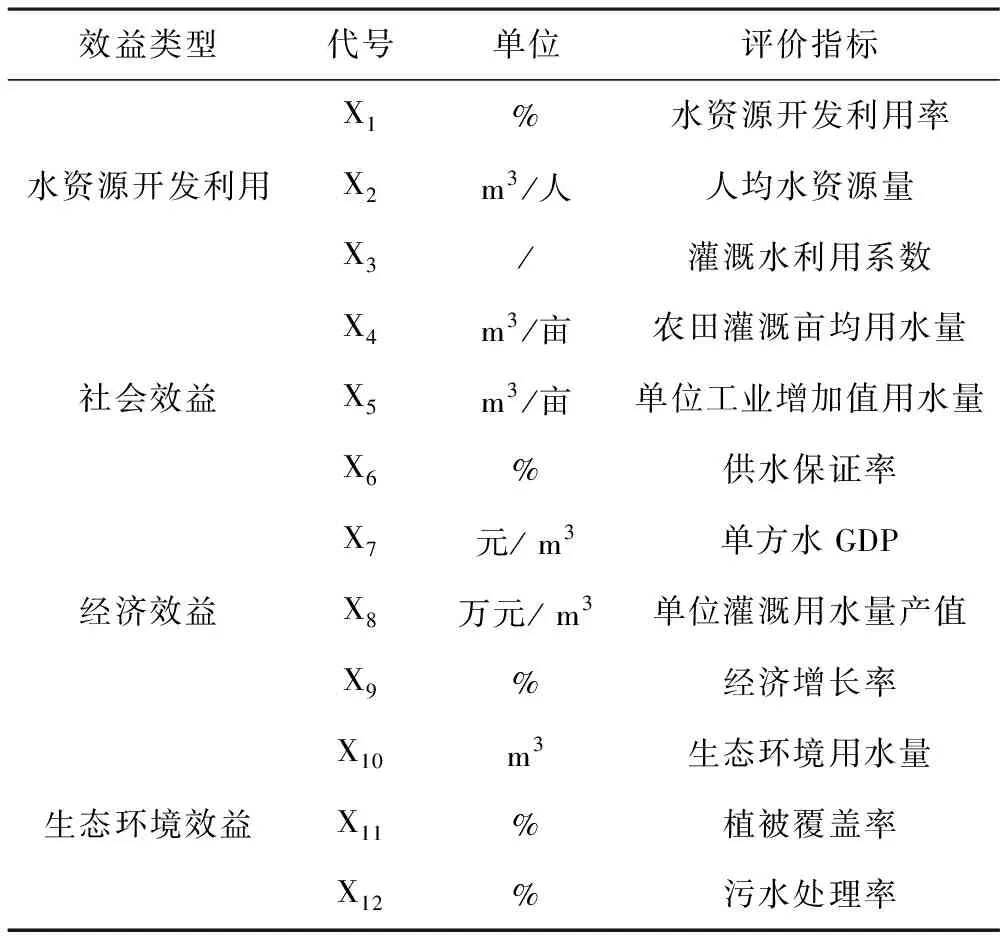
表1 水权分配评价指标体系

2.3 分水量计算

通过利用公式(5)和公式(6)对原始数据进行归一化标准处理，得到评价指标的标准化值，并形成原始决策标准化矩阵Eij。

各个评价指标权重计算分别运用层次分析法确定权重和变异系数法确定权重，计算结果见表2。

表2 各个评价指标权重

根据表2的计算结果，对层次分析法进行一致性检验，水资源开发利用、社会效益、经济效益、生态环境效益的CR<0. 1，则所求权重通过一致性检验，利用公式(4)进行权重综合集成计算，得到综合权重值：

ω*=(0.027，0.069，0.024，0.115，0.069，0.114，0.166，0.077，0.111，0.036，0.052)

进而构造加权矩阵F：

根据得到的加权矩阵F，按照公式(7)和(8)，计算理想解和负理想解，计算结果如下：

理想解：Y+=(0.017，0.039，0.012，0.077，0.039，0.066，0.076，0.105，0.043，0.060，0.020，0.027)

负理想解：Y-=(0.011，0.031，0.011，0.051，0.025，0.055，0.069，0.061，0.037，0.055，0.015，0.007)

考虑到计算的简便，将理想解平移到坐标原点，根据平移坐标的原则，各个区域的指标与负理想解计算结果见表3。

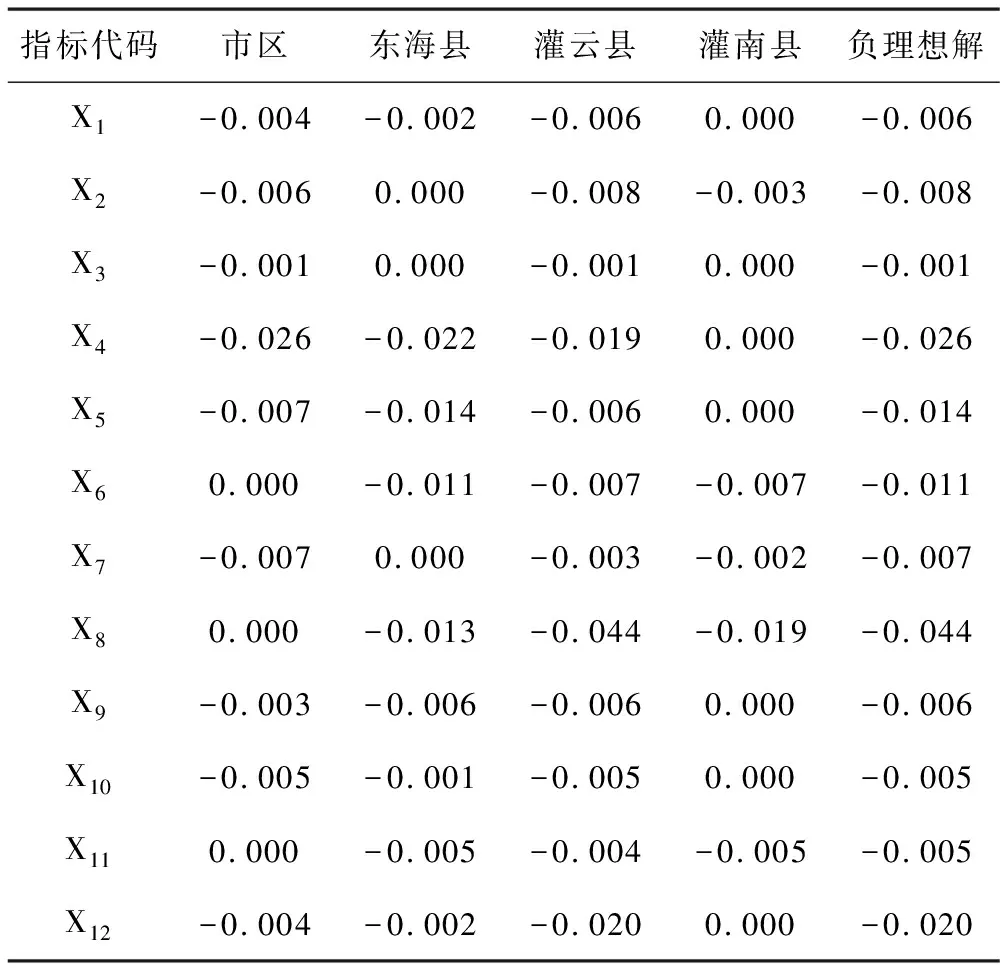
表3 平移后的计算结果

按照公式(9)进行计算，得到市区、东海县、灌云县、灌南县与理想解的距离为：

D=(0.001 025，0.001 588，0.003 184，0.000 981)。

2.4 结果分析

通过模型计算与分析，将市区、东海县、灌云县、灌南县计算出来的垂直距离由小到大进行排序，得到灌南县<市区<东海县<灌云县，D值的大小代表着理想解的程度，D越小，评价对象越优，对于水权分配来讲，对需水量和供水量程度就越大，反之，D越大，评价对象越差，需要的水量就越少。由此可见，以最优的结果为标准，与其他地区进行比较分析，得到市区、东海县、灌云县、灌南县分配水量的比例为0.274:0.195:0.162:0.369，相对应的分水量为市区6.51亿 m3，东海县4.63亿 m3，灌云县3.85亿 m3，灌南县8.77亿 m3。

为了验证改进的TOPSIS法在水资源确权中计算的准确性和优越性，将采取与常规的TOPSIS法、主成分分析法计算结果进行比较，见图1。

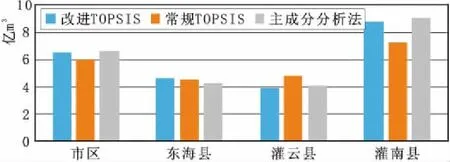
图1 不同计算方法结果对比

根据连云港市近10 a的水资源统计结果，在整个行政分区内，市区、东海县、灌云县、灌南县平均用水量比例为0.271:0.200:0.169:0.360，与运用的改进的TOPSIS法计算的得到的分水比例比较接近，符合该城市的水资源优化配置与高效利用的原则。通过图1的结果对比，说明常规TOPSIS法有较大的差距，特别是在灌云县和灌南县两个区域的分水比例与往期相差较大，结算的结果与实际情况不符，不具有客观性，因为常规TOPSIS法的理想解和负理想解是以理想贴进度的欧式距离进行计算，与理想解和负理想解的关系表现不明显，计算结果存在不合理性。与主成分分析法相比较，改进的TOPSIS法也表现优越性，这是因为主成分分析法存在评价指标部分信息损失问题，主成分是一个综合指标，具有一定的模糊性，没有原始变量的含义那么清楚、确切。改进的TOPSIS法运用的水资源确权分配水量计算模型兼顾主观与客观实际情况，得到计算结果均衡，与实际情况基本一致，显示了模型的准确性和科学性。

3 结语

近年来，连云港市在水资源合理分配与保护方面加大建设力度，加强用水总量控制，加强节水型社会建设，进一步加强地下水管理，推进水生态保护与修复，同时也落实完善最严格水资源管理考核机制。

在分析城市水资源确权模型和计算方法的基础上，对常规的TOPSIS法进行改进，垂直距离取代欧式距离进行计算，为了避免单一权重计算的局限性，采用两种互补的方法进行综合权重集成与融合，并运用到初始水权分配方法中，该方法的运用对水权模型建立提供了一种新的理念和思路。目前评价指标体系的研究未形成一个完整的理论体系，选取什么样的指标能全面的代表水权分配标准需要进一步深入的研究。