粤港澳大湾区核心城市房价传染与联动的市场逻辑

郭文伟

（广东财经大学金融学院，广州 510320）

一、引 言

在2017年3月5日召开的十二届全国人大五次会议上，国务院总理李克强在政府工作报告中提出“要推动内地与港澳深化合作，研究制定粤港澳大湾区城市群发展规划，发挥港澳独特优势，提升在国家经济发展和对外开放中的地位与功能”①。这意味着粤港澳大湾区建设已经成为重要的国家战略。粤港澳大湾区包括了珠三角9市（广州、深圳、佛山、东莞、惠州、珠海、中山、肇庆、江门）、中国香港特别行政区和中国澳门特别行政区。从地理位置来看，香港毗邻深圳，而澳门与珠海相邻。随着港珠澳大桥的正式通车，粤港澳大湾区各城市之间的基础设施将日趋完善，该区域内1个小时都市圈将会形成，这将会进一步加快建设国际一流大湾区和世界级城市群的进程。目前粤港澳大湾区的建设规划方案已经出台，随着该方案的逐步推进和落实，该区域内各城市在资金、物流、人才、产业等方面的融合将进一步增强，这种城市间的融合也会加强各城市房地产市场的融合。在这种背景下，各城市住宅价格势必会相互影响，尤其是那些地理相邻、存在紧密经贸往来的经济发达城市（比如：香港、澳门、广州与深圳）。随着大湾区内经济一体化的加深，香港和澳门高房价的外溢效应势必会影响与其存在频繁经贸往来或地理相邻的城市，进而加剧大湾区内各城市房价波动的传染效应。在目前中央政府致力于抑制房价泡沫、防范和化解系统性金融风险的大背景下，进一步厘清粤港澳大湾区内城市房价的时变联动性、房价波动传染效应及其市场逻辑，是一项值得研究的重要课题，相关研究结论能为制定科学合理的大湾区城市建设规划、防范大湾区内各城市房价泡沫交叉传染等问题提供有益的启示。

二、文献综述

由于粤港澳大湾区战略提出时间较短，从现有文献来看，鲜有关于粤港澳大湾区房价联动性及其传染效应方面的研究。现有的少数文献主要集中研究两方面问题：一是研究珠三角区域内住宅价格差异性、联动性及其泡沫测度。左夏伟和谢昌浩通过构建面板数据模型来分析 “泛珠三角”9省区房地产市场的差异性及其原因[1]。中国人民银行佛山市中心支行课题组分别采用两种方法 （基于住房可支付性指数方法和基于居民预期的住宅价格泡沫测度方法）对珠三角9城市住宅价格泡沫进行测度，结果表明珠三角9市均存在程度不一的住宅价格泡沫，其中深圳、广州和珠海名列房价泡沫程度前3名，而肇庆住宅价格泡沫程度最小[2]。陈章喜和黄准首先采用格兰杰因果关系分析了广州、深圳和东莞三个城市住宅价格之间的相互影响关系，在此基础上采用向量自回归分析了三者房价之间的脉冲响应特征，其研究结果表明广州和东莞的房价互为格兰杰原因，而深圳房价分别是广州房价和东莞房价的单向格兰杰原因。深圳房价对广州和东莞的房价带动效应较大，而广州和东莞的房价对深圳房价影响较小[3]。陈英楠和陈建也发现广州和深圳的住宅价格波动具有顺周期协同性[4]。杨元梅和谭术魁以珠三角9市为例，通过构建实证模型来揭示影响城市住宅价格波动的关键因素，其研究结果表明城市经济规模（GDP）是其住宅价格波动的最主要因素，且两者呈双向因果关系；另外，人均可支配收入和土地价格均对住宅价格产生正向影响[5]。曾晖采用BEKK-GARCH模型研究了深圳、广州和珠海在2008～2014年期间的住宅价格波动特征及其相互之间的波动溢出效应，其研究结论表明这三个城市住宅价格波动特征明显且具有周期性，其中珠海住宅价格波动最为激烈。广州与深圳住宅价格存在较为显著的波动溢出效应，且均对珠海住宅价格具有显著影响[6]。二是有关粤港澳大湾区内发展路径、定位、合作、融合等问题的研究。黄晓慧和邹开敏分析了“一带一路”实施背景下粤港澳大湾区各城市在文化、商业和旅游等领域的融合发展机制及对策[7]。陈朝萌分析了粤港澳大湾区内各城市港口的地位、层次和功能界定问题[8]。申勇和马忠新采用主成分分析法测度粤港澳大湾区和杭州湾区的开放度，并与世界三大湾区（纽约大湾区、旧金山大湾区和东京大湾区）进行多方面比较，研究结果表明：我国两大湾区开放程度较高，对其附近的城市区域具有明显的经济引领作用。相比世界三大湾区，我国的两大湾区经济规模居中，但在区域融合、产业创新等方面还存在明显差距[9]。纪春礼和曾忠禄基于智慧专业化理论来探讨粤港澳大湾区的创新协同路径和方向[10]。陈相针对粤港澳大湾区的区域和制度限制，探讨如何实现整个湾区财政科研经费的跨境使用[11]。

在分析城市房价空间传染方面，国内外学者基本集中在采用空间计量模型来分析城市房价的空间自相关特征 （空间依赖性）。Ismail[12],Kim和Goldsmith[13]通过实证分析发现COMADI区域内房价存在显著的正向空间相关性，并认为城市房价会受到相邻城市房价的影响。在国内，基于空间计量模型来分析房价的空间分布规律和传染效应已逐渐成为学术界研究热点。王春艳和吴老二研究发现珠三角城市房价存在明显的空间自相关性[14]。其他学者也分别采用空间自回归模型、空间误差模型、地理加权回归模型、广义回归模型等来分析我国不同区域或全国层面上的城市房价空间自相关性，所得结论较为相近，均认为我国各区域内城市房价具有显著的空间依赖性，空间因素对房价影响较大[15][16][17][18][19]。

尽管上述研究已经对珠三角区域或全国层面上的房价空间分布特征做了富有成效的分析，但由于粤港澳大湾区战略提出时间不长，至今鲜有文献对粤港澳大湾区核心城市之间房价联动性、房价波动传染效应进行专门研究。对此，本文以粤港澳大湾区内最具代表性的4个经济发达城市（广、深、港、澳）为研究对象，采用动态相关性系数模型（DCC）来测度四城市之间房价传染与波动的市场逻辑。在此基础上，采用R-Vine Copula模型和格兰杰因果关系法揭示各城市房价的相依结构、传染效应、因果关系。本文的特色在于：第一，首次基于DCC方法动态测度广深港澳房价的时变联动性；第二，采用R-Vine Copula模型揭示广深港澳房价之间的复杂相依结构及其波动传染机制。此研究将为构建粤港澳大湾区房价调控协同机制，制定科学合理的房价泡沫抑制政策提供有益的借鉴。

三、城市房价联动性及其传染效应测度模型

（一）时变联动性测度：DCC模型

经检验发现本文的房价指数序列并不适合采用GARCH模型来进行建模分析，而适合ARMA模型，因此本文采用ARMA(1,1)模型来作为DCC模型的边缘分布模型：

上述边缘分布模型有4个参数，其中参数c0和c1为常数项和收益率的滞后一阶的AR回归系数，c2和θ1为波动率的常数项及其滞后一阶的MA回归系数，εi,t为收益率系列的残差。DCC-ARMA模型形式如下：

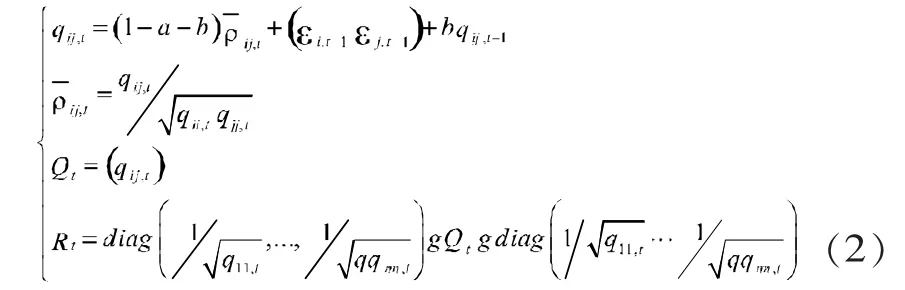
公式（2）中，ρij,t为 εi,t和 εj,t之间的无条件相关系数，Rt为时变相关系数矩阵，a和b为DCC模型测度时变联动性的待估参数，且需满足a+b＜1的约束条件。

（二）房价波动相依结构和传染效应测度模型：R-Vine Copula

目前学界出现了三种构建高维Vine Copula模型的主流方法：C-Vine Copula、D-Vine Copula、RVine Copula[20][21]；其中，前面两种方法所构建的树结构形式缺乏一般性，而R-Vine Copula方法完全基于数据的特征来构建自身树结构形式，具有一般性和灵活性[22]。 Diβmanna等也认为 R-Vine Copula方法分析结果的稳健性明显优于C-Vine Copula和D-Vine Copula方法[21]。因此，本文基于R-Vine C-opula模型来系统分析广深港澳四地房价之间的相依结构和传染机制。由于文章篇幅限制，有关R-Vine Copula模型的结构形式和原理可详见相关文献。

四、粤港澳大湾区核心城市房价时变联动性测度分析

（一）粤港澳大湾区核心城市房价指数的选取与说明

本文选取了粤港澳大湾区中的核心城市 （广州、深圳）和中国香港、中国澳门，共4个城市；之所以选择这4个城市，原因在于：一方面，这些城市在粤港澳大湾区中经济较为发达，且其房地产市场规模较大，样本数据相对容易获得；另一方面，这4个城市之间的经贸往来较为紧密，各城市房价之间存在一定的互动关系。基于各城市住宅价格指数的可获得性和代表性，本文选取了东方财富网推出的Choice数据中的各城市房价指数来代表各城市住宅市场价格走势，所有指数均为月度数据。研究时期统一为2011年1月至2018年6月，每个城市各有90个样本数据。本文采用取自然对数形式来计算各城市房价指数的每个时期变化率。各城市房价指数走势及其波动率走势如图1所示。从图1可以看出，广深两市房价走势趋同性较强，而香港和澳门房价走势相似，均呈现出震荡上涨趋势。

图1 粤港澳大湾区核心城市房价指数走势（201101～201806）

表1给出了这4个城市住宅价格指数变化率序列在研究时期内的描述性统计结果。由表1可知：中国香港和澳门城市房价指数收益系列均呈现出轻微左偏尖峰的分布特征，而广州和深圳则呈现出明显的右偏尖峰的分布特征。在正态分布检验上，这4个城市房价收益系列的JB统计值均拒绝原假设，说明这些城市的房价指数均不服从正态分布。从房价指数标准差来看，从大到小依次是深圳>澳门>香港>广州。这表明4个城市中，深圳房价波动最为激烈，广州房价波动率最小。

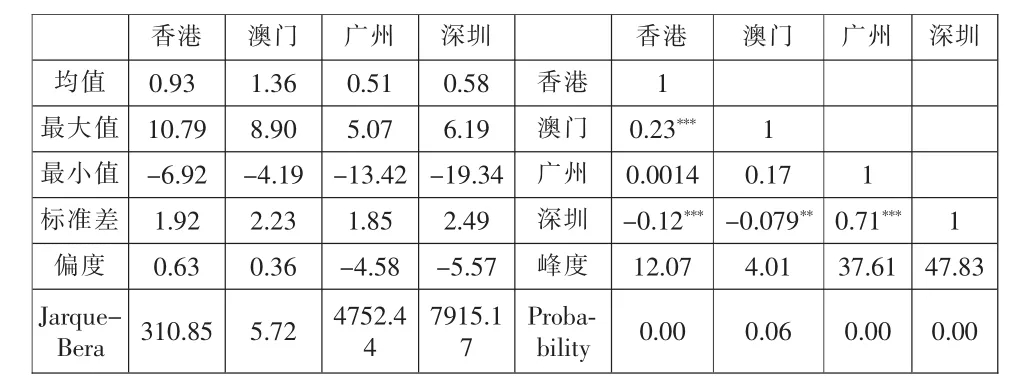
表1 粤港澳大湾区核心城市房价指数收益序列的描述性统计结果

从表1中四城市房价之间的线性相关性来看，广深两市之间的相关性最高，达到0.71，说明两市房价走势较为同步；从这两个城市房价走势来看，两者均从2014年中开始进入下跌周期，但深圳在2015年中就率先开始上涨，而广州则直到2016年中才开始上涨。其次是香港和澳门之间的房价相关性，达到0.23。说明港澳两地楼市走势存在正相关性，走势具有一定趋同性；香港与深圳的房价相关性为-0.12，说明港深两市楼市走势存在相反趋势，与此类似，深澳两市的房价相关性也为-0.079，说明两者同样存在较弱的负相关性。而广州与香港楼市之间的相关性较弱，仅为0.0014；但广州与澳门之间的房价相关性为0.17，说明两市存在一定的正相关性。

（二）边缘分布模型的参数估计结果

结合各城市房价指数，我们运用极大似然估计法对边缘分布函数ARMA(1,1)进行参数估计；此外，为了检验序列概率积分变换后是否服从（0,1）分布，本文引进K-S Z统计值进行检验，结果如表2所示。从表2的估计结果可知，香港和澳门的c0参数分别在1%和5%的置信水平上显著，而广州和深圳的c0参数缺乏统计显著性。广深港澳四城市的c1参数均显著为正，说明这4个城市房价走势均存在明显的自相关，也即房价走势具有明显的惯性特征。与此同时，香港和广州的参数θ1在1%的置信水平上显著，这说明香港和广州的房价波动率具有显著的自相关性，相较于澳门和深圳，这两个城市房价波动更具有持久性。动态相关系数a参数和b参数均显著，且a+b<1，符合DCC模型的参数约束条件，说明DCC模型的建模效果较好；从K-S检验的Z统计值及渐进显著性来看，变换后的序列不服从（0,1）均匀分布，但由于Z值均落在0与1之间，说明变换后的序列适合进行RVine Copula建模分析其相依结构特征。

表2 DCC模型估计结果

（三）粤港澳大湾区核心城市房价时变联动性

图2为广深港澳四地房价在2011年1月～2018年6月的时变联动性走势，表3对4个城市在研究时期内房价之间的联动性进行统计汇总。从图2和表3可看出，这4个城市之间的房价联动性具有时变特征，且各自的走势不尽相同。香港与澳门之间的房价联动性在整个研究时期内呈现出震荡走低的趋势，两市房价联动性最高为0.34（2012年4月），最低联动性为-0.07（2017年3月），联动性的波动率为0.06；广州与香港、广州与澳门的时变联动性走势较为相似，大体上表现出微弱0值上下波动的态势，这说明广州房价与香港和澳门的房价联动性较弱。深圳与香港、深圳与澳门的房价时变联动性均值分别为-0.06、-0.04，这说明在大部分研究时点上，深圳房价走势与香港和澳门的房价走势相背。相比之下，广深两市的房价走势均表现较强的正相关性，其时变联动性均值为0.79；两市房价时变联动性走势在部分时期上走势平稳，但在2013～2016年期间却表现出激烈的大幅波动特征；广深两市房价联动性由2013年4月的0.83开始出现大幅下降，最低降至2013年12月的0.61，然后又大幅上升至2014年7月的最高值0.98；随后又持续回落至2015年7月的0.63的低点，直至2016年初才开始恢复到0.79的平均水平上。显然，这段时期内，广深两市房价走势出现了从背离到趋同的反复过程，这可能与该时期内房地产市场调控政策的变迁有关。我国在2014年开始放松了2013年以来的严厉限购政策，转而实施以“去库存+稳增长”为目标的宽松调整政策，随后从2014年6月起，非一线城市限购陆续取消。在这些调控政策的影响下，广深两市房价开始由之前的横盘整理状态转为上涨态势，从而使得两者的房价走势趋同且联动性不断提升；2015年政府进一步实施更为宽松的调控政策（3月30日五部委将二套房首付比例降至40%、出售房屋营业税免征年限由5年缩短至2年），这使得广深两市房价联袂持续上涨，进而使得两市房价联动性保持在较高水平；进入2016年后，随着热点一线城市房价大幅上涨引发中央政府的警惕，房地产调控政策由宽松进入严厉的紧缩阶段 （以六限为标志：限购、限贷、限售、限价、限土拍、限商改住），由此国内一线城市楼市先后进入冰冻状态，从而导致广深两市房价的联动性由高位回落至正常水平。由此可见，这些核心城市各自房地产调控政策差异及楼市管理体制差异造成了其城市房价联动性走势差异。

图2 广深港澳城市房价时变联动性走势

表3 广深港澳城市房价时变联动统计汇总

五、粤港澳大湾区核心城市房价波动传染效应分析

（一）广深港澳房价相依结构及波动溢出效应分析

本文以广深港澳四地房价为研究对象，所以R-Vine Copula模型的维度d=4，模型在理论上含有2d-1=23=8个不同的RVM矩阵，为了确定最佳的RVM矩阵，本文参考J.Diβmanna等[21]通过最大生成树方法确定最佳RVM的方式；随后采用常用的似然函数值LL最大、AIC和BIC值最小的原则确定从31种备选Copula模型中确定最佳的Copula模型；与此同时，采用R编程实现R-Vine Copula下各边Copula类型的选择和参数估计。R-Vine结构中的第一棵树各边代表无条件相依性，随后树结构中各边均为条件相依性。由于篇幅限制，这里只给出在整个时期内广深港澳城市房价相依结构中第一棵树结构及其相依性估计结果（见图3(a)）②。

图3 广深港澳城市房价相依结构及其因果关系

从图3(a)可看出，广深港澳城市房价相依结构中共出现了3类copula模型：t、F、C90依次分别代表了 student t Copula模型、Frank Copula模型、Rotated Clayton90 degrees Copula模型；其中，t模型适合刻画具有上下厚尾对称的线性相依结构，F模型适合刻画具有上下尾对称的非线性相依结构，C90模型是Clayton Copula模型顺时针旋转90度而形成的，适合存在非对称上下尾的负相依性结构。从图3(a)可知，在整个时期内，广深港澳城市住宅价格之间形成线性链式相依结构和区域聚焦特征：深圳与广州直接相连，广州又与香港相连，而香港与澳门相连。与此同时，各相连城市之间的相依结构和相依性也存在明显差异。广深两市房价之间存在上下尾对称的线性相依结构特征，且相依性较大，为-0.5，说明广深之间存在显著的负向波动溢出效应，也即广深两市房价波动存在此消彼长的关系；广州与香港的房价之间存在上下尾对称的非线性相依结构特征，且相依性为0.10，这说明广州和香港之间存在正向的房价波动溢出效应，也即广州和香港房价波动存在相互促进的关系；香港与澳门之间存在非对称的上下尾相依结构，但两者的相依性水平接近于0，仅为-0.022，说明两者之间房价波动溢出效应较为微弱。总体来看，广州和香港在这4个城市的相依结构中起到了承上启下的桥梁中介作用。总体上看，房市体制差异、经贸往来关系和地理区域相邻程度差异是这些核心城市房价传染与联动存在差异的市场逻辑。

（二）基于相依结构的广深港澳房价波动因果关系分析

上图3(a)只是刻画了广深港澳房价波动之间的相依结构及其相依性，但没有揭示出各城市房价波动之间的因果关系，对此，本文采用格兰杰因果关系检验法来对图3(a)中相互连接的城市房价之间的因果关系进行检验。具体分析思路为：首先对这4个城市房价月度变化率系列进行稳定性检验（ADF单位根检验），结果发现各个城市房价变化率序列均为平稳时间序列；然后采用存在相依性的城市房价变化率序列来构建二元向量自回归模型，根据AIC、SC和HQ值最小准则来确定向量自回归模型的最佳滞后阶数；最后，根据最佳滞后阶数进行格兰杰因果关系检验，具体检验结果③见图3(b)。图3(b)中，箭头方向表示格兰杰因果方向，对应的百分数为置信水平。由检验结果可知，在5%的置信水平上，广深两市互为对方房价波动的单向格兰杰原因，也即说明广深两市房价波动会相互影响，互为因果。与此同时，在5%置信水平上，澳门是香港房价波动的单向格兰杰原因，这说明澳门房价波动会对香港房价波动产生影响，但香港房价波动对澳门房价波动没有明显影响。从上述因果关系结构图来看，广深港澳的房价波动因果关系形成了两个独立的区域 （由广深两市组成的一线城市区域、由港澳组成的特别行政区区域），且两个区域之间不存在明显的因果关系。这种区域内部城市聚焦和区域之间分割的格局主要是由目前大湾区内存在“一个国家、两种制度”的现状所决定的，其背后的市场逻辑依然表现为房地产市场体制差异和城市间经贸往来程度差异。随着港珠澳大桥的正式通车和粤港澳大湾区建设的深入推进，这种房地产市场分割的格局将会逐渐被打破，从而改变这些核心城市房价之间的相依结构和联动性分布格局。

六、结论与建议

本文采用动态条件相关性系数模型（DCC）测度粤港澳大湾区核心城市房价的时变联动性，然后采用R-Vine Copula模型刻画各城市房价的相依结构及其波动传染的市场逻辑。最终结论如下：

第一，广深港澳4个城市房价之间均存在时变联动性，但各自的联动性水平和走势不尽相同。其中，广深两市房价的联动性水平较高（平均联动性为0.79），受到房地产调控政策的影响，两市房价联动性在整个研究时期内呈现出W型走势。香港与澳门的房价平均联动性为0.12，总体上表现出震荡走低的趋势。除此以外，香港与广州、香港与深圳、澳门与广州、澳门与深圳之间的房价联动性较低，趋近于0，且走势平稳，说明港澳地区的房地产市场与广州、深圳的房地产市场之间存在明显的分割现象，双方之间缺乏明显的互动关系。

第二，广深港澳城市房价之间存在链式相依结构。广州和香港在4个城市的相依结构中起到了承上启下的桥梁中介作用。与此同时，相邻城市之间存在非对称的相依性，凸显出非对称的房价传染效应。具体来说，广深两市存在上下尾对称的相依结构，表现出负向波动传染效应；广州与香港之间存在正向房价波动传染效应；香港与澳门之间存在较为微弱的负向波动传染效应。

第三，广深港澳城市房价之间存在非对称的因果关系。广深互为对方房价波动的格兰杰原因，也即说明两市房价互动明显，均对对方房价走势产生明显的助推作用。与此不同，澳门房价波动是香港房价波动的单向格兰杰原因，而香港房价波动对澳门房价波动没有影响。与此同时，广州房价波动与香港房价波动之间不存在因果关系，由此形成了两个分割的房地产市场 （由广深组成的房地产市场和由港澳组成的房地产市场）。

根据上述研究结论，本文认为随着粤港澳大湾区这一国家战略的持续推进，大湾区内各城市之间的经济融合程度将不断提升，会打破目前港澳房地产市场与大湾区内其他城市房地产市场的分割局面，并产生城市房价波动的跨区域相互传染问题，进而严重削弱单个城市的房价调控实施效果。对此，有必要提前建立粤港澳大湾区城市房价波动风险的防控协同机制。除了各地政府独立对管辖范围内的房地产市场进行监管外，还需要通过该协同机制来实现各城市住宅价格波动风险预警、调控政策制定、调控时机和力度等方面信息的协同共享，从而减缓各城市调控政策的相互影响，最终降低房价波动对大湾区科技创新协同进程的抑制作用。

注：

①资料来源：广州日报，http://news.cnr.cn/comment/latest/20170306/t20170306_523639444.shtml。

②对其他估计结果（RVM矩阵、估计参数矩阵和每棵树的相依结构等）感兴趣的读者，可向作者索取。

③为了文章内容的直观，这里不再给出各城市房价之间的格兰杰因果关系检验结果，而在文中以子图的形式表示出来，感兴趣的读者可向作者索取。