基于空间邻近搜索的移动轨迹相对时间模式挖掘方法
张海涛,周 欢,张国楠
(1.南京邮电大学 地理与生物信息学院,南京 210023; 2.南京邮电大学 通信与信息工程学院,南京 210003;3.南京邮电大学 计算机学院、软件学院、网络空间安全学院,南京 210023)(*通信作者电子邮箱zhouhuan8899@qq.com)
0 引言
随着定位技术与移动通信技术的快速发展,基于位置服务(Location Based Service, LBS)的应用产生了大量具有时空特性的移动轨迹数据。挖掘移动轨迹数据从中发现隐含、有用的移动轨迹序列模式[1-2],对于分析、预测人类或动物的相关行为习惯具有重要的参考价值。在生态学中,分析动物的运动路线,可以帮助我们更好地理解它们的行为习惯,当一些动物的运动模式突然改变时,有可能预示即将发生某些地质灾难(例如,地震、海啸等)[3]。在城市智能交通系统中,从大量车辆、行人的运动轨迹数据中发现频繁的移动轨迹序列模式,可以辅助交通规划、交通疏导等[4]。在商业应用领域,从记录人们日常出行行为习惯的运动轨迹数据中,挖掘移动轨迹序列模式并与商业管理系统中客户信息关联,可以实现位置场景感知的商品推荐、目标客户定向广告投送等[5]。
传统的序列模式数据挖掘方法包括:Apriori All[6-8]、频繁模式树(Frequent Pattern tree, FP-tree)[9]、PrefixSpan[10]、SPADE(Sequential PAttern Discovery using Equivalence classes)[11]等,由于在项集和序列模式的挖掘中没有考虑到移动轨迹数据的时空特性,不能直接应用于移动轨迹序列模式的挖掘。目前,出现了一些改进传统序列模式挖掘方法,可以实现移动轨迹序列模式挖掘。典型的方法主要包括:Cao等[12]提出的一种通过查找不同对象之间相似移动轨迹,发现频繁的移动轨迹序列模式的方法;Shaw等[13]提出的一种基于Apriori算法对移动轨迹数据进行频繁模式挖掘的方法;Pasquier 等[14]提出的一种在归属树森林中挖掘频繁模式的方法;Gatuha 等[15]提出的采用局部广度优先搜索的并行频繁模式挖掘算法;Khoshahval等[16]提出的使用关联规则从轨迹数据发现频繁模式的方法。
但是文献[12-16]存在共性问题:移动轨迹序列模式挖掘方法的执行效率太低。分析主要原因为:没有考虑到在实际应用中产生的移动轨迹数据具有时空邻近特性,直接使用所有频繁项集进行排列组合来生成候选移动轨迹序列模式,会造成候选的移动轨迹序列模式的数量急剧增多,大幅增加方法执行的系统资源开销。为此,本文提出一种基于空间邻近搜索的移动轨迹相对时间模式挖掘方法。
1 基本概念
1.1 移动轨迹
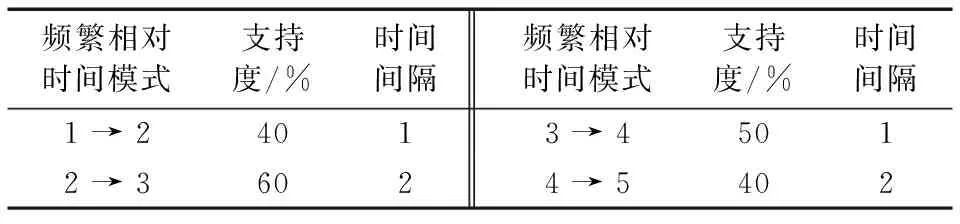
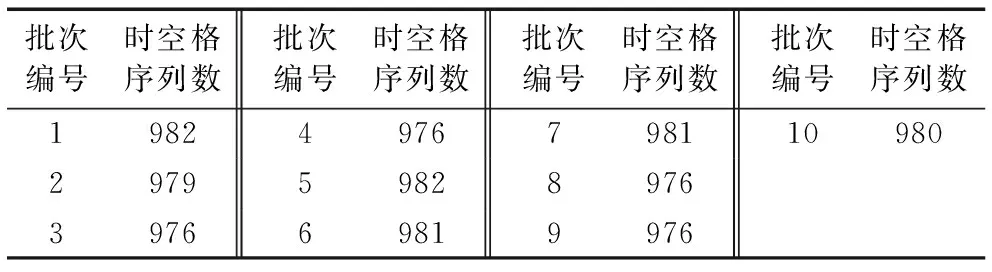
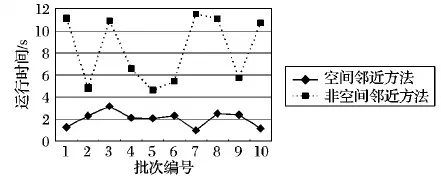
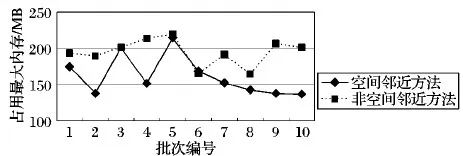
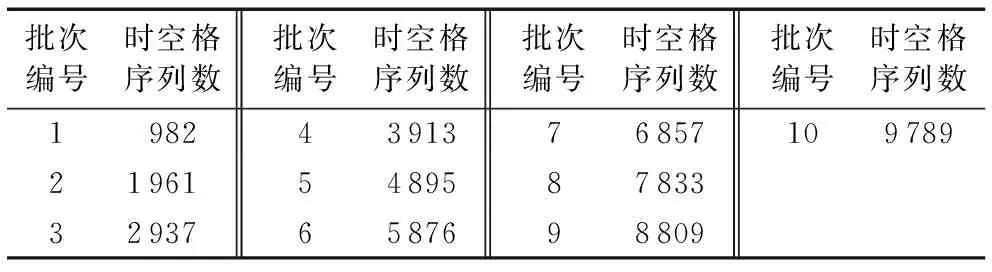
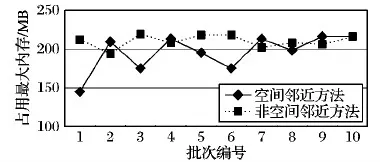
记录用户的连续运动的位置的有序列表,定义为TID=((p1,t1),(p2,t2),…,(pn,tn))(t1 对于一个包含移动轨迹数据集的离散时空域,其中R2表示2维几何空间,pi表示移动轨迹点的空间位置,T表示1维时间,ti表示具体的时间点,其对应的时空格(Space-Time Cell,STC)空间为: STC=(DR2,DT); 其中:DR2是基于时空格的2维几何空间,DT是基于时空格的时间域,每个(Cell(col,row),periodk)称为一个时空格,Cell(col,row)表示时空格的几何空间跨度也称空间格,col、row表示时空格在几何空间平面划分中所处的列号、行号,periodk(s,t)表示时空格的时间跨度也称时间段,j是编号,s、t表示时间域划分中起、止时间,period_count、col_count、row_count分别是根据用户指定的时空分辨率而设定的时段划分数、几何空间划分的列数、行数。 本章定义相关概念,然后设计模式挖掘方法,最后通过实例分析分析方法实现流程。 定义1 时空格序列(Sequence of Space-Time Cells, SeSTC):对于一条移动轨迹TID=((p1,t1),(p2,t2),…,(pn,tn))(t1 TID直接匹配到STC时空格序列定义为: 其中ID表示时空格序列的编号。 依据移动轨迹数据的特性,以及后续数据分析的需要,本文对时空格序列进行如下条件限定: 本文提出的基于空间邻近搜索的移动轨迹相对时间模式挖掘方法包含3个步骤:处理移动轨迹数据、获取长度为2的频繁相对时间模式、对长度为2的频繁相对时间模式进行模式增长,获取长度为3,4,…的频繁相对时间模式,对应的实现算法分别是DataPre()、BasicRelTimePattern()、Pattern-growth()。算法1~3给出了对应的伪代码。 算法1 DataPre()。 输入 移动轨迹数据rawdata; 输出 时空格序列集合SeSTCs,频繁空间网格集合FSCells。 1)rawSeSTCs= ToRawSeSTCs(rawdata); 2)SeSTCs=splitSeSTCs(rawSeSTCs); 3)FSCells=getFrequentCells(SeSTCs); 算法1代码第1)行,读取移动轨迹数据进行时空离散化得到初始时空格序列; 代码第2)行根据空间邻近规则、用户设置的时段邻近阈值,对初始时空格序列进行拆分得到新的时空格序列; 代码第3)行遍历时空格序列得到所有频繁空间网格的集合。 算法2 BasicRelTimePattern()。 输入 时空格序列集合SeSTCs,频繁空间网格集合FSCells; 输出 邻接表集合adjLists,长度为2的频繁相对时间模式IvP2。 1) forFSCellinFSCells 2) listCell=formAdjList(FSCell); 3) adjLists.add(FSCell,listCell); 4) IvP1=FSCell.cellToIvP(); 5) candiIvPs2.add(IvP1.getNextLengthIvps(adjLists)); 6) end for 7) forcandiIvP2incandiIvPs2 8) If (support(SeSTCs,candiIvP2)) 9) IvPs2.add(candiIvp2); 10) end for 算法2代码第1)~6)行,遍历频繁空间网格, 为每个频繁空间网格构建邻接表,并添加到邻接表集合中; 将每个频繁空间网格转变成长度为1的频繁相对时间模式;通过getNextLengthIvPs()方法得到对应的长度为2的候选相对时间模式。代码第7)~10)行,遍历候选相对时间模式,计算在时空格序列集合SeSTCs中的模式支持度,满足支持度阈值的候选相对时间模式添加到长度为2的频繁相对时间模式集合中。 算法3 Pattern-growth()。 输入 长度为n的频繁相对时间模式集合IvPsn,邻接表集合adjLists; 输出 长度为n+1的频繁相对时间模式IvPsn+1。 1) forIvPninIvPsn 2)candiIvPsn+1.add(IvP.getNextLengthIvP(adjLists)); 3) end for 4) forcandiIvPn+1incandiIvPsn+1 5) If(support(SeSTCs,candiIvPn+1)) 6) IvPsn+1.add(candiIvP); 7) end for 算法3代码第1)~3)行,遍历长度为n的频繁相对时间模式,通过getNextLengthIvP()方法获取对应的长度为n+1的候选相对时间模式。代码第4)~7)行,遍历长度为n+1的候选相对时间模式,计算在时空格序列集合SeSTCs中的模式支持度,满足支持度阈值的候选相对时间模式添加到长度为n+1的频繁相对时间模式集合中。 本文方法包含3个步骤,但本文方法与传统方法的本质区别在于模式增长的方式上。本文方法采用空间邻近搜索的方式进行模式增长,而传统方法采用全排列组合的方式进行模式增长, 因此,只分析模式增长算法的时间、空间复杂度。同时,为了简化计算的复杂度分析的对比过程,不考虑模式支持度计算对于算法执行过程的影响,即假定所有的增长模式都满足支持度阈值的限定条件。首先分析两端点情况,然后得到一般情况的复杂度分析对比,结果如下: 1)假定存在n个频繁空间网格,且n个频繁空间网格全部相邻。本文方法与传统方法进行单次模式增长的时间复杂度T(n)都为O(n),空间复杂度S(n)都为O(n), 即在最差的情况下,所有的频繁空间网格全部相邻,本文方法与传统方法的时间复杂度、空间复杂度相同。 2)假定存在n个频繁空间网格,且n个频繁空间网格全部不相邻。本文方法与传统方法进行单次模式增长的时间复杂度T(n)分别为O(1)、O(n),空间复杂度S(n)分别为O(1)、O(n), 即在最优的情况下,所有频繁空间网格全部不相邻,本文方法的时间复杂度、空间复杂度为常数O(1),远小于传统方法的复杂度O(n)。 3)假定存在n个频繁空间网格,其中m(1≤m≤n)个频繁空间网格相邻。本文方法与传统方法进行单次模式增长的时间复杂度T(n)分别为O(m)、O(n),空间复杂度S(n)分别为O(m)、O(n)。 下面结合一个示例,介绍方法执行的基本过程。表1是一个移动轨迹数据库,包含8条移动轨迹。设定频繁空间网格、频繁相对时间模式的最小支持度阈值都为35%,时段邻近阈值为3。 表1 移动轨迹数据库 1)对轨迹数据进行时空离散化得到时空格序列,结果如表2所示。 表2 时空格序列 2)剔除时空格序列中重复时空格,并根据空间格邻近以及用户指定的时段邻近阈值,对时空格序列进行拆分,形成新的时空格序列,结果如表3所示。 表3 新的时空格序列 3)对比表3中的数据与设定的空间网格最小支持度阈值得到频繁空间网格,结果如表4所示。 表4 频繁空间网格 4)根据空间邻近规则组合表4的频繁空间网格。因为设置的时段邻近阈值为3,时间间隔可能为1、2、3,从而得到长度为2的候选相对时间模式。计算候选相对时间模式的支持度,剔除无效的候选相对时间模式,得到长度为2的频繁相对时间模式,结果如表5所示。 表5 长度为2的频繁相对时间模式的支持度和时间间隔 5)表5中的频繁相对时间模式,对照表4,寻找与频繁相对时间模式最后一个空间网格邻近且没有在该频繁相对时间模式中出现过的空间网格添加到该频繁相对时间模式的末尾,并且时间间隔可能为1、2、3,得到长度为3的候选相对时间模式。计算候选相对时间模式支持度,剔除无效的候选相对时间模式,得到长度为3的频繁相对时间模式,结果如表6所示。 表6 长度为3的频繁相对时间模式的支持度和时间间隔 6)表6中的频繁相对时间模式,对照表4,寻找与频繁相对时间模式最后一个空间网格邻近且没有在该频繁相对时间模式中出现过的空间网格添加到频繁相对时间模式的末尾,并且时间间隔可能为1、2、3,得到长度为4的候选相对时间模式。计算候选相对时间模式支持度,没有任何一个候选相对时间模式支持度达到阈值。 本文采用2 612辆出租车上的全球定位系统(Global Positioning System, GPS)轨迹数据作为基础数据,经过时空离散化、图幅网格化,模拟生成时空格序列数据为实验数据[17]。通过在引言部分对传统方法[12-16]的分析,本文方法与传统方法的本质区别在于模式增长时采用了空间邻近搜索的策略。 为突出本文提出的基于空间邻近搜索的相对时间模式挖掘方法性能优势,与传统的方法进行实验对比。性能的对比主要采用两个度量指标:运行时间和占用最大内存。为保证算法性能对比的高效性与有效性,采用本文方法的整体框架,设计了一种只改变其中获取候选相对时间模式的方式,即对频繁空间网格进行排列组合的方式的对比方法。该对比方法一方面代表了传统的典型方法[12-16],另一方面由于采用与本文方法除去模式增长本质不同外的设计框架,可以保证性能对比的公平性。在后续的实验对比部分中,简称本文方法为空间邻近方法,实验对比方法为非空间邻近方法。两种方法执行模式挖掘时设定的频繁空间网格支持度阈值、频繁相对时间模式支持度阈值均分别为3%、0.03%,时段邻近阈值均为3。频繁空间网格支持度阈值、频繁相对时间模式支持度阈值、时段邻近阈值用户可以自行设定,频繁空间网格支持度阈值越大,频繁相对时间模式支持度阈值越大,运行时间越短、占用最大内存越小;时段邻近阈值越大,运行时间越长、占用最大内存越大。本文设定频繁空间网格支持度阈值、频繁相对时间模式支持度阈值分别为3%、0.03%,时段邻近阈值为3,程序运行时间、占用最大内存可以满足对比实验的需要。 实验模拟生成了10个批次的时空格序列数据,基本信息如表7所示。其中,10个批次的数据包含的时空格序列数量基本接近,以对比测试方法性能的稳定性。 表7 10批次时空格序列数据 实验结果如图1、2所示。图1是对比两种方法在运算各个批次数据时所需要的运行时间, 从批次1到批次10,空间邻近方法的运行时间一直小于非空间邻近方法的运行时间。根据图1数据计算,空间邻近方法、非空间邻近方法运行时间的标准差σ分别为689、3 020,表明在运行时间方面,空间邻近方法有更好的稳定性。图2是对比两种方法在运算各个批次数据时占用最大内存。可以看出:运算批次3、5、6的实验数据时,空间邻近方法和非空间邻近方法在占用最大内存性能方面基本相近。对于其他批次数据,空间邻近方法均小于非空间邻近方法。根据图2数据计算,空间邻近方法、非空间邻近方法占用最大内存的标准差σ分别为28、18,表明在占用最大内存方面,两种方法的稳定性差距不大。 图1 10批次数据运行时间对比 图2 10批次数据运行占用最大内存对比 实验结果表明空间邻近方法运行时间更短,占用最大内存更小,在运行时间方面比非空间邻近方法具有更好的稳定性,在占用最大内存方面两者的稳定性差距不大。 为进一步检验方法的可扩展性,本文将表7中的10个批次数据进行增量合并,生成时空格序列数据近似倍增的实验数据,如表8所示。 表8 增量10批次的时空格序列数据 实验结果如图3、4所示。图3是对比两种方法在运算每个批次数据时所需要的运行时间, 可以看出:除批次2数据两种方法的运行时间相同外,空间邻近方法所需要的运行时间均小于非空间邻近方法,而且随着数据量的增大,运行时间的差距越来越大。 图3 增量10批次数据运行时间对比 图4是对比两种方法在运算各个批次数据时占用最大内存, 可以看出:在运行批次2、4、7、8、9、10的数据时,两种方法占用最大内存相近。而在运行批次1、3、5、6的数据时,空间邻近方法占用最大内存均小于非空间邻近方法。 图4 增量10批次数据运行占用最大内存对比 实验结果表明,随着数据量的增大,空间邻近方法所需要的运行时间一直较小,且和非空间邻近方法的差距会越来越大,说明针对增量数据,空间邻近方法在运行时间方面具有更好的可扩展性;空间邻近方法占用最大内存和非空间邻近方法差距不大,但也基本优于非空间邻近方法,说明针对增量数据,空间邻近方法在占用最大内存方面可扩展性稍优于非空间邻近方法。 传统的移动轨迹序列模式挖掘方法以及一些改进方法都存在一个共性问题:没有考虑到在实际应用中产生的移动轨迹数据具有时空邻近特性,直接使用所有频繁项集进行排列组合,生成候选相对时间模式,这会造成候选相对时间模式的数量急剧增加, 因此运行效率低,占用资源多。为此,本文提出一种基于空间邻近搜索的相对时间模式挖掘方法。实验结果表明,本文方法具有运行时间短、占用最大内存小的优点,且方法在运行时间方面具有更好的稳定性和可扩展性,在占用最大内存方面两者的稳定性与可扩展性基本相近。1.2 时空格空间
2 移动轨迹序列模式挖掘方法
2.1 基本定义
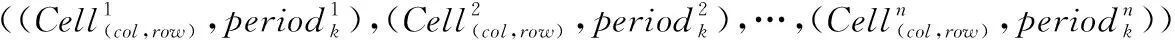
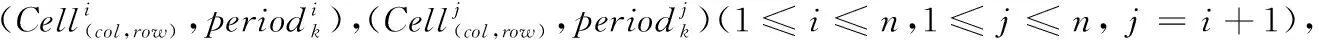
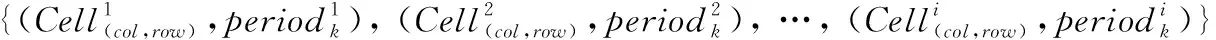
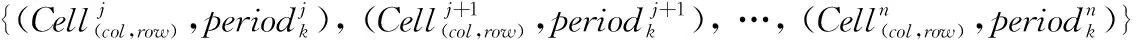
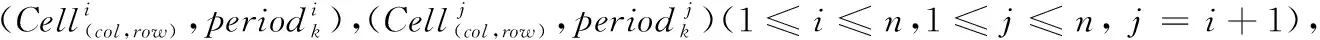
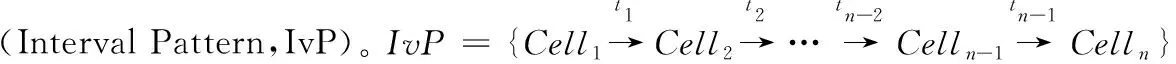



2.2 方法设计
2.3 算法复杂度分析
2.4 实例分析





3 实验结果与分析
3.1 稳定性对比
3.2 可扩展性对比

4 结语

