基于Spark的并行FP-Growth算法优化及实现

顾军华，武君艳，许馨匀，谢志坚，张素琪

(1.河北工业大学 人工智能与数据科学学院,天津 300401； 2.河北省大数据计算重点实验室(河北工业大学), 天津 300401；3.天津商业大学 信息工程学院, 天津 300134)(*通信作者电子邮箱zhangsuqie@163.com)

0 引言

Apriori算法是挖掘频繁项集最有影响和最具有代表性的一种算法，但该算法需要多次扫描数据库，同时产生大量的候选集[1]。基于此，Han等[2]提出了一种不产生候选项集的频繁模式增长(Frequent Pattern-Growth, FP-Growth)算法，通过生成的频繁1-项集列表——F-List来构建一棵频繁模式树(Frequent Pattern-Tree, FP-Tree)，继而挖掘出所有的频繁项集，并且在挖掘过程中只对数据库进行两次扫描，使得挖掘效率以及空间复杂度方面均有很大改进。当数据量较小时，基于FP-Growth算法的改进算法[3]具有一定优势；随着计算规模不断增大，串行FP-Growth算法会因硬件资源的限制遇到内存瓶颈或者失效的问题[4]，基于分布式计算框架的大数据平台成为解决这一问题的一个重要途径。

基于MapReduce计算框架的Hadoop大数据平台，是一种用于分布式并行环境中处理大规模数据的计算模型[5]。继Li等[6]在2008年第一次提出了基于MapReduce的FP-Growth算法——并行FP-Growth (Parallel FP-Growth, PFP)算法之后，不少学者对基于Hadoop的FP-Growth算法进行改进。文献[5,7-8]实现了FP-Growth并行化算法改进，主要针对并行实现方式和构建新的FP-Tree两个方面。与Hadoop平台相比，Spark大数据平台是基于弹性分布式数据集(Resilient Distributed Datasets, RDD)内存的编程框架[9]。2015年，Deng等[10]首次提出了一种基于Spark框架和改进FP-Growth算法的分布式DFP算法，通过在链头表结构中加入一张哈希表以达到快速访问地址的目的，实验证明，与PFP算法相比，DFP算法更高效，集群和数据伸缩性更好; 2016年，方向等[11]提出了在Spark平台上根据不同分组的计算量进行均衡分组思想的改进算法，实验证明优化后的算法要比PFP效率更高; 2016年，Li等[12]通过修改支持度对高置信度数据进行过滤，并将基于Spark的改进FP-Growth算法应用于电信网络中，证明改进算法模式更有效; 2017年，张稳等[13]提出一种基于事务中项间联通权重矩阵的负载平衡并行频繁模式增长算法，实验证明该算法高效并有良好的可扩展性; 2017年，陆可等[14]基于Spark框架，通过对支持度计数和分组过程对FP-Growth算法进行改进，实验证明经优化后的算法在面向大规模数据时要优于传统FP-Growth算法。

综上，基于Hadoop的FP-Growth算法改进主要体现在FP-Tree挖掘方式和并行化实现两个方面；基于Spark的FP-Growth算法改进主要针对优化F-List结构和负载均衡两方面。尽管已经有一些基于Spark的并行化FP-Growth优化算法，但是在优化F-List分组时，考虑了计算量和不同项之间权重对挖掘效率的影响而并未考虑空间复杂度问题，同时也没有考虑数据集进行划分时的时间复杂度问题。本文提出了基于Spark的改进算法——BFPG(Better Frequent Pattern-Growth)算法：首先，通过综合考虑不同分区计算量和FP-Tree规模大小两种因素对F-List分组策略做了优化；然后，对数据集划分策略进行改进，通过减少遍历次数从而降低时间复杂度；最后，运用Spark中丰富的算子对优化算法进行实现。

1 FP-Growth算法描述

FP-Growth是针对Apriori算法效率瓶颈提出的改进算法，用一棵FP-Tree存储数据库中的事务，在不产生候选项集的基础上生成频繁项集。算法通过生成频繁1-项集列表——F-List构建FP-Tree，同时采用递归策略对FP-Tree进行挖掘。在整个挖掘过程中，只对数据集进行两次扫描。FP-Growth算法挖掘频繁项集的过程分为两步：首先构造一棵FP-Tree，然后对FP-Tree递归挖掘找出所有的频繁项集。

1.1 基本概念

设I= {i1,i2,…，im}是一个集合，im称为项，I称为项集。每个事务T是项的集合，T⊆I。

1)支持度计数。项集在事务数据集D的出现次数就是D中包含该项集的个数，称为此项集的支持度计数。

2)支持度。将一个项集的支持度计数与D中事务数之比称为项集的支持度。

3)频繁项集。当一个项集的支持度大于等于某个给定值时，此项集称为频繁项集，这个给定值叫作最小支持度。

4)频繁k-项集。有k项的频繁项集。

5)候选项集。有k个项的集合。

1.2 构建FP-Tree

1)对数据集D进行第一次扫描，计算出所有项的支持度计数，找出满足最小支持度的项，即频繁项，并把这些项按支持度递减排序生成F-List。

2)更新数据集D，将每条事务中的项按照支持度计数从大到小排列，并删除不满足最小支持度的项，只保留频繁项。

3)对数据集D进行第二次扫描，根据D中每条事务出现的频繁项顺序构造一棵FP-Tree。创建树的根节点null，并将每个事务出现的频繁项添加到FP-Tree的一个分支。为了更好地遍历FP-Tree，创建包含头节点的列表，列表中每个元素对应F-List中的频繁项，且每个元素通过一个节点链指向它在FP-Tree中出现的位置。

1.3 FP-Tree挖掘

对FP-Tree进行挖掘时，采用自底向上的递归思想，根据头节点列表中元素的指针指向将所有包含该元素的路径全部找出；然后根据这些路径构造该元素的条件模式基；最后对该条件模式基进行递归挖掘找出包含该元素的所有频繁项集。对列表中所有元素自底向上都执行该操作，最终挖掘出所有频繁项集。

1.4 FP-Growth算法挖掘实例

假设事务数据集D如表1所示，最小支持度设为0.6。算法挖掘流程如下:

1)按照上述1.2节中步骤1)，对D进行第一次扫描，生成的F-List列表为〈(n:5),(m:4),(o:3),(p:3)〉，并按照1.2节中步骤2)更新后的数据库列表如表2所示。

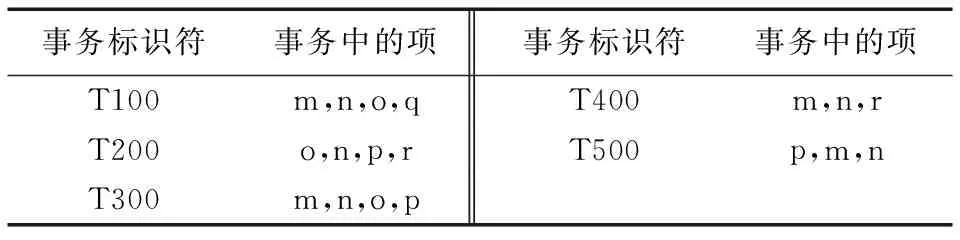
表1 事务数据集D

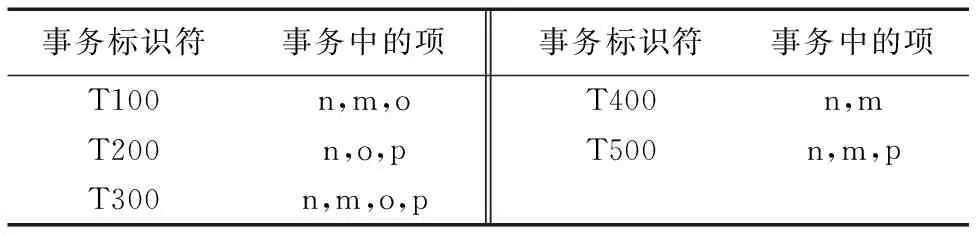
表2 更新后的事务数据集

2)按照1.2节中步骤3)，对数据库进行第二次扫描，生成FP-Tree以及头节点链表，如图1所示。

图1 生成的FP-Tree

3)按照1.2节中的步骤3)，继续对FP-Tree进行递归挖掘得到的频繁项集如表3所示。

表3 递归挖掘得到的所有频繁项集

基于Spark的并行FP-Growth算法思想是将原始数据集划分到不同的分区，然后按照如上述步骤在各个分区构建局部FP-Tree并且分别进行频繁项集的挖掘，最后综合各个分区得到全局频繁项集。

2 基于Spark的FP-Growth算法实现

随着数据集规模的增大，FP-Growth算法构建的FP-Tree横向和纵向维度都会逐渐增大，存储大规模的FP-Tree会出现失败；同时由于挖掘FP-Tree过程中的递归次数增加，造成挖掘效率变得极低[15]。基于Spark的并行FP-Growth算法通过构建局部FP-Tree对各个节点的频繁项集进行挖掘，最后合并得到全局频繁项集。

Hadoop分布式文件系统(Hadoop Distributed File System, HDFS)的作用是存储大数据平台上数据集文件, 并且提供统一的命名空间定位文件。Spark平台将数据抽象为RDD，不仅有很强的容错性和可并行的特点，同时提供了丰富的算子进行不同的操作。

FP-Growth算法在Spark上的并行实现主要分为4个步骤：1)从HDFS上读取原始数据集，对数据集进行更新并且产生F-List；2)对数据集进行划分，按照一定规则将数据集中的每条事务划分到不同的分区中；3)对每个分区按照第1章所介绍的串行FP-Growth算法进行频繁项集的挖掘；4)将步骤3)中的每一个分区中的频繁项集挖掘结果进行合并，得到整个数据集的挖掘结果并将结果输出。算法主要实现过程如图2所示。

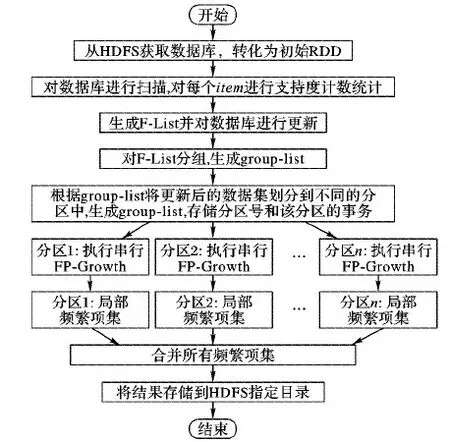
图2 Spark上实现FP-Growth算法流程

从图2可以看出，对F-List进行分组是整个并行挖掘任务的重要环节，直接影响后面步骤中FP-Growth算法挖掘效率；同时，数据集采取何种划分策略也会影响并行FP-Growth算法执行效率。

3 BFPG算法

本文提出一种新的基于Spark的FP-Growth算法——BFPG算法: 首先综合考虑不同分区计算量和FP-Tree规模大小两种因素对F-List分组策略进行优化；然后通过减少遍历次数对数据集划分策略进行改进；最后运用Spark中丰富的算子进行实现。

3.1 F-List分组策略优化

F-List分组是整个并行挖掘的重要环节。由于对频繁项集进行并行挖掘的时间取决于最后一个分区完成的时间，所以在进行分组时应该尽量使每个分区的挖掘时间相等，使每个分区的挖掘任务尽可能均衡，因此F-List的分组策略十分关键。

已有的并行FP-Growth算法中F-List分组策略[16]：首先根据F-List中的元素个数和分组数g求出划分到每个分区的最小元素个数为num，然后对已经按照支持度降序的F-List从后向前遍历，将其中(i%num+1)到(i+1)*num(i:0～g-1)的项划分到第i组。

假设F-List中的元素个数为9，分别用9，8，7，6，5，4，3，2，1(用数字代表支持度的降序排列)表示，分区个数为3。未优化的分组策略示意图如图3所示。

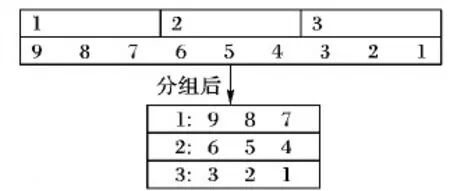
图3 未优化分组结果示意图

根据第1章中介绍，在构建FP-Tree时，从根节点到叶子节点支持度逐渐降低，由于支持度越低时，根据该项构建的条件模式树越高，递归次数越多，相应的挖掘任务负载越大，因而将支持度相对较大的项和支持度相对较小的项划分到不同分区中，会造成不同分区之间的挖掘时间有很大差别，故造成负载不均衡。从图3可以看出，第1组负载最高，第3组负载最低，造成挖掘任务负载不均衡从而影响挖掘效率。

已有的优化算法在分组策略上的改进主要是根据不同分区的计算量，注重时间复杂度。本文增加FP-Tree规模这一参考标准，即考虑各个分区中FP-Tree的横向和纵向维度。通过综合考虑时间复杂度和空间复杂度，得出负载均衡的分组策略，从而更好地对F-List进行分组。具体求出不同分组的计算量非常复杂，但是基于上段的分析，计算量主要体现在不同项所处路径的长度，而这是由该项item在F-List列表中具体位置决定的，据此对分区挖掘频繁项集计算量Calculation可以用式(1)进行估计：

Calculation=Log(L(item,F-List))

(1)

FP-Tree规模是由项在F-List中的位置和该项的支持度计数进行度量。假设项的支持度计数为item_sup，项在F-List中的位置为item_loc。FP-Tree的规模可用式(2)进行估计：

Size=item_sup×(item_loc+1)/2

(2)

式(2)中:item_sup越大，对应的item_loc也越大，即这两个变量有相同的变化趋势，所以可以得出树的规模主要由item_loc决定。在确定了两个度量标准之后，可以将分组策略优化示意图表示出来，如图4所示。假设F-List中元素个数为18，分区数为3，图4中横轴代表项item在F-List列表中的位置，图4(a)中实线和虚线分别代表未优化分组时的计算量和FP-Tree规模大小，优化分组之后如图4(b)所示。

虚线a与经过对称变换的曲线的交点所对应原曲线的x轴坐标，即为优化之后的每个分区中的元素。采用这样的划分可以保证在某一时刻总是将较大计算量和局部FP-Tree规模较大的那个后缀模式项放在计算量和局部FP-Tree较小的那个分区中，保证分区与分区之间的计算量和FP-Tree存储规模大致相同，实现负载均衡。

图4 分组策略优化示意图

仍假设F-List中的元素个数为9，分别用9，8，7，6，5，4，3，2，1(用数字代表支持度的降序排列)表示，分区个数为3。优化后的F-List分组策略示意图如图5所示。

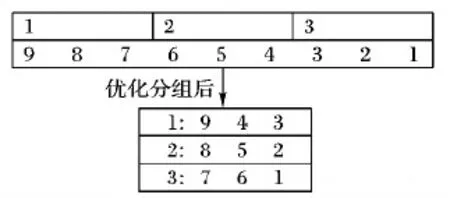
图5 优化分组结果示意图

从图5可以看出，优化分组策略使得剩余频繁项中负载最大的项划分到当前分区中负载最小的分组中，达到不同分区之间的负载均衡。

3.2 数据库划分策略优化

FP-Growth算法的并行挖掘是将数据集划分为一系列分数据集，从而构建一系列局部FP-Tree，最后挖掘所有频繁项集。数据集的划分是要将每条事务划分到不同的分区。划分规则如下：数据集中某条事务Ti划分到不同的分区时，会将Ti从后向前进行遍历，如果项ai对应的分区在遍历ai之前是第一次出现，则将ai以及ai之前的所有项全部写入ai对应的分区中，否则不做任何操作，继续向前遍历。对数据集中每条事务都执行此操作可以将数据集划分到不同的分区中，继而进行并行化频繁项集挖掘，同时也保证了最终挖掘出的频繁项集具有完整性。

在数据集划分过程中，事务中的每一项都进行遍历，所以本文提出在划分数据集之前，构造一个与group-list相同的列表P-List,构造该列表的作用是减少对group-list的遍历次数从而提高数据集划分效率。在对一条事务进行遍历时，为了判断某元素所在分区的分区号是否出现过，需要对group-List进行遍历，如果没有出现过则对事务进行划分，否则继续遍历。若遍历事务的每一项都把该项对应的分区里的所有元素从P-List中删除，只对列表中已有元素执行划分操作，无需再对相同分组的项进行判断。

通过创建P-List，将出现在相同分区的项删除，在对事务进行遍历时就不会遇到相同分区的情况。相比遍历group-list，这一过程能降低时间复杂度。

假设有g个分区，group-list中有t个元素，事务长度为trans_len,则未创建P-List时数据集划分的时间耗费为trans_len*t，加入P-List之后，数据集划分的时间耗费包括三部分：在P-List中遍历相同分区数的元素的时间耗费(g*t)，判断元素的分区数的时间耗费为t以及遍历整条事务的时间耗费trans_len，数据集时间耗费可用式(3)表示:

Time_cons=(g+1)×t+trans_len

(3)

由于在挖掘过程中t和trans_len要比g大得多，所以比较改进前后时间耗费，可以看出创建P-List列表会大幅减少划分数据集的时间耗费，从而降低时间复杂度，提高挖掘效率。

为清晰表达该优化策略，本文对数据库中的一条事务〈Ti: a f c m p〉进行划分举例。优化过程如图6所示。

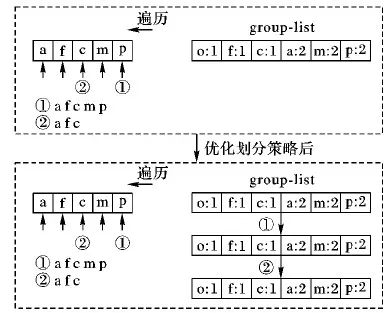
图6 数据库划分优化结果示意图

未创建P-List时，遍历事务每一项都会对group-list进行一次扫描，对事务进行两次划分操作①、②；对划分过程进进行优化后，也对事务进行同样两次划分操作，但是，在每进行一次划分之后都会对P-List进行相同分区的元素进行删除，这样当遍历到事务某一项, 若该项是当前P-List中的元素，则进行划分操作，否则继续向前遍历。

4 实验与结果

为了验证本文所提出的BFPG算法的有效性，实验选取元数据集retail.dat[7]，该数据集取自Frequent ItemSet Mining DataSet Repository[17]，该网站提供的数据集常用于频繁项集研究。对retail.dat数据集扩展事务数生成6个测试数据集，记为{D1,D2,D3,D4,D5,D6}，各数据集的特征统计信息如表4所示。

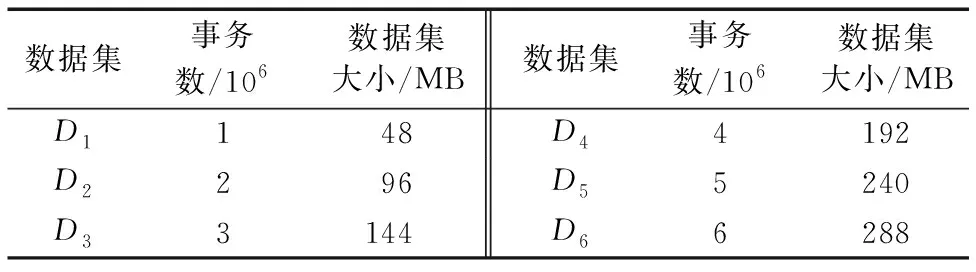
表4 数据集特征信息统计

实验所用Spark集群由5个节点构成：其中1个节点既是主节点也是从节点，其余4个为从节点，每个节点的配置为：CPU核数为4，内存为8 GB，操作系统Centos 6.8，Hadoop版本：hadoop-2.6.2，Spark版本为spark-1.6.1-bin-hadoop2.6.2，JDK版本为JDK 1.7.0_79，Scala版本为Uscala-2.10.5。

1)为验证算法有效性，实验取D1～D6共6个数据集，支持度设为0.05。在集群上分别执行基于Hadoop的PFP算法、基于Spark的并行FP-Growth(FP_Growth based on Spark, SFPG)算法和BFPG算法对数据集进行频繁模式的挖掘，实验结果如图7所示。

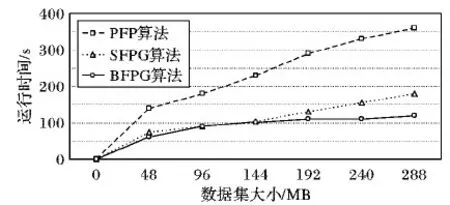
图7 不同算法运行时间对比

从图7可以看出，随着数据量的不断增大，PFP算法的增长趋势要明显大于BFPG和SFPG算法，这是因为基于MapReduce模型框架的算法要频繁地将中间结果存储在内存中以及本身迭代性能不足，从而导致算法执行时间以几乎线性方式增长；随着数据量的不断增大，BFPG算法由于其自身实现负载均衡以及数据库划分策略优化，所以其执行效率要高于SFPG算法。实验结果表明，面对海量数据集，BFPG算法更有利于提高频繁模式挖掘效率。

2)在算法可扩展性的表现性能上进行如下实验：保持支持度不变，集群节点数从1～5递增，分别执行SFPG和BFPG算法对D6数据集进行频繁模式挖掘，实验结果如图8所示。

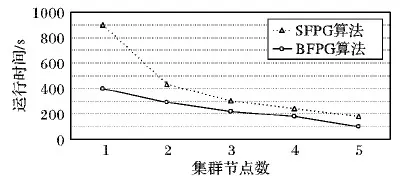
图8 不同节点情况下算法运行时间

从图8可以看出，随着节点数的不断增加，两种算法运行同一数据集的时间不断减少，整个集群处理效率更高，但是BFPG算法相比SFPG算法执行效率更高。实验结果表明，BFPG算法有良好的扩展性。

3)实验通过改变数据集的大小，分析Spark平台在不同节点数目下BFPG算法所需的时间，计算加速比来验证算法的并行性。加速比可以用式(4)表示:

Sp=t/tp

(4)

其中:Sp代表算法加速比，t为使用1个节点时实验执行的时间，tp为使用p个节点时实验执行的时间。

实验取3个数据集D2、D4和D6，分别测试在不同节点数目下的BFPG算法的加速比，实验结果如图9所示。从图9中可以看出，在三个不同数据集下，算法加速比与节点数目的增加近似成正比的关系。实验可以得出，BFPG算法处理数据集具有较好的并行性。

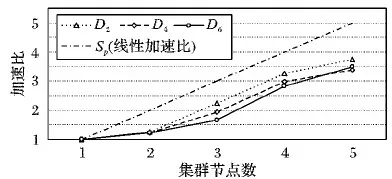
图9 BFPG在不同节点数下的加速比

5 结语

基于Spark的FP-Growth算法主要存在两个问题：F-List分组策略未充分考虑负载均衡问题；数据集划分时遍历次数太多造成时间复杂度很高。基于此，本文提出了一种新的基于Spark的并行FP-Growth算法——BFPG算法，算法首先综合考虑不同分区内FP-Tree规模大小和计算量两方面对F-List 分组策略进行改进，然后通过构造一个新的分组列表P-List对数据集划分策略进行优化，最后对算法进行实现。结果表明，BPFP算法提高了基于Spark的并行FP-Growth算法对频繁项集的挖掘效率；随着集群节点数目增加，算法执行效率不断提高，验证了算法具有良好的扩展性；随着节点数目增加，算法加速比近似呈线性增加，验证了算法具有良好的并行性。