考虑直流侧响应的VSC-MTDC系统协调控制
陈 迅,郭敬梅,曾德辉,张 健,黄 辉
(1. 广东电网有限责任公司电力科学研究院,广东 广州 510080;2. 华南理工大学 电力学院,广东 广州 510640)
0 引言
相比两端直流输电系统,多端直流输电(MTDC)系统能实现多电源送电、多落点受电,为大规模分布式能源并网、大容量远距离输电和城市互联等问题提供了可靠的技术方案[1]。目前,国内南澳岛三端柔性直流工程[2]和舟山五端柔性直流工程[3]已经正式投入运行,张北 ±500 kV柔性直流电网示范工程也正在规划中。
稳定控制问题是基于电压源型换流器的多端直流输电(VSC-MTDC)系统稳定运行的核心问题[4]。直流控制方法可包括主从控制[5]、电压裕度控制[6]、下垂控制[7]及其组合控制[8]等方法。主从控制结构简单,但对高速通信有较大依赖;电压裕度控制无需通信,但电压裕度不易整定[4];下垂控制由于不依赖换流站间的高速通信,可由多个换流站控制电压,系统可靠性高,近年来受到广泛关注[7,9-14]。然而研究表明,采用固定的下垂系数会导致直流电压刚性较差,并且可能引起下垂控制站的满载[9]。对于电压越限问题,文献[10]提出重新设定功率参考值以改变下垂控制截距来稳定直流电压在允许运行范围内。文献[11]将平移下垂曲线和改变下垂曲线斜率相结合,消除直流电压和有功功率静态偏差。但上述文献均不能处理下垂控制站不必要的满载现象。文献[12-14]提出主导换流站的电压下垂系数不应由换流站的额定容量确定,而应自适应地由各换流站的功率裕度确定,并设计了相应的控制方法,但无法解决严苛条件下的电压越限问题。当所连系统的负荷发生变化时,为保持电压稳定及功率平衡,需要相应地修改换流站的功率指令。然而,该指令可能会造成直流功率的满载和直流电压的越限。综上,上述文献无法实现对功率指令下是否发生功率及电压越限的预判,更无法处理两者均越限的工况。
另外,VSC-MTDC系统的稳定性与下垂系数的选取有关。目前分析柔性直流输电系统的稳定性主要采用建立小信号模型的方法[15-18]。文献[15-17]详细介绍了VSC-MTDC小信号模型的建立方法,考虑了系统的各个环节及交、直流侧,但重点分析直流侧时计算复杂;文献[11]采用根轨迹的方法分析了系统的稳定性,但由于其只针对一端换流站进行建模,分析整个系统稳定性时不够准确。为此,需提出一种模型来平衡计算复杂性与精确性。
针对负荷经常波动的VSC-MTDC系统的控制问题,本文提出了一种考虑直流侧响应的协调控制方法。首先,建立了系统的状态空间模型,其可进行系统的稳定性分析,并能反映直流侧的响应过程;然后,针对变化的功率指令,用所提计算模型定量预判该功率指令是否会造成功率过载和/或电压越限,在保证系统稳定性的前提下,采用可同时实现直流网络不平衡功率的合理分配和电压的再调整的参数修正方法;最后,在PSCAD/EMTDC仿真平台上验证了所提方法的有效性。
1 VSC-MTDC系统下垂控制特性分析
本文将以四端环形直流网络为例分析VSC-MTDC系统下垂控制特性,其结构如图1所示。图中VSC1和VSC2采用下垂控制,VSC3和VSC4采用定功率控制。直流输电线路采用π型等效电路,线路电流及对应的方向在图中已标明。
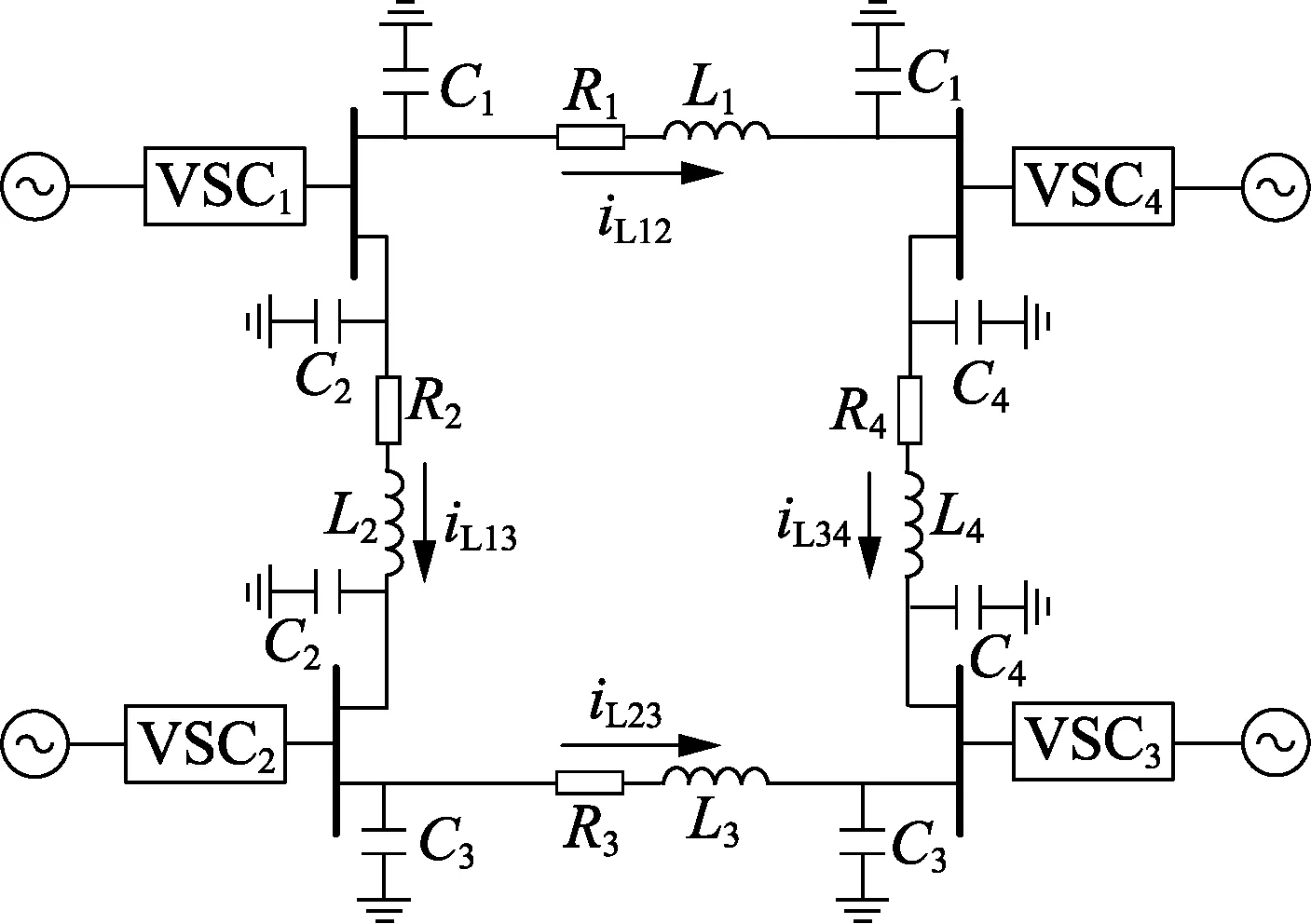
图1 四端VSC-MTDC系统Fig.1 Four-terminal VSC-MTDC system
令Urefi和Ui分别为图1中换流站i的直流电压参考值和测量值。由于Urefi均在1 p.u. 附近,因此令各换流站的参考电压具备全网一致性,即将全网的直流电压参考值仅设置为一个公共直流电压参考值Uref,而实际的直流电压Ui可以各不相同。
图2为下垂控制原理图。图中Prefi和Pi分别为换流站i的有功参考和实际功率,Ki为下垂系数。由图2可知,采用下垂控制方式时有:
Uref-Ui+(Prefi-Pi)/Ki=0
(1)

图2 下垂控制原理图Fig.2 Principle diagram of droop control
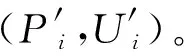
(2)
由式(1)、(2)可得:
(3)
假定m为VSC-MTDC系统下垂控制站的个数,则不平衡功率ΔP可表示为:
(4)
对于直流电网,由不平衡功率导致的电压波动具有全网一致的特性,即ΔU≈ΔUi,因此有:
(5)
由式(5)可见,在保证∑Ki不变的情况下,改变Uref可线性地改变直流电压水平,因此可通过调节Uref来改善系统在不平衡功率下的过电压或低电压问题。
此外,将式(4)代入式(3)可得:
(6)
由式(6)可见,下垂系数Ki决定了分配到各主导换流站的不平衡功率的大小。对于换流站过载问题,则主要通过改变下垂系数来进行调节。
2 考虑直流侧响应的下垂控制算法
2.1 计及有功平衡的状态空间模型
多端直流的电压和功率分配问题都只与系统的有功功率平衡有关,与无功功率无关,而精确地计算系统过电压水平需要了解整个系统的直流响应,因此本文提出了只计及有功功率平衡的状态空间模型。
下文推导过程是基于以下假设:所连的交流电网为强系统,故可忽略PLL的影响;电流内环具有一阶惯性环节的特性,如式(7)所示。
(7)
其中,idi为换流站i的d轴电流;idrefi为相应的d轴电流参考值;Ti为换流站i电流内环d轴的时间常数[19];“*”表示相应变量的标幺值,后同。
(8)
其中,udi为换流站i的d轴电压;Ui和idci分别为换流站i的直流电压和直流电流。
下面介绍各个环节的动态模型。
a. 下垂控制站。
对于下垂控制站i,其控制方程如下:
(9)
其中,ai和bi分别为下垂控制器的比例和积分常数。
引入中间变量yi使得:
(10)
联立式(7)—(10)可得:
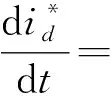
(11)
b. 定有功功率控制器。
对于定有功功率控制器有:
(12)
引入变量zi使得:
(13)
联立式(8)、(12)、(13)可得:
(14)
c. 换流站节点。
对于换流器节点,可将换流器等效电容和直流线路电容等值为Ci,即:
(15)
其中,Ci0为换流器i的子模块电容值;Ni为换流器i的子模块电平数;CLij为线路ij的π型等效电路的等值电容。
换流站直流出口节点处有:
(16)
其中,Ibase、Ubase分别为直流电流、电压基准值;iLij为线路ij的电流。
d. 直流线路。
对于直流线路有:
(17)
式(7)—(17)描述了整个VSC-MTDC系统的动态过程,将其整理为以下形式:
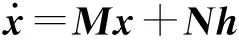
(18)

x0=-inv(M)Nh0
(19)
其中,inv()表示矩阵的求逆运算。综上,只要已知变化前的值h0以及变化后的值h1,不难获取各换流站直流侧的电压、电流以及功率,这是构成本文方法的重要基础。
2.2 系统稳定性分析
对于图1所示的VSC-MTDC系统,有2个下垂系数——K1和K2,其取值的不同可能会影响系统的稳定性。由式(5)和式(6)可知,若∑Ki不变,则各换流站功率增量ΔPi与其下垂系数Ki成正比,且系统电压增量ΔU与Uref呈线性关系,此时系统参数具有良好的控制特性,方便对其进行参数设计。因此,设计K1和K2时增加如下约束:
(20)
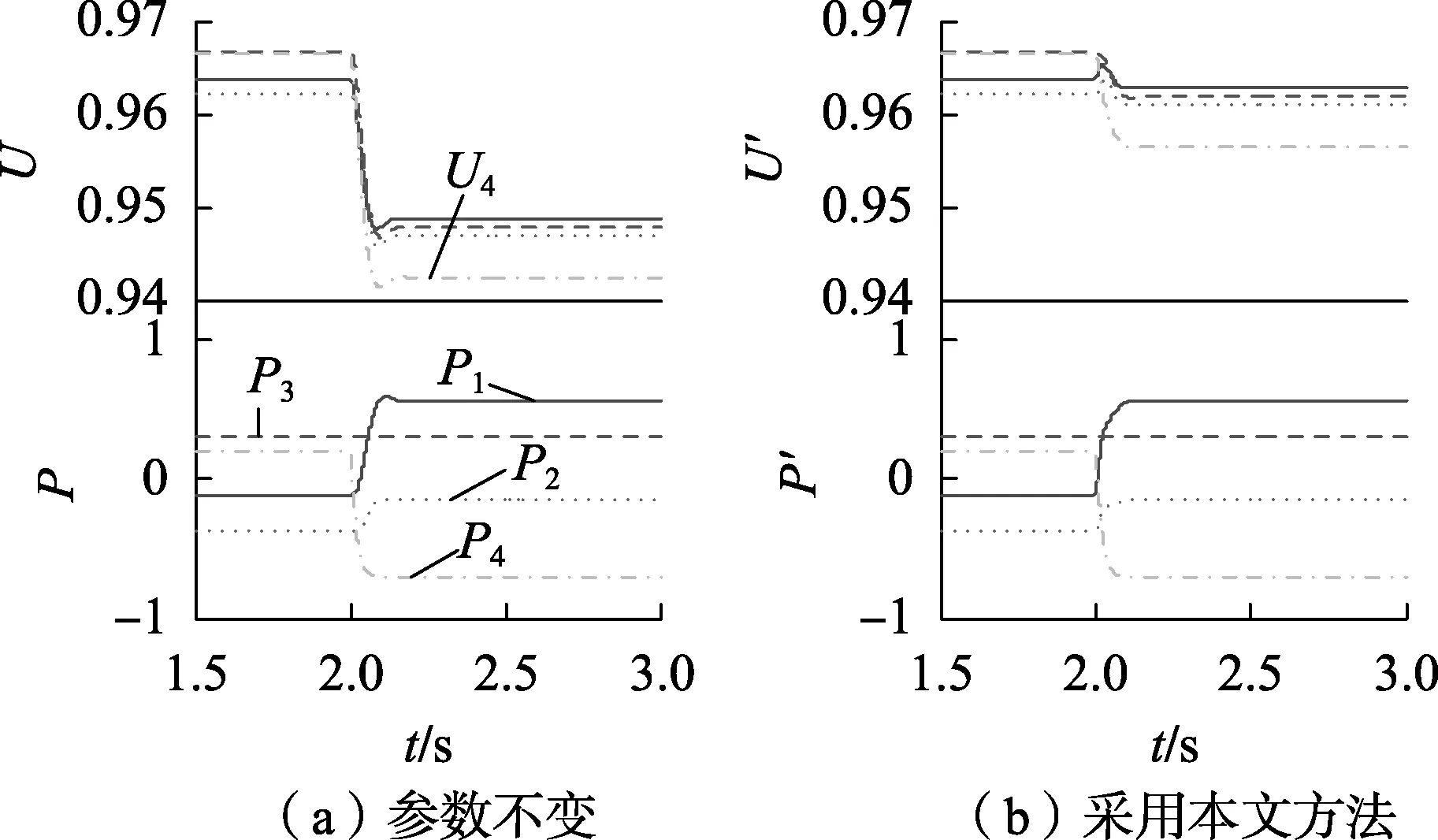
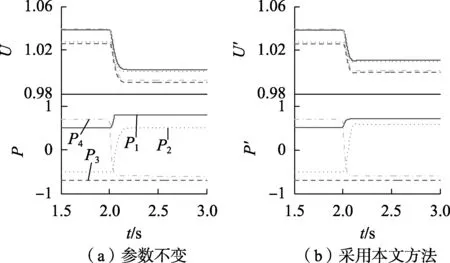
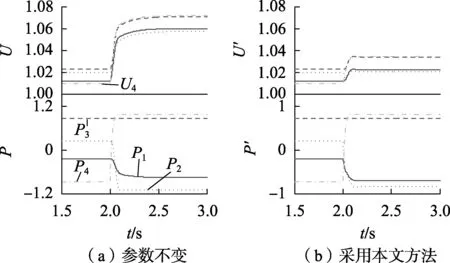
其中,μ为正的定值,且0 本文提出自适应地选取Uref和Ki,同时调节VSC-MTDC系统电压和功率。若以VSC4为例,已知调度发令前、后的2个输入分别为h0=[Uref0,Uref0,Pref1,Pref2,Pref3,Pref4]T、h1=[Uref0,Uref0,Pref1,Pref2,Pref3,Pref4_new]T。其中,h0和h1对应的输出状态分别为状态1和状态2;Uref0为公共电压参考值;Pref4、Pref4_new分别为VSC4在调度发令前、后的指令。并令K1和K2分别为VSC1和VSC2的下垂系数。 考虑较为严重的情况,状态2下有1个下垂控制站过载,且有些换流站电压越限。根据式(5)和式(6)可知:修改电压参考值Uref会影响直流电压水平但不会影响功率分配;功率分配只与下垂系数有关,但修改下垂系数会影响直流电压。基于此,本文先处理功率越限再解决电压越限问题。 2.3.1 功率越限问题 图3 功率越限分析示意图Fig.3 Schematic diagram of power over limit analysis (21) 其中,n为正整数。 2.3.2 电压越限问题 上文已证明,在满足约束式(20)的条件下,改变公共电压参考值Uref可以线性地改变系统电压水平,即可线性地改变系统电压最大值和最小值,这为定量控制VSC-MTDC系统的直流电压提供了便利。正常运行时,设直流侧的电压波动范围为 ±5%(Vmin=0.95 p.u. 和Vmax=1.05 p.u.),由式(18)、(19)计算得到所有换流站各端直流电压后,记录其最大值Umax0和Umin0,那么此时有以下3种情况。 a. 若电压Umax0和Umin0均在允许范围内,则不作调整。 b. 若Umax0>Vmax,则说明系统会出现过电压。为了避免过电压,则需要调低Uref为Urefnew。选取以最低电压限值Vmin为预想新输入,则h2为: h2=[Vmin,Vmin,Pref1,Pref2,Pref3,Pref4_new]T (22) 由h0和h2计算得到电压最大值为Umax1。此时由于改变Uref可以线性地改变Umax,则(Uref0,Umax0)和(Vmin,Umax1)这两点确定了一条直线。如果令最大限值Vmax= 1.05 p.u. 在这条直线上,说明所有直流电压均不会超过最大限值,满足正常运行要求,所求出的Urefnew则为调低的公共电压参考值。同时为了不使Urefnew偏高,将其减去一个直流电压区间宽度,具体可表示为: (Umax1-Umin1) (23) c. 假如Umin0 h3=[Vmax,Vmax,Pref1,Pref2,Pref3,Pref4_new]T (24) 由h0和h3计算得到电压最小值为Umin1。同理,令所有直流电压均不低于Vmin,同时为了不使Urefnew偏低,将其加上一个直流电压区间宽度,具体可表示为: (Umax1-Umin1) (25) 故电压越限后可由式(23)或式(25)计算得到需要调整的公共电压参考值Urefnew。 为验证所提方法的正确性,在PSCAD/EMTDC仿真平台上搭建了如图1所示的四端VSC-MTDC系统,其中换流站采用模块化多电平换流站结构,系统参数如附录中表A1和表A2所示。 本小节将研究当系统发生较大功率变化时系统的动态过程。给定输入如下:h0=[1,1,0.4,-0.6,0.15,0.2]T,h1=[1,1,0.4,-0.6,0.15,0.9]T。即VSC4有功功率由0.2 p.u.上升至0.9 p.u.。 此外,设置初始下垂系数K1=K2=20。利用式(18)、(19)即可快速获得直流侧的动态响应。设在2 s时发生功率阶跃,仿真波形(虚线)与计算波形(实线)的对比如图4所示。图中各变量均为标幺值,后同。由图4可知,当系统有较大不平衡功率时,VSC4的电压U4>1.05 p.u.,即产生了过电压;在发生较大功率变动的情况下,仿真波形和计算波形仍具有较好的一致性,说明了本文所提方法的准确性。 图4 仿真与计算波形对比Fig.4 Comparison between simulative and calculative waveforms 此外,为了便于设计参数,本文增加了约束条件式(20)。为了找到合适的常数μ,令μ在(0,500]内变化。对于每一个μ,通过检测所有典型点(K1,K2)的稳定性,即可获得一条主导极点曲线。主导极点曲线随μ的变化趋势图如附录中图A2所示。由附录中图A2可知,随着μ的增大,主导极点曲线由远及近逐渐靠近虚轴,由近及远逐渐远离实轴。当超过虚轴时,说明在该μ值下有部分点(K1,K2)使得系统不稳定,不满足设计要求。为了使得系统稳定性较强,要求主导极点曲线距离虚轴有一定距离,故本文选择最大主导极点的实部不大于 -15,相应地取μ=60。因此,下文中的计算将均基于约束条件K1+K2=60,而满足该直线上的所有点(K1,K2)均能使得系统稳定。 本文的计算环境为Inter Core i5-5200,CPU 2.2 GHz,RAM 8 GB,MATLAB 2014a。为验证所提控制方法的有效性,本文设计了以下3个算例进行分析(算例中考虑了实际系统的限幅环节)。 3.2.1 算例1:功率不满载、电压越限情形 给定变化前、后的功率指令分别为h0=[0.97,0.97,-0.4,-0.5,0.3,0.2]T、h1=[0.97,0.97,-0.4,-0.5,0.3,-0.7]T。即VSC4的功率指令由0.2 p.u. 翻转至 -0.7 p.u.。设置初始下垂系数K1=45,K2=15,公共电压参考值Uref=0.97 p.u.。 利用式(18)、(19)不难预判上述条件下最低电压U4=0.942 p.u.,因此预判会发生低电压(下垂控制站的功率没有过载),因此只需要调整公共电压参考值Uref即可。通过式(24)、(25)计算得到Urefnew=0.984 p.u.。 上述计算过程耗时为0.018 s,因此具有较快的运算速度。2 s时功率发生阶跃变化,若参数不变则直流电压U和换流站功率P的动态响应如图5(a)所示;若在功率发生变化时采用本文所提方法,其直流响应如图5(b)所示。 图5 算例1仿真结果Fig.5 Simulative results of Case 1 由图5可知,在功率指令发生变化之前,直流电压、功率均在允许运行范围内。VSC4的功率指令在2 s时发生变化,直流电压及功率随之变化,其中变化功率由VSC1和VSC2共同承担且不过载,而直流电压U4超过了最小值。由图5(b)可以看出,调整后的直流电压均在限值以内,且P1、P2值未变说明修改Uref不会影响功率的分配。 3.2.2 算例2:功率满载、电压不越限情形 给定变化前、后的功率指令分别为h0=[1.02,1.02,0.7,-0.6,-0.7,0.7]T、h1=[1.02,1.02,0.7,-0.6,-0.7,-0.6]T。即VSC4的功率指令由0.7 p.u.翻转至-0.6 p.u.。设置初始下垂系数K1=23,K2=37,公共电压参考值Uref=1.02 p.u.。 上述计算过程耗时为0.022 s。2 s时发生阶跃变化,若参数不变则直流动态响应如图6(a)所示;若在功率发生变化时采用本文所提方法,直流动态响应如图6(b)所示。 图6 算例2仿真结果Fig.6 Simulative results of Case 2 由图6可知,当大幅调整了下垂系数之后,功率均在允许范围内,然而仍然不会对直流电压造成过大的影响,其值均在正常范围之内。 3.2.3 算例3:功率满载、电压越限情形 算例3将给出更加严苛的条件,给定变化前、后的功率指令分别为h0=[1.01,1.01,-0.2,0.7,0.8,-0.8]T、h1=[1.01,1.01,-0.2,0.7,0.8,0.9]T。即VSC4的功率指令由 -0.8 p.u. 翻转至0.9 p.u.。设置初始下垂系数K1=10,K2=50,公共电压参考值Uref=1.01 p.u.。 上述计算过程耗时为0.026 s。2 s时发生阶跃变化,若参数不变则直流动态响应如图7(a)所示;若在功率发生变化时采用本文所提方法,其直流动态响应如图7(b)所示。 图7 算例3仿真结果Fig.7 Simulative results of Case 3 由图7可知,在定功率站发生较大功率翻转的情况下,VSC1和VSC2都将接近满载。然而利用本文所提方法仍能找到适当的解,同时调整功率和电压,使得功率和电压均在正常运行范围内。 综上所述,本文所提控制方法能在保证系统稳定性的前提下同时实现VSC-MTDC系统不平衡功率的合理分配和电压再调整,当下垂控制参数发生较大变化时不会对系统造成过大的冲击,且其运算速度在0.01 s数量级,能满足一般控制器的实时性要求。 针对负荷大幅波动的VSC-MTDC系统功率过载和电压越限问题,本文提出一种考虑直流侧响应的VSC-MTDC协调控制方法。该方法针对变化的功率指令,在满足系统稳定性的前提下,用所提计算模型定量预判该功率指令是否会造成功率过载和电压越限,进而调整下垂系数和公共电压参考值,使得功率和电压在正常允许运行范围内。在PSCAD/EMTDC环境下的仿真结果表明,该协调控制策略既可以满足不同运行状态下的运行要求,又可有效维持系统的功率平衡和电压稳定,同时具有较高的运算速度。 附录见本刊网络版(http:∥www.epae.cn)。2.3 协调控制方法设计

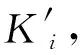

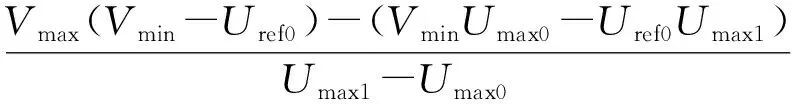
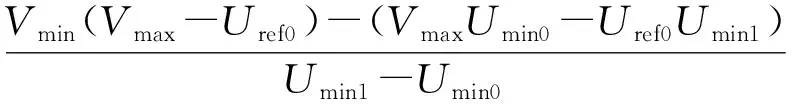
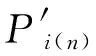
3 算例分析
3.1 状态空间模型验证及稳定性分析

3.2 协调控制方法有效性验证

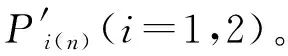
4 结论

