并网大容量调相机对交直流电力系统无功电压灵敏度的影响

黄 华，潘学萍,李 乐，杨 洛，陆进军，颜君凯

(1. 南瑞集团(国网电力科学研究院)有限公司，江苏 南京 211106；2. 国电南瑞科技股份有限公司，江苏 南京 211106；3. 智能电网保护和运行控制国家重点实验室，江苏 南京 211106；4. 河海大学 能源与电气学院，江苏 南京 211100)

0 引言

由于能源分布和经济发展的不平衡，建设以特高压交直流电网为骨干网架、各电压等级电网协调发展的坚强电网是我国电力系统发展的必然趋势[1-2]。

特高压输电系统在带来巨大效益的同时，也带来了运行的复杂性以及一系列的新安全稳定问题，尤其是给特高压直流送、受端近区交流电网电压支撑能力带来了巨大的压力。高压直流输电的传输容量在系统中所占的比例越大，相对而言交流系统就会变得越弱，“强直-弱交”矛盾凸显[3- 4]，直流输电对交流电网电压稳定性的影响也会随着增大。

直流送、受端近区交流电网无功电压状况影响换流站正常运行，同时换流站发生换相失败以及闭锁故障将对交流电网造成严重冲击，系统稳定运行面临较大压力。因此，准确计算交直流互联电力系统的无功电压灵敏度指标，可用于衡量交流子系统与直流子系统的交互作用[5]，识别直流落点近区交流电网的电压薄弱区域，并用于指导在线电压控制[6-7]。

目前关于电力系统无功电压灵敏度的研究已经有了较多的报道[8-11]。反映电压稳定性的灵敏度指标主要包括负荷电压相对于负荷功率的灵敏度dVL/dPL、dVL/dQL，发电机功率相对于负荷功率的灵敏度dQg/dPL、dQg/dQL，以及负荷电压相对于发电机电压的灵敏度dVL/dVg等。文献[12]将灵敏度按照物理意义分为母线灵敏度、支路灵敏度以及发电机灵敏度等。文献[13]基于控制量相对于状态量的灵敏度指标，研究了直流系统控制参数对交直流混合系统运行特性的影响，以及在存在直流系统条件下交流系统控制量对交流系统其他变量的影响。

电力系统无功电压灵敏度的计算建立在潮流方程的基础上，不同之处在于潮流方程的处理、灵敏度指标的定义等。电力系统中既有PQ节点，也有PV节点或者扩展的节点类型[14]。对于PV节点，由于其无功功率约束在潮流方程中不出现，为计算PV节点的无功电压灵敏度，一般的做法是在潮流方程中增广PV节点的无功约束方程[15-16]。然而PV节点的无功功率是待求量，在灵敏度计算中为何可以进行上述处理，现有文献对该问题的讨论还较少。

目前随着新一代大容量调相机在特高压交直流电力系统的推广应用[17-18]，交直流电力系统的无功电压灵敏度将产生较大变化。这是由于大容量调相机不仅具有较强的动态无功支撑能力，也具有较强的稳态无功支撑能力，稳态条件下300 Mvar调相机具备300 Mvar迟相和150～200 Mvar进相的持续运行能力。对于现有配置固定电容器的特高压直流落点，潮流计算中可将补偿节点处理成PQ节点；而配置大容量调相机时，由于调相机较强的无功支撑能力，可将该节点处理成PV节点。

对于配置了大容量调相机的特高压直流落点，潮流计算中节点类型的改变使得无功电压灵敏度计算方法与结果和现有固定电容补偿存在较大差异。本文探讨了调相机较强的稳态无功支撑能力下，直流落点近区交流系统发电机节点的无功电压灵敏度的变化规律，并与现有固定电容补偿下的结果进行了对比。本文结果对精确计算大容量调相机并网交直流电力系统的无功电压灵敏度以及对后续控制策略[19]的施加具有重要作用。

1 交直流电力系统的无功电压灵敏度

特高压直流输送功率波动、受端电网的强弱、换流站电容器组的投切等都可能导致直流换流站母线电压的大幅波动。受端电网的无功支撑能力是提高换流站母线电压稳定裕度的重要手段。而受端电网发电机节点的无功功率相对于换流站母线电压的灵敏度指标，是分析受端电网无功支撑能力的重要依据。

随着大容量调相机的逐步投入，交直流电力系统的无功电压灵敏度计算方法和结果将发生重要变化。分析大容量调相机配置下的无功电压灵敏度，进一步了解其变化规律，对于后续控制策略的修正具有重要的指导作用。

1.1 PQ节点间的无功电压灵敏度

交直流电力系统的潮流方程包括交流节点的功率方程、直流节点的功率方程、换流器方程、直流网络的电压电流方程以及控制方式约束方程(本文中整流侧采用定电流控制，逆变侧采用定电压控制)等，具体见文献[15]。

交流节点的功率方程中包含所有的PQ节点，因此计算PQ节点间的灵敏度时，可直接将潮流方程在运行点按泰勒级数展开，略去高次项，可得：

(1)

其中，Δ表示偏差量；下标a对应交流节点，t对应直流节点；P和Q分别为有功功率和无功功率列向量；Δd1、Δd2为换流器偏差方程列向量，Δd3—Δd5为换流器控制方式约束偏差方程列向量；U和θ分别为节点电压幅值和相位列向量；Vd和Id分别为直流电压和直流电流列向量；kT为换流器的变比列向量；w=cosθd，θd为换流器控制角列向量；φ为换流器功率因数角列向量；雅可比矩阵中的各元素H=∂P/∂θ，N=∂P/∂U，J=∂Q/∂θ，L=∂Q/∂U，A21=∂Pt/∂Vd，A22=∂Pt/∂Id，A41=∂Qt/∂Vd，A42=∂Qt/∂Id，A45=∂Qt/∂φ，C14=∂d1/∂Ut，C24=∂d2/∂Ut，F=∂d/∂X，详见文献[5]。令X表示直流量，Δd表示直流系统方程：

(2)

则式(1)可简写为：

(3)

其中，Jd为交直流混联电力系统的雅可比矩阵。

对式(3)求逆，可得：

(4)

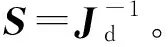
当交流系统中节点j的无功功率Qa(j)变化时(其余节点的有功功率及无功功率均不变化)，可引起系统中其他节点的电压变化，包含直流落点(假设位于节点i)的电压，而灵敏度矩阵S中的对应元素即为无功电压灵敏度S(ij)=ΔUt(i)/ΔQa(j)。

1.2 PV节点和PQ节点间的无功电压灵敏度

实际电力系统中既有PQ节点，也有PV节点[20]。然而潮流方程式(1)中仅包含PQ节点无功功率方程，无法计算PV节点的无功电压灵敏度。文献[15]中指出：要计算PV节点的无功电压灵敏度，可以通过在原潮流方程的基础上增补PV节点无功功率方程的方法。具体如下：首先在交流节点的功率方程中增补该PV节点的无功功率方程，进一步将含增补方程的交直流系统潮流方程在运行点线性化，如式(5)所示。对该式的雅可比矩阵求逆获得灵敏度矩阵，在灵敏度矩阵中该PV节点无功功率ΔQa_PV相对于直流落点电压ΔUt(i)的数值，即ΔUt(i)/ΔQa_PV，即为PV节点与PQ节点间的无功电压灵敏度。

(5)

图1 EPRI 36节点系统接线图Fig.1 Diagram of EPRI 36-bus system

从灵敏度的物理概念来看：可通过改变PV节点的电压设定值计算PV节点无功功率相对直流落点电压的灵敏度，电压设定值的改变将引起系统潮流的变化，从而导致直流落点电压以及PV节点无功功率的改变。根据PV节点的无功功率以及直流落点电压变化量，即可获得PV节点无功相对直流落点电压的灵敏度。

从灵敏度的物理概念可以看出：改变PV节点的电压设定值，也即相当于该PV节点的电压不再恒定，潮流计算中可将其看作PQ节点处理。

1.3 PV节点间的无功电压灵敏度

PV节点间的无功电压灵敏度物理含义为：改变某PV节点的电压设定值，进而引起该PV节点无功功率、系统中PQ节点电压以及其他PV节点电压相位等的改变。然而由于其他PV节点的电压设定值未变化，因此其他PV节点的电压相对于该PV节点的无功功率的灵敏度为0，由此也说明PV节点间的无功电压灵敏度无法计算。

从上述分析可以看出，交直流电力系统间的无功电压灵敏度可根据线性化的潮流方程获得。计算PV节点的无功电压灵敏度时，通过增补PV节点的无功功率方程，相当于潮流计算过程中将该PV节点处理成PQ节点，其本质仍然是计算PQ节点间的无功电压灵敏度。

2 灵敏度结果验证

为验证上述所提灵敏度计算方法的可行性，下面将本文方法的灵敏度结果与摄动法结果相比较。

2.1 算例系统

以图1所示的EPRI 36节点系统为例。该系统共有8台发电机，总发电量为2 741.369 2 MW，总负荷为2 649.8 MW。直流输电系统额定电压为 ±250 kV，额定功率为500 MW，双极运行；交流系统电压等级分别有220 kV与500 kV。系统共分为3个区域，直流输电系统的送端(节点33)与受端(节点34)分别于位于区域2和区域3，整流侧采用定电流控制方式，逆变侧采用定电压控制方式，系统的参数及运行数据见文献[21]。系统中发电机节点3、6、7、8为PV节点，其余节点为PQ节点。

2.2 PQ节点间的无功电压灵敏度

以图1系统为例，基于详细潮流方程，计算换流站近区交流母线29、16、18、13、28、27无功变化引起换流站节点34电压变化的灵敏度。由于上述节点均为PQ节点，故可基于式(1)计算灵敏度。

进一步采用摄动法验证上述灵敏度结果的正确性。具体做法为：将各交流母线的无功功率负荷减小10%，仿真计算节点34电压变化量，据此计算交流系统PQ节点无功相对于节点34电压的灵敏度。

在原系统的基础上分别假设系统中所有节点负荷为原负荷的80%(轻负荷)、原负荷、原负荷的120%(重负荷)3种工况，计算得到无功电压灵敏度结果见表1。

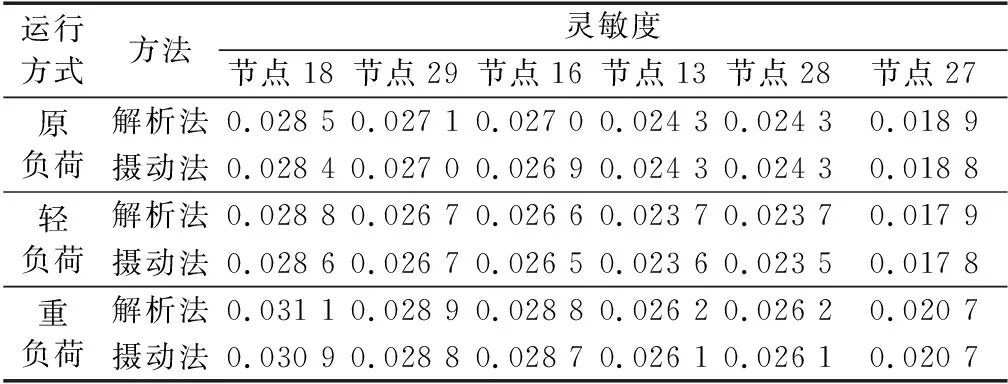
表1 不同运行方式下PQ节点间的无功电压灵敏度Table 1 Reactive power to voltage sensitivities between PQ nodes under different operation conditions

从表1可以得出如下结论。

a. 节点18、29和16的灵敏度较大，节点13、28、27的灵敏度次之，原因在于节点18、29和16距离节点34较近，而节点13、28和27距离节点34稍远。这说明直流落点近区是电压的脆弱区域，应重点关注。

b. 灵敏度解析结果和摄动结果接近，说明了本文所提灵敏度计算方法的可行性。

c. 不同运行方式下各节点无功电压灵敏度接近，说明了本文所提灵敏度指标的鲁棒性。

2.3 PV节点与PQ节点间的无功电压灵敏度

基于图1所示的EPRI 36节点系统，运用式(5)计算PV节点3、6—8无功功率相对于节点34(PQ节点)电压的灵敏度。进一步在PSASP软件中采用摄动法进行验证。摄动时通过改变PV节点电压设定值来改变该节点的无功功率，得到节点34的电压变化情况，结果如表2所示，其中ΔV为标幺值。其中重负荷为额定负荷的1.2倍，轻负荷为额定负荷的80%。

由表2可以得出如下结论。

a. 将PV节点增广到雅可比矩阵中计算得到的灵敏度与摄动法结果较为接近，验证了本文所提PV节点与PQ节点间的灵敏度计算方法的有效性。

b. 节点6距离直流落点节点34距离最近，灵敏度也最大。节点7和8位于直流送端，灵敏度较小。

c. 比较表1和表2可以看出：与节点34距离接近的节点6、13和16中，节点6的灵敏度最大，这是由于节点6为PV节点，具有充足的无功支撑能力。

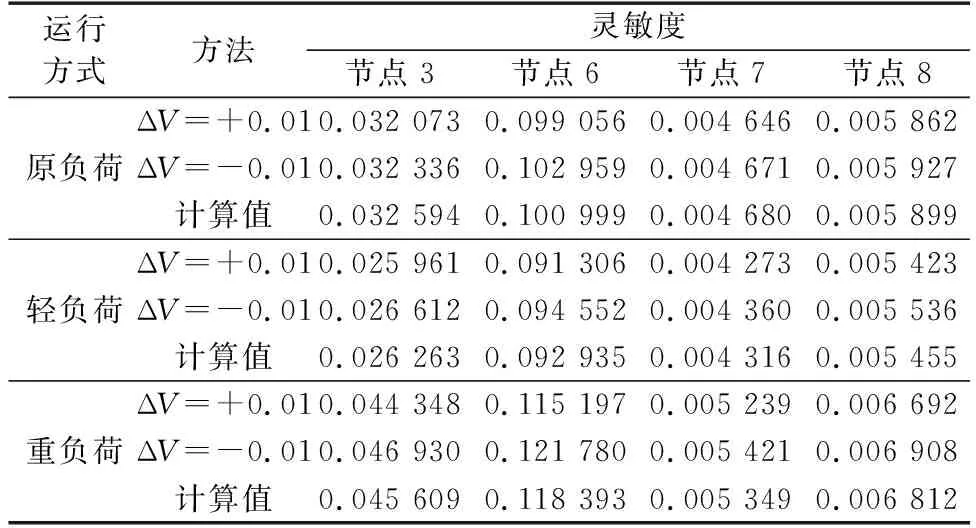
表2 不同运行方式下PV节点无功相对节点34电压灵敏度Table 2 Sensitivities of PV bus reactive power to bus 34 voltage under different operation conditions

3 调相机并网对交直流电力系统无功电压灵敏度的影响

现假设在直流落点节点34装设容量为250 Mvar的调相机，通过升压变压器接入直流落点，设调相机节点为53。为便于比较，假设节点53装设250 Mvar的固定电容进行无功补偿，通过升压变接入节点34。分析装设调相机后，对交直流电力系统无功电压灵敏度(近区交流系统发电机节点无功功率相对于直流落点节点34电压)的影响。

原系统装设固定电容器进行补偿的情况下，灵敏度计算中节点53可以看作PQ节点，此时节点34也为PQ节点；而当采用调相机进行无功补偿时，由于调相机具有较强的无功支撑能力，因此灵敏度计算中将节点53看作PV节点，此时节点34仍然为PQ节点。

上述2种补偿方式下，计算区域2中各发电机节点53、6、4、5无功功率相对于节点34电压的灵敏度，见表3。

表3 不同无功补偿方式下发电机节点无功对节点34电压的灵敏度Table 3 Sensitivities of generator reactive power to bus 34 voltage under different compensation modes

由表3可以得出如下结论。

a. 当采用固定电容补偿(节点53为PQ节点)时，由于节点6为PV节点，具有充足的无功支撑能力，因此其无功电压灵敏度也最大；节点53、4、6为PQ节点，无功支撑能力有限，其中节点53距离节点34距离近，其无功电压灵敏度也较大。

b. 当采用调相机进行无功补偿时，节点53的无功功率对节点34电压的灵敏度最大，节点6次之。这是因为节点53及节点6均为PV节点，有充足的无功支撑能力。但发电机节点4和5均为PQ节点，其无功支撑能力有限，对节点34的无功支撑能力也较弱。

c. 节点53为PV节点或PQ节点时，节点53与节点34的无功电压灵敏度结果相同。这是因为节点53为PV节点时，将其无功功率方程增广到雅可比矩阵中，处理方式与节点53为PQ节点时相同。

可以看出：调相机进行无功补偿方式下，交直流电力系统的无功电压灵敏度与现有固定电容补偿下的结果差异较大。因此在无功优化控制环节需考虑调相机的影响，重新计算无功电压灵敏度。

4 结论

本文基于线性化的交直流电力系统潮流方程，推导了PQ节点与PQ节点之间、PV节点与PQ节点之间的无功电压灵敏度。以EPRI 36节点为例，比较了摄动法及解析法的结果，说明了本文所提无功电压灵敏度的可行性。

本文进一步讨论了大容量调相机补偿方式下，近区交流系统发电机各节点的无功相对于直流落点电压的灵敏度，并与现有固定电容补偿方式下的灵敏度结果进行了对比。指出：近区交流系统发电机为PV节点时，由于有充足的无功支撑能力，其灵敏度较高；发电机为PQ节点时，由于无功功率有限，其灵敏度较低。该结果对后续控制措施的施加具有重要的指导意义。

致 谢

本文得到智能电网保护和运行控制国家重点实验室开放课题(特高压交直流混联电网直流落点近区电压运行特性分析及控制措施研究)的资助，谨此致谢！